001-LA TABLA PERIÓDICA

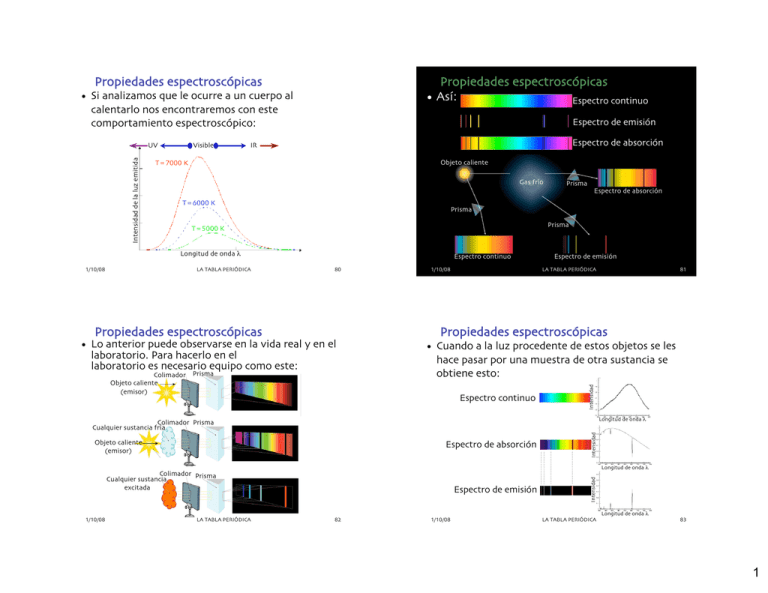
Propiedades espectroscópicas
Propiedades espectroscópicas
• Así:
Espectro continuo
• Si analizamos que le ocurre a un cuerpo al
calentarlo nos encontraremos con este
comportamiento espectroscópico:
Visible
Espectro de absorción
IR
Objeto caliente
T=7000 K
Gas frío
Espectro de absorción
T=6000 K
Prisma
Prisma
T=5000 K
Longitud de onda λ
1/10/08
Prisma
LA TABLA PERIÓDICA
Espectro continuo
80
Propiedades espectroscópicas
1/10/08
Espectro de emisión
LA TABLA PERIÓDICA
81
Propiedades espectroscópicas
• Lo anterior puede observarse en la vida real y en el
laboratorio. Para hacerlo en el
laboratorio es necesario equipo como este:
Colimador Prisma
Objeto caliente
(emisor)
• Cuando a la luz procedente de estos objetos se les
hace pasar por una muestra de otra sustancia se
obtiene esto:
Espectro continuo
Intensidad
Intensidad de la luz emitida
UV
Espectro de emisión
Longitud de onda λ
Objeto caliente
(emisor)
Espectro de absorción
Intensidad
Colimador Prisma
Cualquier sustancia fría
Espectro de emisión
Intensidad
Longitud de onda λ
Colimador Prisma
Cualquier sustancia
excitada
Longitud de onda λ
1/10/08
LA TABLA PERIÓDICA
82
1/10/08
LA TABLA PERIÓDICA
83
1
Propiedades espectroscópicas
• Así en principio cada elemento tiene un
espectro de absorción y de emisión
característico, como se puede ver en esta
liga:
• espectros Hidrógeno
Propiedades espectroscópicas
• En particular los espectros de emisión son parte de
nuestra vida cotidiana, aquí mostramos varios
ejemplos:
Sodio
Helio
Neón
Mercurio
1/10/08
LA TABLA PERIÓDICA
84
85
• Los resultados obtenidos del estudio de los
espectros de líneas de los elementos no podían
explicarse empleando la física clásica.
• Pues si consideramos el modelo del átomo
propuesto por Rutherford, que era muy popular
al principio del siglo XX, al electrón se le
consideraba como si estuviera dando vueltas
alrededor del núcleo.
• De tal manera que la fuerza centrífuga
estuviera balanceada respecto a la atracción
coulómbica.
• Entonces, un átomo así debería de ser capaz de
absorber o emitir cualquier cantidad de energía.
• ¿Pero a qué se debe este fenómeno?
• Lo podemos atribuir a que los átomos que
componen al gas, absorben la luz.
• ¿Y por qué absorben la luz?
• Sabemos que la radiación es causada por la
vibración de las cargas y la rapidez de la
vibración determina la longitud de onda.
• Esto significa que, si solamente ciertas
longitudes de onda pueden ser absorbidas o
emitidas por el átomo, sus electrones vibran
solamente a ciertas frecuencias.
LA TABLA PERIÓDICA
LA TABLA PERIÓDICA
Modelo del átomo y espectroscopía
Propiedades espectroscópicas
1/10/08
1/10/08
86
1/10/08
LA TABLA PERIÓDICA
87
2
Modelo del átomo y espectroscopía
Modelo del átomo y espectroscopía
• De manera que el cambio en su energía
meramente alteraría el radio de la órbita.
• Pero, se sabía que los gases absorbían o
emitían energía en paquetes, es decir estaba
cuantizada.
• En tanto que la luz que se producía por medio
de un objeto caliente (foco), era continua.
• En el año de 1900, Max Planck demuestra
que los átomos de un sólido caliente, tienen
energías que son un múltiplo de una cantidad
fija.
• A esta cantidad de energía le llamó quantum
o paquete de energía.
• Así, los físicos de la época se vieron forzados a
considerar desechar por completo este modelo
(a pesar de estar tan bien sostenido por la
evidencia experimental).
• O hacerle algunas modificaciones difíciles de
digerir.
• Es claro que, sería estúpido proponer que el
átomo pudiera contener cualquier energía (tal
como lo dicta el modelo planetario)
• Y a pesar de ello absorber o emitir energía en
cantidades especiales y medidas.
1/10/08
LA TABLA PERIÓDICA
88
El modelo de Bohr
• ¿Pero entonces como es un átomo?
• Pues la alternativa era postular que los electrones
en el átomo podían tener solamente ciertos
valores de energía.
• Esto implicaba automáticamente, que el átomo
podría absorber o emitir únicamente ciertas
energías.
• Lo que es claro, es que al principio del siglo XX,
este era un verdadero rompecabezas para los
científicos.
• Una teoría o un modelo raramente se abandona
por completo, a menos que no haya alternativa.
• De hecho el modelo planetario no se abandonará
sino hasta que finalmente se desarrolla el modelo
cuántico.
1/10/08
LA TABLA PERIÓDICA
90
1/10/08
LA TABLA PERIÓDICA
89
El modelo de Bohr
• Afortunadamente, (Niels Bohr) un
físico danés, sugiere un cambio al
modelo muy radical.
• Este es el más simple y sensato de los
modelos basado en el de Rutherford.
• Lo radical del modelo, reside en que Bohr
propone que para explicar las líneas espectrales, los
electrones deben seguir una regla medio mafufa.
• Esta regla es que sólo pueden estar en ciertas
órbitas especiales y todas las otras órbitas están
prohibidas.
• Por lo tanto, los electrones pueden saltar de una
órbita a otra y al hacerlo vibran.
• Consecuentemente producen radiación.
1/10/08
LA TABLA PERIÓDICA
91
3
El modelo de Bohr
• Entonces, Bohr descubrió que se podía explicar
cuantitativamente el espectro del hidrógeno si se
consideraba que en el átomo los electrones se
movían únicamente en aquellas órbitas especiales
donde el momento angular del electrón era un
múltiplo de h / 2π.
• Es decir que la energía del electrón estaba
cuantizada.
• Esta propuesta tan arbitraria y mafufa para su
tiempo, es aceptable en parte, por que consigue
salvar el modelo planetario al menos por un tiempo.
• Y la evidencia experimental de la estructura en
capas de los electrones puede verse en los espectros
de líneas.
1/10/08
LA TABLA PERIÓDICA
92
El modelo de Bohr
1/10/08
LA TABLA PERIÓDICA
• Así, en el caso del átomo de hidrógeno, la energía
de cada uno de los niveles cuánticos se puede
obtener usando la siguiente ecuación:
E=!
k Z2
n2
• Y la diferencia de energía entre dos niveles
cualquiera del átomo en cuestión usando esta:
#1
1&
E2 ! E1 = h " = h Z %% 2 ! 2 ((
$ n1 n2 '
2
1/10/08
LA TABLA PERIÓDICA
93
El modelo de Bohr
• De esta manera, este modelo puede racionalizar el
comportamiento químico de los elementos, al
arreglar a los electrones en capas.
• Es decir, al cuantizar las energías de los electrones
en capas discretas (llamadas K, L, M, N, O, etc.),
se pueden explicar las propiedades químicas de los
elementos.
• Esta teoría además predice el número de
electrones en cada una de las capas así:
# de electrones = 2n
El modelo de Bohr
2
94
• En esta tabla se muestran las ocupaciones
de cada capa:
Capa
K
L
M
N
O
n
1
2
3
4
5
2n2
2
8
18
32
50
1/10/08
LA TABLA PERIÓDICA
95
4
El modelo de Bohr
El modelo de Bohr
• Y los niveles energéticos permitidos o estados
energéticos de un átomo (usando terminología
moderna) serán:
• De esta manera tenemos que cuando un átomo
se encuentra en su estado basal y lo excitamos
usando un haz de luz o calor, solamente ciertas
de las longitudes de onda tendrán la energía
suficiente para hacer que el electrón pueda
pasar a otra órbita y serán esas longitudes (o
frecuencias o energías) las que se absorberán .
• Y de la misma manera, cuando dejamos de
excitarlo, los electrones que se pasaron a una
órbita de mayor energía al regresar a su órbita
original emitirán energía.
Momento angular de los estados
espectroscópicos del átomo de hidrógeno
96
El modelo de Bohr
97
• Transiciones del hidrógeno (absorción):
En n
∞
0
1
1230
98
1/10/08
Ultravioleta
LA TABLA PERIÓDICA
Visible
Energía (kJ/mol
(kJ/mol))
−1312.0
0
184
6
5
4
3
2
1167
Capa M, n=3,
n=3, r=4.761
r=4.761 Å
Capa N, n=4,
n=4, r=8.464
r=8.464 Å
Capa O, n=5,
n=5, r=13.225
r=13.225 Å
−36.4
−52.3
−82.0
−145.6
−328.0
246
Núcleo
Capa K, n=1,
n=1, r=0.529
r=0.529 Å
Capa L, n=2,
n=2, r=2.116
r=2.116 Å
LA TABLA PERIÓDICA
LA TABLA PERIÓDICA
El modelo de Bohr
• Órbitas de Bohr del hidrógeno
1/10/08
1/10/08
276
LA TABLA PERIÓDICA
293
1/10/08
p= n ( h / 2π), n es un entero
1 (h / 2π)
2 (h / 2π)
2 (h / 2π)
3 (h / 2π)
3 (h / 2π)
3 (h / 2π)
984
Estado
1s
2s
2p
3s
3p
3d
−1312
99
5
El modelo de Bohr
El modelo de Bohr
• Aquí vale la pena indicar que el átomo de
hidrógeno (y por cierto todos los demás
también), absorben y emiten radiación a otras
longitudes de onda además de las del visible.
• Transiciones del hidrógeno (emisión):
En n
∞
0
1/10/08
1
Ultravioleta
El Hidrógeno se ioniza con energías superiores a 13.6 eV
Lyman Balmer Paschen
Energía (eV
(eV)
Visible
Energía (kJ/mol
(kJ/mol))
184
293
276
984
1230
−1312.0
246
0
6
5
4
3
2
1167
−36.4
−52.3
−82.0
−145.6
−328.0
−1312
LA TABLA PERIÓDICA
100
Bracket
13.6 eV/ molécula
1313 kJ/mol
Series
1/10/08
LA TABLA PERIÓDICA
El modelo de Bohr
El modelo de Bohr
• Es interesante comentar que la propuesta de
Bohr le abre el camino a la mecánica cuántica,
independientemente del hecho de que es
incorrecta casi en todos sus detalles.
• Particularmente, porque el modelo no nos da
ninguna pista del origen de el enlace químico.
• Además no da ninguna base para entender por
que ocurre la cuantización de la energía del
electrón.
• Ni tampoco explica la razón por la cual un
electrón no irradia energía al estar en
movimiento.
• A pesar de este funesto historial, el coraje de
reconocer la necesidad de una desviación de la
física clásica, le ganó a Bohr un lugar en la
historia.
• Todavía hoy, a los estados permitidos, se
conocen como estados estacionarios, tal como
los bautizó Bohr.
• A estos estados estacionarios, se les caracteriza
por medio del uso de los números cuánticos.
• Los cuales explican el patrón característico del
átomo de hidrógeno.
1/10/08
LA TABLA PERIÓDICA
102
1/10/08
LA TABLA PERIÓDICA
101
103
6
¿Partículas u ondas?
¿Partículas u ondas?
• Hasta este momento hemos hablado de los
electrones y de las otras partículas subatómicas
como si fueran pedacitos de materia duros como
bolas de billar (¡tienen masa!).
• Son diferentes a las bolas de billar en que tienen
niveles energéticos claramente cuantizados.
• Estos niveles, pueden medirse de manera muy
precisa, usando los espectros de emisión y
absorción de los elementos.
• Sin embargo estas las partículas subatómicas, a
menudo tienen un comportamiento que no se
puede explicar con este modelo.
LA TABLA PERIÓDICA
104
106
E le
c
tro
ne
s
E
d e le c
sp tro
ed n
id e s
os
• Por otro lado al mismo tiempo se ha demostrado
experimentalmente con un fototubo:
– Que la energía de los electrones emitidos es
independiente de la intensidad del haz
incidente
ia l
ter
e
M a n s ib l
o se
fo t á to d o
c
LA TABLA PERIÓDICA
105
¿Partículas u ondas?
• Así, cuando la luz incide en algunas superficies
metálicas, se produce una corriente de electrones.
• A este fenómeno se le conoce con el nombre de
efecto fotoeléctrico.
Analizador de
• Así, algunos metales Luz
energía
energía
electrónica
m
on
(los alcalinos) pueden
oc
ro
emitir electrones si la
m
át
ic
luz incidente es visible,
a
en cambio otros solo
emiten electrones
con luz ultravioleta.
Metal
• Es decir, para cada
metal hay una frecuencia umbral de la luz, por
debajo de la cual no se produce la corriente de
electrones.
1/10/08
LA TABLA PERIÓDICA
Electrodo
colector
ánodo
Corriente (A)
¿Partículas u ondas?
1/10/08
Radi
aci ó n
1/10/08
• De forma similar, la radiación electromagnética,
tradicionalmente la hemos percibido simplemente
como un fenómeno ondulatorio.
• Sin embargo al estudiarla más, tiene asociadas
ciertas propiedades que el modelo ondulatorio no
puede explicar.
• De hecho estas propiedades se pueden asociar al
comportamiento de las partículas.
• Así, decimos que la radiación electromagnética
tiene momento efectivo y que además también
está cuantizada en paquetes llamados fotones.
Incremento de la
intensidad de la
radiación
radiación
Voltaje
umbral
Voltaje opuesto (V)
1/10/08
Corriente
eléctrica
eléctrica
LA TABLA PERIÓDICA
107
7
¿Partículas u ondas?
¿Partículas u ondas?
– Que el número de electrones emitidos por
unidad de tiempo es proporcional a la
intensidad de la radiación incidente.
– Y que la frecuencia umbral ν0 depende del
material
Energía
eV)
Energía cinética máxima (eV)
Corriente (A)
Frecuencia de la luz incidente
Voltaje
umbral
h =
∆E
∆ν
= 4.1 ×10−15eV ⋅ s
∆E = 1.25eV
∆ν = 3 ×1014
Energía
Energía cinética máxima
– Que la energía de los electrones emitidos es
proporcional a la frecuencia de la radiación
incidente.
La pendiente
de los dos
metales
es la misma
y vale h
ν0 de A
Frecuencia de la radiación
radiación (Hz
(Hz x 1014)
Voltaje opuesto (V)
1/10/08
LA TABLA PERIÓDICA
108
¿Partículas u ondas?
LA TABLA PERIÓDICA
Frecuencia de la radiación
radiación
LA TABLA PERIÓDICA
109
¿Partículas u ondas?
• Este fenómeno, no puede explicarse empleando la
teoría electromagnética clásica pues según esta, la
energía de los electrones debe variar
con la intensidad y además ser
independiente de la frecuencia.
• En 1905, Albert Einstein, demuestra
que se podían resolver estas dificultades
si se aplicaban los postulados de Plank
a este fenómeno.
• Para ello, sugiere que en vez de pensar en la luz
incidente como un fenómeno ondulatorio, debe
considerarsele como una corriente de corpúsculos a
los que llamó fotones.
• Cada uno de estos fotones tiene una energía
determinada que depende de su frecuencia.
1/10/08
1/10/08
ν0 de B
110
• La cantidad de energía de cada fotón está dada
según Einstein por esta expresión:
E fotón = h!
• Cuando los fotones golpean la superficie metálica
estos, pueden ceder su energía a un electrón del
metal.
El potasio necesita al menos 2.0 eV para que se produzca una corriente
• Parte de esta energía la emplea para arrancarlo
de la superficie del metal dándole energía
cinética. Si la frecuencia es inferior a la umbral, el
efecto no se produce.
1/10/08
LA TABLA PERIÓDICA
111
8
¿Partículas u ondas?
¿Partículas u ondas?
• Ahora bien, matemáticamente, ya sea que
consideremos que los electrones (o la luz) como
partículas o como ondas, depende esencialmente
de la observación que pretendemos describir.
• Así, algunas veces una representación será más útil
que la otra, en tanto que en otras ocurrirá lo
opuesto.
• Conviene recordar entonces, que cualquiera que
sea el modelo matemático empleado, el resultado
es una descripción de las propiedades y no de la
naturaleza de los electrones o la luz.
1/10/08
LA TABLA PERIÓDICA
112
¿Partículas u ondas?
• Considerando que es posible pesar a los electrones,
lo cual es tradicionalmente una propiedad de las
partículas.
• Resulta muy desconcertante saber que los
electrones también pueden hacer cosas (como por
ejemplo difractarse) de manera muy similar a la
radiación visible o a los Rayos X.
• Esta es una propiedad que típicamente se percibe
asociada con el comportamiento de las ondas.
• Esto desde el punto de vista de la mecánica clásica,
es claramente una contradicción.
1/10/08
LA TABLA PERIÓDICA
113
¿Partículas u ondas?
• Esta dualidad partícula-onda de las propiedades de
los electrones fue expresada por Louis de Broglie.
• De Broglie, postula que la materia
posee características de onda y de
partícula al mismo tiempo.
• Y expresa esta dualidad en una
ecuación que ya es muy famosa
y se considera que tiene gran
profundidad.
• En esta la longitud de onda se expresa como una
h
función de la masa y de
!=
la velocidad de la partícula.
• Esto nos sugiere, que las observaciones de
comportamiento ondulatorio o de partícula,
simplemente se relacionan a diferentes atributos
de la materia o de la luz.
• Evidentemente, esto es una idea que genera
mucha confusión.
• Para los humanos, todos los días, la experiencia
nos sugiere que las cosas son ya sea partículas o
bien ondas, nunca ambas.
• ¡Una pelota es una partícula y el sonido es una
onda¡
• En la práctica por tanto, la dualidad partículaonda es significativa únicamente para entidades
muy, muy pequeñas.
1/10/08
1/10/08
mv
LA TABLA PERIÓDICA
114
LA TABLA PERIÓDICA
115
9
¿Partículas u ondas?
¿Partículas u ondas?
• El obstáculo que se nos presenta para entender su
naturaleza se debe a que es difícil relacionar
nuestra experiencia cotidiana con la luz y la
materia, con la aparente naturaleza conflictiva de
las partículas que son tan pequeñas.
• Así, parece ridículo sugerir que la materia que
manipulamos cotidianamente puede tener
propiedades ondulatorias, pero no lo es.
• El problema descansa en la magnitud de la
longitud de onda.
• Para cualquier objeto visible, el tamaño de la
longitud de onda es tan pequeño que no puede
percibirse.
1/10/08
LA TABLA PERIÓDICA
116
¿Partículas u ondas?
• Esto ¡es muy pequeño!
1/10/08
LA TABLA PERIÓDICA
117
• Si en el modelo de Bohr, los electrones dan vueltas
alrededor del núcleo en órbitas cuantizadas, el
modelo cuántico ya no lo considera así. Orbital
electrones
núcleo
electrones
h
6.63 " 10 !34
#=
=
$ 1.6 " 10 !6
!30
mv 9.10939 " 10 % 45
núcleo
Órbita estacionaria
Rutherford
Bohr
Schrödinger
• Antes de discutir este modelo, debemos considerar
que, las dos de las piezas de información más
importantes que debemos conocer acerca de un
objeto cualquiera son:
– la posición por una parte y
– la velocidad (o mas bien el momento) por otra.
• Pues resulta que, no es posible determinar con
precisión la posición y el momento de un electrón
al mismo tiempo.
• La cual es una longitud de onda mucho más
observable experimentalmente.
LA TABLA PERIÓDICA
h
6.63 " 10 !34
#=
=
$ 9.81 " 10 !35
mv
0.15 % 45
De órbitas de Bohr a orbitales de Schrödinger
• Por otro lado, un electrón que se moviera a la
misma velocidad, pero cuya masa en estado
estacionario es de 9.10939 x 10-30 kg tendría una
longitud de onda asociada de:
1/10/08
• De esta manera, es posible concluir que longitud
de onda efectiva de una partícula es importante
únicamente cuando la partícula es muy pero muy
pequeña.
• Consideremos una pelota de baseball, cuya masa
es de 150 g y que se mueve a 160 km/h (45 m/s).
• Al sustituir esto en la ecuación de de Broglie:
118
1/10/08
LA TABLA PERIÓDICA
119
10