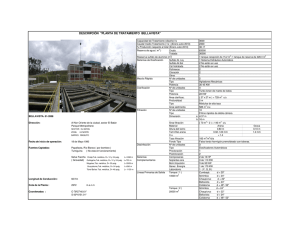
Ejercicios Resueltosy propuestos de Ecuacion de Continuidad.

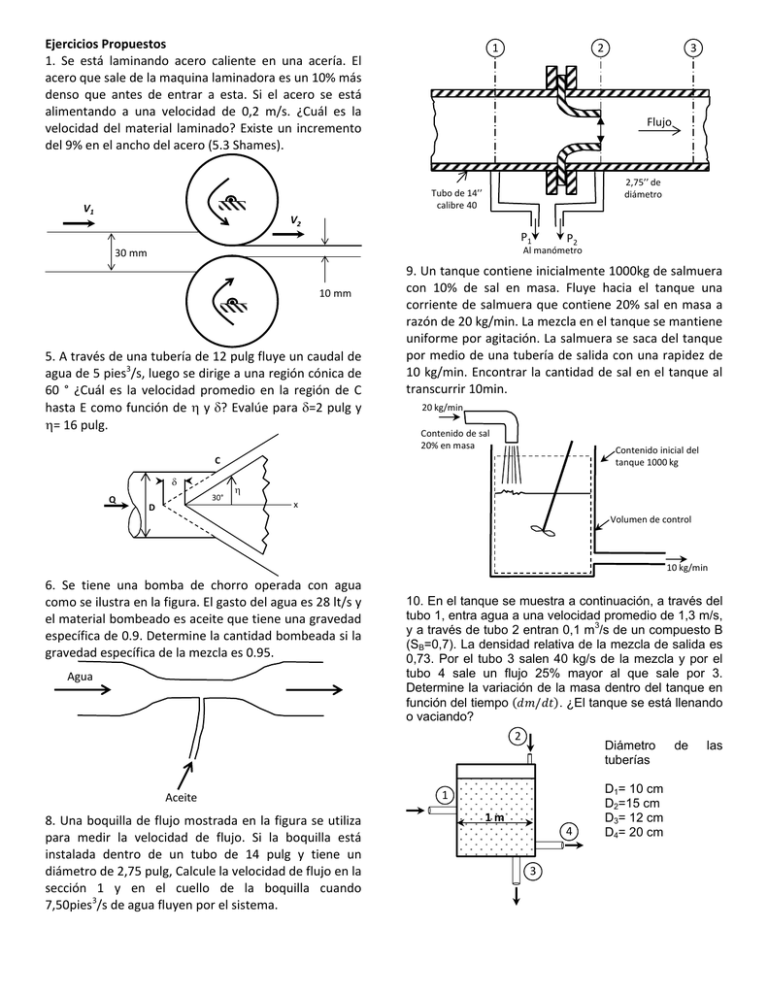
Ejercicios Propuestos
1. Se está laminando acero caliente en una acería. El
acero que sale de la maquina laminadora es un 10% más
denso que antes de entrar a esta. Si el acero se está
alimentando a una velocidad de 0,2 m/s. ¿Cuál es la
velocidad del material laminado? Existe un incremento
del 9% en el ancho del acero (5.3 Shames).
1
2
Flujo
2,75’’ de
diámetro
Tubo de 14’’
calibre 40
V1
3
V2
P1
P2
Al manómetro
30 mm
10 mm
5. A través de una tubería de 12 pulg fluye un caudal de
agua de 5 pies3/s, luego se dirige a una región cónica de
60 ° ¿Cuál es la velocidad promedio en la región de C
hasta E como función de  y ? Evalúe para =2 pulg y
= 16 pulg.
9. Un tanque contiene inicialmente 1000kg de salmuera
con 10% de sal en masa. Fluye hacia el tanque una
corriente de salmuera que contiene 20% sal en masa a
razón de 20 kg/min. La mezcla en el tanque se mantiene
uniforme por agitación. La salmuera se saca del tanque
por medio de una tubería de salida con una rapidez de
10 kg/min. Encontrar la cantidad de sal en el tanque al
transcurrir 10min.
20 kg/min
Contenido de sal
20% en masa
Contenido inicial del
tanque 1000 kg
C

Q
30°
D

x
Volumen de control
10 kg/min
6. Se tiene una bomba de chorro operada con agua
como se ilustra en la figura. El gasto del agua es 28 lt/s y
el material bombeado es aceite que tiene una gravedad
específica de 0.9. Determine la cantidad bombeada si la
gravedad específica de la mezcla es 0.95.
Agua
10. En el tanque se muestra a continuación, a través del
tubo 1, entra agua a una velocidad promedio de 1,3 m/s,
y a través de tubo 2 entran 0,1 m3/s de un compuesto B
(SB=0,7). La densidad relativa de la mezcla de salida es
0,73. Por el tubo 3 salen 40 kg/s de la mezcla y por el
tubo 4 sale un flujo 25% mayor al que sale por 3.
Determine la variación de la masa dentro del tanque en
). ¿El tanque se está llenando
función del tiempo (
o vaciando?
2
Aceite
8. Una boquilla de flujo mostrada en la figura se utiliza
para medir la velocidad de flujo. Si la boquilla está
instalada dentro de un tubo de 14 pulg y tiene un
diámetro de 2,75 pulg, Calcule la velocidad de flujo en la
sección 1 y en el cuello de la boquilla cuando
7,50pies3/s de agua fluyen por el sistema.
Diámetro
tuberías
1
1m
4
3
D1= 10 cm
D2=15 cm
D3= 12 cm
D4= 20 cm
de
las
2. Se fuerza agua hacia el interior del aparato con un
caudal de 0,1 m3/s a través del tubo A, a la vez que un
aceite con densidad relativa de 0,8 se fuerza con un
caudal de 0,03 m3/s a través del tubo B. Si los líquidos
son incompresibles y forman una mezcla homogénea de
gotas de aceite en el agua, ¿Cuál es la velocidad
promedio y la densidad de la mezcla que sale a través
del tubo C que tiene un diámetro de 0,3 m? (5.6 Shames)
B
Aceite
Donde
(
)
La densidad en C, será una contribución de lo que entra
por A y B, por definición:
C
Mezcla
(5)
D
Para saber la masa y el volumen de A (agua) y B (aceite)
que salen por C, se debe hacer una estimación basada
en lo que entra en un tiempo determinado. Por ejemplo
en un segundo como base de calculo
A
H2O
Resolución
Seleccionando como volumen de control el aparato y
aplicando la ecuación de conservación de la masa en su
forma integral
B
Aceite
C
Mezcla
Entonces la densidad de la mezcla
D
(6)
VC
Sustituyendo en la ecuación 4, la velocidad promedio en
el punto C será:
A
H2O
)
∑(
∑(
)
(1)
En estado estacionario, el terminó de acumulación se
anula, por lo que la ecuación anterior aparecen dos
términos de entrada y uno de salida, reacomodando
queda expresado como:
(
)
(
)
(
)
(2)
Expresando en función de los caudales
(
)
(
)
(
)
Despejando la velocidad de salida en C
( )
( )
( )
(3)
(4)
3. En el problema anterior, el pistón localizado en D
tiene un diámetro de 150 mm y se mueve hacia la
izquierda con una velocidad de 0,3 m/s ¿Cuál es la
velocidad promedio del fluido que sale por C?
7. Una enfermera extrae sangre de un paciente. El
pistón se hala con una velocidad de 0,25 pulg/s. Este
pistón permite el movimiento de aire alrededor de su
región periférica por medio de la holgura con el cilindro
de vidrio a una tasa de 0,001 pulg3/s. ¿Cuál es la
velocidad promedio del flujo de sangre en la aguja?
Cancelando las densidades a ambos lados de la igualdad
y despejando
(2)
Región II (AIRE)
¼ pulg/s
Pistón
(
)
(3)
di=0,02 pulg
Di=0,2 pulg
Cancelando las densidades a ambos lados de la igualdad
Aguja
(4)
Respuesta
En primer lugar debemos dividir la jeringa en por lo
menos dos regiones, la primera que es ocupada solo por
sangre (I) y la segunda que es ocupada por aire (II).
Donde
: Flujo volumétrico del aire que entra al cilindro de
vidrio [m3/s]
De la geometría podemos ver que
Entrada 2
Aire
(5)
Derivando a ambos lados de la igualdad respecto al
tiempo
Pistón
Aire (II)
hII
(6)
Sangre (I)
H
representa la velocidad de movimiento del pistón
Sustituyendo las ecuaciones 2 y 4 en 6, obtenemos
hI
(7)
Entrada 1
Sangre
Despejando
(
La ecuación de conservación de la masa en cada uno de
los volúmenes de control
Región I (SANGRE)
(
)
(1)
Donde
: Área transversal del cilindro de vidrio [m2]
: Velocidad promedio de la sangre en la aguja [m/s]
: Masa de la sangre dentro del cilindro de vidrio [kg]
) [
]
: 0,25 pulg/s
: 0,2 pulg
: 0,02 pulg/s
: 0,001 pulg3/s
La velocidad promedio de la sangre en la aguja será:
(8)
.
4. Hacia el interior de un tanque cilíndrico fluye agua a
través de un tubo 1 con una velocidad de 20 pies/s y sale
a través de los tubos 2 y 3 con velocidades de 8 y 10
pies/s respectivamente. En 4 hay una válvula de venteo
abierta a la atmosfera. Utilizando el volumen interno
completo del tanque como volumen de control ¿Cuál es
dh/dt? Los siguientes son los diámetros internos de los
tubos
(
)
(
)
(
)
(4)
Relacionando la altura del tanque con la altura del nivel
de agua (ver figura)
(5)
Derivando a ambos lados respecto al tiempo
(6)
Entonces
¿Cuál es la velocidad promedio del flujo de aire a través
de 4?, suponiendo que el flujo es incompresible
(7)
Sustituyendo en 4 y despejando
4
(
h
)
(
)
(
)
1
2 pies
3
2
Donde:
= 20 pies/s
= 0,049 pies2
= 8 pies/s
= 0,022 pies2
= 10 pies/s
= 0,034 pies2
Resolución
Realizando un balance de masa del agua en el tanque
)
∑(
)
∑(
(1)
(8)
= 3,14 pies2
Sustituyendo en 8,
4
El signo negativo en la variación de la altura, indica que
la altura se está reduciendo (zona del aire)
h
1
hT
2 pies
H
Para la parte B, basta con hacer un balance en la región
del aire, solo una salida de aire
3
(
2
)
(
)
(
)
(10)
(2)
La masa dentro del volumen de control puede ser
escrita como
(3)
Sustituyendo en 2
(9)
Cancelando la densidad a ambos lados de la igualdad y
despejando la velocidad del aire
Hay una entrada y dos salidas de agua, por lo que
(
)
Donde:
= 0,022 pies2