33 El interés compuesto y la amortización de préstamos

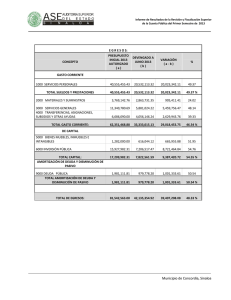
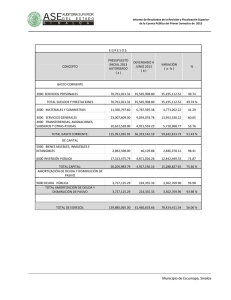
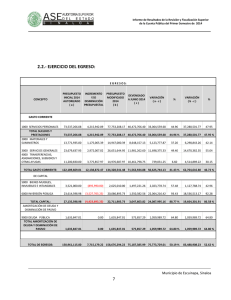
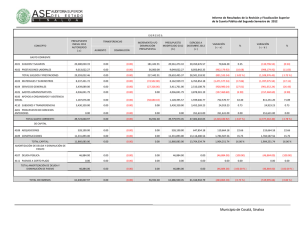
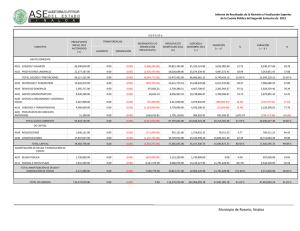
33 El interés compuesto y la amortización de préstamos.
33.01 El interés compuesto.
33.01.01 Concepto.
33.01.02 Valor actualizado de un capital.
33.01.03 Tiempo equivalente.
33.02 Amortización de préstamos.
33.02.01 Concepto.
33.02.02 Amortización por el método francés.
33.02.02.01 Concepto.
33.02.02.02 Cuadro de amortización.
33.02.03 Amortización por el método americano.
33.02.03.01 Concepto.
33.02.03.02 Cuadro de amortización.
INTRODUCCIÓN
Conocido el concepto de interés simple visto en la unidad anterior, vamos a analizar un
concepto nuevo: el interés compuesto.
El interés compuesto se basa en que los intereses devengados en un período se incorporan al
capital generando así nuevos intereses. El aumento de los intereses en el tiempo no será de
carácter lineal, como en el caso del interés simple, sino que tendrá carácter exponencial.
33.01 EL INTERÉS COMPUESTO
33.01.01 Concepto
Es importante tener presente al utilizar el interés compuesto, que el tipo de interés
aplicado en los períodos coincida en magnitudes temporales con los períodos utilizados,
es decir, si usamos como períodos temporales los trimestres, el tipo de interés a aplicar
será el tipo de interés trimestral. La formulación general será la siguiente:
S = C (1 + i) n
La expresión de la fórmula del interés compuesto se deduce a través de la definición
expuesta. En el primer período, el capital final que se obtendría sería:
S 1 = C + C x i = C (1 + i)
En el segundo período, el capital final del primer período se convierte en capital inicial de
este segundo período y por tanto el capital al final del segundo período sería:
S 2 = S 1 + S 1 x i = S 1 (1 + i) = C (1 + i) x (1 + i) = C (1 + i) 2
Siguiendo con esta ley de formación, el capital al final de "n" períodos sería:
Ejemplo: Cálculo del capital final (1)
Calcular el capital final de un capital inicial de 1.000 euros, colocadas al 20% anual
durante 3 años.
Solución:
S = 1.000 (1 + 0,2)3= 1.000 x 1,728 = 1.728 euros
Ejemplo: Cálculo del capital final (2)
Calcular el capital que se obtendría en el caso anterior si los intereses se devengaran
mensualmente.
Solución:
Tres años equivalen a 36 meses y el tipo de interés mensual aplicado será:
0,20
;
i =
12
36
0,20
S = 1.000
1 +
= 1.000 x 1,813 = 1.813
euros
12
NOTA: Recordemos la importancia de que exista homogeneidad temporal entre el tipo de
interés aplicado y los períodos, así si los períodos son meses, el tipo de interés
aplicado debe ser el mensual y no el anual.
Ejemplo: Cálculo de la tasa anual
Calcular la tasa anual equivalente de un interés nominal del 20% anual que se devenga
mensualmente.
NOTA: Este caso es muy frecuente hallarlo en la práctica, pues un banco nos concede un
préstamo con un tipo de interés anual del 20% y luego nos resulta una tasa anual
equivalente superior al 20%, debido a que el devengo de intereses es mensual.
Solución:
12
0,20
1 + i
;
1 +
=
12
donde "i" es la tasa anual equivalente, correspondiente al tipo de interés nominal del 20%
anual que se devenga mensualmente.
0,20
i = 1
12
- 1
+
=
21,94%
12
0,2194
=
Esta ecuación nos expresa la equivalencia de un capital unitario, usando la tasa anual
equivalente y por tanto el capital al final del año sería: 1 + i; con este mismo valor del
capital al final del año usando un interés mensual, fruto de dividir el interés nominal anual
entre los 12 meses de un año.
Lógicamente, la tasa anual equivalente es mayor que el interés nominal anual, ya que en
este último caso los intereses generados por el capital mes a mes generan nuevos
intereses, constituyendo al final de año un capital superior del que resultaría de aplicar al
capital inicial el tipo de interés nominal anual.
Ejemplo: Cálculo de tiempo
Calcular el tiempo necesario para que un capital de 1.000 de euros se convierta en 2.000,
con
un
tipo
de
interés
anual
del
20%
convertible
semestralmente.
Solución:
S = C (1 + i) t
t
0,20
2000
=
1 +
1.000
2
Observemos que al usar semestres, el tipo de interés que figura en la fórmula del interés
compuesto es semestral y se obtiene dividiendo el tipo anual entre el número de
semestres del año.
Para resolver esta ecuación debemos usar logaritmos:
2.000
0,20
=
1 +
2
1.000
0,20
2 =
t
1 +
t
0,20
log 2 = log
2
1 +
2
t
log 2 = 0,3010 = t x log 1,1
0,3010
0,3010
t =
=
= 7,27 semestres = 3,6 años
log 1,1
0,0414
es decir: 3 años, 7 meses y 9 días
365 días
Su cálculo ha sido: 0,6 años x
= 219 días
1 año
que tomando un mes con 30 días
33.01.02
7 meses y 9 días
Valor actualizado de un capital
En el apartado anterior se ha aprendido a constituir un capital, al final de una serie de
períodos y con un tipo de interés determinado, a partir de un capital inicial.
En este apartado actuaremos en sentido inverso, hallando el valor actual de un capital
situado
en
un
instante
de
tiempo
posterior
al
actual.
La formulación básica será la del interés compuesto, pues conocido el capital final, el
capital inicial lo obtendríamos:
S
C =
(1 + i)
n
Este proceso se conoce en la matemática financiera con el nombre de actualización,
mientras que el del apartado anterior se conoce con el nombre de capitalización.
Ejemplo: Valor actualizado de un capital (1)
Hallar el valor actual de 1.000 euros a pagar dentro de 3 años, con una tasa de interés del
16%
anual
convertible
trimestralmente.
Solución:
0,16
1.000 = C
1 +
4
1.000 = C (1,04)
12
12
1.000
1.000
=
C =
= 624,61 euros
12
1,04
1,6010
Es decir, que este valor de "C" colocado al 16% anual, con intereses devengados
trimestralmente durante 3 años (12 trimestres), nos daría 1.000 euros al final del tercer
año.
Ejemplo: Valor actualizado de un capital (2)
Se establece la devolución de una deuda del siguiente modo 1.000 euros a pagar dentro
de un año y otro millón de euros a pagar dentro de tres años, con un tipo de interés del
16% anual. Calcular el capital a pagar si se establece la fecha de devolución dentro de dos
años.
Solución:
Para resolver este problema debemos unificar los capitales expuestos a un mismo instante
de tiempo. Si los actualizamos, la ecuación que resuelve el problema sería:
x
1.000
=
1.000
+
(1 + 0,16) 2
(1 + 0,16)
1.000 (1 + 0,16) 2
x =
(1 + 0,16) 3
1.000 (1 + 0,16) 2
+
(1 + 0,16)
(1 + 0,16) 3
1.000
x
=
1.000
(1 +
0,16)
=
+
1.160.000 + 862.069 =
2.022,069 euros
(1 + 0,16)
33.01.03
Tiempo equivalente
Se trata de determinar la fecha en la que un conjunto de pagos, con vencimientos
distintos, pueden ser sustituidos por un pago único. El tiempo transcurrido hasta dicha
fecha
se
denomina
tiempo
equivalente.
Como vemos, no es más que una variante del caso práctico anterior, en el que en lugar de
hallar el capital en una determinada fecha, se trata de fijar un capital y hallar dicha fecha.
Ejemplo: Tiempo equivalente
Hallar el tiempo equivalente para el pago de una deuda de 1.000 euros trimestrales,
durante 2 años, con una tasa de interés del 20% anual convertible trimestralmente,
efectuando
un
pago
de
8.000
euros.
Solución:
Realizando la actualización de estos valores obtendremos la ecuación que resuelve el
problema.
0,2
= 0,05
i =
4
8.000
1.000
1.000
=
(1 + 0,05) t
1.000
+
1 + 0,05
8.000
(1 + 0,05) 2
1
=1.000
(1 + 0,05) t
1.000
+
+ ... +
(1 + 0,05) 3
1
+
1
+
1,05 2
1,05
(1 + 0,05) 8
1
+...+
1,05 3
1,05 8
NOTA: Observemos que los términos del corchete forman una progresión geométrica,
cuya suma se calculará según lo expuesto en la unidad didáctica anterior al
respecto. La expresión usada está simplificada y su desarrollo se verá en
33.02.02.01.
1
1 8.000
(1 + 0,05) 8
= 1.000
(1 + 0,05) t
0,05
8.000
= 1.000 x 6,463 = 6.463
(1 + 0,05) t
8.000.000
= (1 + 0,05) t
6.463.000
1,238 = (1 + 0,05) t
log 1,238 = t x log 1,05
log 1,238
= 4,37 trimestres
i =
log 1,05
33.02
AMORTIZACIÓN DE PRÉSTAMOS
33.02.01
Concepto
Amortizar un préstamo significa devolver un capital, objeto del préstamo, en un plazo de
tiempo
y
a
un
tipo
de
interés
determinado.
Las formas en que se puede devolver o amortizar el préstamo son variadas y en esta
unidad se estudiarán los dos métodos, que a nuestro modo de entender, son los más
usados en la vida actual, el método francés y el método americano.
En general, se trata de una prestación única y una contraprestación múltiple, con una
serie de pagos en determinados instantes de tiempo, cuya finalidad es extinguir la deuda.
Los tipos de interés de los períodos pueden ser distintos, en general. Gráficamente sería:
Donde el significado de las variables sería:
Co: capital prestado.
as: términos amortizativos, que son los pagos realizados.
ts: tiempos en los que se efectúan los pagos.
is: tipos de interés de los correspondientes períodos.
En función de las posibilidades de variación que ofrecen todas estas variables, aparecen
las distintas formas de devolución de los préstamos.
33.02.02
Amortización por el método francés
33.02.02.01
Concepto
En este caso todos los términos amortizativos son iguales, así como los tipos de interés y
se pagan al final de cada período. El esquema gráfico sería:
Para determinar la cuantía de los términos amortizativos procederíamos del siguiente
modo:
a
a
a
+
C =
+
1+i
(1 + i)2
(1 + i)3
1
1
1+i
(1 + 1)n
1
+
C = a
a
+ ... +
+ ... +
(1 + 1)n
(1 + i)2
NOTA: Observe que los términos del corchete forman una progresión geométrica y para
su suma procedemos a aplicar la fórmula expuesta en la unidad anterior:
a1
(rn - 1)
S =
r-1
1
1
- 1
C = a
=
1
- 1
1+i
1
1
- 1
=
C = a
1 - (1 + i)
1+i
1
- 1
C
(1 + i)n
=
=
1-1-i
1
1 (1 + i)n
C = a
=
a
a
x
i
NOTA: ani es la expresión de la suma de la serie geométrica que se utilizó para resolver
el ejemplo sobre el Tiempo equivalente de la sección anterior.
De forma que la cuantía de los términos amortizativos la encontraremos usando la fórmula:
C
a =
1
1 (1 + i)n
i
Dentro del término amortizativo una parte corresponde a devolución del préstamo y la otra
al pago de intereses. Para determinarlas procederemos del siguiente modo:
Sea Cs-1 y Cs los capitales pendientes de devolver al final de los períodos "s-1" y "s"
respectivamente.
Se verificará la ecuación general:
Cs = Cs-1 (1 + is) - as
que no es más que trasladar los capitales del gráfico al instante "ts", teniendo en cuenta
que el capital pendiente al final del período "s-1" ya contiene el término amortizativo "as-1".
En el método francés esta ecuación nos queda:
Cs = Cs-1 (1 + i) - a
La diferencia: As = Cs-1 - Cs; nos da la parte del capital devuelto en el período en cuestión.
Por tanto la ecuación nos indica:
Cs-1 - Cs = As = a - Cs-1 x i
donde "As" es la cuota de amortización o capital devuelto en el período y "Cs-1 x i", son los
intereses pagados en este período, que denominaremos, "Is". Así pues nos queda:
a = As + Is siendo Is = Cs-1 x i
Luego para saber el capital devuelto del préstamo, "As", haremos:
As = a - Is = a - Cs-1 x i
33.02.02.02
Cuadro de amortización
Para la construcción del cuadro de amortización de un préstamo por el método francés es
necesario, en primer lugar, conocer la cuantía de los términos amortizativos, "a", para así
poder calcular los intereses, la cuota de amortización y el capital pendiente al final de cada
período.
La forma de representar el cuadro de amortización sería:
Término Intereses
Período amortizat.
as
Is
Inicio
1
2
3
•
•
•
•
•
•
--a
a
a
•
•
•
•
•
•
Cuota de
amortizac.
As
Capital
amortizado
Ms
------I1 = Co x i A1 = a - Co x i M1 = a - Co x i
I2 = C1 x i A2 = a - C1 x i M2 = A1 + A2
I3 = C2 x i A3 = a - C2 x i M3 = A1 + A2 + A3
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Capital pdte.
de amortiz.
Cs
Co
C1 = Co - A1
C2 = C1 - A2
C3 = C2 - A3
•
•
•
•
•
•
Conocido el término amortizativo "a" mediante la fórmula expuesta en el apartado anterior,
se procede al cálculo de los intereses del período multiplicando el capital pendiente de
al
inicio
del
período
por
el
tipo
de
interés
"i".
amortizar
"Cs",
A continuación podremos calcular el capital amortizado "A", por diferencia entre el término
amortizativo y los intereses del período. Por último, el capital pendiente de amortizar "Cs",
al final de cada período se calculará por diferencia entre el capital pendiente de amortizar
en el período anterior "Cs-1" y la cuota de amortización "As", del período en cuestión.
La columna de capital amortizado, se forma por suma en cada período de todas las cuotas
de amortización, As, de períodos anteriores, incluida la del período en cuestión.
Ejemplo: Cuadro de amortización por el método francés
Construir el cuadro de amortización de un préstamo de 1.000.000 euros, con cuotas
pagaderas anualmente, de duración 8 años a un tipo de interés del 10%.
Solución:
Calculemos la cuantía de los términos amortizativos.
1.000.000
a =
1.000.000
=
= 187.444,02
1
1 (1 + 0,1)8
A partir de aquí, los intereses del primer período se calcularían:
I1 = Co x i = 1.000.000 x 0,1 = 100.000
La cuota de amortización o capital amortizado, devuelto o extinguido en el primer
período, sería:
A1 = a - I1 = 187.444,02 - 100.000 = 87.444,02
El capital pendiente de amortizar al final del primer período o inicio del segundo sería:
C1 = Co - A1 = 1.000.000 - 87.444,02 = 912.555,98
Para el siguiente período procederíamos de forma similar, si bien el término
amortizativo, "a", es el mismo para todos los períodos, por lo que empezaríamos por
calcular los intereses de este segundo período:
I2 = C1 x i = 912.555,98 x 0,1 = 91.255,6
La cuota de amortización del segundo período sería:
A2 = a - I2 = 187.444,02 - 91.255,6 = 96.188,42
El capital amortizado hasta este período sería:
M2 = A1 + A2 = 87.444,02 + 96.188,42 = 183.632,44
El capital pendiente de amortizar al final de este período:
C2 = C1 - A2 = 912.555,98 - 96.188,42 = 816.367,56
El resto de cálculos quedarán reflejados en el cuadro de amortización.
Término
Período amortizat.
as
Inicio
1
2
3
4
5
6
7
8
--187.444,02
187.444,02
187.444,02
187.444,02
187.444,02
187.444,02
187.444,02
187.444,02
Intereses
Is
--100.000
91.255,6
81.636,76
71.056,02
59.417,24
46.614,56
32.531,61
17.040,37
Cuota de
Capital
Capital pdte.
amortizac. amortizado de amortiz.
As
Ms
Cs
--87.444,02
96.188,42
105.807,26
116.388
128.026,78
140.829,46
154.912,41
170.403,65
--87.444,02
183.632,44
289.439,70
405.827,70
533.854,48
674.683,94
829.596,35
1.000.000
33.02.03
Amortización por el método americano
33.02.03.01
Concepto
1.000.000
912.555,98
816.367,56
710.560,30
594.172,30
466.145,52
325.316,06
170.403,65
0
Este método consiste, en pagar en cada vencimiento los intereses del período y en el
último vencimiento se pagan intereses y la devolución del capital prestado.
Es evidente, que a la vista de lo expuesto, las cuotas de amortización al final de cada uno
de los períodos son nulas a excepción de la última, pues únicamente se pagan los
intereses de dichos períodos. Los términos amortizativos coincidirán en cuantía con los
intereses del período:
as = As + Is; As = 0
as = Is
Además, como consecuencia de ello, el capital pendiente de amortizar al final de cada uno
de los períodos, siempre será el mismo e igual al capital inicial objeto del préstamo, "Co".
El esquema de este método sería:
Donde se observa que los términos amortizativos son del tipo:
as = Co x is = Is
Las cuotas de amortización, nulas en todos los períodos, a excepción del último en el que
la cuota de amortización coincidirá con el capital inicial objeto del préstamo.
El gráfico siguiente, muestra la evolución de la amortización del préstamo por este método:
La última cuota de amortización sería:
An = Co + Co x in
33.02.03.02
Cuadro de amortización
La estructura del cuadro de amortización es muy simple, debido a la facilidad y sencillez
de cálculo de los diversos parámetros que configuran el cuadro de amortización. De forma
directa podremos calcular todos los términos amortizativos, "as", de los distintos períodos,
como producto del capital inicial por el tipo de interés del período en cuestión. Los
intereses coincidirán con dichos términos amortizativos, pues las cuotas de amortización
son todas nulas a excepción de la última que coincide con la cuantía del capital inicial.
El capital amortizado es nulo en todos los períodos, a excepción del último en que se
amortiza
el
total.
Así pues, el cuadro de amortización sería:
Término
Período amortizat.
as
Inicio
1
2
3
•
•
•
•
•
n
Intereses
Is
----a1 = Co x i1 I1 = Co x i1
a2 = Co x i2 I2 = Co x i2
a3 = Co x i3 I3 = Co x i3
•
•
•
•
•
•
•
•
•
•
Co x in + An Co x in
Cuota de
Capital Capital pdte.
amortizac. amortizado de amortiz.
As
Ms
Cs
--------•
•
•
•
•
An = Co
--------•
•
•
•
•
Co
Co
Co
Co
Co
•
•
•
•
•
0
Ejemplo: Cuadro de amortización por el método americano
Construir el cuadro de amortización correspondiente a un préstamo de 1.000.000 de euros,
con cuotas pagaderas anualmente, de duración 5 años, a un tipo de interés del 15%
durante los tres primeros años y a un tipo del 10% durante los dos últimos.
Solución:
El cálculo de los términos amortizativos y de los intereses será:
a1
a2
a3
a4
a5
=
=
=
=
=
=
I1 = Co x i1 = 1.000.000 x 0,15 = 150.000
I2 = Co x i2 = 1.000.000 x 0,15 = 150.000
I3 = Co x i3 = 1.000.000 x 0,15 = 150.000
I4 = Co x i4 = 1.000.000 x 0,10 = 100.000
A5 + I5 = A5 + Co x i5 = A5 + 1.000.000 x 0,10 = 1.000.000 + 100.000 =
1.100.000
El cuadro de amortización sería:
Término Intereses Cuota de
Capital Capital pdte.
Período amortizat.
amortizac. amortizado de amortiz.
as
Is
As
Ms
Cs
Inicio
1
2
3
4
5
--150.000
150.000
150.000
100.000
1.100.000
------150.000
----150.000
----150.000
----100.000
----100.000 1.000.000 1.000.000
1.000.000
1.000.000
1.000.000
1.000.000
1.000.000
Durante la presente unidad hemos aprendido conceptos nuevos: la actualización, la
capitalización y la amortización.
La actualización consiste en calcular el valor actual de un capital situado en un instante de
tiempo posterior al actual.
La capitalización consiste en calcular, desde un capital actual, lo que este capital valdrá en
un periodo de años.
La amortización de préstamos es la devolución del capital solicitado. Este puede ser
devuelto (amortizado) de acuerdo con el método francés o el americano.
Ahora ya podemos saber, si tenemos una hipoteca, cual es el mejor método para nuestra
economía.