IB V IB V - prof.usb.ve.

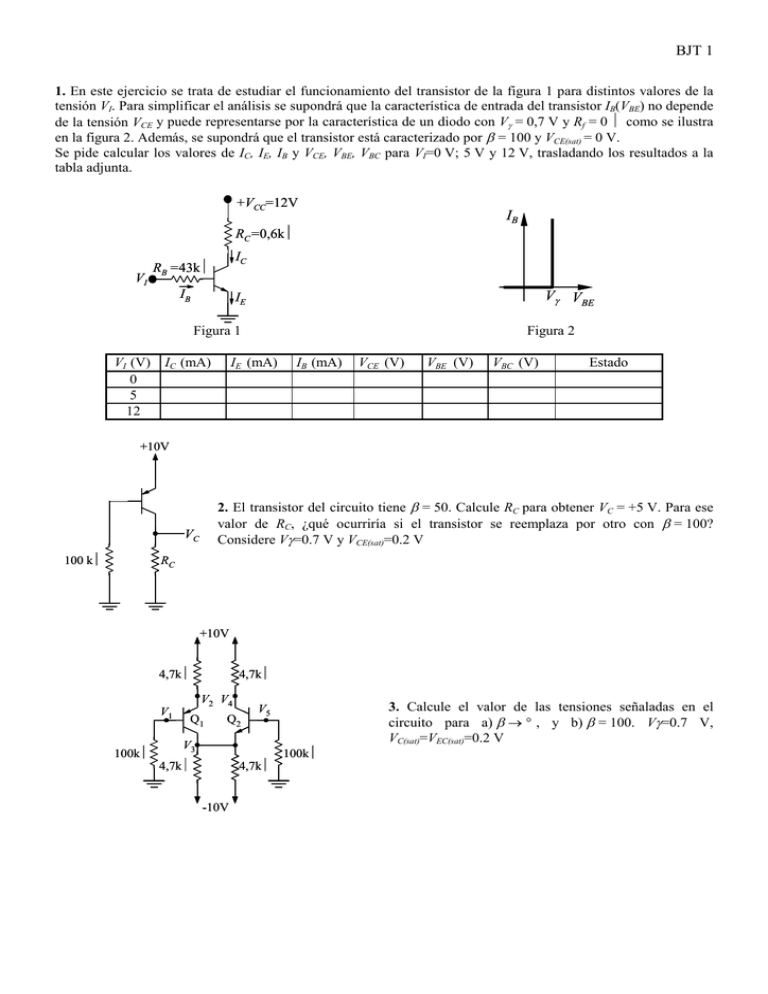
BJT 1
1. En este ejercicio se trata de estudiar el funcionamiento del transistor de la figura 1 para distintos valores de la
tensión VI. Para simplificar el análisis se supondrá que la característica de entrada del transistor IB(VBE) no depende
de la tensión VCE y puede representarse por la característica de un diodo con Vγ = 0,7 V y Rf = 0 Ω como se ilustra
en la figura 2. Además, se supondrá que el transistor está caracterizado por β = 100 y VCE(sat) = 0 V.
Se pide calcular los valores de IC, IE, IB y VCE, VBE, VBC para VI=0 V; 5 V y 12 V, trasladando los resultados a la
tabla adjunta.
+VCC=12V
IB
RC=0,6kΩ
VI
IC
RB =43kΩ
IB
Vγ VBE
IE
Figura 1
VI (V)
0
5
12
IC (mA)
Figura 2
IE (mA)
IB (mA)
VCE (V)
VBE (V)
VBC (V)
Estado
+10V
2. El transistor del circuito tiene β = 50. Calcule RC para obtener VC = +5 V. Para ese
valor de RC, ¿qué ocurriría si el transistor se reemplaza por otro con β = 100?
Considere Vγ=0.7 V y VCE(sat)=0.2 V
VC
RC
100 kΩ
+10V
4,7kΩ
4,7kΩ
V1
100kΩ
V2 V4
Q1
Q2
3. Calcule el valor de las tensiones señaladas en el
circuito para a) β → ∞, y b) β = 100. Vγ=0.7 V,
VC(sat)=VEC(sat)=0.2 V
V5
V3
100kΩ
4,7kΩ
4,7kΩ
--10V
BJT 2
4. En los circuitos integrados es habitual limitar la corriente IL
que entrega el circuito en colector común de la figura 1
modificándolo según muestra la figura 2. En régimen de
funcionamiento normal (sin limitación de corriente) , el
transistor T1 está en activa y el T2 en corte. Para el circuito de
la figura 2:
a) Expresar IL en función de IIN en régimen de funcionamiento
normal
b) ¿Qué condición debe cumplir IL para que T1 funcione en
activa? Suponga que T1 no puede estar saturado
c) Calcular el máximo valor de IL para el que T2 está en corte
d) Para el valor de IL calculado en c), comprobar que T1 no
está saturado
DATOS: VCC = 10 V, RL = 300 Ω, R = 25 Ω. Para ambos
transistores, β = 50, VγE = 0,7 V, VCE(sat) = 0,2 V
VCC
VCC
T1
T1
T2
R
IIN
RL
IL
IIN
Figura 1
DATOS:
VCC = 5 V, RA = 1,7 kΩ, RB = 0,4 kΩ, RC = 6 kΩ; transistores: β = 100,
VγE = VBE(ON) = 0,7 V, VCE(sat) = 0,2 V
IL
Figura 2
VCC
5. Los tres transistores bipolares del circuito de la figura son idénticos, y
para este ejercicio se pueden caracterizar por un modelo lineal por tramos.
Se sabe que T2 está en saturación.
a) De los cuatro estados posibles del transistor (activa directa, saturación,
corte y activa inversa), deduzca en cuál de ellos se encuentra T1
b) Calcule el rango de valores de RD para el que T3 está en activa
c) Para RD = 60 Ω T3 está en saturación y se mide una caída de tensión en
sus bornas de 0,7 V. Calcule los valores de las corrientes IC2 e IC3.
Compruebe que T2 y T3 están saturados
RL
RA
I C3
RB
T3
I E3
RC
RC
RD
IC2
T1
T2
6. La figura 1 muestra el símbolo circuital del llamado transistor Schottky, dispositivo que se emplea en la
tecnología digital TTL de alta velocidad. Este transistor se realiza conectando un diodo Schottky (es decir, de unión
metal-semiconductor) entre la base y el colector de un transistor bipolar convencional, como se indica en la figura
2. Se pide:
a) Obtener las expresiones de IE e IC en función de VBE
C
C
y VBC para el funcionamiento del transistor Schottky
IC
D
IC
S
en estática, utilizando el modelo de Ebers-Moll para
el transistor TB y la ecuación de Shockley del diodo
IB
DS (suponga conocidos los parámetros de dichos
B
TB
B
modelos)
I
B
b) Considerando los modelos lineales por tramos para
TB y DS, demostrar que el transistor TB nunca opera
en la región de saturación
IE
IE
c) Si el transistor TB está polarizado en modo activo
E
E
con VCE = 4 V, ¿en qué estado se encuentra el diodo
Figura 1
Figura 2
DS? Utilice también el modelo lineal por tramos
DATOS de los modelos lineales por tramos:
Transistor TB: VγE = 0,7 V; VCE,sat = 0,2 V. Diodo DS: Vγ = 0,3 V; VZ = 5 V; RF =0
BJT 3
7. Con el circuito de la figura, que contiene un BJT trabajando en saturación, se
desea analizar la influencia de las aproximaciones de las tensiones en el cálculo de
VCC
las corrientes. Para ello se va a realizar un cálculo más preciso de las tensiones y
corrientes del BJT mediante un proceso iterativo. Si se aplica al circuito una
tensión VI = 10 V, se pide:
RC IC
a) Obtener un valor aproximado de IE e IC. Para ello suponga VCE = 0,1 V y
VBE = 0,6 V, es decir, se utiliza un modelo aproximado por tramos lineales
RB
b) Utilizando las ecuaciones de Ebers-Moll y los valores de IC e IE obtenidos en el
vI
apartado a), calcular nuevos valores para VCE y VBE
IB
IE
c) Con estos valores de las tensiones recalcule las corrientes IC e IE
d) ¿Cuánto difieren, en tanto por ciento, los valores de IC e IE calculados en a) y
c)?
DATOS:
Del circuito: RB = RC = 1 kΩ; VCC = 15 V; vI = 10 V; del BJT: IS = 9,9 10-14 A; αF = 0,99; αR = 0,1; VT = 25 mV
8. El circuito de la figura, con la polaridad indicada para VCC, garantiza un punto
de trabajo Q en la región activa para transistores npn con cualquier valor de β . Se
utilizará un modelo de transistor en activa con características independientes de
VCE: las de entrada del tipo de diodo de Shockley IB(VBE,VCE) = I0 (exp(VBE/VT)-1),
y las de salida del tipo β = cte, es decir, IC(VCE,IB) = β IB
a) Demostrar que, cualesquiera que sean β , RB, RC yVCC > 0, el transistor bipolar
npn nunca se encontrará en saturación en ese circuito, es decir, VCB ≥ 0 siempre
b) Con los valores RB = 100 kΩ, RC = 2 kΩ, VCC = 10 V y un transistor de
β = 100, determinar el punto de trabajo Q, es decir, IB, IC y VCE, utilizando una
aproximación razonable para el valor de VBE, que deberá indicarse
c) El transistor anterior funciona a una temperatura para la que I0 = 10-10 µA y
VT = 25 mV. Obtener una mejor aproximación para el valor de VBE, precisando
hasta el mV
d) Si se utilizara, en el mismo circuito y a la misma temperatura, un transistor con
un áre de unión base – emisor 4 veces mayor, ¿es correcto suponer que esta
diferencia tendrá muy poco efecto sobre el punto de trabajo? Justificar la
respuesta
9. Los transistores de la figura, sean npn o pnp, tienen
VCC
idénticos parámetros de Ebers-Moll. Los diodos LED de
L1
esta figura se suponen ideales (ID = 0 si VD < 0, VD = 0 si
ID > 0). Se considerará que cada LED emite luz detectable
V1
cuando por él circula una corriente mayor de 10 mA. Se
pide:
0V
a) Condición que debe cumplir V1 para que L1 emita
b) Condición que debe cumplir V2 para que L2 emita
c)
Condición que debe cumplir V3 para que L3 emita
DATOS: VCC = 10 V, VT = 26,5 mV, IS = 0,5 pA, αF = αR = 0,5
NOTAS: Presente los resultados numéricos con al menos 3 cifras significativas
VCC
RB R C
IC
IB
L2
V2
L3
V3
10. Cuando el BJT del circuito de la figura 1 funciona en activa con altas corrientes de colector iC, el parámetro
β F = iC/iB no es constante sino que disminuye con iC según muestra la figura 2. En este ejercicio se trata de analizar
algunos efectos que esto conlleva, y para ello se pide:
BJT 4
a) Expresar β F en función de iC para
iC > IM utilizando los datos que
aparecen en la figura 2
b) Calcular VO en el circuito de la figura
IB
RC
1 para IB = 5 mA, comprobando que
funciona en activa
VO
c) Lo mismo, para IB = 20 mA
d) Calcular el parámetro de pequeña
i
di
señal del BJT β f = c ≡ C para
i b di B
Figura 1
IB = 20 mA
DATOS: VCC = 10 V, RC = 6 Ω, VCE(sat) = 0,2 V, β 0 = 100, IM = 1 A
βF(iC)
VCC
βΟ
βΟ
2
11. El conjunto de tres transistores bipolares T1, T2 y T3
acoplados según muestra la figura 1 funciona como el
transistor npn equivalente representado en la figura 2. Se
pide calcular:
a) El parámetro β del transistor equivalente definido
como el cociente IC/IB de las corrientes indicadas en
T3
la figura 2 cuando T1, T2 y T3 están en activa
b) La mínima tensión VCE en el transistor equivalente
B
T1
para la que T1, T2 y T3 están en activa con IB > 0.
Considere para este apartado el modelo lineal por
tramos para los transistores
c) El valor VBE2-VBE1 cuando T1, T2 y T3 están en
Figura 1
activa. Considere para este apartado el modelo de
Ebers-Moll para los transistores en activa, y exprese
el resultado con tres cifras significativas
DATOS: VT = 25 mV. Para todos los BJT: β = 10, |VA| → ∞
Modelo lineal por tramos: VγE ≅ 0,7 V, |VCE(sat)| ≅ 0,2 V
Modelo de Ebers-Moll en activa: IC = β IB, IB = I0 exp(|VBE|/VT)
iC
2IM
IM
Figura 2
C
C
IC
B
T2
IB
IE
E
E
Figura 2
12. La figura muestra un circuito “multiplicador de vBE”
que realiza la función de mantener en sus terminales una
tensión aproximadamente proporcional a la tensión vBE
del BJT. Para su correcto funcionamiento, la corriente de
base iB debe ser despreciable en el nodo B. Sabiendo que
el BJT funciona en activa:
a) Calcule el valor de M que cumple que v ≅ M vBE
R
suponiendo que iB es despreciable en el nodo B
b) Si se ha medido V = 1860 mV y VBE = 610 mV,
calcule el valor del parámetro IES (= IS/αF) del BJT
c) En el punto de trabajo del apartado b), calcule la
resistencia equivalente del circuito como DATOS: R = 1 kΩ, VT = 26 mV; del BJT: β F = 50,
componente de dos terminales para pequeña señal a ro → ∞
frecuencias medias
⇔
BJT 5
VCC=+10V
RC=
3kΩ
13.
a) Un valor de β muy elevado puede hacer que el transistor de la figura esté
saturado incluso sin señal aplicada. Calcule el mínimo valor de β para el
que ocurre esto.
b) Demuestre que la ganancia de tensión del circuito vo/vi (con el transistor
en activa directa) varía linealmente con β
DATOS: VT = 0,025 V, VCE(sat) = 0,2 V, VBE ≅ 0,7 V
vO
RBB=
100kΩ
vi
VBB
=3V
V+=+10V
C→∞
14.
a) Calcule la ganancia de tensión del circuito de la figura, vo/vi
b) Repita a) si la fuente de señal presenta una resistencia interna (no
dibujada) Rg = 100 Ω
DATOS: kT/e = 0,025 V, VEC,sat = 0,2 V, VEB ≅ 0,7 V, β = 100
RE=
10kΩ
vi
RC=
5 kΩ
C→∞
V-=-10V
+VCC
15.
Calcule y represente gráficamente la función vO(vI) para el circuito de la
figura, y diga si puede utilizarse para realizar alguna función lógica sobre
señales digitales de niveles ≅ 0 y 5V y de qué función se trata.
VCC = 5 V; RB = 25 kΩ; RC = 700 Ω; VγE = 0,7 V; VEC,sat = 0,3 V; β = 100
vI
RB
vO
RC
vo