Funciones de varias variables.

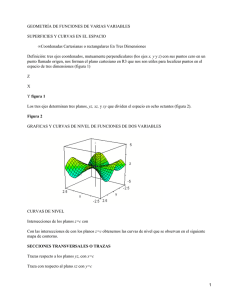
Introducción a las funciones de varias variables
Funciones de varias variables.
Definición.
Hasta ahora se han estudiado funciones de la forma y = f (x) ,
f :D ⊂
→
Estas funciones recibían el nombre de funciones reales de variable real ya que su valor y
dependía de una sola variable x. En este apartado se estudian funciones cuyo valor depende de más
de una variable. Estas funciones reciben el nombre global de funciones de varias variables o
funciones de variable vectorial. Algunos ejemplos de las mismas son:
EJEMPLO:
f ( x, y ) = 3 x 3 + xy + sen (2 x + 7 y 2 ) ; g ( x1 , x2 , x3 ) = x1 + 3 x2 + x1 x2 + 5 ln ( x1 + x2 + x3 )
son funciones reales de dos y tres variables respectivamente.
f ( x, y ) = (3 x 2 + xy 3 ,3 x + 2 y, x + y + 1) ; g ( x1, x2 , x3 ) = ( x1 + 3x2 , x1 x2 , cos ( x1x3 ),2 y − xy 3 )
también son funciones de varias variables pero aquí el resultado de la función es un vector por
eso se llaman funciones vectoriales de variable vectorial.
Para determinar completamente esta idea e función de varias variables se da la siguiente:
Definición: Se denomina función de varias variables con dominio de definición D ⊂
con n > 1 entero y m entero, a cualquier aplicación de la forma:
f :D ⊂ n → m
n
,
NOTAS: 1.- Estas funciones también se denominan funciones de variable vectorial donde:
-
n
es el conjunto inicial.
-
m
es el conjunto final.
- D ⊂ n es el dominio de la función.
- f (D) ⊂ m es el recorrido de la función.
2.- Cuando m = 1 la función se llama función real de variable vectorial o, de forma más
breve, campo escalar (esta nomenclatura se utiliza sobre todo en física).
3.- Cuando m > 1 la función recibe el nombre de función vectorial de variable vectorial o
campo vectorial. El valor m se denomina dimensión de la función. En ese caso la función se
representa por el símbolo f (esto es se pone una flechita sobre la letra que le da nombre).
EJEMPLO: En el ejemplo anterior se han presentado:
f ( x, y ) un campo escalar de dos variables.
g ( x1, x2 , x3 ) un campo escalar de tres variables.
1
Introducción a las funciones de varias variables
f ( x, y ) un campo vectorial de dos variables y dimensión dos.
g ( x1, x2 , x3 ) un campo vectorial de tres variables y dimensión cuatro.
Existen situaciones del mundo real que se estudian mediante funciones de este tipo.
Así, la función que a cada punto ( x, y, z ) de una habitación con calefacción le hace
corresponder su temperatura es un campo escalar de tres variables. Y la función que a cada
punto ( x, y, z ) de una sala ventilada le hace corresponder un vector que representa la
velocidad del aire (en magnitud y dirección) en dicho punto es un campo vectorial de
dimensión tres y tres variables.
de
n
4.- Cuando no se especifica el domino de definición D se entiende que el mayor subconjunto
para el que la función tenga sentido.
5.- Para completar todas las posibilidades hay que
hablar de lasm funciones vectoriales de
. En general representan
variable real que se ajustan a un esquema de la forma: f : D ⊂ →
curvas en un espacio de dos o más dimensiones.
6.- Formas de expresión: en este apartado se estudiarán, sobre todo, campos escalares de dos
o tres variables. Estas funciones suelen venir expresadas de dos formas:
6.1.- Forma explícita donde la función se presenta del modo expuesto anteriormente:
f ( x, y ) = 3 x 3 + xy + sen (2 x + 7 y 2 ) , que a veces se suele expresar de la forma
f ( x, y ) = z con z = 3 x 3 + xy + sen (2 x + 7 y 2 )
g ( x1 , x2 , x3 ) = x1 + 3 x2 + x1 x2 + 5 ln ( x1 + x2 + x3 ) , que también se expresa como
g ( x1 , x2 , x3 ) = w con w = x1 + 3 x2 + x1 x2 + 5 ln ( x1 + x2 + x3 )
6.2. Forma implícita, donde el valor de la función z se presenta por medio de una ecuación
con sus variables (en la que en ocasiones no es posible despejar dicho valor). Por ejemplo:
f ( x, y ) = z con xy 2 z + ln( x + yx) − cos( x 3 y 2 z 4 ) − 3 = 0
El estudio da campos escalares de dimensiones superiores es análogo a estos. En el caso de
campos vectoriales, se hace por componentes (cada una de las cuales es un campo escalar).
Estudio sin derivar.
Cuando se estudian estas funciones, como en el caso general de cualquier tipo de función, en
primer lugar hay que centrarse en las informaciones que se pueden obtener de la simple definición
de la función. Luego se profundiza este estudio con su derivación y su integración.
Dominio de definición.
En este caso se trata de determinar los puntos del conjunto
sentido:
EJEMPLO: Ver el ejercicio 1 de la hoja de problemas.
2
n
para los que la función tiene
Introducción a las funciones de varias variables
Representación gráfica.
La representación gráfica estas funciones aporta mucha información sobre las mismas. Sin
embargo sólo es posible en algunos casos de dimensión pequeña. Se han ideado muchas tipos
diferentes de representación pero aquí sólo se ven algunas de las más sencillas.
Para campos escalares de dos variables.
Curvas de nivel.
Dado el campo escalar f :D ⊂ 2 →
de puntos ( x, y ) ∈ D, tales que f ( x, y ) = e .
se define la curva de nivel de valor e al conjunto
NOTAS: 1.- Las curvas de nivel son líneas que están en el dominio de definición D, esto es
en el plano 2 .
EJEMPLO 1: Sea la función f ( x, y ) = 1 − x − y , hallar las curvas de nivel de valor 1, -2 y 5.
2
que cumplen la
Cuando e = 1 la curva de nivel está formada por los puntos de
condición 1 − x − y = 1 . Estos puntos forman una recta de ecuación y = − x . La representación
gráfica de esta recta es:
El resto de las curvas de nivel son 1 − x − y = −2 y 1 − x − y = 5 . Que corresponden,
respectivamente, a las rectas: y = − x + 3 e y = − x − 4 . La representación gráfica de todas
ellas es:
En general, para esta función, la curva de nivel de valor e tiene por ecuación
1 − x − y = e y corresponde a la recta y = − x + 1 − e .
EJEMPLO 2.- Sea el campo escalar dado por z = x 2 + 3 y 2 . Hallar las curvas de nivel
de valor e =1,2 y 3.
En este caso se debe destacar que, por la naturaleza de esta función, no existen curvas
3
Introducción a las funciones de varias variables
de nivel de valor negativo.
2
Para e =1 la curva de nivel está formada por los puntos de
que satisfacen la
2
2
condición x + 3 y = 1 . Estos puntos corresponden a una elipse, centrada en el origen y con
semiejes 1 y 1 / 3 = 0.57735 . La representación gráfica de esta curva de nivel es:
Las demás curvas de nivel son también elipses cuyos semiejes van creciendo a medida
que aumenta el valor e. Así las tres curvas de nivel para los valores e =1, 2 y 3 se representan
en la siguiente gráfica.
Gráfica de la función.
3
La gráfica del campo escalar f ( x, y ) = z está formada por los puntos de
de la forma
( x, y, f ( x, y )) , cuando el punto ( x, y ) pertenece al dominio de definición. En general, si se dan las
condiciones de regularidad suficiente dichos puntos forman una superficie.
EJEMPLO: La gráfica de la función f ( x, y ) = 1 − x − y está formada por los puntos ( x, y, z )
que satisfacen la condición z = 1 − x − y . Estos puntos forman el plano que tiene por ecuación
x + y + z − 1 = 0 . La representación gráfica de dicho plano es:
4
Introducción a las funciones de varias variables
La gráfica de la función z = x 2 + 3y 2 está formada por los puntos de
forma ( x, y, x 2 + 3 y 2 ) , estos puntos forman una figura llamada paraboloide elíptico.
3
de la
NOTA.- La curva de nivel de valor e de una función f ( x, y ) = z se puede interpretar como
proyección, en el plano XY, del corte de su gráfica con el plano z = e . Este hecho suele ser una
indicación muy valiosa para dibujar gráficas.
Trazas.
Las trazas de una función son curvas en el espacio (curvas en
intersección de su gráfica con un plano vertical.
3
) producidas por la
NOTA: Aunque el plano puede ser cualquiera, se suelen utilizar los planos coordenados.
Las trazas suelen ser un buen elemento de ayuda para dibujar la gráfica de una función.
EJEMPLO: Calcular las trazas de la función z = x 2 + 3y 2 con los planos coordenados.
Primero se calcula el corte con el plano XZ en el cual se tiene y = 0 . Sustituyendo
este valor en la ecuación de la función se obtiene: z = x 2 . Esta ecuación es la de una parábola
en el plano XZ, abierta hacia arriba y con vértice en el punto (0,0,0) . Su gráfica es:
Si ahora se calcula el corte con el plano YZ, en el cual se tiene x = 0 , se obtiene que la
traza es la curva z = 3 y 2 , que también es una parábola, con las mismas características de la
anterior, aunque un poco más cerrada, y situada en el plano YZ. Su gráfica es:
5
Introducción a las funciones de varias variables
Dibujando las dos trazas a la vez se puede obtener una idea bastante aproximada de la
gráfica de la función.
Trazado de gráficas.
Utilizando las curvas de nivel y las trazas es posible obtener la información suficiente para
dibujar la gráfica de una función de la forma. z = f ( x, y ) . Para ello es importante tener en cuenta
que las curvas de nivel corresponden a cortes con planos horizontales y las trazas a cortes con
planos verticales.
EJEMPLO: Obtener la gráfica de la función z = x 2 − y 2 .
En primer lugar se calculan las curvas de nivel. En este caso es posible que tengan
valores positivos, negativos e, incluso, el valor 0.
Cuando e > 0 las curvas de nivel tienen por ecuación x 2 − y 2 = e , estás curvas son
hipérbolas simétricas que cortan al eje X en los puntos ( e ,0) y (− e ,0) , en el caso e < 0 ,
las curvas de nivel son también hipérbolas de la forma y 2 − x 2 = −e que cortan al eje Y en
los puntos (0, − e ) y (0,− − e ) , cuando e = 0 , las curvas de nivel tienen por ecuación
x 2 − y 2 = 0 y corresponden a las rectas y = x e y = − x . El aspecto de tales curvas de nivel
es el siguiente:
6
Introducción a las funciones de varias variables
e>0
e=0
e<0
Si ahora se calculan las trazas se encuentra que: El corte con el plano XZ (de ecuación
y = 0 ) es la parábola z = x 2 , esta curva está contenida en el plano XZ, abierta hacia arriba y
tiene como vértice el origen de coordenadas (punto (0,0,0) ). En cambio la traza resultante del
corte con el plano YZ es la curva z = − y 2 , esta parábola está en el plano YZ, abierta hacia
abajo y con vértice también en el punto (0,0,0) . La representación gráfica de esta trazas es la
siguiente:
Entonces, con toda la información obtenida a través de las curvas de nivel y las trazas
se puede concluir que la gráfica de esta función tiene el siguiente aspecto:
Esta superficie pertenece a la familia de las cuádricas y lleva el nombre de paraboloide
hiperbólico. En este ejemplo se trata del caso más sencillo, esto es: simétrico y centrado en el
origen. También es posible referirse a él como el conjunto de puntos que satisfacen la
condición: z − x 2 + y 2 = 0
NOTA: Otras superficies pertenecientes a la familia de las cuádricas, son las siguientes
La esfera: x 2 + y 2 + z 2 = a 2
7
Introducción a las funciones de varias variables
El elipsoide: a 2 x 2 + b 2 y 2 + c 2 z 2 = 1
El paraboloide: z − a 2 x 2 − b 2 y 2 = 0 .
El hiperboloide de una hoja: a 2 x 2 + b 2 y 2 − c 2 z 2 = 1
El hiperboloide de dos hojas: a 2 x 2 + b 2 y 2 − c 2 z 2 = −1
La superficie cónica: z 2 − a 2 x 2 − b 2 y 2 = 0
Para campos escalares de tres variables.
En este caso se trata de campos escalares definidos por funciones de varias variables de la
forma:
3
f :D ⊂
→
Superficies de nivel.
Para obtener información gráfica de estás funciones se definen las superficies de nivel de
valor e como el conjunto de puntos ( x, y, z ) ∈ 3 que satisfacen la condición f ( x, y, z ) = e .
Cuando se dan las condiciones suficientes de regularidad, este conjunto de puntos forman una
3
superficie en
que podría interpretarse como la gráfica del campo escalar de dos variables
definido implícitamente por la condición:
F ( x, y , z ) = f ( x, y , z ) − e = 0 .
Las técnicas para representar estas superficies de nivel son las mismas que las empleadas
para encontrar las gráficas de las funciones reales de dos variables en el apartado anterior.
EJEMPLO: Hallas las superficies de nivel, de valor e = 1, 0 y -1 de la función de tres
variables:
f ( x, y , z ) = x 2 + y 2 − z 2
En primer lugar se toma el valor e = 1 en tal caso la superficie que se obtiene es la
formada por los puntos ( x, y, z ) ∈ 3 que cumplen la condición:
x2 + y 2 − z 2 = 1
Lo primero que se observa, viendo la expresión de la función, es que el origen de
coordenadas (0,0,0) no pertenece a la gráfica. Además la suma de los valores x 2 + y 2 debe
ser siempre mayor o igual a 1. También se puede ver que las curvas de nivel de valor w son
circunferencias de radio 1 + w 2 y que las trazas son las hipérbolas x 2 − z 2 = 1 y y 2 − z 2 = 1 .
Con todos estos datos se puede concluir que esta superficie de nivel tiene la forma:
8
Introducción a las funciones de varias variables
Esta figura recibe el nombre de hiperboloide de una hoja.
La superficie de nivel correspondiente a e = 0 tiene por ecuación x 2 + y 2 − z 2 = 0 que
puede escribirse como:
z 2 = x2 + y2
Mediante razonamientos análogos a los anteriores se llega a la conclusión de que la
superficie de nivel para este valor e = 0 tiene el siguiente aspecto:
Esta figura recibe el nombre de superficie cónica.
Por último, la superficie de nivel correspondiente a e = −1 tiene por ecuación
x 2 + y 2 − z 2 = −1 que puede escribirse como:
z2 − x2 − y2 = 1
Cuya gráfica es:
Que recibe el nombre de hiperboloide de dos hojas.
9