Movimiento Browniano Geométrico

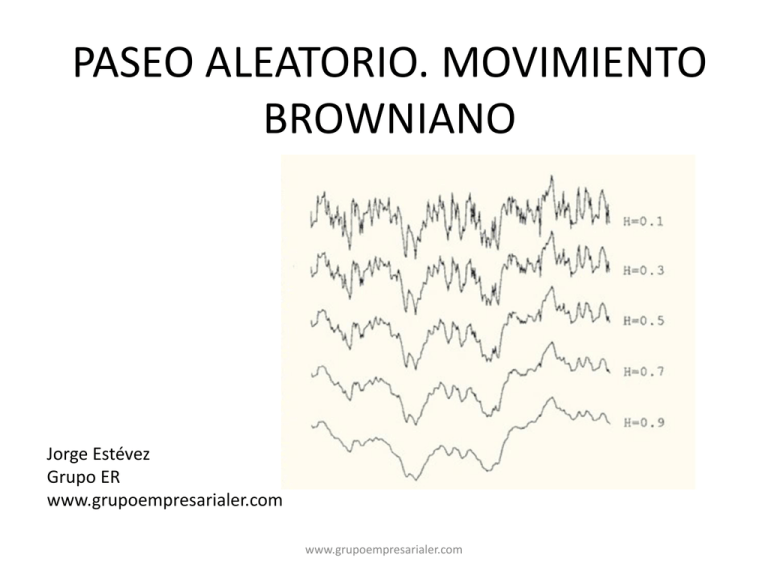
PASEO ALEATORIO. MOVIMIENTO
BROWNIANO
Jorge Estévez
Grupo ER
www.grupoempresarialer.com
www.grupoempresarialer.com
El movimiento browniano es el movimiento aleatorio que se observa en algunas partículas
microscópicas que se hallan en un medio fluido (por ejemplo, polen en una gota de agua).
El movimiento aleatorio de estas partículas se debe a que su superficie es bombardeada
incesantemente por las moléculas (átomos) del fluido sometido a una agitación térmica.
Este bombardeo a escala atómica no es siempre completamente uniforme y sufre
variaciones estadísticas importantes. Así, la presión ejercida sobre los lados puede variar
ligeramente con el tiempo, y así se genera el movimiento observado.
METÁFORA INTUITIVA
Considere un gran balón de 10 metros de diámetro. Imagine este balón en un estadio de
fútbol o cualquier otra área llena de gente. El balón es tan grande que permanece por
encima de la muchedumbre. Las personas aciertan a golpear el balón en diferentes
momentos y direcciones de manera completamente aleatoria. Por ello, el balón no sigue
una trayectoria. Ahora, considere una fuerza ejercida durante un cierto tiempo; podemos
imaginar 20 personas empujando para la derecha y 21 para la izquierda y que cada
persona está ejerciendo cantidades de fuerza equivalentes. En este caso las fuerzas
ejercidas por el lado izquierdo y por el lado derecho no están equilibradas, favoreciendo al
lado izquierdo, por lo que el balón se moverá ligeramente hacia la izquierda. Esta
desproporción siempre existe, y es lo que causa el movimiento aleatorio. Si observáramos
la situación desde arriba, de modo que no pudiéramos ver a las personas, veríamos el
gran balón como un objeto animado por movimientos erráticos.
www.grupoempresarialer.com
EJEMPLO
Para tener una idea del comportamiento de una operativa a través del tiempo.
Simulación de Movimiento Brownianos geométricos para calcular las probabilidades de
pérdida después de un tiempo T. Operativa tanto de series temporales independientes o
correlacionadas.
Precios siguen el GBM (Movimiento Browniano geométrico), cuyos parámetros de drift y
volatilidad los podemos estimar, por ejemplo, a partir de datos históricos y luego se
calcula la probabilidad de que el balance caiga más de un (1-p)%..
VEAMOS
S(t) es el precio simulado
dS es el incremento del precio simulado
r es el tipo interés sin riesgo o deriva del proceso
dt es el salto de tiempo al que se simula
σ es la volatilidad del activo.
dWt es un movimiento browniano o parte aleatoria del proceso.
En esta ecuación, un incremento del valor de S es igual a la suma de la tendencia más la
variabilidad.
www.grupoempresarialer.com
El valor de una operativa (spread por ejemplo) es una variable aleatoria.
Queremos tener una idea de la volatilidad del spread.
Usualmente se toman los precios diarios, se calculan los rendimientos diarios y
en base a ellos la desviación típica.
La desviación típica (raíz cuadrada de la varianza) es un estimador de la
volatilidad.
Al suponer que la volatilidad histórica es una buena estimación de la volatilidad
futura estaremos confundiendo estimador con predictor.
Supongamos que decidimos entrar porque estimamos que tenía una
rentabilidad esperada del 10% y volatilidad 25%.
Supongamos que disponemos de un histórico con la evolución de los precios.
www.grupoempresarialer.com
Simulamos 100 trayectorias de evolución utilizando Monte Carlo.
Supongamos que el precio actual del spread es de 18 (en divisa)
Cada línea representa una posible trayectoria del activo a partir de los 18
Algunas suben a 40
Otras bajan a 8
Podemos perder hasta 10
www.grupoempresarialer.com
Simulamos otras 100 trayectorias de evolución utilizando Monte Carlo suponiendo que
ahora la volatilidad es del 30%.
Podemos valorar el efecto del aumento en la volatilidad observando las posibles
trayectorias y comparando
www.grupoempresarialer.com
ALGUNOS TIPO DE MOVIMIENTOS BROWNIANOS
Movimiento Browniano con deriva ( o Movimiento Browniano Aritmético)
www.grupoempresarialer.com
Movimiento Browniano Geométrico
Se trata del proceso estocástico que resuelve el modelo de precios de activos …
financieros
propuesto por Black, Scholes y Merton .
Xt = exp(Bt + t); t > 0
siendo > 0 (volatilidad) y 2 R (deriva) constantes
www.grupoempresarialer.com
Movimiento Browniano con reversión a lamedia ( o de Ornstein-Uhlenbeck)
www.grupoempresarialer.com
EXPONENTE DE HURST
La desviación del precio es
directamente proporcional a la raíz
cuadrada del tiempo.
Cuando más grande sea ese
exponente, querrá decir que
en el grafico predominan más
las tendencias
www.grupoempresarialer.com