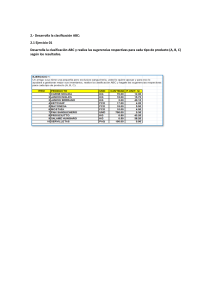
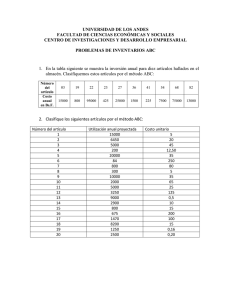
Problema 125. Si a, b, c son estrictamente positivos, demostrar que
Anuncio

Problema 125. Si a, b, c son estrictamente positivos, demostrar que r abc(a2 b + b2 c + c2 a) 1 abc ≤ ≤ (a2 b + b2 c + c2 a) 3 3 Solución: Si tomamos las dos desigualdades por separado, después de elevarlas al cuadrado y simplificar llegaremos a la misma desigualdad: 1 abc ≤ (a2 b + b2 c + c2 a) 3 Ésta es la que vamos a probar. Dado que a, b, c son estrictamente positivos, nada nos impide considerar las tres cantidades a c b , , . c b a Aplicando la desigualdad aritmético-geométrica a estas tres cantidades, obtenemos: r c b a + + c b 3 a c b a ≥ · · =⇒ 3 c b a 2 2 2 1 a b+b c+c a ≥ 1 =⇒ abc ≤ (a2 b + b2 c + c2 a) =⇒ 3abc 3 lo cual termina el problema. 1 Revista Escolar de la Olimpíada Iberoamericana de Matemática http://www.campus-oei.org/oim/revistaoim/ Edita: