practico 5

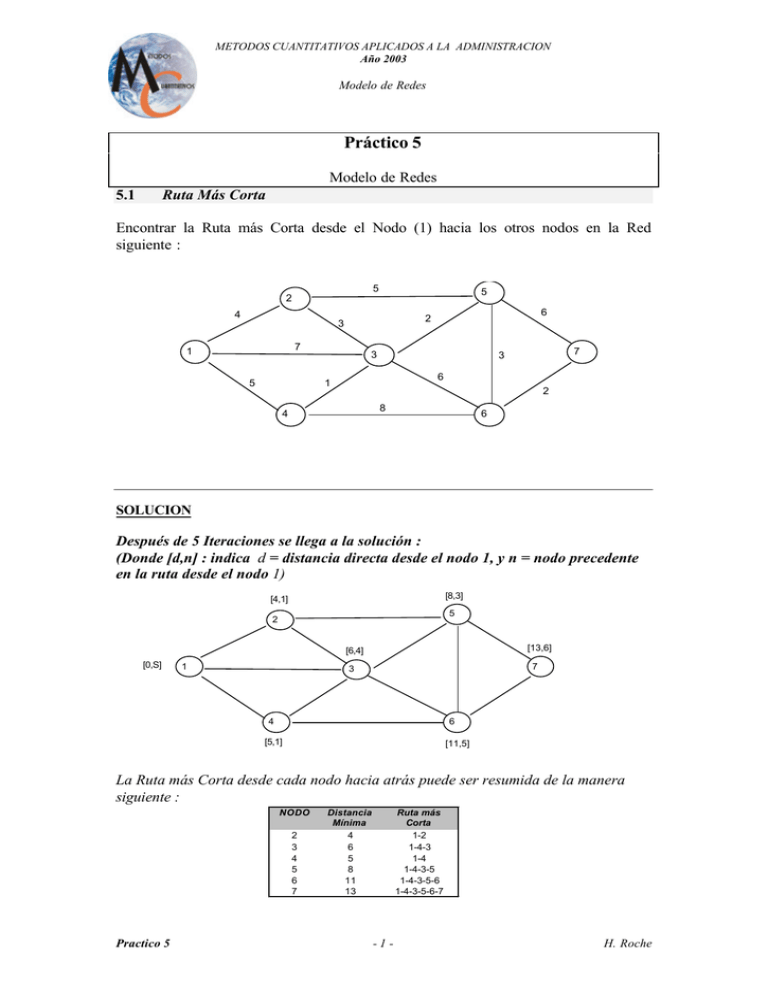
METODOS CUANTITATIVOS APLICADOS A LA ADMINISTRACION
Año 2003
Modelo de Redes
Práctico 5
Modelo de Redes
5.1
Ruta Más Corta
Encontrar la Ruta más Corta desde el Nodo (1) hacia los otros nodos en la Red
siguiente :
5
5
2
4
7
1
5
6
2
3
3
7
3
6
1
2
8
4
6
SOLUCION
Después de 5 Iteraciones se llega a la solución :
(Donde [d,n] : indica d = distancia directa desde el nodo 1, y n = nodo precedente
en la ruta desde el nodo 1)
[8,3]
[4,1]
5
2
[13,6]
[6,4]
[0,S]
1
7
3
4
6
[5,1]
[11,5]
La Ruta más Corta desde cada nodo hacia atrás puede ser resumida de la manera
siguiente :
NODO
2
3
4
5
6
7
Practico 5
Distancia
Mínima
4
6
5
8
11
13
Ruta más
Corta
1-2
1-4-3
1-4
1-4-3-5
1-4-3-5-6
1-4-3-5-6-7
-1 -
H. Roche
METODOS CUANTITATIVOS APLICADOS A LA ADMINISTRACION
Año 2003
Modelo de Redes
5.2
Ruta Más Corta
Una persona X debe estar en la ciudad (6) para un evento de la empresa en la
noche del mismo día. Tiene varias rutas alternativas para llegar a (6)
F
2
A
5
L
B
K
G
1
6
C
D
E
J
3
I
H
M
4
saliendo de (1). La Red siguiente resume las rutas alternativas.
La Tabla siguiente indica el modo de transporte, el tiempo de viaje, y el costo
Ruta
A
B
C
D
E
F
G
H
I
J
K
L
M
Modo de
Transporte
tren
avión
taxi
omnibus
tren
omnibus
omnibus
taxi
tren
omnibus
taxi
tren
omnibus
Tiempo
(horas)
4
1
6
2
3.333
3
4.667
1
2.333
6.333
3.333
1.333
4.667
Boleto
20
115
90
10
30
15
20
15
15
25
50
10
20
asociado en cada una de las ramas de la red.
Si esa persona X gana una salario de $15 por hora, ¿cual será la ruta que
deberá escoger para minimizar el costo total de viaje?
Se Pide
1. Determinar los costos asociados a cada Arco.
Costo del Arco = $15x
60
2
+ Costo del Viaje
80
1
Tiempo de Viaje(en horas)
5
30
130
100
90
180
6
40
80
120
3
50
30
90
4
Practico 5
-2 -
H. Roche
METODOS CUANTITATIVOS APLICADOS A LA ADMINISTRACION
Año 2003
Modelo de Redes
2. El Costo Mínimo es $150. La ruta de mínimo costo es 1-3-4-5-6.
[120,4]
[80,1]
60
2
30
80
[0,S]
5
130
1
100
90
180
6
[40,1]
40
[150,5]
120
3
80
50
30
90
4
(70,3)
5.3
Arbol de Expansión Mínima
Encontrar el Arbol de Expansión Mínimo en la Red siguiente .
60
3
45
20
50
1
9
30
45
6
4
40
35
40
5
30
15
25
10
20
35
7
30
2
25
8
50
SOLUCION
60
3
45
20
50
1
45
6
4
40
35
40
5
30
15
25
10
20
35
7
30
2
50
Practico 5
9
30
-3 -
25
8
H. Roche
METODOS CUANTITATIVOS APLICADOS A LA ADMINISTRACION
Año 2003
Modelo de Redes
5.4
Ejemplo- Modelo de Flujo Máximo (Aguas del Estado)
La empresa “Aguas del Estado” cuenta con una red de cañerías muy
heterogénea en cuanto a años de servicio, y quiere llevar agua del barrio A al
barrio G, abasteciendo en el camino a todos los demás. Pretende que el
caudal medido en decenas de litros por segundo sea máximo, pero debido a la
edad avanzada de algunos tramos debió confeccionar un croquis de la ciudad
en el cual consta el flujo máximo que soporta cada tramo. El mismo se
muestra a continuación:
2
0
0
B
2
7
8
0
0
0
6
A
E
0
0
D
5
3
G
2
4
0
2
0
0
C
0
F
5
5
0
Se pide:
a) Identifique el flujo máximo a asignar en total y en cada tramo, usando el
algoritmo de trayectorias aumentadas, de modo tal que la solución sea óptima.
b) Verifique el resultado obtenido por medio del teorema del flujo máximo –
2
cortadura mínima.
0 E
8
0
B
0
2
SOLUCIÓN
7
4 ==>
0
0
6
A
0
3
0
D
5
G
4
0
4
2
0
B
7
1
2
8
0
0
0
5
E
0
2
A
1
F
1
0
2
0
C
4
5 = 4 + 1 ==>
D
5
G
5
1
F
0
0
B
E
5
2
7
6
2
3
0
5
0
0
0
5
2
0
2
0
C
4
A
D
0
G
==> 10 = 4 + 1 + 5
2
0
5
1
4
Practico 5
==> 5 = 4 + 1
2
0
10 = 4 + 1 + 5 ==>
==> 4
2
0
2
0
C
F
0
0
5
-4 -
H. Roche
METODOS CUANTITATIVOS APLICADOS A LA ADMINISTRACION
Año 2003
Modelo de Redes
0
2
2
B
2
5
12 = 4 + 1 + 5 + 2 ==>
1
0
7
0
0
A
E
5
6
2
D
0
G
==> 12 = 4 + 1 + 5 + 2
2
0
5
2
1
0
C
4
5
0
3
2
B
4
13 = 4 + 1 + 5 + 2 +1 ==>
E
0
5
1
1
8
1
0
A
0
F
0
6
D
2
0
G
1
0
==> 13 = 4 + 1 + 5 + 2 + 1
5
1
1
4
El Cuadro
Problema.
1
C
F
0
y el Diagrama de Flujos Netos siguiente resumen la solución del
Tr [1]
A-B
A-C
A-D
B-D
B-E
C-D
C-F
D-E
D-F
E-F
E-G
F-G
Flujo
Tr [2]
Tr [3]
Tr [4]
Tr [5]
2
1
1
5
1
2
-1
1
4
5
4
4
1
1
5
2
1
-1
1
5
2
1
2
3
6
A
E
8
5
1
D
G
1
==> 13
1
1
4
5
C
Practico 5
Flujo
Neto
3
4
6
1
2
-1
5
5
1
-1
8
5
13
4
B
13 ==>
0
5
5
-5 -
F
H. Roche
METODOS CUANTITATIVOS APLICADOS A LA ADMINISTRACION
Año 2003
Modelo de Redes
5.5
Modelo de Flujo Máximo
En la ciudad X, el tránsito está muy congestionado. Existen avenidas que conectan
diversos puntos de la ciudad. En el siguiente Gráfico se muestra el número promedio
de vehículos que circulan por minuto por cada avenida, y las capacidades adicionales
de circulación en cada una de ellas.
B
20
15
8
10
9
A
5
7
8
5
C
E
12
12
6
4
28
17
D
15
SE PIDE:
-
En base a la información disponible a partir del Gráfico responder a las siguientes
preguntas y justificar sus respuestas.
(a)
Qué avenida tiene más capacidad de circulación?
Capacidad
residual
10
A
Cantidad
de flujo
asignado
20
B
Capacidad de circulación = Capacidad de arco
AB=30
BE=20
AC=17
CE=24
AD=22
DE=21
BC=15
CD=32 es el arco de mayor capacidad de circulación
(b)
Practico 5
¿Qué avenida está más próxima a colapsar debido al embotellamiento?
Aquella que tiene menor capacidad residual, la avenida CD => 4
vehículos por minuto
-6 -
H. Roche
METODOS CUANTITATIVOS APLICADOS A LA ADMINISTRACION
Año 2003
Modelo de Redes
(c)
Qué ruta(s) entre A y E está(n) próxima(s) a colapsar debido al
embotellamiento?
Capacidad mínima residual = Capacidad residual de la trayectoria
Entonces busco el arco (avenida) de menor capacidad residual (CD) y
todas las rutas que pasen por esa avenida estarán próximas a colapsar.
(d)
Cuántos vehículos podrán circular como máximo en promedio por
minuto, entre A y E?
Flujo Máximo/Cortadura Mínima
DE + CE + BE = 21+24+20 = 65
5.6
Modelo de Flujo Máximo
Una empresa maneja una flota de avionetas y se dedica a la distribución de paquetes
y correspondencia comercial entre las siguientes ciudades : SC, BA, MVD, LP, AS
y SP.
La empresa está interesada en conocer cual es la carga máxima que puede transportar
en un día indirectamente entre SC (1) y SP (6) ( via LP, AS, MVD, y/o BA), en el
caso de que los vuelos directos SC-SP se cancelaran.
Las rutas indirectas entre SC y SP están indicadas en el diagrama siguiente,
incluyendo las estimaciones de capacidad de transporte adicional (medida en términos
de metros cúbicos por día).
LP
As
4
12
2
3
8
20
14
8
16
8
10
1
SC
15
25
6
7
11
18
9
10
17
15
6
SP
3
Mvd
20
6
4
4
14
5
BA
SE PIDE :
(A)
Definir el concepto de Cortadura y como calcular el valor de una Cortadura?
Cortadura: cualquier conjunto de arcos dirigidos que contienen al menos un
arco de cada trayectoria dirigida que va del nodo origen al nodo destino.
Valor de una Cortadura: suma de las capacidades de los arcos.
Practico 5
-7 -
H. Roche
METODOS CUANTITATIVOS APLICADOS A LA ADMINISTRACION
Año 2003
Modelo de Redes
(B)
(C)
(D)
Que establece el Teorema de Flujo-máximo Cortadura-Mínima?
Teorema de Flujo Máximo Cortadura Mínima : aquel que indica que para
cualquier red con un solo nodo origen y un solo nodo destino, el flujo máximo
factible del origen al destino es igual al valor mínimo de todas las cortaduras
de la red.
Existe suficiente capacidad adicional para transportar en un día indirectamente
50 metros cúbicos de carga entre SC y SP?
Capacidad adicional = 10 + 15 +7 +18 = 50 m3
Cual es la carga máxima que la firma puede transportar y cual ruta emplear ?
Carga máxima => cortadura mínima => 3-6 + 4-6 + 5-6 = 41 + 32 + 17 = 90
m3
Ruta a emplear :
Trayectoria
1-2-3-6
1-3-6
1-4-6
1-5-4-6
1-5-6
1-2-5-3-6
1-2-5-6
TOTAL
5.7
Capacidad mínima
16
23
18
14
8
2
9
90
Modelo de Flujo Máximo
Encontrar el Flujo Máximo desde el nodo (1) al nodo (7) en la Red siguiente .
4
1
3
2
0
3
2
5
2
4
0
0 7
0
3 3
3
0 4
5
1
4
3
0
5
1
3
3
0
6
6
Cortadura Mínima = 10
Cortadura = 11
SOLUCION
Trayectoria de aumento
1
2
3
4
5
Practico 5
1-2-5-7
1-4-7
1-3-4-6-7
1-3-6-7
1-2-4-3-6-7
-8 -
Capacidad de
Flujo Asignado
2
3
1
2
2
H. Roche
METODOS CUANTITATIVOS APLICADOS A LA ADMINISTRACION
Año 2003
Modelo de Redes
0
1
1
2
4
5
0
4
3
4
2
4
3
1
3
Practico 5
5
2
1
1
4
Trayectorias de Aumento
2
3
4
1
10
3
4
3
2
0
6
2
10
TOTAL
2
3 7
5
2
2
2
1
2
0
5 3
3 4
0
4
0
1
0
3
ARCOS
1-2
1-3
1-4
2-5
2-4
3-4
3-6
4-6
4-5
4-7
5-7
6-7
5
4
7
5
6
5
2
Flujo Máximo
(1) --> (7)
2
3
2
2
2
-2
2
1
2
2
1
2
2
1
1
3
2
3
-9 -
Flujo
Neto
4
3
3
2
2
-1
4
1
0
3
2
5
10
H. Roche