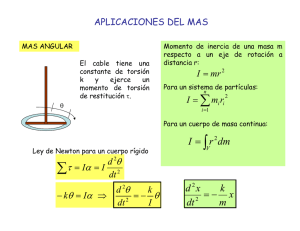
PENDULO: Simple, Compuesto, Cónico y de Torsión

E - PENDULO: Simple, Compuesto, Cónico y de Torsión
Los fundamentos teóricos de los péndulos simple y compuesto ya se han
sido brindados en los Fundamentos Teóricos. Por lo que aquí se tratarán solamente
las características del péndulo cónico y de torsión
O
α
PÉNDULO CÓNICO
Un péndulo cónico consiste en una masa m, que gira
alrededor de la vertical con velocidad angular w, colgada
F
al extremo de un hilo de longitud L. De las figuras
vemos que la fuerza centrípeta (Fn) necesaria es
v
C Fn
proporcionada por la componente horizontal de la
tensión en la cuerda (F). La componente vertical es
R
α
igual al peso de la masa (W) que gira. Así,
m v2
FN = F sen α =
= m w2R = m w2L sen α
W=mg
R
F
w 2 L sen α
v2
Vemos de la figura: tg α = N =
=
W
g
Rg
senα
g
⇒ cos α = 2
o, ya que la
tg α =
cos α
w L
Cuanto mayor es la velocidad angular w, mayor es el ángulo α , como se
demuestra experimentalmente. Por esta razón el péndulo cónico ha sido utilizado como
un regulador de velocidad de las máquinas de vapor; cierra la válvula de la entrada de
vapor cuando la velocidad supera un límite prefijado y la abre cuando dicha velocidad
baja de dicho límite.
θ
L
T cos θ
h
T
R
T
θ
T sen θ
W=mg
W=mg
Al aumentar el ángulo, la posición vertical de la masa se eleva,
originando una reducción en la distancia h por debajo del punto de soporte. Si
deseamos expresar la ecuación de la tangente en términos de la posición vertical
tenemos:
R
Tan θ =
h
R
v2
de donde obtenemos
=
gR
h
87
Por lo tanto la distancia del peso por debajo del soporte es una función de
la velocidad lineal y está dada por
h=
gR 2
v2
Este principio se aplica a los reguladores de algunas máquinas.
posición del peso se puede utilizar para abrir o cerrar válvulas de combustible.
La
Una forma más útil de la ecuación se puede obtener expresando la
velocidad lineal en términos de la frecuencia rotacional. Puesto que v = 2 Π f R, se
puede escribir:
g R2
g
h=
4 Π2 R2 f
2
=
4 Π2 f
2
Despejando f se obtiene:
f =
1
2Π
g
h
PÉNDULO DE TORSIÓN
O
Otro ejemplo de movimiento armónico simple es el
péndulo de torsión, consistente en un cuerpo
suspendido por un alambre o fibra (como se muestra
C
en la figura) de tal manera que la línea OC pasa por el
centro de masa del cuerpo. Cuando el cuerpo rota un
θ
ángulo θ a partir de su posición de equilibrio, el
alambre se tuerce, ejerciendo sobre el cuerpo un
torque τ alrededor de OC que se opone al
desplazamiento θ y de magnitud proporcional al
ángulo τ = - k θ donde k es el coeficiente de torsión del alambre.
Si I es el momento de inercia del cuerpo con respecto al eje OC, la ecuación del
movimiento, usando la ecuación:
dw
= τ OC
dt
d 2θ
I 2 =-kθ
dt
I
y con α = d2 θ / dt2, se tiene:
ó
d 2θ
k
+
θ =0
2
I
dt
ésta es la ecuación diferencial del movimiento armónico simple, con w2 = k/I, el período
de oscilación es:
I
P=2 Π
k
Este resultado es útil experimentalmente para determinar el momento de
inercia de un cuerpo suspendiéndolo de un alambre cuyo coeficiente de torsión k se
conoce, y luego midiendo el período P de oscilación.
88