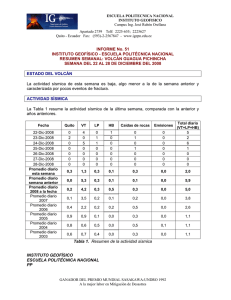
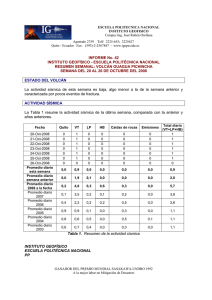
ELEMENTOS DE PROSPECCIÓN SÍSMICA – Alfonso Muñoz Martín

ELEMENTOS DE PROSPECCIÓN SÍSMICA – Alfonso Muñoz Martín
1. - INTRODUCCIÓN
En la prospección sísmica, las ondas sísmicas se propagan hacia el interior de la tierra y se
miden los tiempos de viaje de las ondas que regresan a la superficie después de sufrir refracción o
reflexión en límites geológicos presentes en el subsuelo. Estos tiempos de viaje se pueden convertir
en profundidades e, incluso, se puede cartografiar sistemáticamente la distribución en profundidad de
las superficies de interés geológico.
La prospección sísmica se comenzó a realizar en los primeros años 20. Representó un
desarrollo natural de los métodos sismológicos de los terremotos, establecidos ya desde hacía
mucho tiempo, en los cuales los tiempos de viaje de las ondas producidas en los terremotos se
registraban en observatorios simológicos, y eran utilizadas para deducir información de la estructura
interna de la tierra. La sismología proporciona información sobre las principales capas de la tierra, y
la medida de la velocidad de las ondas de los terremotos a través de las diferentes capas
proporciona importantes pistas sobre su composición y constitución. Del mismo modo, pero a una
escala mucho menor, la prospección sísmica proporciona una clara, e incluso una detallada imagen
de la geología subsuperficial. Esta herramienta indudablemente representa el método de prospección
geofísica más importante, tanto en términos de la cantidad de actividad prospectiva, como en el
amplio rango de sus aplicaciones.
Muchos de los principios de la sismología son aplicables a la prospección sísmica. Sin
embargo, esta última solamente se ocupa de la estructura del subsuelo hasta una profundidad de
varios kilómetros como máximo, y utiliza fuentes sísmicas artificiales como explosiones, cuyas
características de localización, ocurrencia y tipos de fuente están bajo el control directo del
geofísico, lo que no ocurre con los terremotos. La prospección sísmica también utiliza sistemas de
registro y técnicas de procesado e interpretación de los datos especializadas.
Los métodos sísmicos de prospección se aplican ampliamente a problemas de exploración
que involucran la detección y cartografía de límites subsuperficiales de geometría normalmente
simple. Los métodos son particularmente bien adecuados para la cartografía de secuencias
sedimentarias estratificadas, y por lo tanto, se aplican ampliamente en la búsqueda de petróleo y gas.
Los métodos están tan bien muy indicados en una escala menor, para la cartografía de capas
sedimentarias cercanas a la superficie, del nivel piezométrico y, en un contexto ingeniero,
investigaciones locales incluyendo la profundidad de los niveles rocosos. La prospección sísmica se
puede desarrollar en tierra o en mar, y se usa de un modo muy extensivo en prospección geológica
en el mar para la exploración de recursos situados bajo el mar.
En este capítulo se revisan los principios físicos en los que se basan los métodos sísmico un
nivel elemental, comenzando con una discusión sobre la naturaleza de las ondas sísmicas y
continuando sobre su modo de propagarse en el interior de la tierra, con especial referencia a la
reflexión y refracción en las superficies situadas entre diferentes tipos de rocas. Para entender los
diferentes tipos de ondas sísmicas que se propagan a través del subsuelo lejos de una fuente sísmica,
es necesario considerar algunos conceptos elementales sobre el esfuerzo y la deformación.
2. - ESFUERZO Y DEFORMACIÓN
Cuando se aplican fuerzas externas a un cuerpo, se establecen dentro de el unas fuerzas
internas equilibradas. El esfue rzo es una medida de la intensidad de estas fuerzas internas
equilibradas. El esfuerzo, que actúa sobre cualquier área de cualquier superficie dentro del cuerpo,
se puede resolver en una componente normal de esfuerzo perpendicular a la superficie, y una
componente tangencial o de cizalla en el plano de la superficie.
En cualquier punto en un cuerpo sometido a esfuerzos, se pueden definir tres planos
ortogonales, en los cuales las componentes del esfuerzo son principalmente esfuerzos normales, es
decir, sin esfuerzos de cizalla actuando sobre ellos. Estos planos definen tres ejes ortogonales
conocidos como los ejes principales de esfuerzo, y los esfuerzos normales que actúan en esas
direcciones se conocen como esfuerzos principales. Cada uno de los esfuerzos principales
representa un equilibrio de las componentes de la fuerza de igual magnitud, pero de sentido
contrario. Se denomina esfuerzo compresivo cuando las fuerzas están dirigidas cada una hacia la
otra (hacia el interior), y esfuerzo extensivo si se dirigen en contra (hacia fuera).
Esfuerzo (σ)
Si los esfuerzos principales son de igual magnitud en un cuerpo, este estado de esfuerzos se
denomina hidrostático, debido a que es el estado de esfuerzo a través de un fluido en reposo. No
existen esfuerzos de cizalla en un campo de esfuerzos hidrostático, debido a que éstos no pueden se
sostenidos por un cuerpo fluido. Si los esfuerzos principales son diferentes, aparecen esfuerzos de
cizalla a lo largo de todas superficies del interior del cuerpo, excepto en aquellas perpendiculares a
los ejes principales.
Un cuerpo sujeto a esfuerzo sufre un cambio de forma y/o tamaño denominado
deformación. Hasta un cierto límite de esfuerzo, conocido como resistencia elástica de un material
(yield strength), la deformación se relaciona de un modo lineal con el esfuerzo aplicado y se
denomina elástica (Ley de Hooke). Esta deformación elástica es reversible, por lo que cuando se
deja de aplicar el esfuerzo la
deformación desaparece. Si la
resistencia elástica de un cuerpo es
Rango
superada, la deformación comienza a
Elástico
no ser lineal, y parcialmente irreversible
Deformación Plástica
(produce deformación permanente), y
Rango
pasa a ser conocido como
Lineal
Rotura
deformación plástica o dúctil. Si el
esfuerzo aumenta aún más, se produce
Límite
Elástico
la fractura del cuerpo. Un ejemplo de
curva esfuerzo / deformación aparece
Límite de
en la figura 2.1.
Proporcionalidad
La relación lineal entre el
Def. permanente
esfuerzo y la deformación en el campo
elástico es específica para cada
Deformación (ε)
material por medio de su módulo de
elasticidad, que expresa la razón entre Figura 2.1: Ejemplo de una típica curva de esfuerzo un tipo de esfuerzo particular con la deformación para un cuerpo sólido.
deformación resultante.
Consideremos una varilla, de longitud original l y sección A, que se extiende un incremento
de longitud (∆l) debido a la aplicación de una fuerza tensional (F) en ambas caras (figura 2.2a). El
módulo de elasticidad relevante es el denominado Módulo de Young (E), definido por:
F
Esfuerzo longitudinal
Modulo de Young E =
= A
Deformacion longitudinal ∆l
l
Nótese que la extensión de esta varilla se acompañará de una reducción de su diámetro (la
varilla sufre deformación tanto longitudinal como lateral). La razón entre la deformación lateral y
longitudinal es conocida como el coeficiente de Poisson (σ), y suele tener valores próximos a
0.25.
El módulo de compresibilidad (K) expresa la razón entre el esfuerzo y la deformación para
el caso de una presión hidrostática simple (P) aplicada a un elemento cúbico (figura 3.2.2b), y se
define como:
esfuerzo hidrostatico
P
Modulo de Compresibilidad K =
=
deformacion de volumen ∆v
v
De un modo similar el módulo de cizalla (µ) se define como la razón entre el esfuerzo de
cizalla (τ) y la deformación de cizalla resultante (tan θ):
τ
( Modulo de cizalla) µ =
tan θ
Finalmente, el módulo axial (ψ) define la razón del esfuerzo longitudinal y la deformación
longitudinal para el caso de que no hay deformación lateral (el material está constreñido a
deformarse de un modo uniaxial):
F
Esfuerzo Longitudinal
( Modulo Axial ) ψ =
= A
Deformacion Longitudinal ( uniaxial ) ∆l
l
A
τ
C
x+ ∆ x
F
θ
F
x
B
∆y/2
∆x
y
Fx
P
D
P
x
P
Figura 2.2: Representación gráfica de los módulos elásticos. a) Módulo de Young (E); b) Módulo de
compresibilidad (K); c) Módulo de Cizalla (µ) y d) Módulo Axial ( ψ).
3. - LAS ONDAS SÍSMICAS
Las ondas sísmicas son parcelas de energía de deformación elástica que se propagan desde
una fuente sísmica (como un terremoto o una explosión) hacia fuera. Las fuentes sísmicas apropiadas
para la prospección sísmica son aquellas que generan trenes de onda de corta vida conocidos como
pulsos), que típicamente contienen un amplio rango de frecuencias. Las deformaciones asociadas
con el paso de un pulso sísmico se pueden considerar elásticas, excepto en la zona inmediata a la
fuente. Con esta asunción, las velocidades de propagación de los pulsos sísmicos están
determinados por los módulos elásticos y las densidades de los materiales a través de los que pasan.
Existen dos tipos fundamentales de ondas sísmicas: ondas internas o de volumen (body waves) y
ondas de superficie (surface waves).
La velocidad de propagación de una onda interna o de volumen e cualquier material viene
dada por:
V=
mod ulo elastico apropiado del material
densidad del material
de este modo, la velocidad de las ondas P (VP) de las ondas internas compresivas, que
involucran deformación compresiva, viene dada por:
ψ
VP =
ρ
y dado que ψ = K + 4 3 ⋅ µ , VP pasa a ser:
VP =
K + 43 ⋅ µ
ρ
y la velocidad de las ondas S (ondas de cizalla), que involucran deformación de cizalla pura, viene
dada por:
µ
VS =
ρ
Puede deducirse de estas ecuaciones que las ondas compresivas siempre viajan más rápido
que las ondas S en el mismo medio. La relación entre VP y VS en cualquier material es función
únicamente por el valor del coeficiente de Poisson (σ) para ese material:
VP
=
VS
2 ⋅ (1 − σ )
(1 − 2 ⋅ σ )
y como el coeficiente de Poisson para las rocas consolidadas es típicamente 0.25,
VP ≈ 1.7 ⋅ VS
4 - VELOCIDADES DE ONDAS COMPRESIVAS DE LAS ROCAS
Debido a su variada composición, texturas (forma del grano y grado de empaquetado),
porosidades y contenido de fluidos en los poros, las rocas varían en su módulo elástico y densidades
e, incluso, en sus velocidades sísmicas. La información sobre la velocidad de las ondas compresivas
(Vp) de las capas de rocas que proporciona la prospección sísmica es importante por dos razones:
1) Es necesaria para la conversión de los tiempos de viaje de las ondas sísmicas en
profundidades.
2) Proporciona información sobre la litología, o, incluso, la naturaleza del fluido contenido en
el interior de los poros.
Las velocidades de las rocas se pueden medir in situ, mediante medidas de campo, o bien en
el laboratorio, usando muestras de roca convenientemente preparadas. En el campo, la prospección
sísmica produce estimaciones de la velocidad para las casa de roca definidas por superficies de
reflexión o de refracción, tal y como se discute en los capítulos 4 y 5.
Si existen sondeos en las proximidades de una zona de prospección sísmica, puede ser
posible correlacionar los valores de velocidad con las unidades litológicas encontradas a lo largo de
los sondeos.
5 - ATENUACIÓN DE LA ENERGÍA SÍSMICA A LO LARGO DE LA TRAYECTORIA
DE LOS RAYOS
Cuando se propaga un impulso sísmico, la energía original E, que se transmite hacia el
exterior de la fuente, comienza a distribuirse sobre una esfera cuyo radio va aumentando. Si el radio
de la esfera es r, la cantidad de energía contenida dentro de una unidad de área de dicha esfera es:
E
4⋅π ⋅ r2
Por lo tanto, la energía contenida en el rayo va disminuyendo a lo largo del mismo en función
de r , debido al efecto de la expansión geométrica. Dado que la amplitud de la onda dentro de un
material homogéneo es proporcional al la raíz cuadrada de la energía de la onda, la amplitud
disminuye en función de r-1.
-2
Otra causa de pérdida de energía a lo largo de la trayectoria del rayo se debe a que el medio
no es perfectamente elástico en su respuesta de paso de las ondas sísmicas. La energía elástica va
siendo gradualmente absorbida por el medio por pérdidas friccionales internas, lo que conduce
eventualmente a la total desaparición de la perturbación sísmica. El coeficiente de absorción (α )
expresa la proporción de pérdida de energía durante la transmisión a través de una distancia
equivalente una longitud de onda completa (λ). Los valores de α para los materiales comunes en la
tierra varían de 0.25 a 0.75 dB⋅λ-1.
Dentro del rango de frecuencias utilizadas
en prospección sísmica, se asume que el
coeficiente de absorción es independiente de la
frecuencia. Si la cantidad de absorción por longitud
de onda es constante, se deduce que las
frecuencias más altas se atenúan más rápidamente
que las bajas frecuencias en función del tiempo o la
distancia.
Para ilustrar este hecho consideremos dos
ondas con frecuencias de 10 Hz y 100 Hz que se
propagan por una roca con una Vp = 2 Km /s y un
α = 0.5 dB/λ. La onda de 100 Hz (λ=20 m) se
atenuará debido a la absorción por 5 dB sobre una
distancia de 200 m, mientras que la onda de 10 Hz
(λ=200 m) se atenuará sólo 0.5 dB sobre la misma
distancia. La forma de un pulso sísmico con un
contenido de frecuencias amplio cambia
Figura 5.1: Cambio de forma progresivo de un pico continuamente durante su propagación debido a la
de un pulso durante su propagación a través del
progresiva pérdida de las frecuencias más altas. En
interior de la tierra debido a los efectos de la
general, el efecto de la absorción es producir un
absorción.
alargamiento progresivo del pulso sísmico.
6 - TRAYECTORIAS DE LOS RAYOS SÍSMICOS EN MEDIOS ESTRATIFICADOS
En una superficie situada entre dos capas de roca, generalmente se produce un cambio de la
velocidad de propagación debido a las diferencias en las propiedades físicas de las dos capas. En
esta superficie la energía contenida en un pulso sísmico incidente se divide en un pulso transmitido y
otro reflejado. Las amplitudes relativas de los pulsos transmitidos y reflejados, en términos de las
velocidades y densidades de los dos medios, vienen dadas por las ecuaciones de Zoeppritz (Telford
et al., 1976).
6.1 Reflexión y Transmisión de los Rayos Sísmicos Incidentes Normales
Consideremos un rayo compresivo de Amplitud A0, que incide normalmente en una
superficie situada entre dos medios con diferente velocidad y densidad (Figura 6.1). Un rayo
transmitido de Amplitud A2 viaja a través de la superficie en la misma dirección del rayo incidente, y
un rayo reflejado de Amplitud A1 vuelve a lo largo de la trayectoria del rayo incidente.
La energía total de los rayos transmitidos y reflejados debe ser igual a la energía del rayo
incidente. Las proporciones relativas de la energía transmitida y reflejada se determinan por el
contraste en el valor de la Impedancia Acústica (Z) a través de la superficie. La Impedancia
Acústica de una roca es el producto de su densidad y de su velocidad de las ondas compresivas
(Vp):
Z = ρ ⋅ Vp
A0
A1
V1, ρ1
Aunque resulta difícil relacionar
la impedancia acústica con una
propiedad tangible de las rocas, en
general se puede decir que cuanto más
resistente sea una roca, mayor será su
impedancia acústica.
La impedancia acústica es un
análogo muy próximo a la Impedancia
V1, ρ 1 = V2, ρ 2
eléctrica, y, así como la máxima
transmisión de energía eléctrica requiere
V2, ρ 2
un ajuste de impedancias eléctricas, la
A2
máxima transmisión de energía sísmica
requiere un buen ajuste de impedancias
acústicas. de este modo cuanto menor
sea el contraste en el valor de
Figura 6.1:Transmisión y reflexión de un rayo perpendicular a Impedancia Acústica a través de una
interfase, mayor será la proporción de
una superficie con contraste de impedancia acústica (Z).
energía transmitida a través de esa
interfase.
El coeficiente de reflexión (R) es la razón entre la Amplitud A1 del rayo reflejado y la
amplitud A0 del rayo incidente:
A
R= 1
A0
Para un rayo que incide normalmente sobre una superficie, se puede deducir, en función de
las ecuaciones de Zoeppritz:
ρ ⋅ v − ρ 1 ⋅ v1 Z 2 − Z1
R= 2 2
=
ρ 2 ⋅ v 2 + ρ 1 ⋅ v1 Z 2 + Z1
donde ρ1, ν1 y Z1 y ρ2, ν2 y Z2 son los valores de la densidad, velocidad de las ondas P e
impedancia acústica del primer y segundo medio, respectivamente. Desde esta ecuación se deduce
que el valor de R oscila entre -1 y +1 (+1 ≥ R ≥ -1). Un valor negativo de R significa un cambio de
fase de π (180º) e el rayo reflejado.
El Coeficiente de Transmisión T es la razón entre la Amplitud A2 del rayo transmitido y la
Amplitud A0 del rayo incidente:
A
T= 2
A0
Para un rayo incidente normal dado, la solución de las ecuaciones de Zoeppritz
proporcionan:
2 ⋅ Z1
T=
Z 2 + Z1
Los coeficientes de Reflexión y Transmisión a veces se expresan en términos de energía, en
lugar de en términos de amplitud de las ondas. La Intensidad de energía (I) se define como la
cantidad de energía que fluye a través de una unidad de área normal a la dirección de propagación
de las ondas en la unidad de tiempo, dado que I0, I1 e I2 son las intensidades de los rayos incidente,
reflejado y transmitido, entonces:
I
 Z − Z1 
R' = 1 =  2

I 0  Z 2 + Z1 
2
y
T' =
I2
4 ⋅ Z1 ⋅ Z 2
=
I 0 ( Z 2 + Z1 ) 2
donde R’ y T’ son los coeficientes de reflexión y de Transmisión expresados en términos de energía.
Si R’ o R’ = 0, entonces toda la energía incidente es transmitida. Este caso se produce
cuando no hay contraste de Impedancia acústica a través de la superficie (Z1 = Z2), incluso si los
valores de densidad y de velocidad son diferentes en las dos capas. Si R o R’ = +1 o -1, toda la
energía incidente es reflejada. Una buena aproximación a esta situación se produce en la superficie
libre de una lámina de agua: los rayos que viajan hacia arriba desde una explosión en una capa de
agua, son totalmente reflejados en la superficie del agua, con un cambio de fase de π (R = -0.9995).
Los valores del coeficiente de Reflexión R para interfases entre diferentes tipos de rocas
raramente superan los ± 0.5, y son típicamente menores de ± 0.2. De este modo, la mayor parte de
la energía sísmica incidente en una interfase rocosa se transmite, y sólo una pequeña proporción es
reflejada.
A partir de una relación empírica entre la velocidad y la densidad (ver sección 6.9), resulta
posible calcular el coeficiente de reflexión únicamente a partir de información de velocidades
(Gardner et al., 1974; Meckel y Nath, 1977):
υ 
R = 0.625 ⋅ Ln  1 
 υ2 
6.2 Reflexión y Transmisión de los Rayos Sísmicos Incidentes Oblicuos
Cuando un rayo de ondas P incide oblicuamente sobre una interfase con contraste de
impedancia acústica, se generan rayos de ondas P reflejados y transmitidos, tal y como sucedía
cuando el rayo era normal. Además,
parte de la energía compresiva incidente
Sreflejado
se transforma en rayos S reflejados y
V1
transmitidos (Figura 3.6.1), que se
Preflejado
encuentran polarizados en un plano
vertical.
Pincidente
Las ecuaciones de Zoeppritz
muestran que las amplitudes de las cuatro
fases son función del ángulo de
V 2 > V1
incidencia (θ). Los rayos convertidos
pueden
alcanzar
una
magnitud
Prefractado
significativa para ángulos de incidencia
altos. Sin embargo, estos rayos sólo
Srefractado
tienen un interés menor en la prospección
sísmica y no se van a considerar.
θ
Figura 6.2: Rayos Reflejados y refractados generados por un
rayo P que incide oblicuamente sobre una interfase con
contraste de impedancia acústica.
En el caso de incidencia oblicua, los rayos-P transmitidos viajan a través de la capa inferior
con un cambio en la dirección de propagación (Figura 6.2), y son denominados rayos refractados.
Esta situación es análoga directamente al comportamiento de un rayo de luz incidente de un
modo oblicuo sobre el límite, por ejemplo entre el aire y el agua, y la Ley de Snell de la óptica se
aplica de un modo equivalente al caso de la sísmica. La forma generalizada de la Ley de Snell
establece que para cualquier rayo, la cantidad sen (i/v) permanece constante, y es conocida como el
parámetro de rayo (p), donde y es el ángulo de inclinación del rayo en una capa en la cual viaja
con una velocidad v.
Para el rayo-P refractado de la
figura 6.3 se verifica entonces:
sen θ 1 sen θ 2
=
v1
v2
o bien:
sen θ 1 v1
=
sen θ 2 v 2
Nótese que si V2 > V1 el rayo
refractado se aleja de la normal a la
superficie (θ2 > θ1). La ley de Snell también
se aplica al rayo reflejado, de donde se
deduce que el ángulo de reflexión es igual al
ángulo de incidencia (Figura 6.3).
Figura 6.3: Rayos P reflejados y refractados asociados a
un Rayo-P que incide de un modo oblicuo sobre una
interfase con contraste de Impedancia Acústica.
6.3 La Refracción Crítica
Cuando la velocidad de la capa inferior es mayor, existe un ángulo de incidencia conocido
como ángulo crítico (θ C), para el cual el ángulo de refracción es de 90º. Esto da lugar a un ángulo
refractado crítico que viaja a lo largo de la interfase a la velocidad mayor (V2). Para cualquier ángulo
mayor que el ángulo crítico existe una reflexión total interna de la energía incidente (además de los
Figura 6.4: Rayos Reflejados y refractados generados por un rayo P que incide oblicuamente sobre una
interfase con contraste de impedancia acústica.
rayos-S convertidos sobre un amplio rango de ángulos). Este ángulo crítico viene dado por:
sen θ C sen 90º 1
=
=
v1
v2
V2
por lo que:
v 
θ C = sen −1  1 
 v2 
El paso del rayo crítico refractado a lo largo del techo de la capa inferior causa una
perturbación en la capa superior que viaja hacia adelante a la velocidad V2, la cual es mayor que la
velocidad de la capa superior (V1). La situación es análoga a aquella de un proyectil viajando a
través del aire a una velocidad mayor que la del sonido, generando una onda de choque. En
prospección sísmica esta onda es conocida como onda de cabeza o de choque (head wave), y
pasa de un modo oblicuo a través de la capa superior hacia la superficie (Figura 6.4). Cualquier rayo
asociado con esta onda de choque presenta una inclinación igual al ángulo crítico (θC). Gracias a la
onda de choque, la energía sísmica regresa a la superficie después de una refracción crítica en una
capa situada por debajo y con una mayor velocidad.
6.4 - La Difracción
En la discusión anterior de la reflexión y transmisión de la energía sísmica en las interfaces de
contraste de impedancia acústica, estaba implícitamente asumida que las interfaces eran continuas y
con baja curvatura. En las discontinuidades abruptas en las interfases, o estructuras cuyos radios de
curvatura son más cortas que la longitud de onda de las ondas incidentes, las leyes de reflexión y
refracción no son aplicables. Tal fenómeno da lugar a una dispersión radial de la energía sísmica
incidente conocida como difracción (fig. 6.5). Ejemplos comunes de fuentes de difracción son las
cuñas de capas falladas, así como pequeños objetos aislados, tales como bloques en un medio
homogéneo.
Las fases difractadas se observan comúnmente en registros sísmicos y a veces son difíciles
de discriminar de las fases reflejadas y refractadas.
Frente de Onda
de la reflexión
Frente de Onda
Difracción
Falla
Figura 6.5: Difracción de la energía sísmica causada por el final truncado de una capa fallada.
SÍSMICA DE REFRACCIÓN - APUNTES DE PRÁCTICAS
Proporciona las velocidades en el medio (Vp y Vs), con lo que podemos conocer los
módulos de elasticidad, compacidad, grado de alteración, etc., por lo que es de gran aplicación en
Geotecnia.
En sísmica petrolera es un método complementario a la sísmica de reflexión, para poder
pasar las secciones de tiempo a secciones en profundidad. En sísmica de reflexión la representación
se realiza colocando sismogramas (tiempo), por lo que la representación es indirecta, mientras que
en sísmica de refracción se representan curvas tiempo-distancia denominadas dromocronas.
Se mide la primera perturbación que llega al geófono (bien la onda directa, o bien las ondas
refractadas). Esto es así porque a partir de un punto determinado se compensa el mayor espacio
recorrido con una mayor velocidad, y llega antes la onda refractada que la directa.
Los refractores vienen definidos por cambios de impedancia acústica (densidad ⋅
velocidad), y se produce una refracción total cuando el ángulo de incidencia alcanza un valor
determinado. A continuación vamos a ver las relaciones entre el tiempo y la distancia para diferentes
casos.
• Caso de la Onda Directa
Se representa un gráfico del Tiempo en función de la distancia, y la onda directa queda
reflejada por una recta que pasa por el origen y cuya pendiente es la inversa de la velocidad:
T=
X
V1
milisegs
metros
m = 1/ V2
distancia
crítica
m = 1/ V1
t1
geófonos
V1
Z
V
2
V <V
1
2
Figura 1: Trayectorias de los rayos directos, reflejados y refractados en una superficie cercana hacia un
detector, para el caso de un modelo geológico simple de dos capas.
• Caso de la Onda Refractada
En este caso se cumple que T = TAB +
TBC + TCD, y la ecuación que define el tiempo
en función de la distancia para el caso de dos
capas y V2 > V1 es:
T=
Z
X − 2 ⋅ Z ⋅ Tan ?
Z
+
+
V2
cos ? ⋅ V1
V1 ⋅ cos ?
Agrupando los términos en X, tenemos:
2
2
X 2 ⋅ Z V2 − V1
+
V2
V1 ⋅ V2
Esta ecuación es la de una recta cuya
pendiente es la inversa de la velocidad en el
segundo medio (m = 1 / V2), y el segundo
término independiente es la ordenada en el
origen de la dromocrona, que guarda relación
con las velocidades en el medio y la profundidad.
T=
• Caso de tres capas (dos medios)
Si tenemos dos medios, a partir de una distancia crítica recibo las refracciones de otra
litología, y las ecuaciones pasan a ser las siguientes:
T=
X 2 ⋅ Z 2 ⋅ cos θ C 2 ⋅ Z1 ⋅ cos θ1
+
+
V3
V2
V1
Que corresponde a la ecuación de una recta cuya pendiente es la inversa de la velocidad en
el tercer medio (1/V3) y el resto el término independiente (T2), que relaciona las velocidades y las
profundidades:
Z1 =
•
t1 ⋅V1 ⋅ V2
2 ⋅ V22 − V12
Z2 =
t 2 ⋅V2 ⋅V3
2 ⋅ V32 − V22
−
Z1 ⋅V2 ⋅ V32 − V12
V1 ⋅ V32 − V22
Caso general de n capas
X n. 1  2 ⋅ Z ⋅ cos θ i 
T = +∑

V3 i=1 
Vi

donde
sen θ i =
Vi
Vn
•
Caso de un refractor inclinado y plano
Este es el caso más general, y en él las ecuaciones son en función de unas velocidades
aparentes (denominadas D -down- y U -up-) debido al efecto de inclinación. Los refractores
inclinados se detectan mediante tiros de ida y vuelta, donde se observa que los trayectos para dos
capas no son simétricos. Las ecuaciones para los trayectos hacia abajo (D) y hacia arriba (U) son:
X ⋅ sen (θ + α ) 2 ⋅ Z D ⋅ cos θ
X ⋅ sen (θ − α ) 2 ⋅ ZU ⋅ cos θ
TDOWN =
+
y TUP =
+
V1
V1
V1
V1
2 ⋅ Z D ⋅ cos θ
X 2 ⋅ Z U ⋅ cos θ
y TUP =
+
VDOWN
V1
VUP
V1
V1
V1
VDOWN =
y VUP =
sen (θ + α )
sen (θ − α )
En este caso la inversa de la pendiente no es la velocidad de la capa inferior (V1), sino que ésta es
un valor intermedio entre las velocidades aparente U y D. Para hallar los valores de los ángulos (i,
α), tenemos:
TDOWN =
X
+
sen (θ − α ) = mU ⋅V1
y
sen (θ + α ) = m D ⋅V1
de donde:
1 
V
V 
1 
V
V 
α = ⋅  sen −1 1 − sen −1 1  y θ = ⋅  sen −1 1 + sen −1 1 
2 
VD
VU 
2 
VD
VU 
Como conozco V0, VU y VD a partir de la dromocrona, puedo obtener la V1 real (a partir de ZD y
TD):
DD ⋅ cos α = Z D
En cualquier caso, el tiempo final de retorno de los dos disparos de ida y de vuelta ha de ser el
mismo.