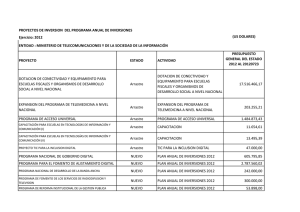
5.3 Dinámica del movimiento de arrastre. Dinámica de la pala.

Velocidades I
e aR
5. Dinámica de la pala
dFI
A
O
5.3 Dinámica del movimiento de arrastre
H
³
y
'
xr
dFc
P
dFa
El movimiento de la pala consiste en una rotación alrededor de la
articulación de arrastre caracterizada por el ángulo ζ .
151
AAD (HE)
Dinámica
Arrastre. Dinámica pala
1 / 10
Introducción
AAD (HE)
Dinámica
Arrastre. Dinámica pala
3 / 10
Velocidades II
El movimiento de las palas del rotor principal además del movimiento
de batimiento suele tener un movimiento en el plano de rotación
denominado movimiento de arrastre.
Cuando se desprecian las deformaciones de la pala, el movimiento de
arrastre se realiza a través de un movimiento de rotación como sólido
rígido, alrededor de una articulación denominada de arrastre.
El movimiento de arrastre debe de incluir siempre una separación en la
articulación de arrastre ya que en caso contrario no habría forma de
entregar el par al rotor.
Al igual que se hizo en el movimiento de batimiento, se añade un
modo ηa (x ) para caracterizar el movimiento en el plano, y , de forma
que y = ηa (x )ζ (t ).
Para el caso particular que se va a considerar de rotación de sólido
rígido, el modo ηa (x ) se expresa como:
⎧
⎨ (x − ea )
ηa (x ) =
1 − ea
⎩
0
x > ea
x < ea
donde la forma del modo se ha normalizado para que ηa (1) = 1.
La velocidad en el plano de referencia, UT , se expresa
adimensionalmente (considerandoζ ≪ 1):
UT
ζ̇
≈ x + µ sin ψ + ηa
ΩR
Ω
AAD (HE)
Dinámica
Arrastre. Dinámica pala
2 / 10
AAD (HE)
Dinámica
Arrastre. Dinámica pala
4 / 10
Equilibrio de momentos I
Equilibrio de momentos III
Resultando nalmente:
Las fuerzas que actúan sobre un elemento de pala:
dF
dF
fuerza aerodinámica: dFa ≈ dD + φ dL
2
2
¯
c fuerza centrífuga dFc = m Ω dr OP = m Ω dr y / sin ϕ . El momento
de la fuerza centrífuga con respecto a la articulación de arrastre será:
¯ ⋅ AH
¯ = m Ω2 dr y ea R .
dMc = mΩ2 dr OP
Es importante destacar que si la articulación de arrastre estuviera
situada en el eje de rotación el momento de la fuerza centrífuga sería
nulo.
dFI fuerza de inercia: dFI = m ÿRdr = m (ηa R )ζ̈ dr
ζ ′′ + νa2 ζ = γ M̄a
a
donde:
M̄a =
d F̄a =
∫ 1
eb
ηa d F̄a
dFa
ρ (ΩR )2 cR
y νa la frecuencia propia adimensional de arrastre:
∫R
ea R ea R (ηa R )m dr
2
νa =
∫
1 − ea eRR (ηa R )2 m dr
a
152
AAD (HE)
Dinámica
Arrastre. Dinámica pala
5 / 10
Equilibrio de momentos II
AAD (HE)
∫
1
ea ea ηa m dx
νa =
∫1
1 − ea e ηa2 m dx
a
2
Dinámica
Arrastre. Dinámica pala
7 / 10
Equilibrio de momentos IV
Caso particular de masa uniforme:
νa2 =
Equilibrio de momentos con respecto a la articulación de arrastre,
∑ MA = 0
∫ R
ea R
∫ R
∫ R
(ηa R )(r − ea R )m ζ̈ dr +
(ηa R )ea R m Ω2 ζ dr −
(r − ea R )dFa = 0
ea R
ea R
(∫ R
)
(∫ R
)
2
(ηa R )m dr Ω2 ea R ζ
(1 − ea )
(ηa R ) m dr ζ̈ +
ea R
ea R
∫ R
=
(r − ea R )dFa
ea R
3 ea
2 1 − ea
Dado que la componente en arrastre del momento producido por la
fuerza centrífuga es mucho menor que la componente en batimiento,
la frecuencia propia de arrastre es mucho menor y por tanto las
frecuencias propias de arrastre suelen presentar
valores:νa ≈ 0,2Ω − 0,3Ω
Algunos rotores articulados presentan un muelle en la articulación de
arrastre que proporciona rigidez o rotores rígidos de forma que
consiguen una frecuencia propia mayor. Los rotores rígidos pueden
clasicarse como
de arrastre blando: νa ≈ 0,6Ω − 0,8Ω
de arrastre rígido: νa ≈ 1,4Ω − 1,6Ω
AAD (HE)
Dinámica
Arrastre. Dinámica pala
6 / 10
AAD (HE)
Dinámica
Arrastre. Dinámica pala
8 / 10
Equilibrio de momentos V
Caso particular de separación de articulación de arrastre nula, ea = 0
implica νa = 0
El movimiento de arrastre es menos amortiguado que el movimiento
de batimiento. Esto es debido a que:
el amortiguamiento en arrastre aparece por el cambio que sufren las
fuerzas aerodinámicas debidas al cambio de la velocidad tangencial al
perl. Sin embargo, en batimiento la modicación de las fuerzas es
debida a un cambio en la velocidad perpendicular, siendo el efecto
mucho más directo (el efecto en el ángulo de ataque es mayor).
las fuerzas aerodinámicas que intervienen en la dinámica de arrastre
provienen de fuerzas de resistencia aerodinámicas por lo que son
fuerzas un orden de magnitud inferior a las que intervienen en la
dinámica de batimiento (sustentación).
153
AAD (HE)
Dinámica
Arrastre. Dinámica pala
9 / 10
Equilibrio de momentos VI
Consecuencia: el movimiento de arrastre es propenso por su bajo
amortiguamiento a problemas aeroelásticos.
Ejemplo: resonancia de tierra (ground resonance). Este efecto consiste
en el acoplamiento entre la dinámica del movimiento de arrastre con la
dinámica lateral del fuselaje. Suele aparecer en rotores articulados con
poco amortiguamiento en arrastre o en rotores rígidos con arrastre
blando, es decir con frecuencias propias menores que la frecuencia de
excitación.
Habitualmente se introducen amortiguadores para proporcionar
amortiguamiento al movimiento de arrastre que conducen a la
eliminación de estos problemas aeroelásticos.
AAD (HE)
Dinámica
Arrastre. Dinámica pala
10 / 10