tasa de cambio promedio

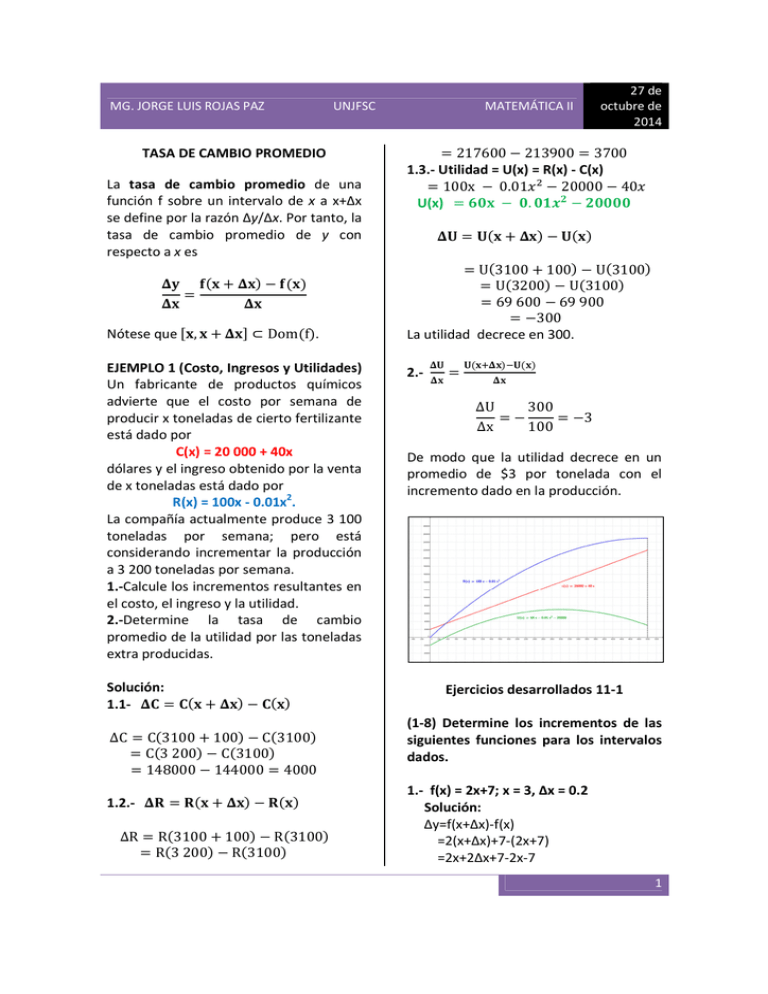
MG. JORGE LUIS ROJAS PAZ
UNJFSC
TASA DE CAMBIO PROMEDIO
La tasa de cambio promedio de una
función f sobre un intervalo de x a x+Δx
se define por la razón Δy/Δx. Por tanto, la
tasa de cambio promedio de y con
respecto a x es
Nótese que
,
⊂ Dom f .
EJEMPLO 1 (Costo, Ingresos y Utilidades)
Un fabricante de productos químicos
advierte que el costo por semana de
producir x toneladas de cierto fertilizante
está dado por
C(x) = 20 000 + 40x
dólares y el ingreso obtenido por la venta
de x toneladas está dado por
R(x) = 100x - 0.01x2.
La compañía actualmente produce 3 100
toneladas por semana; pero está
considerando incrementar la producción
a 3 200 toneladas por semana.
1.-Calcule los incrementos resultantes en
el costo, el ingreso y la utilidad.
2.-Determine la tasa de cambio
promedio de la utilidad por las toneladas
extra producidas.
Solución:
1.1- ΔC
C 3100
C 3200
148000
R 3100
R 3200
217600 213900 3700
1.3.- Utilidad = U(x) = R(x) - C(x)
100x 0.01# $ 20000 40#
U(x) %& &. &'() )&&&&
*
*
*
U 3100 100
U 3100
U 3200
U 3100
69600 69900
300
La utilidad decrece en 300.
2.-
*
* ,
ΔU
Δx
-*
300
100
3
De modo que la utilidad decrece en un
promedio de $3 por tonelada con el
incremento dado en la producción.
Ejercicios desarrollados 11-1
100
C 3100
C 3100
144000 4000
1.2.- ΔR
27 de
octubre de
2014
MATEMÁTICA II
100
R 3100
R 3100
(1-8) Determine los incrementos de las
siguientes funciones para los intervalos
dados.
1.- f(x) = 2x+7; x = 3, Δx = 0.2
Solución:
Δy=f(x+Δx)-f(x)
=2(x+Δx)+7-(2x+7)
=2x+2Δx+7-2x-7
1
MG. JORGE LUIS ROJAS PAZ
UNJFSC
=2Δx
Δy=2(0.2)=0.4
2.)() . /; ),
= &. /
Solución:
Δy=f(x+Δx)-f(x)
=2(x+Δx)2+3(x+Δx) – 5 – (2x2 + 3x – 5)
=2x2+4xΔx+2(Δx)2+3x+3Δx–5–2x2-3x+5
=2(Δx)2+4xΔx+3Δx
Δy=2(0.5)2+4(2)(0.5)+3(0.5)=6
() -2
3.- 1
= -) ; ( = ',
Solución:
Δy = g(x+Δx)-g(x)
Δy =
Δy =
4,54 6 -7
4,54 -$
9,$
6 -7
9,$ -$
−
−
=)
− 2000
500
− 2000
1 + t + Δt $
500
+
1 + t$
500
500
Δp =
−
$
1 + t + Δt
1 + t$
Δp = 2000 +
6.- C
= D() + E( + F; (G( + H(
Solución:
9-$
Δy = 5 − 3 = 2
Δh = h(x+Δx)-h(x)
==/
Δh = a # + ?# $ + K # + ?# + L
− a# $ + K# + L
Δf = f(t+Δt)-f(t)
Δf =
900
900
−
t + ?@
t
Δf =
900
900
−
25 + 5 25
Δh = a # $ + 2#?# + ?# $ + K#
+ K?# + L − a# $ − K#
−L
Δh = a# $ + 2M#?# + M ?# $ + K#
+ K?# + L − a# $ − K#
−L
Δh = 2M#?# + M ?#
Δf = 30 − 36 = −6
5.- A ; = )&&& + ) ; ; = ),
',=
Solución:
Δp = p(t+Δt)-p(t)
$
Δp = −50
96 -7
/&&
500
1 + t + Δt
500
+
1 + t$
500
500
−
$
1+ 2+1
1 + 2$
500 500
−
= −50
Δp =
10
5
4-$
; ; = )/,
4.- ; =
=
Solución:
Δp = 2000 +
Δp =
8 6 -7
<&&
27 de
octubre de
2014
MATEMÁTICA II
=='
$
+ K?#
)
7.- N
= + ; (G( +
(
Solución:
ΔF = F(x+Δx)-F(x)
2
MG. JORGE LUIS ROJAS PAZ
Δf =
+
+
UNJFSC
)
−
( + H(
$
+
)
(
$
Δf = Δx + 4,54 − 4
MATEMÁTICA II
10.- ( = .() − / + '; ( = .,
=
&. )
Solución
La tasa de cambio promedio la
calculamos, usando la formula siguiente:
/
8.- O = = .&& + ;,' ; ;G; + =
Solución:
ΔG = G(t+Δt)-G(t)
/
− .&&
; + H; + '
/
+
;+'
/
ΔG = .&& +
− .&&
; + H; + '
/
−
;+'
/
/
ΔG =
−
;,H; ,'
;,'
(9-16) Calcule la tasa de cambio
promedio de cada función en el
intervalo dado.
9.- ( = . − Q ; ( = ),
= &. /
Solución
La tasa de cambio promedio la
calculamos, usando la formula siguiente:
=
=
.−Q
=
-Q
=
=
ΔG = .&& +
+
−
+
− .−Q
= −Q
27 de
octubre de
2014
=
. ,
) -/
,
+
−
,'-.() ,/ -'
.() ,%(H(,. H( ) -/(-/H(,'-.() ,/ -'
6#?# + 3 ?#
=
Δx
$
− 5?#
= 6x + 3Δx − 5
Δy
= 6 3 + 3 0.2 − 5
Δx
5R
54
= 13.6
() -<
11.- 1 ( =
; ( = ),
= &. /
(-.
Solución
La tasa de cambio promedio la
calculamos, usando la formula siguiente:
Δy g x + Δx − g x
=
Δx
Δx
Reemplazando tenemos:
)
+
− < () − <
−
(−.
+
−.
=
=
(,H( ,.- -.
='
3
MG. JORGE LUIS ROJAS PAZ
UNJFSC
.() ,'
12.- h (
; ( /,
= &. .
(
Solución
La tasa de cambio promedio la
calculamos, usando la formula siguiente:
MATEMÁTICA II
.
14.-F ( = ; (G( +
W
Solución
La tasa de cambio promedio la
calculamos, usando la formula siguiente:
Δy F x + Δx − F x
=
Δx
Δx
Reemplazando tenemos:
Δy h x + Δx − h x
=
Δx
Δx
Reemplazando tenemos:
Δy
=
Δx
Δy
=
Δx
)
27 de
octubre de
2014
3
3
Δy # + ?# − # =
Δx
Δx
)
. ( + H( + ' .( + '
−
( + H(
(
Δx
Δy
=
Δx
. / + &. . ) + ' . / ) + '
−
/ + &. .
/
0.3
3# − 3# − 3?#
# # + ?#
Δx
Δy
−3?#
=
Δx #?# # + ?#
Δy
−3
=
Δx # # + ?#
5R
= 2.962264150
54
13. - f ; = √2 + ;; ; = /, = = '. )2
Solución
La tasa de cambio promedio la
calculamos, usando la formula siguiente:
15.-G ; = = . + =; ; = "G"G"G + Z"
Solución
La tasa de cambio promedio la
calculamos, usando la formula siguiente:
Δy f t + Δt − f t
=
Δt
Δt
Δy G a + h − G a
=
Δt
h
Δy U4 + @ + ?@ − √4 + @
=
Δt
Δt
Δy U4 + 5 + 1.24 − √4 + 5
=
Δt
1.24
5R
5V
= 0.1612903225
Reemplazando tenemos
Δy
a+h
=
Δt
5R
=
5R
=
5V
5V
[
+ a + h − M[ − a
h
\] ,[\6 ^,[\^6 ,^] , \,^ -_] -\
^
[\6 ^,[\^6 ,^] ,^
5R
5V
^
= 3a$ + 3Mℎ + ℎ$ + 1
4
MG. JORGE LUIS ROJAS PAZ
UNJFSC
.
16.-f (
; "("G"( H("
)(,'
Solución
La tasa de cambio promedio la
calculamos, usando la formula siguiente:
Δy f x + Δx − f x
=
Δx
Δx
Reemplazando:
3
3
Δy 2 # + ?# + 1 − 2# + 1
=
Δx
Δx
Simplificando
Δy 3 2# + 1 − 3 2 # + ?# + 1
=
Δx 2 # + ?# + 1 2# + 1
Δx
Δy
6# + 3 − 6 # + ?# − 3
=
Δx Δx 2 # + ?# + 1 2# + 1
Δy
6# + 3 − 6# − 6?# − 3
=
Δx Δx 2 # + ?# + 1 2# + 1
Δy
−6
=
Δx
2 x + Δx + 1 2x + 1
Solución
La tasa de cambio
calculamos, usando:
p (t)=10 000 +1 000 t -120@ $
Determine la tasa de crecimiento
promedio entre cada par de tiempos.
a)
b)
c)
d)
e)
t= 3 y t=5 años.
t=3 y t=4 años.
t=3 y t = 39$ años.
t=3 y t = 397 años.
t y t+Δt años.
promedio
la
Δy p t + Δt − p t
=
Δt
Δt
y reemplazando:
a) t= 3 y t=5 años.
Δy p 3 + 2 − p 3
=
Δt
2
c 5 = 12000
c 3 = 11920
5R
5V
=
9$ddd-99e$d
$
=40
b) t=3 y t=4 años.
Δy p 3 + 1 − p 3
=
1
Δt
c 4 = 12080
c 3 = 11920
5R
17.- (Crecimiento y variación de la
población) El tamaño de la población de
cierto centro minero al tiempo t (medido
en años) está dado por
27 de
octubre de
2014
MATEMÁTICA II
5V
=
9$dfd-99e$d
9
= 160
c) t=3 y t = 39$ años.
1
Δy p g3 + 2h − p 3
=
1
Δt
2
i
c g$h = 12030
c 3 = 11920
5R
5V
=
9$d[d-99e$d
j
6
= 220
5
MG. JORGE LUIS ROJAS PAZ
d) t=3 y t
UNJFSC
397 años.
1
Δy p g3 + 4h − p 3
=
1
Δt
4
MATEMÁTICA II
3.- 1
=
Solución:
() -2
-)
; ( = ',
27 de
octubre de
2014
=)
9[
c g h = 11982.5
7
c 3 = 11920
5R
5V
=
99ef$.k-99e$d
j
l
= 250
e) t y t+Δt años.
Δy p t + Δt − p t
=
=
Δt
Δt
9dddd,9ddd V,5V -9$d V,5V 6 -9dddd-9dddV,9$dm 6
5V
=
=
9ddd V,5V -9$d V,5V 6 -9dddV,9$dm 6
5V
9dddV,9ddd5V-9$dm 6 -$7dV5V-9$d nm 6 -9dddV,9$dm 6
=
5V
9ddd5V-$7dV5V-9$d nm 6
5V
5R
5V
= 1000 − 240@ − 120?@
6