GUÍA DE ONDA RECTANGULAR ∫∫ ∫ ∫

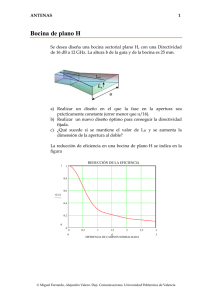
ANTENAS
1
GUÍA DE ONDA RECTANGULAR
Una guía de onda en la que se propaga el modo TE10, abierta en su
extremo , tiene una distribución de campos en la apertura con
polarización vertical.
G
E = E y yˆ
G
E
H = H x xˆ = − y xˆ
Z0
La forma de la distribución es coseno en el eje x y uniforme en el eje
⎛π
E y = E0 cos ⎜
⎝a
Ey
Hx = −
Z0
Z0 =
⎞
x⎟
⎠
η
⎛ λ ⎞
1− ⎜ ⎟
⎝ 2a ⎠
2
La impedancia de la guía de onda se aproxima a la del espacio libre
si aumenta la frecuencia.
Los campos radiados por una apertura rectangular, con polarización
vertical son
⎛η
⎞
e − jkr
jk y '
Eθ = j
sin φ ⎜ cos θ + 1⎟ ∫∫ E ( x ', y ' ) e jkx x 'e y dx ' dy '
2λ r
⎝ Z0
⎠ s'
− jkr
⎛η
⎞
e
jk y '
Eφ = j
cos φ ⎜ + cos θ ⎟ ∫∫ E ( x ', y ') e jkx x 'e y dx ' dy '
2λ r
⎝ Z0
⎠ s'
Los campos de la apertura son separables en el producto de dos
funciones
∫∫ E ( x ', y ') e
s'
jk x x '
e
jk y y '
dx ' dy ' = E0 ∫ f ( x ' ) e jkx x ' dx ' ∫ g ( y ')e
x'
jk y y '
dy '
y'
Las dos integrales unidimensionales son transformadas de Fourier
de la distribución de campos
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
2
La distribución horizontal corresponde a una función coseno,
mientras que la distribución vertical es una función uniforme.
⎛k a⎞
cos ⎜ x ⎟
π
⎝ 2 ⎠
F (k x , a ) = ∫ f ( x ' ) e jkx x ' dx ' = a
2
2 ⎛ π ⎞ ⎛ k x a ⎞2
a
−
⎜ ⎟ −⎜
⎟
2
⎝2⎠ ⎝ 2 ⎠
⎛k b⎞
b
sin ⎜ y ⎟
2
jk y '
⎝ 2 ⎠
G (k y , b) = ∫ g ( y ' ) e y dy ' = b
⎛ k yb ⎞
b
−
⎜
⎟
2
⎝ 2 ⎠
a
2
Una bocina en el modo fundamental tiene un diagrama de radiación
poco directivo.
Los diagramas plano E y plano H para una guía de banda X de
22.8x10.2 mm , a la frecuencia de 10 GHz son
1
0.8
f H( θ )
f E( θ )
0.6
0.4
0.278 0.2
1
−π
0
1
θ
π
2
2
El diagrama tridimensional es
z
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
3
BOCINAS RECTANGULARES
Una bocina electromagnética es una antena que se utiliza de forma
generalizada a frecuencias de microondas, por sus características de
gran ancho de banda y por su facilidad de construcción y diseño.
Se utiliza como antena individual, en forma de agrupaciones, o como
alimentador primario de reflectores o lentes.
Una bocina se alimenta a partir de una guía de onda que propaga
uno o varios modos.
Las dimensiones van aumentando
progresivamente hasta que la apertura equivalente tenga unas
dimensiones suficientes para conseguir la directividad desesada.
Las guías de onda rectangulares que propagan el modo fundamental
TE10, se pueden abrir en el plano horizontal, dando lugar a las
denominadas bocinas de plano H; en el plano vertical, formando las
bocinas de plano E; o bien en ambos planos simultáneamente dando
lugar a bocinas piramidales.
Bocina de plano H
Bocina de plano E
Bocina piramidal
Las guías de onda circulares, que propagan el modo fundamental
TE11, alimentan a las bocinas cónicas
Bocina cónica
Estas antenas se pueden analizar como aperturas, suponiendo que la
distribución de los campos es aproximadamente la misma que los
modos de las guías rectangulares o circulares.
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
4
Campos en la apertura
La distribución de campos boca de guía rectangular en el modo
fundamental TE10 es
⎛π x ⎞
E y = E0 cos ⎜
⎟
⎝ a ⎠
En las bocinas de plano E se aumentan las dimensiones verticales de
la apertura.
b
bg
a
Para aumentar la directividad, se puede aumentar las dimensiones
verticales de la apertura, apareciendo una diferencia de fase en la
bocina de plano E.
R
y
LE
β ( R − LE ) = β
(
β ( R − LE ) = β
y2
y2
=β
2 LE
2 LE
2
y + LE − LE
2
)
⎛ ⎛ 1 ⎛ y ⎞2 ⎞
⎞
β ⎜ LE ⎜1 + ⎜ ⎟ ⎟ − LE ⎟
⎜ ⎜ 2⎝ R⎠ ⎟
⎟
⎠
⎝ ⎝
⎠
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
5
La diferencia de fase tiene un comportamiento proporcional al
cuadrado de la distancia. La distribución de campos en las bocinas
de plano E será el mismo que la boca de guía rectangular con un
término de fase adicional
β y2
⎛ π x ⎞ − j 2 LE
E y = E0 cos ⎜
⎟e
⎝ a ⎠
Si se aumentan las dimensiones en el plano horizontal, la bocina se
denomina de plano H, en este caso el error de fase cuadrático
depende de la posición x. La distribución de amplitudes es la misma
del modo fundamental de la guía de ondas.
LH
Ey
a
β x2
⎛ π x ⎞ − j 2 LH
E y = E0 cos ⎜
⎟e
⎝ a ⎠
En una bocina de forma piramidal aumentan las dimensiones
horizontales y verticales de la bocina, el error de fase aparece en
ambos planos.
β x2
β y2
⎛ π x ⎞ − j 2 LH − j 2 LE
E y = E0 cos ⎜
e
⎟e
⎝ a ⎠
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
6
En la siguiente tabla se comparan las distribuciones de campos en las
bocinas.
β y2
Bocina de plano E
⎛ π x ⎞ − j 2 LE
E y = E0 cos ⎜
⎟e
⎝ a ⎠
Bocina de plano H
⎛ π x ⎞ − j 2 LH
E y = E0 cos ⎜
⎟e
⎝ a ⎠
Bocina piramidal
⎛ π x ⎞ − j 2 LH − j 2 LE
E y = E0 cos ⎜
e
⎟e
⎝ a ⎠
β x2
β x2
β y2
El máximo error de fase en el extremo de la bocina con respecto al
centro
2
⎛a⎞
⎜ ⎟
a2
2⎠
⎝
=β
β ( Rm − LH ) = β
2 LH
8LH
2
⎛b⎞
⎜ ⎟
b2
2
β ( Rm − LE ) = β ⎝ ⎠ = β
2 LE
8 LE
En las bocinas se puede aproximar la constante de propagación por
la del espacio libre
k ( Rm − LH ) =
2π a 2
= 2π t
λ 8LH
k ( Rm − LE ) =
2π b 2
= 2π s
λ 8 LE
Los parámetros s,t son las diferencias en longitudes de onda entre el
centro de la bocina y los extremos de los cortes x,y.
t=
a2
8λ LH
s=
b2
8λ LE
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
7
Gráficas de los campos en la apertura
Campos Ey en una bocina piramidal. Modo TE10
Módulo
Fase
Real(Ey)
Im(Ey)
Campos en la apertura t=3/8 s=1/4
Distribución horizontal y vertical (módulo y fase)
0
1
1
0.75
0.75
0.5
0.5
0.25
0.25
0
1
0.5
0
0.5
1
0
0
1
0.5
|Ey(x)|
3.14
1.57
1.57
0
0
1.57
1.57
1
0.5
0
arg(Ey(x))
0.5
1
|Ey(y)|
3.14
3.14
0
0.5
1
3.14
1
0.5
0
0.5
arg(Ey(y))
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
1
ANTENAS
8
Campos radiados por las bocinas
Los campos radiados en una apertura rectangular son proporcionales
a las transformadas de Fourier de las distribución de campos en la
apertura.
∫∫ E ( x ', y ') e
jk x x '
e
jk y y '
s'
dx ' dy ' = E0 ∫ f ( x ' ) e jkx x ' dx ' ∫ g ( y ')e
x'
jk y y '
dy '
y'
Para calcular los campos se pueden calcular las siguientes integrales
normalizadas (cambio de variable x’=ax/2)
⎛π
F ( k x , t ) = ∫ cos ⎜
⎝2
−1
1
1
G ( k y , s ) = ∫ e − j 2π sy e
2
a
jk x x
2
⎞
x ⎟e − j 2π tx e 2 dx
⎠
b
jk y y
2
dy
−1
Las funciones a integrar son las funciones coseno y uniforme, con
2
errores cuadráticos de fase proporcionales a −2π sx . En los extremos
se tendrá el error máximo de fase. El parámetro t es la diferencia en
longitudes de onda de LH y R. El parámetro s es la diferencia en
longitudes de onda de LE y R.
Si los errores de fase
son pequeños los diagramas serán
proporcionales a las transformadas de las funciones uniforme y
coseno. Si el error cuadrático aumenta los diagramas se modifican ,
con un efecto de relleno de los nulos.
En las siguientes gráficas universales se representan las
transformadas de Fourier de las funciones con error cuadrático para
diversas diferencias de camino entre el centro y el extremo.
Los primeros ceros de los diagramas aparecen en u=π en la
distribución uniforme y u=1.5π.
u=
ka sin θ
2
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
9
Diagramas de radiación de las bocinas
Distribución coseno con errores de fase
1
0.8
0.6
0.4
t=1
0.2
0.75
0.5
0.25
t=0
0
0
2
4
0
6
8
u
10
10
Distribución uniforme con errores de fase
1
0.8
0.6
s=1
0.4
0.75
0.50
0.2
0.25
s=0
0
0
0
2
4
6
u
8
10
10
Los diagramas de radiación de las bocinas en formato de curvas de
nivel son
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
10
Transformada de los campos en la bocina con errores de fase
s=1/8,t=1/8
Transformada de los campos en la bocina con errores de fase
t=3/8,s=1/4
Las bocinas sectoriales tienen diagramas en forma de
abanico,mientras que las piramidales tienen diagramas tipo pincel.
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
11
Directividad de las bocinas
En una apertura rectangular, la directividad se puede calcular como
D=
4π
λ
2
Aef =
4π
λ
2
abηil =
4π
λ2
abηilxηily
Las eficiencias de iluminación son
ηilx =
∫
∫
1/ 2
−1/ 2
1/ 2
−1/ 2
f ( x ) dx
2
f ( x ) dx
2
ηily =
∫
∫
1/ 2
−1/ 2
1/ 2
−1/ 2
g ( y ) dy
2
g ( y ) dy
2
En caso de no tener error de fase las eficiencias se calculan de forma
simple
8
⎛π ⎞
f1 ( x ) = cos ⎜ x ⎟ ηilx = 2
π
⎝2 ⎠
La distribución uniforme tiene eficiencia 1
g1 ( y ) = 1 ηily = 1
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
12
Si la distribución tiene error de fase
2
⎛π ⎞
f 2 ( x ) = cos ⎜ x ⎟ e− j 2π t x
⎝2 ⎠
La eficiencia se multiplica por un factor que tiene en cuenta el error
de fase. El cálculo se puede realizar de forma simple mediante
integración numérica.
1
REDUCCIÓN DE LA EFICIENCIA
1
0.8
0.6
f ( s1)
0.4
0.2
0
0
0
0.5
0
1
1.5
2
2.5
s1
DIFERENCIA DE CAMINOS NORMALIZADA
3
3
Las distribuciones uniformes con error de fase son
g 2 ( y ) = e − j 2π s y
1
2
REDUCCIÓN DE LA EFICIENCIA
1
0.8
0.6
g( t1)
0.4
0.2
0
0
0
0
0.5
1
1.5
2
t1
DIFERENCIA DE CAMINOS NORMALIZADA
2.5
3
3
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
13
Para aperturas rectangulares de dimensiones a, b las directividades
serán
4π
8
η (s)
λ
π 2 y2
4π
DH = 2 abgη x 2 ( t )
λ
4π
D pir = 2 abη x 2 ( t )η y 2 ( s )
λ
DE =
2
ag b
Siendo ag y bg las dimensiones de la guía de alimentación. Se puede
calcular la directividad de la bocina piramidal en función de las
directividades correspondientes a las bocinas plano E y H, que
presentan su mismo error de fase en la distribución del plano
abocinado.
D pir =
⎛ λ 2 DE ⎞ ⎛ λ 2 DH
ab
⎜
⎟⎜
λ 2 ⎜⎝ 4π ag b ⎟⎠ ⎜⎝ 4π abg
4π
⎞
⎟⎟
⎠
⎛λ
⎞⎛ λ
⎞π
D pir = ⎜ DE ⎟ ⎜ DH ⎟
⎜a
⎟⎜ b
⎟ 32
⎝ g
⎠⎝ g
⎠
Bocinas óptimas
La directividad de las bocinas depende del área de la apertura y del
producto de las eficiencias.
Por otra parte las dimensiones están relacionadas con los errores de
fase mediante las relaciones
t=
a2
8λ LH
s=
b2
8λ LE
a = t 8λ LH
b = s8λ LE
Si la longitud de la bocina se mantiene constante, la Directividad
crecerá proporcionalmente a la raíz cuadrada del parámetro t, s.
La representación gráfica de la función eficiencia por dicha raíz
cuadrada permite observar que existe un punto óptimo, que es
t=3/8, s=1/4 que coincide con diferencias de fase de 135º en el plano
H y 90º en el plano E, equivalentes a diferencias de camino de 3λ/8
en el plano H,y λ/4 en el E. La diferencia de óptimos es debida a la
mayor atenuación del módulo del campo en la distribución coseno.
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
14
BOCINAS PLANO H ÓPTIMAS
1
1
0.8
f ( s1)
0.6
s1
f ( s1) ⋅ s1
0.4
0.2
0
0
0
0.5
0
1
1
1.5
2
2.5
3
s1
DIFERENCIA DE CAMINOS NORMALIZADA
3
BOCINAS PLANO E ÓPTIMAS
1
0.8
g( t)
0.6
t
g( t) ⋅ t
0.4
0.2
0
0
0
0
Bocina plano E
Bocina plano H
0.5
1
1.5
2
t
DIFERENCIA DE CAMINOS NORMALIZADA
Diferencia
caminos
b2
λ
=
8 LE 4
a2
3λ
=
8LH
8
Diferencia fase
β
b2 π
=
8 LE 2
β
a2
3π
=
8 LH
4
2.5
3
3
Dimensiones
b = 2λ LE
a = 3λ LH
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
15
La Directividad de las aperturas se puede representar en unas
gráficas normalizadas, que dependen básicamente de las funciones
g(s) y f(t) de reducción de la eficiencia.
λ
⎛ b ⎞ 32
DE = ⎜ ⎟ g ( s )
ag
⎝λ⎠ π
b2
s=
8λ LE
λ
⎛ a ⎞ 32
DH = ⎜ ⎟
f (t )
bg
⎝λ⎠ π
0 120
t=
a2
8λ LH
DIRECTIVIDAD DE LAS BOCINAS DE PLANO E
L=100λ
100
80
DEλ/ag
L=50λ
60
L=20λ
40
20
L=10λ
0
0
140
5
10
b/λ
15
20
DIRECTIVIDAD DE LAS BOCINAS DE PLANO H
L=100λ
120
100
DHλ/bg
L=50λ
80
60
L=20λ
40
L=10λ
20
0
5
10
a/λ
15
20
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
16
GUÍA DE ONDAS CIRCULAR
Una guía de ondas circular propaga el modo fundamental TE11. Las
expresiones del campo para el modo son
Eρ = Eo
ρ⎞
⎛
J1 ⎜1.841 ⎟ sin φ
a⎠
ρ ⎝
Eφ = Eo
1 ∂ ⎛ ⎛
ρ ⎞⎞
J1 ⎜1.841 ⎟ ⎟ cos φ
⎜
ρ ∂ρ ⎝ ⎝
a ⎠⎠
1
Ez = 0
La representación gráfica de los campos es
Eρ
Eφ
Las líneas de campo se pueden visualizar a partir de la
representación gráfica de Hz.
Se puede observar que las líneas de
campo son perpendiculares al
contorno, y por lo tanto el campo
tangencial es cero.
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
17
Para el cálculo de la radiación es más conveniente utilizar las
componentes Ex, Ey del campo.
Dichas componentes en coordenadas cartesianas están relacionadas
con las componentes en cilíndricas mediante
E y = Eρ sin φ + Eφ cos φ
Ex = Eρ cos φ − Eφ sin φ
En las aperturas circulares se ha demostrado que
Ey = Ey 45 − E x 45 cos 2φ
E x = E x 45 sin 2φ
El corte a 45º del campo en la apertura es
1.841
ρ
J 0 1.841
2a
a
1.841
ρ
E x 45 ( ρ ) =
J 2 1.841
2a
a
Ey 45 ( ρ ) =
(
(
)
)
La representación gráfica de las componentes copolares y de
polarización cruzada en la apertura es
El diagrama de radiación se puede calcular a partir de las
transformadas de las componentes copolares y de polarización
cruzada en la diagonal.
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
18
BOCINAS CÓNICAS
ρ
L
a
La distribución de campos en una bocina cónica tiene la misma
forma que el modo fundamental en la guía, y al igual que en las
bocinas piramidales aparece un error cuadrático de fase debido a la
diferencia de caminos recorridos por las ondas.
Eρ = Eo e
Eφ = Eo e
⎛ρ⎞
− j 2π s ⎜ ⎟
⎝a⎠
⎛ρ⎞
− j 2π s ⎜ ⎟
⎝a⎠
d m2
,
s=
8λ L
2
2
ρ⎞
⎛
J1 ⎜ 1.841 ⎟ sin φ
a⎠
ρ ⎝
1
1 ∂ ⎛ ⎛
ρ ⎞⎞
J1 ⎜1.841 ⎟ ⎟ cos φ
⎜
ρ ∂ρ ⎝ ⎝
a ⎠⎠
d m = 2a
Para el cálculo del diagrama es necesario determinar el campo en la
diagonal
ρ 2
1.841
ρ
J 0 1.841 e − j 2 πs( a )
2a
a
ρ 2
ρ
1.841
E x 45 ( ρ ) =
J 2 1.841 e − j 2 πs( a )
2a
a
(
(
Ey 45 ( ρ ) =
)
)
Las funciones transformadas son
a
Fo ( u ) = 2π ∫ E y 45 ( ρ ) J o ( k ρ sin θ )ρ d ρ
0
a
F2 ( u ) = 2π ∫ Ex 45 ( ρ ) J 2 ( k ρ sin θ )ρ d ρ
0
u = ka sin θ
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
19
En las siguientes gráficas se muestran los diagramas normalizados en
función del error máximo de fase para las componentes copolar y
contrapolar o cruzada, en función del máximo error de fase.
0
0
f ( u , 0)
f ⎛⎜ u ,
⎝
⎛
⎝
f⎜ u ,
1⎞
8⎠
10
0.5
1⎞
0.25
4 ⎠ 20
0.125
3
f ⎛⎜ u , ⎞
⎝ 8⎠
⎛
⎝
f⎜ u ,
1⎞
2⎠
0.375
s=0
30
− 40 40
10
5
− 10
0
5
10
u
10
Diagramas de la polarización de referencia a 45º
− 18.297
g( u , 0)
g⎛⎜ u ,
1⎞
8⎠
⎛
⎝
1⎞
⎝
g⎜ u ,
g⎛⎜ u ,
⎝
⎛
⎝
g⎜ u ,
15
20
s=1/2
25
4⎠
3 ⎞ 30
8⎠
1⎞
2 ⎠ 35
− 40 40
s=0
10
− 10
5
0
u
5
10
10
Diagramas de la polarización cruzada a 45º
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
20
Los diagramas copolares y de polarización cruzada, para un error
s=1/8 se muestran en las siguientes figuras, en función del
parámetro u
Directividad de las bocinas cónicas
La Directividad de una apertura circular es
D=
4π
λ
2
Aef =
4π
λ
2
(π a ) η
2
il
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia
ANTENAS
21
La eficiencia para una guía de onda circular sobredimensionada, a>λ
con el modo TE11, tiene una eficiencia de 0.837.
La Directividad se reduce según el error de fase en la bocina
En la gráfica se muestra dicho error de fase en función del parámetro
s.
1
1
0.8
0.6
2
0.4
0.2
0
0
0
0.5
0
1
1.5
2
2.5
s1
3
3
En la figura se muestran las gráficas para la directividad de una
bocina cónica en función de sus dimensiones.
El óptimo se tiene cuando la diferencia de caminos entre los puntos
extremos de la boca es s=3/8, igual que en la bocina de plano H
30.293
35
L=20λ
L=10λ
28
D (dB)
L=5λ
D( a , 20) 21
L=2λ
D( a , 10)
D( a , 5)
D( a , 2)
0
14
7
3.393
0
1
1
a/λ
10
a
10
© Miguel Ferrando, Alejandro Valero. Dep. Comunicaciones. Universidad Politécnica de Valencia