FIABILIDAD (I): CONCEPTOS BÁSICOS

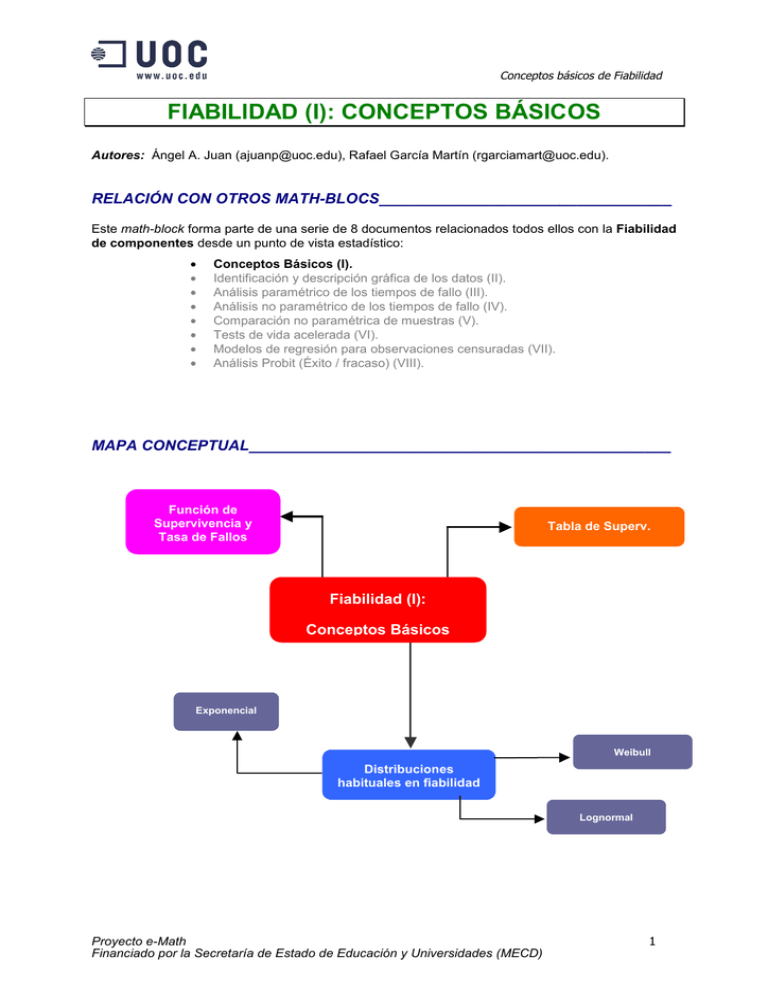
Conceptos básicos de Fiabilidad
FIABILIDAD (I): CONCEPTOS BÁSICOS
Autores: Ángel A. Juan ([email protected]), Rafael García Martín ([email protected]).
RELACIÓN CON OTROS MATH-BLOCS__________________________________
Este math-block forma parte de una serie de 8 documentos relacionados todos ellos con la Fiabilidad
de componentes desde un punto de vista estadístico:
•
•
•
•
•
•
•
•
Conceptos Básicos (I).
Identificación y descripción gráfica de los datos (II).
Análisis paramétrico de los tiempos de fallo (III).
Análisis no paramétrico de los tiempos de fallo (IV).
Comparación no paramétrica de muestras (V).
Tests de vida acelerada (VI).
Modelos de regresión para observaciones censuradas (VII).
Análisis Probit (Éxito / fracaso) (VIII).
MAPA CONCEPTUAL_________________________________________________
Función de
Supervivencia y
Tasa de Fallos
Tabla de Superv.
Fiabilidad (I):
Conceptos Básicos
Exponencial
Weibull
Distribuciones
habituales en fiabilidad
Lognormal
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
1
Conceptos básicos de Fiabilidad
INTRODUCCIÓN_____________________________________________________
Muchas de las técnicas que se presentan a lo largo de este trabajo, en especial las no paramétricas,
fueron inicialmente desarrolladas para su uso en estudios médicos y biológicos bajo el nombre
genérico de análisis de supervivencia (comparación de diferentes tratamientos médicos,
determinación de los factores que intervienen en la supervivencia de los peces de un río, etc.).
En la actualidad, sin embargo, la aplicación de dichas técnicas, en especial las paramétricas, se ha
extendido a otras áreas como la económica o la industrial bajo el nombre de análisis de tiempos de
fallo (establecimiento de períodos de garantía de un producto, diseño de planes de mantenimiento
preventivo, etc.).
La fiabilidad de un dispositivo (componente o sistema), sometido a unas condiciones de trabajo
concretas, es la probabilidad de que éste funcione correctamente (“sobreviva” sin fallar) durante un
determinado período de tiempo. Así pues, la fiabilidad constituye un aspecto fundamental de la
calidad de todo dispositivo. Por tal motivo, resulta especialmente interesante la cuantificación de
dicha fiabilidad, de forma que sea posible hacer estimaciones sobre la vida útil del producto.
Así, por ejemplo, en el caso de una avioneta monomotor, será de gran conveniencia conocer la
probabilidad de éste falle en diferentes etapas de su vida (tras 500 horas de funcionamiento, 800
horas de funcionamiento, etc.). El obtener una buena estimación de la fiabilidad del motor, posibilitará
la toma de decisiones racionales acerca de cuándo conviene revisarlo o cambiarlo por otro nuevo.
Hay una característica común a los datos que aparecen en la mayoría de los estudios sobre la
fiabilidad de un dispositivo, y es el hecho de que contengan observaciones censuradas:
supongamos que se lleva a cabo una investigación, de duración predeterminada, para analizar la
efectividad de un nuevo método de producción de bombillas. La variable de interés en este caso sería
el número de días que cada una de las bombillas “sobrevive” (funciona correctamente, sin fallos).
A primera vista, parecería sensato utilizar los métodos estadísticos tradicionales (tanto paramétricos
como no paramétricos) con objeto de describir el tiempo medio de supervivencia y comparar el nuevo
método de producción con los métodos anteriores. Sin embargo, al final de la investigación, es
probable que siga habiendo bombillas que funcionen correctamente, y el investigador no será capaz
de estimar con precisión cuánto tiempo más permanecerán sin fallar.
Para trabajar con este tipo de datos con información parcial no servirán pues los métodos
tradicionales, sino que serán necesarias técnicas específicas como las que presentamos en este
trabajo.
El math-block comienza con la definición de tres conceptos estadísticos básicos: función de
fiabilidad, vida media de un dispositivo, y tasa de fallo. Se clasifican después los distintos tipos de
observaciones censuradas, y se comenta el uso de los tests Chi-cuadrado para realizar contrastes
de hipótesis.
El documento concluye con la presentación de las tablas de supervivencia (un método clásico, no
paramétrico, que permite realizar estimaciones sobre los tiempos de fallo), y de algunas de las
distribuciones teóricas que más se utilizan en el análisis de la fiabilidad como son la exponencial, la
Weibull, y la lognormal.
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
2
Conceptos básicos de Fiabilidad
FUNCIÓN DE FIABILIDAD, VIDA MEDIA Y TASA DE FALLO_________________
Notación: en lo que sigue, se denotará por T a la variable aleatoria continua que describe los tiempos
de fallo de un determinado dispositivo, i.e.: T = “tiempo transcurrido hasta que se produce el fallo".
Denotando por f(t) a la función de densidad de probabilidad (f.d.p.) de T, y por F(t) a su función de
distribución (f.d.), se cumplirá:
b
P(a ≤ T ≤ b) = ∫ f (t )dt
a
t
F (t) = P(T ≤ t ) = ∫ f (u)du
0
f (t ) =
dF (t )
dt
Dado 0 < p < 1, por tp se denotará al cuantil p de F(t), i.e., tp será el menor instante temporal t tal que
F(t) = P( T ≤ t ) ≥ p .
•
La función de fiabilidad R(t) o función de supervivencia S(t), es la complementaria de
la f.d. de T, i.e., nos determina la probabilidad de que el dispositivo “sobreviva” al instante t
(esta función determina la proporción de dispositivos iniciales que seguirán funcionando
correctamente en el instante t):
S (t ) ≡ R(t ) = 1 − F (t ) = P(T > t )
•
Se llama vida media o tiempo medio hasta el fallo (Mean Time To Failure) de un
dispositivo a la esperanza de la v.a. T, i.e., la vida media determina el tiempo de duración
esperada de un dispositivo:
∞
MTTF = E [T ] = ∫ t f (t )dt
0
Cuando se consideren dispositivos reparables (que puedan seguir funcionando tras un
fallo), se hablará de tiempo medio entre fallos (MTBF).
•
Se define la tasa de fallo media en el intervalo (t1 , t2 ) como:
h(t1 , t 2 ) =
R(t1 ) − R(t 2 )
(t 2 − t1 ) R(t1 )
Observar que R(t1) – R(t2) representa la proporción de dispositivos totales que, habiendo
sobrevivido al instante t1 , han fallado en el intervalo (t1,t2). Al dividir esta diferencia por
R(t1) se obtiene la proporción de dispositivos supervivientes a t1 que han fallado en (t1,t2),
i.e.:
R(t1 ) − R (t 2 )
R(t1 )
es la probabilidad condicional de que un dispositivo que haya sobrevivido al instante t1
falle en el intervalo (t1,t2). Finalmente, al dividir por la longitud del intervalo, obtenemos la
proporción anterior (su media) por unidad de tiempo.
•
Haciendo tender t2 a t1, obtenemos la llamada tasa de fallo o tasa de riesgo:
R(t1 ) − R(t 2 ) − R ′(t1 ) F ′(t1 ) f (t1 )
=
=
=
t 2 →t 1 (t − t ) R (t )
R(t1 )
R(t1 ) R(t1 )
2
1
1
h(t1 ) = lim
La tasa de fallo puede pues interpretarse como la “velocidad” a la cual se producen los
fallos, i.e.: es una medida de lo propenso que resulta el dispositivo a fallar en función de
su edad.
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
3
Conceptos básicos de Fiabilidad
En la mayoría de los dispositivos electromecánicos, la función tasa de fallo tiene forma de
bañera: cuando se inicia la vida de un aparato, la tasa de fallo instantánea resulta ser
relativamente alta (es lo que se denomina "mortalidad infantil"); una vez que los componentes y
partes electromecánicas se han acoplado, la tasa de fallo es relativamente constante y baja
(etapa de “vida útil”); más adelante, tras un tiempo de funcionamiento, la tasa de fallo vuelve a
incrementarse hasta que, finalmente, todos los dispositivos habrán fallado (“efecto
envejecimiento”).
ETAPA VIDA
ÚTIL
T suele seguir
una distrib.
Exponencial o
Weibull
PERÍODO DE
DESGASTE
T suele seguir
una distribución
Weibull
Tasa de fallo
PERÍODO
INFANTIL
T suele seguir
aprox. una
distrib. Weibull
h(t)
Tiempo
Así, por ejemplo, muchos automóviles nuevos suelen presentar pequeños defectos de
funcionamiento al poco de comprarse (elevada tasa de fallos inicial). Una vez solventados tales
defectos, es de esperar que el vehículo proporcione un largo y complaciente período de
funcionamiento (baja tasa de fallos intermedia). Mas tarde, conforme pasan los años, el automóvil
se vuelve más propenso a sufrir averías hasta que, finalmente, después de 15 o 20 años,
prácticamente todos los vehículos están inservibles (elevada tasa de fallos final).
Observar que, a partir de la última ecuación, es posible expresar R(t) como función de h(t):
 dF (t ) 
dt 
1 dR(t )
f (t ) 
dR(t )
=
h(t ) =
=⋅
⇒ h(t )dt = R (t )
R(t )
R(t ) dt
R(t )
si ahora tomamos integrales a ambas partes:
t
t
0
0
∫ h(u )du = ∫
dR(u )
t
du = -[log R(u )]0 = - log R(t )
R(u )
de donde:
R(t ) = e

 t
 - h(u)du 

 0
∫
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
4
Conceptos básicos de Fiabilidad
OBSERVACIONES CENSURADAS______________________________________
Normalmente, los estudios de fiabilidad tienen una duración predeterminada, por lo que no todos los
dispositivos analizados habrán fallado a su conclusión. Por tanto, el investigador sabrá que un cierto
número de dispositivos han “sobrevivido” durante el período de tiempo que ha durado el test, pero
desconocerá el momento exacto en que hubieran fallado si el estudio se hubiese prolongado de
forma indefinida. Este tipo de datos se llaman observaciones censuradas.
Las observaciones de censura por tiempo o de tipo I aparecen al finalizar un test de duración
predeterminada: de los dispositivos “supervivientes” sólo se sabe que no han fallado hasta ese
momento. En este caso, el tiempo de duración del test es fijo, mientras que el número de productos
que fallan es una v.a.
Por contra, las observaciones de censura por fallos o de tipo II aparecen cuando el test continúa
hasta que una proporción predeterminada de dispositivos hayan fallado. Ahora, el número de
productos que fallan es fijo, siendo el tiempo de duración del test una v.a.
CENSURA TIPO II
CENSURA TIPO I
....
7
6
5
....
T5
4
3
2
1
7
6
5
t0
T6
t0
4
3
t0
2
1
T3
T1
El Dispositivo falla
t0
T6
T5
T3
T2
T1
Tiempo
Tiempo
CENSURA A DERECHA
CENSURA A IZQUIERDA
....
7
....
7
6
5
6
5
4
3
2
4
3
2
1
Tiempo
1
Tiempo
Fallo observado
Fallo NO observado
En los gráficos anteriores muestran los dos tipos de censura: en el primero, el experimento
termina cuando se llega al instante t0 ; en el segundo, el experimento termina cuando falla un
determinado porcentaje de dispositivos, en este caso 5.
Por otra parte, cuando la censura ocurre para un t > 0 (siendo t = 0 el instante en que se inicia el
test de fiabilidad) estaremos ante lo que se conoce como censura a la derecha. Podría ocurrir
también que la censura tuviera lugar para t < 0 (censura a la izquierda): por ejemplo, en una
investigación médica sobre el cáncer, se puede saber que el paciente ingresó en el hospital en
una fecha determinada (fecha de inicio del test), y que sobrevivió durante un intervalo temporal
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
5
Conceptos básicos de Fiabilidad
definido; sin embargo, probablemente no se conocerá cuándo aparecieron por primera vez los
síntomas de la enfermedad.
Se suele hablar de censura por intervalos o arbitraria para referirse a observaciones que han
sido censuradas tanto a derecha como a izquierda (es decir, de ellas sólo sabemos que entran
en la investigación cuando ésta ya estaba inicializada y salen de la misma, sin haber fallado,
antes de que finalice).
CENSURA ARBITRARIA O POR INTERVALOS
....
7
6
5
4
3
2
1
Tiempo
Fallo observado
Fallo NO observado
CENSURA SIMPLE
CENSURA MÚLTIPLE
....
7
6
....
7
6
5
4
5
4
3
2
1
3
2
1
Tiempo
Tiempo
Finalmente, se puede tener censura simple (si el experimento finaliza en el mismo instante para
todos los dispositivos observados), o censura múltiple. Un ejemplo de esta última sería cuando los
pacientes abandonan el hospital en instantes diferentes (bien por estar recuperados, bien por irse a
otro centro, etc.).
INTERPRETACIÓN DE LOS TESTS CHI-CUADRADO χ2 ____________________
En los próximos math-blocks se usará un test χ2 para contrastar la bondad del ajuste propuesto o
para contrastar diferencias entre grupos. Dado que las hipótesis del test serán diferentes según el
contexto en que estemos, también lo serán las conclusiones que se extraigan a partir del p-valor.
Un p-valor es estadísticamente significativo cuando sea menor o igual a una constante prefijada α.
Si así ocurre, se rechazará la hipótesis nula H0 en favor de la hipótesis alternativa H1. La constante α
representa la probabilidad condicional de rechazar la hipótesis nula, a partir de las observaciones, en
el supuesto de que esta hipótesis sea cierta (esto se conoce como error de tipo I). Por tal motivo,
interesa elegir un valor muy pequeño para α.
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
6
Conceptos básicos de Fiabilidad
Habitualmente se toma α = 0,05, con lo cual sólo en 5 de cada 100 casos en los que H0 sea cierta
será rechazada. Si se pretende ser aún más exigentes en cuanto a las “evidencias” que se han de
presentar para rechazar la hipótesis nula, se tomará α = 0,01 o bien α = 0,005. Observar, sin
embargo que, si bien escogiendo un α diminuto resulta más improbable un error de tipo I, también
resultará más probable cometer un error de tipo II, i.e.: que la hipótesis nula sea aceptada en las
ocasiones en que ésta sea falsa.
Fijar α= 0,05 ó 0,01 ó 0,005
según nivel de exigencia
α = Pr(rechazar H0
cuando H0 cierta)
NO rechazar H0
p-valor <= α?
Rechazar H0
2
Así, cuando se use un test χ para contrastar si las observaciones se pueden ajustar mediante una
distribución exponencial (i.e., para contrastar si los datos obtenidos podrían corresponder
“aproximadamente” a una v.a. que siguiese dicha distribución), el test será:
H0 : Las observaciones corresponden (aproximadamente) a una distrib. Exponencial
.
H1 : Las observaciones NO corresponden a una distrib. Exponencial
Obtener aquí un p-valor significativo implicará que la distribución utilizada no es buena para ajustar
los datos.
2
Si se recurre a un test χ
serán:
para contrastar posibles diferencias entre grupos muestrales, las hipótesis
H0 : Todos los grupos son (aprox.) iguales
H1 : Todos los grupos NO son iguales
Un p-valor significativo implicará aceptar la existencia de diferencias entre grupos.
2
Finalmente, un test χ para determinar la validez de un modelo de regresión será de la forma:
H0 : El modelo propuesto NO es mejor que el modelo nulo (i.e.: todos los coeficientes son cero)
H1 : El modelo propuesto es significativamente mejor que el nulo (i.e.: no todos los coeficientes
Si el test resulta significativo, se tendrá que al menos una de las variables explicativas del modelo
afecta al valor de la variable dependiente.
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
7
Conceptos básicos de Fiabilidad
TABLA DE SUPERVIVENCIA o ACTUARIAL_______________________________
Uno de los métodos no paramétricos más clásicos y directos para describir la fiabilidad de una
muestra es la tabla de supervivencia, la cual no es más que una tabla de frecuencias mejorada y
ampliada. A partir de ella es posible hacer una primera estimación sobre el comportamiento de la
función de supervivencia S(t), de la función de distribución F(t), de la función de densidad f(t), y de la
tasa de fallo h(t). El análisis del siguiente ejemplo, construido con ayuda de la hoja de cálculo Excel
(ver archivo TablaSup.xls ), permitirá entender su funcionamiento:
TABLA DE SUPERVIVENCIA (Life Table)
Inputs: Intervalos, dispositivos entranes, disp. censurados, y disp. fallados.
Nota: A fin de obtener estimaciones razonables, el número de dispositivos observados habrá de ser mayor de 30.
Intervalo
1
2
3
4
5
6
7
8
9
10
11
12
Dispositivos
Estimaciones
Inicio Int. Entrantes Censurados En Riesgo Fallados Prob. Fallo Prob. Superv.
R(t)
0,00
65
14
58,0
19
0,3276
0,6724
1,0000
161,36
32
4
30,0
4
0,1333
0,8667
0,6724
322,73
24
4
22,0
0
0,0227
0,9773
0,5828
484,09
20
4
18,0
1
0,0556
0,9444
0,5695
645,45
15
1
14,5
1
0,0690
0,9310
0,5379
806,82
13
3
11,5
1
0,0870
0,9130
0,5008
968,18
9
1
8,5
2
0,2353
0,7647
0,4572
1129,55
6
1
5,5
0
0,0909
0,9091
0,3496
1290,91
5
1
4,5
1
0,2222
0,7778
0,3179
1452,27
3
2
2,0
0
0,2500
0,7500
0,2472
1613,64
1
0
1,0
0
0,5000
0,5000
0,1854
1775,00
1
1
0,5
0
1,0000
0,0000
0,0927
1,00
0,0020
0,80
Probabilidad
Probabilidad
0,0025
0,0015
0,0010
0,0005
0,0000
2
3
4
5
6
7
8
9
0,60
0,40
0,20
0,00
10 11
1
2
3
4
5
Intervalo
Tasa de Riesgo
Probabilidad
0,80
0,60
0,40
0,20
0,00
3
4
5
6
7
Intervalo
7
8
9
10 11
Tasa de Riesgo h(t)
1,00
2
6
Intervalo
Función de Supervivencia R(t)
1
h(t)
0,0024
0,0009
0,0001
0,0004
0,0004
0,0006
0,0017
0,0006
0,0015
0,0015
0,0031
---
f.d. F(t)
f.d.p. f(t)
1
f(t)
0,0020
0,0006
0,0001
0,0002
0,0002
0,0003
0,0007
0,0002
0,0004
0,0004
0,0006
---
8
9
10
11
0,0040
0,0030
0,0020
0,0010
0,0000
1
2
3
4
5
6
7
8
9
10 11
Intervalo
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
8
Conceptos básicos de Fiabilidad
La distribución de los tiempos de supervivencia (o tiempos de fallo) se divide en un determinado
número de intervalos. Se denotará por (ti-1, ti] al i-ésimo intervalo. Para cada intervalo se registra el
número de observaciones o dispositivos que han entrado en buen estado ni (entrantes), el número de
los que han fallado en él di (fallados), y el número de observaciones perdidas o censuradas en él ri
(censurados).
A partir de estos datos, es posible calcular otros estadísticos adicionales que se describen a
continuación:
•
Número de observaciones en riesgo n’i : es el nº de observaciones que entró en el
intervalo respectivo en buen estado, menos la mitad del nº de observaciones perdidas o
censuradas en dicho intervalo:
r
ni′ = ni − i
2
•
Probabilidad de fallo: para cada intervalo, es la proporción de observaciones en riesgo que
fallan. En el caso de que un intervalo no registre ningún fallo, se acostumbra a tomar 0,5 en
lugar de 0 a la hora de contabilizar el número de fallos (a fin de “suavizar” las funciones
estimadas):
ˆi =
p
•
di
n'i
Probabilidad de supervivencia: es la proporción de observaciones en riesgo que
sobreviven (1 – probabilidad de fallo):
ˆi = 1 − p
ˆi
q
•
Función de supervivencia: para cada intervalo, es la proporción de observaciones que han
logrado llegar hasta él en buen estado. Se calcula multiplicando la proporción de
supervivientes de todos los intervalos anteriores (se supone que los fallos en un intervalo son
independientes de los anteriores):
ˆ =S
ˆ(t ) =
S
i
i −1
•
i −1
∏ (1 − pˆ j )
j =1
Función de densidad de probabilidad (f.d.p.): para cada intervalo, es una estimación de la
probabilidad de fallo por unidad de tiempo. Para calcularla, primero se halla la diferencia entre
la proporción de dispositivos supervivientes al inicio del intervalo y la proporción de
supervivientes al final del intervalo. El valor que obtenido se dividirá por la longitud del
intervalo:
ˆ −S
ˆ
S
i +1
ˆ
fi = i
t i − t i −1
•
Tasa de fallo o de riesgo: es la probabilidad, por unidad de tiempo, de que un dispositivo
que haya sobrevivido hasta el inicio del intervalo falle en él. Para hallarla, primero se
calculará el cociente entre el nº de fallos (usando 0,5 cuando éste sea 0) y la longitud del
intervalo. El resultado obtenido se dividirá por la media entre el número de dispositivos
entrantes en dicho intervalo y el número de dispositivos entrantes en el intervalo siguiente:
di
ˆ =
h
i
•
(t i t i 1 )
(ni + ni +1 ) / 2
A fin de obtener estimaciones razonables de la función de supervivencia, de la función de
densidad de probabilidad, y de la función tasa de fallo, será necesario disponer de, como
mínimo, 30 observaciones completas (no censuradas).
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
9
Conceptos básicos de Fiabilidad
DISTRIBUCIONES HABITUALES EN FIABILIDAD__________________________
La tabla de supervivencia proporciona una visión descriptiva de cómo se distribuyen los tiempos de
fallo. Sin embargo, para poder realizar predicciones probabilísticas será necesario conocer cual es
(aproximadamente) la distribución de la población que subyace tras las observaciones.
Sea T la variable que representa los tiempos de fallo de un determinado dispositivo ( T > 0 ). El
objetivo será conocer (si ello es posible) la función de distribución asociada a T, la cual será de la
forma F( t ; θ) = P( T ≤ t ) , siendo θ un vector de parámetros.
En general, la mayoría de distribuciones usadas en fiabilidad tienen, a lo sumo, tres parámetros:
•
Parámetro de escala α: este es el parámetro que caracteriza a las distribuciones
unipararamétricas. El parámetro de escala define cuán dispersa se encuentra la distribución
(en el caso de la distribución normal, el parámetro de escala es la desviación típica).
•
Parámetro de forma β: este parámetro define la forma de la distribución. Algunas
distribuciones (como la exponencial o la normal) carecen de este parámetro pues tienen una
forma predeterminada que nunca varía (en el caso de la normal, ésta tiene siempre forma de
campana).
•
Parámetro de localización γ: se usa para desplazar una distribución hacia un lado u otro.
Esto significa que, dada una distribución cuyo dominio habitual sea [0 , +∞), la inclusión de un
parámetro de localización γ cambiará el dominio a [γ , +∞). En el caso de la normal, el
parámetro de localización es la media.
Se dice que una v.a. Y pertenece a la familia localización-escala (location-scale) si su f.d. se puede
expresar de la forma:
F(y; µ, σ) = P(Y ≤ y) =
Φ y σ- µ 


donde Φ no depende de ningún parámetro desconocido. En tal caso, µ ∈ (-∞ , +∞) es el
parámetro de localización, y σ > 0 es el parámetro de escala.
Observar que Φ es la f.d. de la v.a. Z = (Y - µ)/σ . Muchas de las distribuciones más habituales, o bien
pertenecen a esta familia o bien están íntimamente relacionadas. Ejemplos de distribuciones que
pertenecen a esta familia son la normal, la logística, y la de valores extremos:
Normal Æ
F( y;µ, σ) = Φ nor
Logística Æ
µ
y
F( y; µ, σ) = Φ logis
σ
donde Φnor es la f.d. de una N(0,1)
y µ
σ
donde Φlogis (z) = exp(z) / (1 + exp(z))
Se dice que una v.a. T pertenece a la familia log-localización-escala si Y = log(T) es un miembro de la
familia localización-escala. Ejemplos de distribuciones que pertenecen a esta familia son la
exponencial, la Weibull, la log-normal, y la log-logística:
 log(t)
LogNormal → F(t; µ, σ) = Φ nor 
σ

 log(t)
Log log ística → F(t; µ, σ) = Φ log is 
σ

 log(t)
Weibull → F(t; µ, σ) = Φ ve 
σ

µ


µ


µ
 donde Φve (z) = 1 – exp{-exp(z)}

Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
10
Conceptos básicos de Fiabilidad
Las distribuciones que más se emplean a la hora de modelar tiempos de fallo, algunas de las cuales
serán comentadas a continuación, son la Weibull, la exponencial, la normal, la log-normal, la logística,
la log-logística, y la de valores extremos.
Distribución Exponencial: se utiliza para modelar el tiempo transcurrido entre dos sucesos
aleatorios no muy frecuentes cuando la tasa de ocurrencia, λ , se supone constante.
En fiabilidad se usa para describir los tiempos de fallo de un dispositivo durante su etapa de vida útil,
en la cual la tasa de fallo es (aproximadamente) constante, i.e.: h(t) = λ . Una tasa de fallo constante
significa que, para un dispositivo que no haya fallado con anterioridad, la probabilidad de fallar en el
siguiente intervalo infinitesimal es independiente de la edad del dispositivo.
La tasa de fallo λ es el parámetro que caracteriza a esta distribución. Este valor es la inversa del
tiempo medio que transcurre hasta el fallo (o entre dos fallos consecutivos, MTBF, si el dispositivo
sigue funcionando), i.e.: α = MTTF = 1/λ . Observar que aquí α es el parámetro de escala, también
llamado vida característica. La f.d.p. de una distribución exponencial es de la forma:
f(t) = λ ⋅ exp{− λ ⋅ t}
0 < t < ∞, λ > 0
f.d.p. de una Exponencial
f.d. de una Exponencial
1,0
0,25
lamda = 0,250
lam da = 0,250
0,15
F(t)
f(t)
0,20
0,10
lamda = 0,125
0,5
lamda = 0,125
0,05
0,0
0,00
0
50
0
100
50
100
t
t
Función de Supervivencia de una Exponencial
Tasa de Riesgo de una Exponencial
1,0
0,25
0,5
h(t)
S(t)
lamda = 0,250
lam da = 0,125
0,20
lam da = 0,250
lam da = 0,125
0,15
0,0
0
50
t
100
0
50
100
t
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
11
Conceptos básicos de Fiabilidad
Una generalización de la distribución anterior sería la distribución exponencial bi-paramétrica, cuya
f.d.p. es de la forma:
1

exp
α

f(t; α, γ) =
t
γ
 ,
α 
donde α = 1/λ > 0 es el parámetro de escala, y γ es el parámetro de localización. Notar que cuando γ
= 0 se obtiene la distribución exponencial de un único parámetro.
Distribución de Weibull: Se ha comentado antes que la distribución exponencial es utilizada a
menudo para modelar los tiempos de fallo cuando la tasa de riesgo es constante. Si, por el contrario,
la probabilidad de fallo varía con el tiempo resulta más apropiada una Weibull (de hecho la
exponencial puede verse como un caso particular de la Weibull).
La Weibull es tan flexible que, eligiendo adecuadamente sus parámetros, permite describir las tres
etapas de la función tasa de fallos (curva de la bañera). Esta distribución viene caracterizada por dos
parámetros: α (escala) y β (forma). Su f.d.p. es:
f (t) =
β t
⋅ 
α α
β −1
  t β 
⋅ exp−   
  α  
Observar que cuando β =1, basta con tomar
exponencial.
0<t<∞ , α>0 , β>0
α = 1/λ
f.d.p. f(t) Weibull para escala = 10
para obtener la f.d.p. de la distribución
f.d. F(t) Weibull para escala = 10
1,0
0,15
forma = 1
forma = 4
0,10
F(t)
f(t)
forma = 1
0,5
forma = 2
forma = 2
0,05
forma = 4
0,0
0,00
0
10
0
20
10
20
t
t
Tasa Riesgo h(t) Weibull para escala = 10
Función Supervivencia Weibull para escala = 10
0,4
1,0
forma = 4
forma = 4
0,5
h(t)
R(t)
0,3
forma = 2
forma = 1
forma = 1
0,2
forma = 2
0,1
0,0
0,0
0
10
t
20
0
5
10
t
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
12
Conceptos básicos de Fiabilidad
Distribución Lognormal: La f.d.p. de una distribución normal es no nula en todo el eje real (y no
sólo en el semieje positivo). Por este motivo, el uso de la normal implicaría que el fallo puede
producirse antes del instante t = 0. Para evitar esta inconveniencia que presenta la distribución
normal, se puede utilizar en su lugar la distribución Log-normal.
Se dice que una variable aleatoria T sigue una distribución Lognormal (base e), de parámetros γ
(localización) y α (escala), cuando su logaritmo neperiano Y = Log(T) se distribuye de forma normal
con media γ y desviación típica α.
Y
Inversamente, dada una v.a. Y≈N(π,σ), la variable aleatoria T = e seguirá una distribución
Lognormal (base e) de parámetros γ = µ (localización) y α = σ (escala), cuya f.d.p. será:
f(t) =
1
 −1
(ln(t) − µ )2 
⋅ exp 
2
σ ⋅ t 2π
 2σ

f.d.p. f(t) Lognormal para mu = 0
t>0
f.d. F(t) Lognormal para mu = 0
1,5
1,0
sigma = 0,3
sigma = 0,3
1,0
f(t)
F(t)
sigma = 1
sigma = 0,1
0,5
sigma = 0,5
0,5
sigma = 1
0,0
0,0
0
1
2
3
4
5
0
1
3
4
5
t
Función Supervivencia Lognormal para mu = 0
Tasa Riesgo h(t) Lognormal para mu = 0
1,0
sigma = 0,3
4
h(t)
3
R(t)
2
t
sigma = 0,1
0,5
sigma = 0,3
sigma = 0,1
2
sigma = 1
sigma = 1
1
0,0
0
0
1
2
3
t
4
5
0
1
2
3
4
5
t
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
13
Conceptos básicos de Fiabilidad
BIBLIOGRAFÍA______________________________________________________
[1]
Arsenault, J.E.; Roberts, J.A.(1980): Reliability and maintainnability of electronic systems.
Computer Science Press.
[2]
Ascher, H.; Feingold, H. (1984), Repairable systems reliability. Dekker.
[3]
Barlow & Proshan (1981). Statistical theory of reliability and life testing. To begin with.
[4]
Breuer, M.A.; Friedman, A.D (1976), Diagnosis and reliable design of digital systems.
Computer Science Press.
[5]
García Muñoz R., Quiles Flor F (1992), Fiabilidad y Test de Sistemas. Depto Informática
Albacete, UCLM.
[6]
Sundararajan, C.R. (1991), Guide to reliability engineering. VNR.
[7]
Trivedi (1982). Probability and statistics with reliability, queueing and computer science
applications. Ed. Prentice Hall.
[8]
Warleta, J. (1973), "Fiabilidad. Bases teóricas y prácticas". INTA.
[9]
Zacks (1992). Introduction to reliability analysis. Ed. Springer Verlag.
ENLACES___________________________________________________________
[W1]
Desde la página de la empresa española ISDEFE podemos bajarnos dos libros de la serie
azul de las monografias. El primero de ellos es Fiabilidad de Joel A. Nachlas.
así como también el libro Mantenibilidad de Jezdimir Knezzevic.
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
14
Conceptos básicos de Fiabilidad
ambos son excelentes introduciones al tema.
[W2]
Antonio Ángel Blesa de la Universidad de Las Palmas de Gran Canaria ha elaborado un
excelente Tutorial sobre fiabilidad.
Proyecto e-Math
Financiado por la Secretaría de Estado de Educación y Universidades (MECD)
15