funciones actividad

Actividad
1. Identifique cuál de los siguientes diagramas sagitales representan una función. Para
ello, marca si o no según corresponda.
a)
f
b)
g
-1
1
0
0
0
10
0,5
0,5
10
0
1
1
25
11
1,5
1,5
NO
SI
NO
SI
2. Calcula el valor de cada expresión. Para ello, reemplaza los valores correspondientes
en cada caso.
x 1
f(x) = 2x – 2
g(x) = x2
h(x) =
2
a. f(-2) + g(3) + h(0,5)
b.
g(0) + g(10) – f(6) + h(1) =
c.
d.
1
2
h   - g   + f(4) =
2
3
2
f(-4) + 3(1,3) – g   + f
3
1
  =
2
3. Evalúa si cada afirmación es verdadera (V) o falsa (F). Para ello, escribe V o F según
corresponda.
a.
Si f(x) = x3, entonces se cumple que f(1) – f(-1) = f(0)
b.
Si f(x) = 1 – x, se tiene que la imagen de 100 es -99
c.
Si h(x) = 5, entonces la preimagen de 5, es 25.
4. Relaciona cada función de la columna A con el dominio que le
corresponde en la columna B.
Columna A
Columna B
f(x) = 3x – 5
Dom (f) = R – {1}
x4
x 1
2
f(x) =
x4
x 8
f(x) =
( x  1)( x  4)
Dom (f) = R - {1, -4}
f(x) =
f(x) =
Dom (f) = R - {9}
Dom (f) = R
x5
9 x
Dom (f) = R - {4}
5. Analiza la siguiente función. Luego, responde.
f(x) =
5 x
x
a. ¿Cuál es la preimagen de 5?
b. ¿Cuál es preimagen de 0? ¿ Y la imagen de 0?
c. ¿Qué puedes concluir con respecto al dominio y al recorrido de f?
6. Analiza el siguiente ejemplo. Luego, responde
1
x  3x  2
basta con excluir del conjunto los puntos en donde no está definida, es decir,
x2 + 3x + 2 = 0, ya que no está definido. Por lo tanto, factorizando el
1
denominador, la función se puede representar f(x ) =
De esta
( x  1)( x  2)
Ejemplo: para determinar el dominio de la función f(x) =
2
manera, Dom f(f) = R – {-1, -2}
a. f(x) =
3 x
, Dom (f) = R - {
x  6x  9
b. g(x) =
x5
x  4x
}
2
2
, Dom(g) = R – {
}
Función lineal y función afín.
1. Analiza cada gráfico e identifica cuál es función afín. Después, escríbelo en cada
recuadro según corresponda.
Y
a.
2Y
1
1
-2
-1
0
1
2
-2
-1
-2
-1
0
1
2
-1
-2
-2
Función
Función
1
-2
-1
0
1
2
-1
Función
2. Identifica cada función , luego marca con una X si la función es lineal o afín
a. f(x) = 3x
Lineal
Afín
b. g(x) = 2x + 5
Lineal
Afín
c. h(x) =
Lineal
Afín
Afín
d. f(x) =
Lineal
Afín
e. g(x) =
Lineal
Afín
-1
f. h(x) =
Lineal
Afín
3. Calcula la constante de proporcionalidad asociada a cada función. Luego, grafícala en
el plano cartesiano correspondiente.
a. f(x) = -3x
k=
Y
X

b. f(x) = -
Utiliza el gráfico hecho en a. y grafica la función g(x) = -3x + 5
3
x
9
k=
Y
X
 Utiliza el gráfico hecho en a. y grafica la función g(x) = -3x + 5.
4. Representa algebraicamente y en el plano cartesiano una función afín de modo que
los puntos dados pertenezcan el gráfico de la función.
a. (0,2) y (2, 4)
Y
X
f(x) =
b. (5, 0) y (0, 5)
Y
X
g(x) =
5. Representa las siguientes funciones en un plano cartesiano y clasificalas en función
lineal o función afín.
a. f(x) = 2x - 1
Y
X
b. g(x) = -4x
Y
X
6.Resuelve los siguientes problemas.
a. En una panadería se gana $45 por cada pan vendido. Además, diariamente en la
panadería se estima una ganancia fija de $100.000 por las ventas de otros
productos. Expresa la ganancia G en un día con respecto a la venta x panes
b. En una librería se vende un libro en $15.500. Si debido a la poca demanda se baja
su precio en un 20%, ¡qué función D permite calcular el dinero recibido por la
venta de x libros luego de su rebaja
Otros tipos de funciones
1. Calcula el valor de cada expresión. Para ello, reemplaza los valores correspondientes
en cada caso.
f(x) = [x – 3]
g(x) = | x + 5|
h(x) = -
5
2
a.
5
f(1) + g(-5) + h  
2
c. 10f(3)+g(-10)-h(1.000)=
b.
-g(10)+4g(0)-f(13)+2h(0)
 1  5  1 
d. f(5)+2h   -g   +f   =
 2 3 3
2. Evalúa si cada afirmación es verdadera (V) o falsa (F). Para ello escribe V o F según
corresponda
Si f(x) = x3, entonces se cumple que f(1) – f(-1) = f(0)
a.
Sea f(x) = 12x+81, entonces se cumple que f(0) + f(2) = f(-4)
b.
Si g(x) = [1-x] la imagen de 0,5 es 0
c.
Si h(x) = x la imagen del |-5,5|, es -5,5
d.
Si p(x) = [x] + 3 la imagen de 3, es 9.
3. Analiza cada una de las siguientes funciones. Luego, grafícales en el plano cartesiano.
a. f(x) = [x + 5]
Y
X
b.
h(x) = |x|-1
Y
X
4. Analiza los enunciados. Luego, completa la tabla y modela cada situación con una
función.
a. La cuenta de agua se calcula considerando $566 de cargo fijo y $550 por metro cúbico
(m2). Se cobra sobreconsumo cuando se gasta más de 40 m3; en ese caso, el metro
cúbico sube a $650.
Consumo
(m3)
Costo
($)
30
35
40
45
50
55
60
b. Un estacionamiento cobra $20 pesos por cada minuto de uso.
Tiempo
(minutos)
Costo($)
1
2
3
4
5
6
7
c.
En una pizzería se cobró un consumo mínimo de $3.500, lo que da derecho a comer
todos los trozos de pizza que de desee.
Trozos
de
pizza
Costo
($)
1
2
3
4
5
6
Composición de funciones y transformaciones isométricas
1. Analiza cada caso. Luego, responde
Sean f: R
R y h: R
R, funciones definidas por: f(x) = 4x + 1, g(x) = [x] + 9 y
1
h(x) = - |x|.
2
a. Determina las expresiones algebraicas que representan a;
(f ◦ f)(x), (f ◦ g)(x), (h◦ f)(x) y (g ◦ g)(x)
b. Calcula el valor de (f ◦ (h ◦ h)(0,5)
2. Calcula el valor de cada expresión. Para ello, remplaza los valores indicados.
Sean g y f, funciones
1
si x  - 1
3
g(x) =
x  1 si  - 1
h(x) =
si x  - 1
x
a. (h ◦ g)(2) =
d. (g ◦ (g ◦ h)(0) =
b.
e. (g◦(h◦h))(-24) =
(g ◦ h)(-9) =
c. (g◦g)(-7) =

[ x]  1 si x  - 1
f. (h◦g)(0,2) =
Grafica de función g
Y
X

Grafica la función h.
Y
X
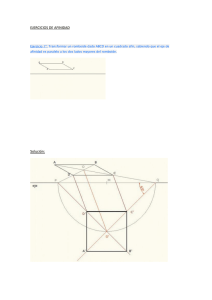
2. Analiza las siguientes transformaciones isométricas. Luego, responde.
a.¿Qué transformación isométrica se
aplicó a la figura 1 para 0btener
como imagen la figura 2?
Figura 2
3.Figura
1
2
Figura 3
Figura
4
b.¿Qué composición de
4.
transformaciones
isométricas
permite obtener como imagen la
figura 3 a partir de la figura 1?
c.¿Qué
composición
de
transformaciones
isométricas
permite obtener como imagen la
figura 4 a partir de la figura 1?
5. Representa en el plano cartesiano las situaciones pedidas.
a. Construye el triángulo ABC de vértices a(1,2), B(3,3) y C(2,4).
siguiente transformación: (R(0270°) ◦ Tῡ ), donde ῡ = (2,-1)
Luego aplica la
Y
X
b. Construye el cuadrilátero DEFG de vértices: D(0,0=, E(2,-1); F(3,1) y G(5,3). Luego,
aplica la siguiente transformación: (R(0,90°) ◦ Tṽ◦ Ry), donde ṽ = (-1, 3)
Y
X
Evaluación
Lee atentamente y marca la alternativa correcta.
1. Si f(x) = -3x +2, ¿cuál es la imagen de -5?
A. 10
B. 17
C. -6
D. -13
E. -17
2. El perímetro de una circunferencia de radio r se calcula según la fórmula P(r) = 2πr.
Si se considera π = 3, ¿cuál es el perímetro de la semicircunferencia de radio 4 cm?
A. 6 cm
B. 12 cm
C. 20 cm
D. 24 cm
E. 30 cm
3. De los siguientes gráficos.
I
2
II
Y
2Y
1-
1
0
-2
-1
X
0
0
1
2
1
III.
1-
0
-2
-1
X
0
1
¿Cuál (es) NO representa (n) una función
A.
B.
C.
D.
E.
Solo I
Solo II
Solo III
Solo I y II
Solo II y III
4. En relación con la función y = 8 – x, ¿qué afirmación es VERDADERA?
A. Cuando x = 1, y = 8
B. Es una función lineal
C. El punto (9,1) pertenece a su gráfico
D. El dominio de la función es el conjunto de los números reales
E. Ninguna de las anteriores
5. El dominio de la función g(x) =
x 1
es
x
A. IR
B. IR – {0}
C. IR – {1}
D. IR – {0,1}
6.¿Cuál es el dominio de la función g(x) =
x8
x  5x  6
2
X
0
1
A. IR – {2,3}
B. IR – {-2,-3}
C. IR –{-5,6}
D. IR – {2,3,-8}
E. IR – {-2.-3.8}
7. Considerando el siguiente diagrama sagital
f
-1
5
0
10
7
25
¿Cuál es el recorrido de la función?
A. {5}
B. {5,7}
C. {5, 7, 8}
D. {-1, 0,10,25}
E. {-1, 0, 5, 7, 10, 25}
8.Con respecto a la siguiente tabla:
x
g(x)
5
-5
1
-1
0
0
-1
1
-2
2
-3
3
-4
4
¿Qué función cumple con los valores de la tabla?
A.
B.
C.
D.
E.
Una función afín
Una función lineal
Una función identidad
Una función constante
Una función valor absoluta
9. De las siguientes funciones:
x 1
5
x
II. g(x) =
5
III. h(x) = x
I. f(x) =
¿Cuál (es) es (son) lineal (es)?
A. Solo I
B. Solo II
C. Solo I y II
D. Dolo II y III
E. I, II y III
10.El consumo de combustible depende de la cantidad de kilómetros recorridos por un
automóvil. Si este consume un litro cada 14 km recorridos, la situación se puede
modelar mediante una:
A. Función afín
B. Función lineal
C. Función identidad
D. Función constante
E. Función valor absoluto
11. ¿En qué punto del plano cartesiano la función f(x) = 3x – 6 intersecta al eje X?
A. {3,0}
B. {6, 0}
C. {2,0}
D. {1,- 6}
E. {1, -2}
12. ¿Cuál de los siguientes puntos del plano cartesiano pertenece a la función g(x) =
A.
(3,0)
B. (0,3)
5 
C.  ,3 
2 
5x
+3?
2
 5
D.  3, 
 2
E. Ninguna de las anteriores
13. ¿Cuál de las siguientes características representa al gráfico de la función identidad?
A.
B.
C.
D.
E.
Una recta paralela al eje X
Una recta paralela al eje Y
Es una función lineal con pendiente -1
Una recta que pasa por el origen (0,0)
Ninguna de las anteriores.
14. Una tienda comercial realiza la siguiente promoción. “Por cada año que el cliente tenga
se realizará el mismo porcentaje de descuento al precio de venta; así, el cliente tiene 20
años, se realizará un 20% de descuento” ¿Qué tipo de función te permitiría
representar el precio de venta?
A. Función afín
B. Función lineal
C. Función constante
D. Función identidad
E. Función valor absoluto
15. ¿Cuál (es) de las siguientes afirmaciones es (son) VERDADERA (S)?
I. La función identidad es SIEMPRE de la forma f(x) = x
II. El recorrido de la función valor absoluto f(x) = |x| es IR+ U {0}
III.El gráfico de la función constante siempre intersecta al origen (0, 0)
A.
B.
C.
D.
E.
Solo I
Solo I y II
Solo I y III
Solo II y III
Ninguna de las anteriores
16. Si f(x) = 2x + 3 y g(x) = 5x – 4, ¿qué alternativa representa (f ◦ g)(x)?
A. 7x – 1
B. 10x – 5
C. -3x – 1
D. 10x – 12
E. 10x2 + 7x – 12
17. Si f es una función constante, ¿cuál es la imagen de 3?
(1) f(x) = 4
(2) (5,4) pertenece al gráfico de la función
A. (1) por sí sola
B. (2) por sí sola
C. Cada una por sí sola, (1) o (2)
D. Ambas juntas (1) y (2)
E. Se requiere información adicional
18. Sea f una función afín. ¿Qué expresión algebraica representa a la función f(x)?
(1) La recta pasa por el punto (0,3)
(2) La recta pasa por el punto (4, 8)
A.
B.
C.
D.
E.
(1) por sí sola
(2) por sí sola
Cada una por sí sola, (1) o (2)
Ambas juntas, (1) y (2)
Se requiere información adicoinal