2.1.PRUEBA DE HIPÓTESIS PARA LA MEDIA DE UNA POBLACIÓN(*)

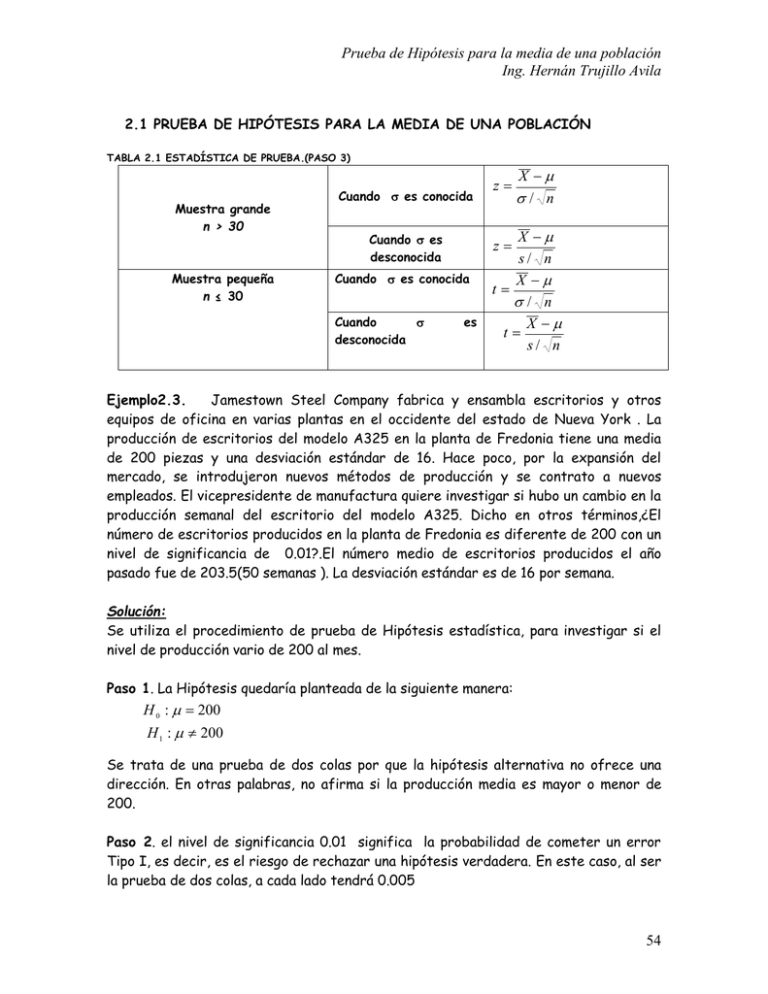
Prueba de Hipótesis para la media de una población
Ing. Hernán Trujillo Avila
2.1 PRUEBA DE HIPÓTESIS PARA LA MEDIA DE UNA POBLACIÓN
TABLA 2.1 ESTADÍSTICA DE PRUEBA.(PASO 3)
Muestra grande
n > 30
Muestra pequeña
n ≤ 30
Cuando  es conocida
Cuando  es
desconocida
X 
/ n
X 
s/ n
X 
t
/ n
X 
t
s/ n
z
Cuando  es conocida
Cuando

desconocida
z
es
Ejemplo2.3.
Jamestown Steel Company fabrica y ensambla escritorios y otros
equipos de oficina en varias plantas en el occidente del estado de Nueva York . La
producción de escritorios del modelo A325 en la planta de Fredonia tiene una media
de 200 piezas y una desviación estándar de 16. Hace poco, por la expansión del
mercado, se introdujeron nuevos métodos de producción y se contrato a nuevos
empleados. El vicepresidente de manufactura quiere investigar si hubo un cambio en la
producción semanal del escritorio del modelo A325. Dicho en otros términos,¿El
número de escritorios producidos en la planta de Fredonia es diferente de 200 con un
nivel de significancia de 0.01?.El número medio de escritorios producidos el año
pasado fue de 203.5(50 semanas ). La desviación estándar es de 16 por semana.
Solución:
Se utiliza el procedimiento de prueba de Hipótesis estadística, para investigar si el
nivel de producción vario de 200 al mes.
Paso 1. La Hipótesis quedaría planteada de la siguiente manera:
H 0 :   200
H 1 :   200
Se trata de una prueba de dos colas por que la hipótesis alternativa no ofrece una
dirección. En otras palabras, no afirma si la producción media es mayor o menor de
200.
Paso 2. el nivel de significancia 0.01 significa la probabilidad de cometer un error
Tipo I, es decir, es el riesgo de rechazar una hipótesis verdadera. En este caso, al ser
la prueba de dos colas, a cada lado tendrá 0.005
54
Prueba de Hipótesis para la media de una población
Ing. Hernán Trujillo Avila
Paso 3. La estadística de prueba para una media de muestra grande es:
z
X 
/ n
note que en este problema estamos tomando a 200 como la producción semanal, por lo
tanto el valor 16 sería  y no s.
Paso 4. Se formula una regla de decisión en base al valor crítico de z encontrado en
tablas. Como se trata de una prueba de dos colas, la mitad de 0.01, es decir 0.005
está en cada cola. De este modo, al utilizar las tablas buscamos el valor que
corresponde al área bajo la curva de 0.4950, y vemos que es 2.58
Paso 5. Se toma la muestra de la población (producción semanal), se calcula z, y se
aplica la regla de decisión, es decir se acepta o se rechaza H0.
de este modo
z
203.5  200
 1.55
16 / 50
Por lo tanto Se Acepta la hipótesis originalmente planteada ya que el valor 1.55 cae
dentro de la zona de aceptación, por lo cual se puede informar al vicepresidente de
manufactura que la evidencia de la muestra, no indica que el nivel de producción en la
planta de Fredonia haya cambiado del nivel de 200 unidades por semana
55
Prueba de Hipótesis para la media de una población
Ing. Hernán Trujillo Avila
El nivel de significancia observado o valor p
Por lo regular, solo se rechazará la hipótesis nula si el nivel de significancia observado
es menor al nivel de significancia  fijado en el paso 2.
Es el área dado en
tablas para z = 1.55
Para el ejemplo anterior:  = 0.01
Valor p = P(z ≥ 1.55 ) = 0.5 – 0.4394 = 0.0606
Como en este caso la prueba es de dos colas, p = 0.0606 *2 = 0.1212
Como p >  , la hipótesis nula no se Rechaza
Ejemplo 2.4. The processors of Fries’ Catsup indicate on the label that the bottle
contains 16 ounces of catsup. A sample of 36 bottles is selected hourly and the
contents weighed. Last hour a sample of 36 bottles had a mean weight of 16.12
ounces with a standard deviation of .5 ounces. At the .05 significance level is the
process out of control?
• Step 1: State the null and the alternative hypotheses:
H 0 :   16
•
•
H1 :   16
Step 2: The significance level is .05.
Step 3: Compute the value of the test statistic:
z  [16.12 16] /[.5 / 36 ]  1.44
•
Step 4: State the decision rule:
H 0 is rejected if z  1.96 or z  1.96
•
Step 5: Decide on H0 : H0 is not rejected because 1.44 is less than the critical
value of 1.96
Ejemplo 2.5.Las pescaderías de Wyoming sostienen que el número promedio de
truchas capturadas durante todo un día de pesca con señuelos es de 4.0. Para hacer su
actualización anual, el personal de pescadería pidió a una muestra de pescadores que
llevaran la cuenta del número de capturas diarias. Los números fueron:
4,4,3,2,6,8,7,1,9,3,1 y 6. Con un nivel de significancia de 0.05 ¿Existen evidencias
suficientes para suponer que ha aumentado el número de capturas diarias?
Paso 1. Aunque la pescadería afirma que el total de truchas es igual a 4, Para un buen
estudio, conviene probar si estas están por arriba o por de bajo de esta cantidad.
H0 : µ ≤ 4
H1: µ > 4
prueba de una sola cola
56
Prueba de Hipótesis para la media de una población
Ing. Hernán Trujillo Avila
Paso 2. 0.05
Paso 3. como n=12 ( muestra pequeña), y no se conocen los parámetros de la población:
t
X 
s/ n
Paso 4.Como la prueba es de una sola cola, se busca el valor de t para 0.05 nivel de
significancia y para 11 grados de libertad: 1.796
Paso 5. procesando los datos recabados; en la calculadora se obtiene una media
muestral de 4.5 y una desviación estándar muestral de 2.68
t
4.5  4
 0.646
2.68 / 12
Por lo tanto se Acepta H0. lo que implica que no se ha demostrado el aumento en la
cantidad de truchas capturadas, es decir que sea mayor a 4.
Utilizando el valor p
A diferencia de la tabla de áreas bajo la curva normal, la tabla de distribución t de
Student solo da valores de t que corresponden a las áreas .1 ,.05, .025, .010, .005,
.001 y .0005. Por lo tanto, solo podemos aproximar el valor p de la prueba. Como el
valor t observado se basó en 11 grados de libertad, utilizamos la fila g.l. = 11 y
avanzamos por esa fila hasta llegar a los valores de t más cercanos al valor observado
t = 0.646, en en este caso tomamos t0.10
Por lo tanto valor p = 0.10 > 0.05 , no se Rechaza, Se Acepta H0.
UTILIZANDO SPSS
SPSS prueba la Hipótesis haciendo mediante el cálculo del valor p.
Como ya mencionamos anteriormente, si p <  , H0 se Rechaza; por lo tanto si p > 
se Acepta H0.
SPSS solo proporciona prueba de Hipótesis para dos colas, nosotros dividimos el
valor p entre dos para obtener el valor para una sola cola.
Primer paso. Introducimos los datos en una columna, asignándole nombre a la variable,
en este caso le llamaremos truchas.
Segundo paso. Nos vamos al menú y seleccionamos Statistics
One Sample Test
Compare Means
57
Prueba de Hipótesis para la media de una población
Ing. Hernán Trujillo Avila
Tercer paso. Aparece el siguiente recuadro, donde habremos de dar de alta en el
recuadro Test Variable(s), nuestra variable a analizar, en este caso “truchas”.En el
pequeño recuadro Test Value, debemos dar el valor de la hipótesis a probar, en este
caso: 4.Damos OK.
En Options tendremos que dar
95% nivel de confianza.
Aparecen los siguientes resultados:
“El valor p aparece en la columna
Sig(2-tails),donde el valor de P
exacto es 0.531 , para una sola
cola sería 0.2655 >  , por lo
tanto la Hipótesis nula se
Acepta.”
58
Prueba de Hipótesis para la media de una población
Ing. Hernán Trujillo Avila
Ejercicio 2.1.
2.1. Las especificaciones de construcción en cierta ciudad requieren que las tuberías
de desagüe empleadas en áreas residenciales tengan una resistencia media a la
ruptura de más de 2500 libras por pie lineal. Un fabricante que quisiera proveer a la
ciudad de tubos para desagüe ha presentado una licitación junto con la siguiente
información adicional: un contratista independiente seleccionó al azar siete secciones
de los tubos del fabricante y determinó su resistencia a la ruptura. Los resultados
(libras por pie lineal) son los siguientes:
2610
2750
2420
2510
2540
2490
2680
¿ hay suficientes pruebas para llegar a la conclusión de que los tubos para desagüe del
fabricante cumplen con las especificaciones requeridas?. Utilice un nivel de
significancia de  = 0.10
Pruebe los resultados en SPSS o en algún otro Software.
2.2. Se investigó el efecto de las descomposturas de máquinas sobre el rendimiento
de un sistema de fabricación empleando simulación por computadora (Industrial
Engineering, Agosto,1990). El estudio de simulación se concentró en un solo sistema de
máquina herramienta con varias características; incluido un tiempo medio entre
llegadas de 1.25 minutos, un tiempo de procesamiento constante de un minuto y una
tasa de descompostura de la máquina de 10% del tiempo. Después de n= 5 series de
simulación con duración de 160 horas, la producción media por semana de40 horas
fue X =1908.8 piezas. En el caso de un sistema sin descomposturas, la producción
media es de 1920 piezas. Suponiendo que la desviación estándar de las cinco series de
muestra fue s= 18 piezas por semana de 40 horas, pruebe la hipótesis de que la
verdadera producción media por semana de 40 horas para el sistema, es menor que
1920 piezas, utilice  = 0.05
59
Prueba de Hipótesis para la media de una población
Ing. Hernán Trujillo Avila
TAREA 2.1
2.1. Los resultados del segundo estudio nacional para examen de la nutrición y salud
de de Estados Unidos indican que la concentración media de plomo en la sangre de
individuos con edades de entre 6 meses y 74 años es de 14 µg/dl (Anlytical
Chemestry, Febrero de 1986). Sin embargo se observó que la concentración media de
plomo en la sangre de niños de raza negra de menos de 5 años de edad es
significativamente más alta que esta cifra. Suponga que en una muestra aleatoria de
200 niños negros de menos de 5 años de edad la concentración media de plomo en la
sangre es de 21 µg/dl y la desviación estándar es de 10 µg/dl. ¿Hay pruebas
suficientes para indicar que la verdadera concentración media de plomo en la sangre
de niños negros pequeños es mayor que 14 µg/dl?. Pruebe con =0.01
R. Sí. z=9.9
2.2. En Enviromental Science & Technology ( Octubre de 1993) se informó de un
estudio de suelos contaminados en los países bajos. Se investigó un total de 72
especimenes de tierra de 400 gr, los cuales se secaron y analizaron para medir el nivel
de contaminante cianuro (miligramos por kilogramo de tierra) en cada espécimen de
suelo empleando un método de microscopía de infrarrojo. La muestra arrojó un nivel
medio de cianuro de 84 mg/kg y una desviación estándar de 80 mg/kg. Utilice esta
información para probar la hipótesis de que el verdadero nivel medio de cianuro en los
suelos de los países bajos es menor que 100 mg/kg. Pruebe con = 0.10
R. z= -1.7,rechazar H0
60
Prueba de Hipótesis para la media de una población
Ing. Hernán Trujillo Avila
61