TRABAJO

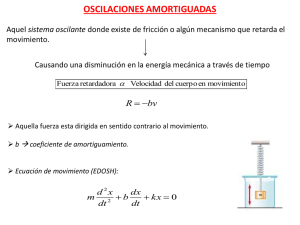
TRABAJO
El trabajo hecho en un sistema mecánico, es el producto de la fuerza multiplicado por la
distancia (el torque multiplicado por el desplazamiento angular) a través del cual es ejecutado,
ambos fuerza y distancia, son medidos en la misma dirección. Por ejemplo, si un cuerpo es
empujado con una fuerza horizontal “F” en Newtons una distancia “x” en metros, el trabajo hecho
“W” es:
W=Fx
[N - m]
Para un resorte translacional (lineal) con una constante “k”, el trabajo hecho para un
desplazamiento infinitesimal “dx” esta dado por:
W = F x = kx dx
El trabajo total hecho sobre cualquier desplazamiento es la integral del trabajo hecho por un
desplazamiento infinitesimal “dx”. Si el desplazamiento total es “x” entonces:
x
x
x2
WT   kxdx  k  xdx  k
2
0
0
x

WT 
0
1 2
kx
2
Para resortes torsionales tenemos:

WT   kd

WT 
0
1 2
k
2
Donde  es el desplazamiento angular.
ENERGÍA
En forma general, la energía puede ser definida como la capacidad o habilidad para hacer
un trabajo, se encuentra en diferentes formas, pudiéndose convertir de una a otra. Un sistema se
dice que posee energía. Cuando un sistema hace un trabajo mecánico, la energía del sistema decrece
una cantidad igual a la energía requerida para hacer el trabajo; las unidades son las mismas que las
de trabajo.
ENERGÍA POTENCIAL
En un sistema mecánico, únicamente la masa y el resorte pueden almacenar energía
potencial. El cambio de la energía potencial almacenada en un sistema es igual al trabajo requerido
para cambiar la configuración del sistema.
Para un cuerpo de masa “m” en un campo gravitacional, la energía potencial “EP” medido
con algún nivel de referencia, es “mg” veces la altura “h” ó:
h
E P   mgdx  mgx 0
h
0

E P  mgh
Notemos que si el cuerpo se deja caer, tiene la capacidad de trabajar, ya que el peso “mg”
(fuerza) viajara una distancia “h” cuando es liberado, cuando esto sucede, “EP” disminuye y se
traduce en “EC”.
Para un resorte translacional (lineal), la “EP” es igual al trabajo neto hecho por las fuerzas
que actúan sobre los extremos (del resorte) cuando es comprimido o alargado como F = kx.
Donde “x” es el desplazamiento neto de los extremos del resorte, entonces.
x
x
0
0
E P   Fdx   kxdx 
1 2
kx
2
Si los valores inicial y final de “x” son x1 y x2 el cambio en “EP” es:
x2
x2
x1
x1
E P   Fdx   kxdx 
1 2 1 2
kx 2  kx 1
2
2
Notemos que la EP almacenada en el resorte, no depende de si el resorte es comprimido o
alargado.
Similarmente, el cambio de EP en un resorte torsional:
2
2
1
1
E P   Fd   k t d 
1
1
k t  22  k t 12
2
2
ENERGÍA CINETICA
Unicamente los elementos de inercia pueden almacenar energía cinética en los sistemas
mecánicos, por ejemplo una masa “m” en una translación a una velocidad “v” tiene energía cinética
“EC = ½ mv2”, mientras que el momento de inercia “J” en una rotación a una velocidad angular “  ”
tiene por ecuación “EC = ½ J  2.
Un cambio en la energía cinética de una masa “m” es igual al trabajo hecho en la masa por
la aplicación de una fuerza ya sea para acelerar o para desacelerar. Así el cambio para una masa
“m” de la energía cinética y que se mueve en la línea recta es:
x2
t2
x1
t1
E C   Fdx   F
t
2
dx
dt   Fvdt 
dt
t1
t2
v2
t1
v1
E C   mv vdv   mvdv 
E C 
1
1
mv22  mv12
2
2
Un cambio en la EC de un momento de inercia en una rotación hará una velocidad angular
 es:
E C 
1 2 1 2
J 2  J1
2
2
Donde J es el momento de inercia y  la velocidad angular.
POTENCIA Y ENERGÍA
Es el rango de tiempo en hacer un trabajo, esto es:
Potencia P 
dW
dt
Donde “dW” detona el trabajo hecho durante un intervalo de tiempo “dt”. La potencia
promedio durante “t2 – t1” segundos, puede determinarse por medio del trabajo hecho en “t2 – t1”
segundos ó.
P
T rabajohechoen (t 2  t 1 ) seg
(t 2  t 1 ) seg
La potencia requerida en comprimir un resorte ó alargarlo es:
P
dW Fdx

 Fx  kxx
dt
dt
Como la energía potencial de un resorte comprimido ó alargado una cantidad “x” es “EP = ½
kx ”, obtenemos:
2

P  kxx  E
P
La potencia requerida para acelerar una masa en una línea recta es:
P
dW Fdx

 Fx  mxx
dt
dt
Como la energía cinética de una masa “m” moviéndose a una velocidad “v” es “E C = ½
mv2” entonces:
P  mxx  mv v  E C
Así para una masa “m” moviéndose en una línea recta, la potencia “P” es el rango de
cambio de energía cinética EC.
Considerando ahora un sistema conservativo, en el que la energía esta en la forma de
cinética y/o potencial, como la energía que entra y sale de un sistema conservativo en forma de
trabajo, obtenemos lo siguiente:
(EP + EC) = W
Donde (EP + EC) es el cambio en la energía total y “W” es el trabajo neto hecho en el
sistema por una fuerza externa. Si no hay energía externa que entre al sistema, entonces:
(EP + EC) = 0
Lo que resulta en:
EP + EC = constante
Refiriéndonos a la siguiente figura, y suponiendo que no hay fricción, entonces el sistema
puede ser considerado como conservativo, la energía cinética y potencial están dadas por:
Consecuentemente, en la ausencia de cualquier energía externa de entrada:
EP  EC 
1 2 1 2
kx  mx  constante
2
2
La ecuación de movimiento de este sistema puede ser obtenida por diferenciación de la
energía total como respecto a “t”, haciendo el resultado igual a cero:
d
E P  E C   kxx  mx x  mx  kx x  0
dt
Como " x " no siempre es cero, tenemos:
mx  kx  0
Que es la ecuación de movimiento del sistema, que ha sido determinada con anterioridad.
SISTEMAS CON UN GRADO DE LIBERTAD CON AMORTIGUAMIENTO
El proceso por el cual la vibración disminuye continuamente en amplitud, recibe el nombre
de amortiguación, la energía del sistema de vibración se disipa como fricción o calor, se transmite
en forma de sonido. En el mecanismo de la amortiguación ésta puede tomar cualquiera de varias
formas, y con frecuencia puede encontrarse presente al mismo tiempo más de una de ellas.
La amortiguación fluida puede ser viscosa o turbulenta. En la amortiguación viscosa, la
fuerza de amortiguación es proporcional a la velocidad. En la amortiguación turbulenta, la fuerza es
proporcional al cuadrado de la velocidad. En la fricción seca o amortiguación de Coulomb, la fuerza
de amortiguación es constante. Esta se causa por la fricción cinética entre superficies deslizantes
secas. La amortiguación sólida o amortiguación histerésica se ocasiona por la fricción interna o
histerésis, cuando se deforma un cuerpo sólido. La amplitud bajo esfuerzo es una medida de la
amortiguación sólida.
El mecanismo de amortiguación más comúnmente usado es de la amortiguación viscosa, en
el cual la fuerza de amortiguación es proporcional a la velocidad. Estrictamente hablando, esto sólo
es válido para una amortiguación como la causada por el flujo laminar de un fluido viscoso a través
de una ranura; por ejemplo, en un absorbechoques o amortiguador, alrededor de un émbolo
dispuesto en un cilindro, o en la oscilación de un muñón de flecha dentro de un cojinete. En cada
uno de estos casos, la constante de proporcionalidad depende de la viscosidad absoluta del fluido, el
área superficial, y el espesor de la película del fluido. Todos estos factores se pueden hacer
constantes para un conjunto dado de condiciones físicas. Estas normas son casi los únicos ejemplos
prácticos de amortiguación viscosa. No obstante, otras formas de amortiguación se aproximan a la
amortiguación viscosa, si las fuerzas de disipación son pequeñas. Lord Rayleigh hizo esta
aproximación cuando utilizó la amortiguación viscosa para aproximar los efectos combinados de la
amortiguación viscosa tiene la ventaja de linealizar la ecuación de movimiento. Si las fuerzas
disipativas no son pequeñas, se puede introducir un error considerable al suponer que la
amortiguación es viscosa cuando ésta no lo es.
Para iniciar nuestro estudio de este tipo de sistemas haremos uso de lo que ya hemos
estudiado, i.e. volveremos hacer uso del sistema MASA-RESORTE que tiene todas las
características significativas de un problema de vibración.
Consideremos una masa “m” que tiene 1 GL, esto es como ya vimos, su localización en
cualquier tiempo esta especificando por una coordenada “x”. La masa “m” esta contenida por un
resorte y una fuerza externa. “F(t) w y A magnitud varia con el tiempo y esta aplicada a la masa
según se muestra a continuación.
El diagrama de cuerpo libre se muestra cuando tiene una velocidad positiva y un
desplazamiento medido desde la posición de equilibrio estático ( x = 0) el hecho de que la fuerza de
fricción se opone al movimiento de la masa es indicado por la fuerza “Fr”, que es usualmente una
función de la velocidad del sistema y depende de la naturaleza de las fuerzas en contacto y de las
condiciones de la lubricación.
Las fuerzas que actúan sobre la masa son en general de 3 clases, a saber:
i)
ii)
iii)
Existe una fuerza excitadora que es externamente aplicada y que causa el
movimiento del sistema (cuya magnitud varia con el tiempo) F(t).
Existe una fuerza restablecedora “FR”, fuerza ejercida por el resorte sobre la masa y
tiende a restablecerla a su posición original (i.e. su dirección es siempre hacia la
posición de equilibrio del sistema).
Existe una fuerza amortiguadora “Fr” que siempre se opone al movimiento del
sistema y que es responsable de la disipación de energía (en muchos casos la fuerza
amortiguadora es proporcional a la velocidad).
De lo anterior, la ecuación de movimiento del sistema puede escribirse como: sabemos que.
F = ma y para el sistema de fuerzas
mx   Fi  F(t)  FR  Fr

F  mx
i

mx  F(t)  FR  Fr
Estas tres fuerzas junto con la ecuación de movimiento, caracterizan el problema de
vibración.
FUERZAS DE EXCITACIÓN
Las fuerzas excitadoras aparecen en diferentes formas pueden por ejemplo ser transitorias
como las causadas por el impacto de algún cuerpo externo ó pueden ser repetitivas, causadas por
una seria de impactos. Algunas partes reciprocantes o rotativas de maquinas con frecuencia
producen fuerzas alternativas desequilibradas, que tienen una variación sinusoidal. Consideramos
por ejemplo, la rotación de un disco desbalanceado, como se muestra en la figura.
Este arreglo representa una vibración típica aislada, para una maquina rotativa que esta
montada. El disco de masa “m” rota alrededor del centro o con una velocidad “w”. El centro de
masa del disco esta localizado a una distancia “r” del centro de rotación.
El sistema esta montado sobre una gran masa M que puede moverse únicamente en
dirección vertical M esta soportada por un resorte que tiene una constante “k” y un amortiguador
“c” conectados a M por soportes fijos. Si suponemos que el movimiento de M es pequeño
comparando con “r”, entonces el movimiento de “m” puede tomarse como circular y la aceleración
del centro de masa del disco es “r2”. Existe así una fuerza (F = ma) de magnitud “mr2” actuando
en una dirección radial sobre la gran masa M. La componente de la fuerza en la dirección “Y” , esto
es la componente de la fuerza que provoca el movimiento del sistema es “mr 2 2 sen 0”.
Supongamos que el disco rota con una velocidad constante, tenemos para la fuerza excitadora:
F(t) = mr2 sen t
SISTEMA MASA-RESORTE AMORTIGUADO
Muchos sistemas involucran algún tipo de amortiguamiento, ya sea amortiguamiento
viscoso, seco, magnético, etc. Tal amortiguamiento no solo disminuye el movimiento, también
provoca que el movimiento pare eventualmente. El diagrama muestra un sistema masa - resorte
amortiguador. Suponga que la masa es jalada hacia abajo y luego se libera.
i)
ii)
iii)
Si el amortiguador es ligero, ocurrida el movimiento vibratorio (se dice sistema
subamortiguado).
Si el amortiguamiento es grande, el movimiento vibratorio no ocurra (el sistema se
dice sobreamortiguado)
Un sistema críticamente amortiguado, es uno en el cual, el grado de
amortiguamiento es tal, que el movimiento resultante esta en la frontera entre los
casos subamortiguado y sobreamortiguado.
En el dibujo anterior tres fuerzas actúan sobre la masa; la fuerza del resorte la fuerza
amortiguadora y la fuerza gravitacional. Notamos que si medimos el desplazamiento de la masa
desde una posición de equilibrio estático (así la fuerza gravitacional esta balanceada por la
deflexión de equilibrio estático del resorte), la fuerza gravitacional no entrara en la ecuación de
movimiento.
Así midiendo el desplazamiento x, desde la posición de equilibrio estático, obtenemos la
ecuación de movimiento:
mx  fuerzas  kx  bx ó mx  bx  kx  0
Esta ecuación describe el movimiento del sistema y es también el modelo matemático. Las
soluciones de este tipo de ecuaciones pueden escribirse en forma de exponenciales e rt, donde “r”
satisface la ecuación característica (auxiliar).
mr2 + br + k = 0
cuyas raíces son:
r
 b  b 2  4mk
2m
Habrá que analizar los casos posibles del discriminante: b2  4mk pues cada uno representa
una forma diferente de la solución general, veamos como:
i)
ii)
iii)
b2 < 4mk Esto significa que las raíces son complejas (conjugadas) entonces el
coeficiente de fricción es pequeño y la fuerza amortiguadora no es particularmente
grande.
b2 = 4mk Esto significa que las raíces son reales e iguales y tiene un significado
particularmente interesante, que veremos más adelante.
b2 > 4mk Esto significa que las raíces son reales y distintas entonces el coeficiente
de fricción es grande y la fuerza amortiguadora también lo es.
NOTA: La más importante característica de las fuerzas amortiguadoras es que su dirección
siempre se opone a la dirección de movimiento el trabajo hecho por una fuerza amortiguadora es así
siempre negativo y la energía es disipada del sistema así que:
Fr  bx
Veamos cada caso de manera particular:
CASO b2 < 4mk.
Si el discriminante b2  4mk, se cumple que b2 < 4mk tendremos lo siguiente:
r1,2
 b  b 2  4mk  b 


2m
r1,2  
 14mk  b 2 
2m

b
 1
4mk  b 2
2m

b
4mk  b 2
b
4mk  b 2
b
k
b2
i

i



i

2m
2m
2m
2m
m 4m 2
4m 2
k
b2

 r se puede expresarcomo:
m 4m 2
b

r1  
 i

b

2m

i  
2m
r   b  i 
 2
2m
Si hacemos  
r1,2
Como hemos visto la solución a la ecuación mx  bx  kx  0 es una combinación lineal
de la siguiente forma:
x  ae r¹ t + be r² t
Luego al sustituir se tiene:
x  ae

 b
 
i   t 
 
 
 2 m
x e
bt

2m
 be
ae
i t
 b
 
i   t 
 
 
 2 m
 be i t


Conviene recordar que una combinación lineal arbitraria de e i t y e -i t (i.e. a e i t + b e -i t)
es equivalente a una combinación lineal arbitraria de cos t y sen t, luego la expresión anterior es
equivalente a:
xe

bt
2m
a cost  b sen t 
La expresión entre paréntesis es ya conocida y sabemos que se puede reescribir como:

x  Ae
bt
2m
sent  0 
Que es la solución para este caso (b2 < 4mk).
Donde Ae

bt
2m
es la amplitud de oscilación y 0 es la fase inicial.
Supongamos por un momento que tenemos fricción lo suficiente que pueda considerarse
pequeña, en cuyo caso se puede hablar de una frecuencia circular aproximada a:

k
b2

m 4m 2
Ahora bien si b  0, y ello significa en términos físicos que nuestro sistema carece de
amortiguador o es nulo. Entonces la expresión anterior será:

k
b2
k
k


0 
2
m 4m
m
m


k
m
Una forma de observar el efecto amortiguador en el sistema es a través del comportamiento
de la amplitud en un período, esto es:
2
k
b2
pero  


m 4m 2
2
2
T

k
b2
k
b2 



1

m 4m 2
m  4mk 
Sabemos que : T 
Luego
b2
 0 (tiendea cero),entonces:
4mk
2
T
k
m
Hemossupuesto que b 2  4mk 
Con este período podemos estudiar el comportamiento de la amplitud después de un
período:
Como
Ae
bt

2m
 Ae

b  2  
2 m  k m 
 Ae
2 b

2m k m
 Ae


b
2  

 2 m k m 
 Ae


b

2  
 4 m2 k m 


1
 Ae
 b2  2
2  

 4 mk 
Recordemos que e-x  1 si x es pequeña, se sigue entonces que si b2 << 4mk, el
exponencial no presenta una caída grande en un período y se dice que el amortiguamiento es
despreciable.
CASO b2  4mk.
Desde un punto de vista físico, la condición b2  4mk, significa que las cantidades b, m y k
que normalmente son medidas experimentalmente, deben necesariamente ser tales que se cumpla
dicha condición (b2  4mk) pero como no existe posibilidad para que esto ocurra, entonces
cualquier desviación en la igualdad resultará en cualquiera de los otros casos que se están
analizando.
Aquí la solución a la ecuación mx  bx  kx  0 es de la forma x  e

bt
2m
At  B
con
A,B constantes por determinar.
CASO b2 > 4mk.
Cuando tenemos un sistema masa - resorte - amortiguador con la característica de que la
fricción o mejor dicho la amortiguación es lo suficientemente grande (no habrá movimiento de
vibración) esto es si satisface la condición b2 > 4mk, la solución bajo este criterio de la ecuación
diferencial, adquiere la forma:
x  C1e r¹ t + C2e r² t
Con
r1 
 b  b 2  4mk
2m
y
r2 
 b  b 2  4mk
2m
El análisis hecho en los tres casos anteriores, puede llevarse acabo con el siguiente método:
Definimos la siguiente cantidad adimensional:

b
CC
Donde  es llamado factor (relación) de amortiguamiento.
CC es conocido como coeficiente de amortiguamiento crítico y esta definido como:
C C  2m  2 km;
con  
k
m
Ahora bien, las raíces de la ecuación característica: mr2 + br + k  0 pueden expresarse
como una función de  así:

Sabemos que :
b
CC

b  C C  2m  b  2 m
Por otro lado:
r1,2  
b
b 2  4mk
2 m
1



4 2  2 m 2  4mk 
2m
2m
2m
2m
r1,2   
4 2  2 m 2  4mk
k
    2  2      2  2   2 
2
m
4m
r1,2      2  1
En esta última expresión, no detendremos a analizar de nueva cuenta el discriminante de la
raíz y podemos observar los siguientes casos:
i)
ii)
iii)
Sí 2 > 1  r1  r2; r1, r2  R y se tiene que b > CC en este caso se dice que el
sistema esta sobreamortiguado.
Sí 2  1  r1  r2; r1, r2  R y b  CC caso críticamente amortiguado.
Sí 2 < 1  r1  r2 ; r1 , r2  C y b  CC se trata de un sistema subamortiguado.
DECREMENTO LOGARITMICO
Recordemos que en el caso de un sistema subamortiguado, la amplitud de oscilación esta
dad por:
x  Ae

bt
2m
Al observar la figura, podemos establecer lo siguiente:
La amplitud es máxima en el tiempo t  t0 y tiene un valor x0, un ciclo después dicha
amplitud ha disminuido a un valor x1 en un tiempo t  t0 + Td; dos ciclos después, la amplitud ha
disminuido a x2 en un tiempo t  t0 + 2Td, y así sucesivamente hasta que el sistema pare.
Hemos visto la constante A depende en magnitud del valor de x0 en t  t0. Ahora bien para
un sistema amortiguado como el aquí analizado la expresión para el período es:
2
Td 
Podemos definir a x 0  Ae

bt O
2m
k
b2

m 4m 2
y tendremos la siguiente sucesión de eventos:
x 0  Ae

bt O
2m
Un ciclo después:
x1  Ae

b
 t 0 Td 
2m
 Ae

bt 0
2m
e

bTd
2m
 x 0e

bTd
2m
Dos ciclos después:
x 2  Ae

b
 t 0  2 Td 
2m
 x 0e


b
 2 Td 
2m

En el enésimo ciclo:
x n  Ae
 b

b
 t 0  nTd 
2m
 x 0e

b
nTd 
2m
 xn  x 0 e

b
nTd 
2m

En donde 
Td  se le llama decremento logarítmico y se define como:
 2m


b
Td
2m
Y se debe entender como una medida de amortiguación del sistema y es una cantidad
adimensional.
Ahoracomo: xn  x 0 e
Luego :
ln

b
 nTd 
2m
 xn  x 0 e  n 
xn
 e  n
x0
xn
1 x
 n y entonces   ln 0
x0
n xn
Esta última ecuación nos establece una relación entre las amplitudes x0 y xn.
Debido a que se ha definido un nuevo período "amortiguado" que se expresa mediante:
Td 
2
k
b2

m 4m 2
Entonces podemos decir y hablar de la existencia de una frecuencia amortiguada d,
definida como:
d 
k
b2

m 4m 2
Se sabe que  
k
, estas dos expresiones de la frecuencia, se relaciona por medio del
m
número  de la siguiente forma:
d   1   2 con  
b
b

C C 2 km
Entonces como:

b
b  2 
Td 
  
2m
2m   d 
Usando lo anterior:


b 
2


2m   n 1   2 
Recordemos que:
C C  2mn   
 b 
2



1    2mn 
1  2
Por último:

Y de esta expresión:

2
2
2
1 2

22   2
DESBALANCE
ROTATORIO
El desbalance en máquinas rotatorias es una fuente común de excitación vibratoria.
En muchos sistemas mecánicos rotativos, las flechas y discos no son perfectamente uniformes, esto
frecuentemente provoca fuerzas desbalanceadas que son causa de excesivas vibraciones y pueden
fallar los componentes del sistema.
El desbalanceo rotativo ocurre en sistemas como rotores, rines, ventiladores, etc.
Consideramos aquí una máquina (sistema Resorte – Masa) de un grado de libertad amortiguada con
coeficientes k y b restringido a moverse en la dirección vertical y excitado por una máquina
rotatoria no balanceada, como se muestra en la siguiente figura.
La masa total de la máquina es M. La máquina tiene un rotor montado sobre un balero cuyo centro
es “O”, el rotor gira en sentido antiorario con una velocidad angular de
F
en r/s.
La masa tiene una distribución no uniforme en el rotor; esto resulta en un rotor desbalanceado
equivalente a una masa “m” excéntrica, localizada a una distancia “e” del centro del rotor.
La vibración de la máquina se supone es únicamente en dirección vertical.
Se puede demostrar del análisis de equilibrio estático que el peso de la máquina se anula con la
deflexión estática del resorte.
m
e
wt
X
M
K/2
KX
CX
KX
KX
CX
KX
K/2
C
FUERZA PERTURBADOA ARMONICA QUE RESULTA DE UN DESBALANCE
Se puede deducir entonces de la siguiente manera:
El desbalance está representado por una masa excéntrica “m” con excentricidad “e” que rota con
una velocidad angular “F”. Si “x” representa el desplazamiento de la masa no rotante (M – m),
desde la posición de equilibrio, el desplazamiento de m es:
xm = x + e sen f t
Y su aceleración es expresada en erminos de x m es por tanto :
x m = x - 2f e sen f t
Si M es la masa total de la máquina incluyendo la masa excéntrica, la masa de la máquina que tiene
una aceleración x es(M – m) , por lo tanto las fuerzas totales de inercia serán:
oo
oo
FUERZA DE INERCIA = (M – m) x  m x m
De acuerdo con la segunda ley de Newton; estas deben ser iguales a las fuerzas aplicadas, esto es:
( M - m ) x + m x m = -b x - k x
Usando el valor de x m y reagrupando tenemos que:
M x + b x + kx = m e 2f t
En el segundo miembro de esta ultima ecuación, podemos establecer que: Fo = m k 2f
Donde tambien es claro que Fo depende de la frecuencia del rotor.
Ahora, por la propia constitución del sistema , la frecuencia natural del mismo es:
k
=
m
Y la solución en estado estable es:
Xo
xp(t) =
( 1 - r2 ) + ( 2r  )2
Donde
 , es el ángulo
de fase que se definió como:
sen ( f t -  )
2r 
 = Tan
-1
1 – r2
Y la constante xo en este caso es:
me2f
Fo
Xo =
=
k
me2f
=
m
=
2 M
k
e
r2
M
Luego Xp (t), toma la forma:
me
r2
M
sen ( f t -  )
xp ( t ) =
( 1 - r2 ) + ( 2r  )2
En la que simplificando queda:
me
r sen ( f t -  )
xp ( t ) =
M
r2
Donde :
r =
( 1- r2 )2 + ( 2r  )2
Donde r, es el factor de Magnificación.
Si se analiza la ecuación del desplazamiento xp ( t ) se puede observar que para estado estable es
proporcional tanto a la masa m como a la exentricidad e.
TRANSMISION DE FUERZA
En estado estable, la fuerza transmitida a los soportes, en el caso de desbalanceo rotativo es:
Ft = k xp + b x p
Donde x p se obtiene diferenciando xp .
x p= f ( m e / m ) r cos ( f t -  )
Luego Ft usando xp queda:
Ft = ( m e / m ) r [ k sen ( f t -  ) + b f cos ( f t -  )
Que puede escribirse como:
me
r
F1 =
k2 + ( C f )2
sen ( f t -  )
M
Donde:
=-t
y el ángulo de fase
t
esta definido como:
b f
 t = Tan –1
= Tan –1 ( 2r  )
k
me
k r
luego: F1 =
1 + ( 2r  )2
sen ( f t -  )
M
Como: k / M = 2n
Lo que permite expresar a:
F1 = ( m e 2n ) t sen ( f t -  )
Donde: t esta definida como:
r2
t = r
1 + ( 2r  )2
1 + ( 2r  )2 =
( 1 – r 2 ) 2 + ( 2r  )2
BALANCE DE ROTORES
NOTA: En términos generales se distinguen dos tipos de desbalance rotatorio, a saber:
 DESBALANCE ESTÁTICO.
Cuando las masas no balanceadas yacen en un plano singular, como en el caso de un rotor de disco
delgado, el desbalance resultante es una fuerza radial. Como se muestra en la figura, tal desbalance
puede detectarse por medio de una prueba estática en la cual el conjunto eje-rueda es colocado
sobre un par de rieles horizontales. La rueda rodará hasta una posición en donde el punto pesado
estará directamente debajo del eje.
Como tal desbalance puede detectarse sin necesidad de hacer girar la rueda, se le llama desbalance
estático.
 DESBALANCEO DINÁMICO.
Cuando el desbalance aparece en más de un plano, la resultante es una fuerza y un momento de
balanceo que constituyen el llamado desbalance dinámico. Como se describió previamente, una
prueba estática puede detectar la fuerza resultante pero el momento de balanceo no puede detectarse
sin hacer girar el rotor. Por ejemplo, consideremos un eje con discos como en el caso de la
siguiente figura.
Si las dos masas no balanceadas son iguales y están a 180°, el rotor estará estáticamente balanceado
con respecto al eje del árbol. Sin embargo, cuando el rotor está girando, cada disco no balanceado
establecerá una fuerza centrífuga rotante que tiende a mecer el árbol en sus cojinetes.
Fig. Sistema Con Desbalance Dinámico.
En general, un rotor largo tal como una armadura de motor o el cigüeñal de u motor de automóvil,
puede considerarse como una serie de discos delgados, cada uno, con algún desbalance. Tales
rotores deben ser ensayados rotando para poder detectar el desbalance.
Las máquinas que detectan y corrigen el desbalance del rotor, se denominan Máquinas de balanceo.
Esencialmente la máquina de balanceo consta de cojinetes portantes montados sobre resortes a fin
de detectar las fuerzas no balanceadas por su movimiento.
Conociendo la amplitud de cada cojinete y su fase relativa, es posible determinar el desbalance y
corregirlo.