Repasocinedin

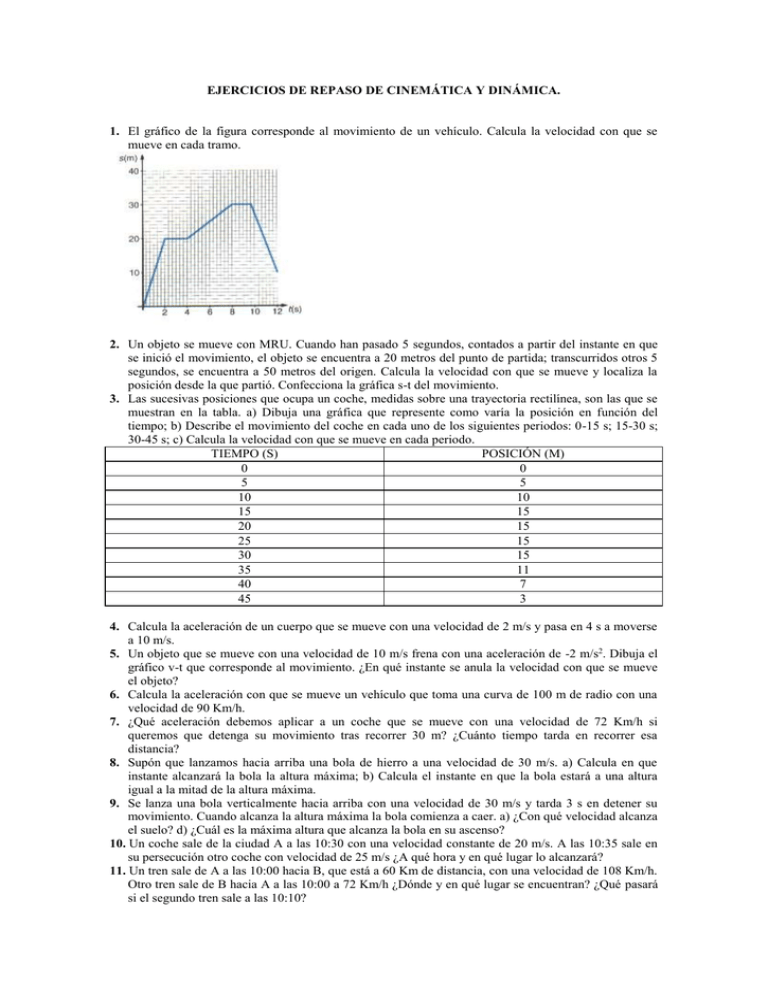
EJERCICIOS DE REPASO DE CINEMÁTICA Y DINÁMICA.
1. El gráfico de la figura corresponde al movimiento de un vehículo. Calcula la velocidad con que se
mueve en cada tramo.
2. Un objeto se mueve con MRU. Cuando han pasado 5 segundos, contados a partir del instante en que
se inició el movimiento, el objeto se encuentra a 20 metros del punto de partida; transcurridos otros 5
segundos, se encuentra a 50 metros del origen. Calcula la velocidad con que se mueve y localiza la
posición desde la que partió. Confecciona la gráfica s-t del movimiento.
3. Las sucesivas posiciones que ocupa un coche, medidas sobre una trayectoria rectilínea, son las que se
muestran en la tabla. a) Dibuja una gráfica que represente como varía la posición en función del
tiempo; b) Describe el movimiento del coche en cada uno de los siguientes periodos: 0-15 s; 15-30 s;
30-45 s; c) Calcula la velocidad con que se mueve en cada periodo.
TIEMPO (S)
POSICIÓN (M)
0
0
5
5
10
10
15
15
20
15
25
15
30
15
35
11
40
7
45
3
4. Calcula la aceleración de un cuerpo que se mueve con una velocidad de 2 m/s y pasa en 4 s a moverse
a 10 m/s.
5. Un objeto que se mueve con una velocidad de 10 m/s frena con una aceleración de -2 m/s2. Dibuja el
gráfico v-t que corresponde al movimiento. ¿En qué instante se anula la velocidad con que se mueve
el objeto?
6. Calcula la aceleración con que se mueve un vehículo que toma una curva de 100 m de radio con una
velocidad de 90 Km/h.
7. ¿Qué aceleración debemos aplicar a un coche que se mueve con una velocidad de 72 Km/h si
queremos que detenga su movimiento tras recorrer 30 m? ¿Cuánto tiempo tarda en recorrer esa
distancia?
8. Supón que lanzamos hacia arriba una bola de hierro a una velocidad de 30 m/s. a) Calcula en que
instante alcanzará la bola la altura máxima; b) Calcula el instante en que la bola estará a una altura
igual a la mitad de la altura máxima.
9. Se lanza una bola verticalmente hacia arriba con una velocidad de 30 m/s y tarda 3 s en detener su
movimiento. Cuando alcanza la altura máxima la bola comienza a caer. a) ¿Con qué velocidad alcanza
el suelo? d) ¿Cuál es la máxima altura que alcanza la bola en su ascenso?
10. Un coche sale de la ciudad A a las 10:30 con una velocidad constante de 20 m/s. A las 10:35 sale en
su persecución otro coche con velocidad de 25 m/s ¿A qué hora y en qué lugar lo alcanzará?
11. Un tren sale de A a las 10:00 hacia B, que está a 60 Km de distancia, con una velocidad de 108 Km/h.
Otro tren sale de B hacia A a las 10:00 a 72 Km/h ¿Dónde y en qué lugar se encuentran? ¿Qué pasará
si el segundo tren sale a las 10:10?
12. Calcula el periodo de una rueda que gira 8 veces por segundo.
13. Calcula el periodo de rotación de la Tierra.
14. Calcula el espacio angular recorrido por dos ruedas de 20 y 50 cm de radio si ambas recorren 40
metros. ¿Cuál tiene que dar más vueltas? ¿Cuántas vueltas da cada rueda?
15. Si quiero llegar a Madrid, distante de mi origen 416 Km, antes de las 10 horas de la mañana y la
velocidad media que podré mantener por la autopista es de 120 Km/h, ¿a qué hora debo partir de mi
origen?
16. Un móvil parte del reposo con aceleración constante de 2 m/s 2 con MRUA. Determinar: la velocidad
que tiene al cabo de 20 segundos, el espacio recorrido en esos 20 s, la velocidad media en estos 20 s.
¿Qué tiempo tarda en alcanzar una velocidad de 90 m/s?
17. ¿Con qué velocidad hay que lanzar una pelota verticalmente y hacia arriba para que llegue hasta una
altura de 15 m? ¿Qué tiempo estará subiendo?
18. Desde lo alto de una torre se deja caer una pelota desde el reposo. Tarda en llegar al suelo 3’5 s.
Calcular: la altura de la torre, la velocidad con que llega la pelota al suelo y la velocidad media que ha
llevado la pelota.
19. Dos móviles parten de un mismo punto en la misma dirección y sentido con v 0=0. El primero con
aceleración de 2 m/s2 y el segundo con aceleración de 1’5 m/s2 ¿Qué distancia les separa al cabo de un
minuto de haberse puesto en movimiento?
20. La ecuación de un movimiento es v=30-4t (m/s). Determina su aceleración y su velocidad en t=2 s.
21. La ecuación de un movimiento es s=100+10t-t2. ¿Cuánto tardará el móvil en parase? ¿Qué distancia
recorre hasta que se para? ¿Cuál es su posición en ese instante respecto al origen? Determinar la
velocidad 2 s antes de pararse.
22. Una rueda de 25 cm de diámetro gira con una velocidad de 130 rpm. Calcular: la velocidad angular, el
periodo, la frecuencia, velocidad de un punto de la periferia y la aceleración centrípeta.
23. Una polea de 5 dm de radio gira con una velocidad en la periferia de 15 m/s. Hallar el número de
vueltas que da por minuto, su velocidad angular y el espacio angular (radianes) recorrido en 2
minutos.
24. Calcula la aceleración y deceleración de un móvil cuya velocidad varía con el tiempo según la gráfica
siguiente:
25.Un disco de 10 cm de radio gira con una velocidad de 120 rpm. Calcular: a)velocidad angular; b)
periodo; c) velocidad lineal en un punto de la periferia; d) aceleración centrípeta en la periferia; e)
espacio recorrido por un punto que dista 2 cm del centro, en 3 minutos; f) ángulo barrido por un punto de
la periferia en 1’5 m.
26.A un cuerpo de 10 Kg de masa se le aplica una fuerza constante de 117’6 N. Calcula la aceleración
que le comunica.
27.En la siguiente situación calcula la tensión de la cuerda y la aceleración con la que se mueve el
sistema.
M1=2Kg
M2=10 Kg
28.Un cuerpo de 1’5 Kg de masa se desliza sobre una superficie plana y horizontal a la velocidad de 4
m/s. Si el coeficiente de rozamiento es 0’2. Calcular: la normal, la fuerza de rozamiento, la deceleración
producida por el rozamiento y tiempo que tarda en pararse.
29.Un coche de 1500 Kg toma una curva de radio 200 m. ¿Qué fuerza de rozamiento debe darse entre la
carretera y los neumáticos cuando el coche lleva 100 Km/h, para que no deslice?
30.A un cuerpo de 10 Kg de masa le aplicamos una fuerza de 50 N. Halla la aceleración que se le
comunica.
31.Un coche va a 72 Km/h y se le obliga a parar a los 100 m. ¿Qué deceleración hay que darle? Calcular
el tiempo que tardará en detenerse y la fuerza que ejercen los frenos. Dato: masa del coche 7500 Kg.
32.Un coche arranca con una aceleración de 0’4 m/s2. ¿Qué fuerza experimenta el conductor de 70 Kg?
Al cabo de 25 s, ¿qué velocidad posee?
33.Calcula la aceleración, velocidad al final de los 10 m de recorrido y tiempo que tarda en recorrer esos
10 m de un móvil, de 15 Kg de masa, al que se le aplica una fuerza de 75 N. Dato: coeficiente de
rozamiento 0’2.
34.Calcula la tensión de la cuerda y la aceleración del movimiento en la siguiente situación: a) si no hay
rozamiento; b) si hay rozamiento con 0’1.
M2=20 Kg
M1=10 Kg
35.Halla la aceleración del sistema y la tensión de la cuerda. Si partieron del reposo, ¿qué espacio han
recorrido en 5 s?
M1=320g
M2=110 g
36. Calcula las tensiones, normales, fuerzas de rozamiento y aceleraciones, en cada situación:
Datos: F1=1 N; m1=5 Kg; º.
F2=15 N; m2=7 Kg; º.
T=80 N; m3=10 Kg; º.