POLÍGONOS EN GENERAL

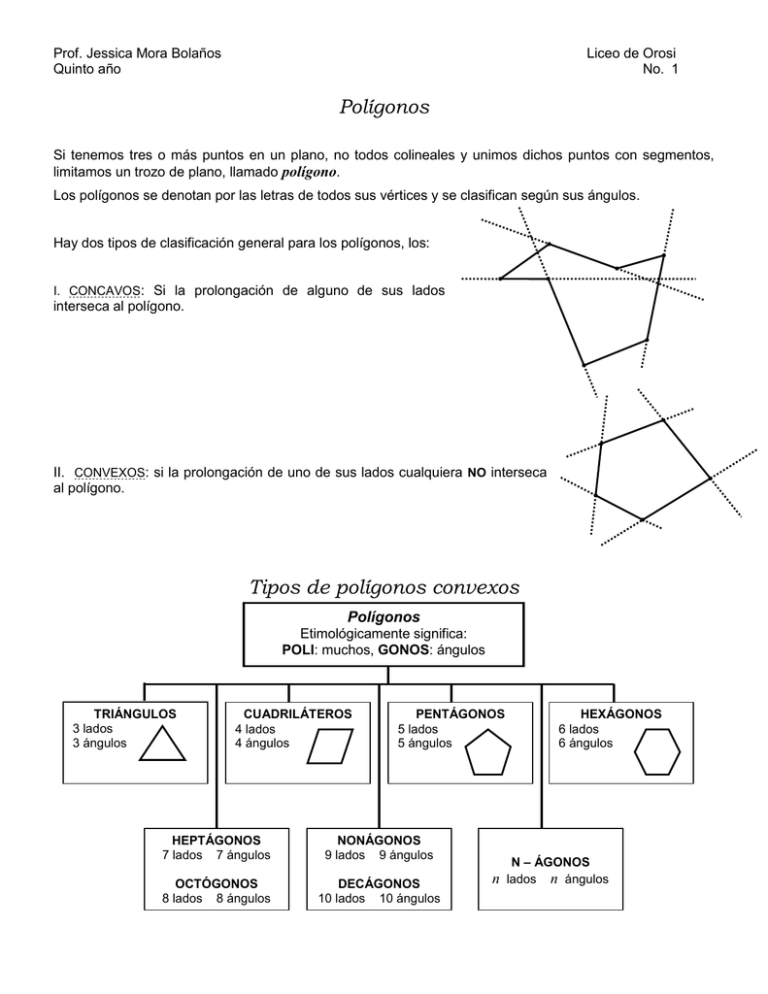
Prof. Jessica Mora Bolaños
Quinto año
Liceo de Orosi
No. 1
Polígonos
Si tenemos tres o más puntos en un plano, no todos colineales y unimos dichos puntos con segmentos,
limitamos un trozo de plano, llamado polígono.
Los polígonos se denotan por las letras de todos sus vértices y se clasifican según sus ángulos.
Hay dos tipos de clasificación general para los polígonos, los:
I. CONCAVOS: Si la prolongación de alguno de sus lados
interseca al polígono.
II. CONVEXOS: si la prolongación de uno de sus lados cualquiera NO interseca
al polígono.
Tipos de polígonos convexos
Polígonos
Etimológicamente significa:
POLI: muchos, GONOS: ángulos
TRIÁNGULOS
3 lados
3 ángulos
CUADRILÁTEROS
4 lados
4 ángulos
PENTÁGONOS
5 lados
5 ángulos
HEPTÁGONOS
7 lados 7 ángulos
NONÁGONOS
9 lados 9 ángulos
OCTÓGONOS
8 lados 8 ángulos
DECÁGONOS
10 lados 10 ángulos
n
HEXÁGONOS
6 lados
6 ángulos
N – ÁGONOS
lados n ángulos
Prof. Jessica Mora Bolaños
Quinto año
Liceo de Orosi
No. 2
Circunferencias Inscritas Y Circunscritas
Circunferencias inscritas: es cuando una circunferencia es tangente a TODOS los lados de un polígono,
y además, se dice que el polígono está circunscrito en la circunferencia.
Circunferencia inscrita
en un triángulo
equilátero
Circunferencia inscrita
en un cuadrado
Circunferencia inscrita
en un hexágono
Circunferencias circunscritas: es cuando una circunferencia pasa por los vértices de un polígono,
entonces se dice que el polígono está inscrito en la circunferencia.
Circunferencia circunscrita
a un triángulo
Circunferencia circunscrita
a un Cuadrado
Circunferencia circunscrita
a un hexágono regular
Polígono convexo regular
Es un polígono convexo EQUILÁTERO (todos los lados iguales) y EQUIÁNGULO (todos los ángulos iguales).
Los polígonos regulares más sencillos son los siguientes:
TRIÁNGULO
EQUILÁTERO
CUADRADO
PENTÁGONO
REGULAR
HEXÁGONO
REGULAR
Prof. Jessica Mora Bolaños
Quinto año
Liceo de Orosi
No. 3
Elementos de un polígono regular
Lado: cada uno de los segmentos que lo limitan. Se representa por L
Perímetro: suma de cada uno de los lados que conforman el polígono
(L + L + L + ... + L ); o bien se multiplica la medida del lado por el
número de lados que éste tenga ( n • L ). Se representa por
decir, P = n • L
Semiperímetro: es la mitad del perímetro, es decir: S =
P.
P
Es
L
r
L
a
.
2
Centro: punto desde el cual distan los vértices del polígono.
Apotema: distancia del centro del polígono al punto medio de uno de sus lados. Se
utiliza la letra “ a ” para señalar la apotema. El segmento que representa la apotema
forma un ángulo de 90° con el lado del polígono.
r
a
Radio: distancia del centro del polígono a cada uno de los vértices. Se utiliza la letra ” r
” para señalar el radio.
Ángulos en un polígono regular
Angulo central del polígono: formado por dos radios consecutivos y el centro del polígono como vértice.
Se formarán tantos ángulos centrales como lados tenga el polígono. La suma de todos los ángulos
centrales es un giro completo: 360 º.
Medida de un ángulo central =
360 º
n
;
n : número de lados del polígono.
Angulo exterior del polígono: todos los ángulo exteriores de un polígono regular son congruentes.
Todos los ángulos exteriores suman 360 º.
Medida de un ángulo exterior =
360 º
n
;
n : número de lados del polígono.
Angulo interno o interior del polígono: ángulo formado por dos lados consecutivos del polígono.
Medida de un ángulo interno:
 i=
180 º (n  2)
n
;
n : número de lados del polígono
i : ángulo interno
Suma de los ángulos internos:
Si = 180 º (n  2)
; n : número de lados del polígono.
Si : suma de los ángulos internos
Prof. Jessica Mora Bolaños
Quinto año
Liceo de Orosi
No. 4
Todos los elementos anteriores pueden verse en la siguiente representación:












: ángulo interno o interior

: ángulo exterior

: ángulo central
Número de diagonales desde un vértice: el número de diagonales desde un vértice cualquiera de un
polígono convexo, es igual al número de lados menos tres; es decir:
D v = (n  3)
;
n : número de lados del polígono.
Por ejemplo, el número de diagonales desde un vértice de un hexágono:
Número total de Diagonales de un polígono: el número total de diagonales D, que pueden trazarse
desde todos los vértices, está dado por la fórmula:
D=
n (n  3)
2
;
n : número de lados del polígono.
Por ejemplo, el número total de diagonales de un hexágono:
Prof. Jessica Mora Bolaños
Quinto año
Liceo de Orosi
No. 5
Área de un polígono regular: se obtiene al multiplicar el semiperímetro por la longitud de la apotema;
es decir:
A=
P
a
2
=
sa
PRACTICA
I. COMPLETE LA SIGUIENTE TABLA
POLÍGONO
REGULAR
TRIÁNGULO
EQUILÁTERO
CUADRADO
PENTÁGONO
HEXÁGONO
HEPTÁGONO
OCTÓGONO
NONÁGONO
DECÁGONO
11 – AGONO
12 – AGONO
13 – AGONO
14 – AGONO
15 – AGONO
20 – AGONO
25 – AGONO
30 – AGONO
100 – AGONO
#
LADOS
m
m
m
CENTRAL EXTERIOR INTERIOR
SUMA
# D.
INTERIOR VÉRTICE
# TOTAL
DIAGON.
Prof. Jessica Mora Bolaños
Quinto año
Liceo de Orosi
No. 6
II. PROBLEMAS
1. Dadas las sumas de los ángulos internos de distintos polígonos regulares, determine cual es el polígono
al que corresponde dicha suma.
(a) 900 º
(b) 1800 º
(c) 180 º
(d) 360 º
(e) 720 º
(f) 540 º
(g) 6120°
2. Determine cuál es el:
(h) polígono en el que se puede trazar como máximo 5 diagonales desde un vértice.
(i) polígono en el que se puede trazar como máximo 27 diagonales desde un vértice.
(j) polígono en el que se puede trazar 14 diagonales en total.
(k) polígono en el que se puede trazar 152 diagonales en total.
3. Si el lado de un hexágono regular mide 10cm,
(l) Determine la medida de la apotema.
(m) Halle el perímetro y el área del hexágono.
4. Encuentre la medida de la apotema de un pentágono de 12dm de lado.
5. La apotema de un cuadrado circunscrito en una circunferencia es 12 cm,
(n) Halle el perímetro del cuadrado
(ñ) Halle la medida del radio de la circunferencia inscrita en el cuadrado.
(o) Calcule el área del cuadrado y el área del círculo y determine cuál es mayor y cuán mayor es.
6. La apotema de un cuadrado mide 2dm, determine su área.
7. El radio de un triángulo equilátero mide 12cm,
(p) Determine la medida de su lado.
(q) Determine la medida de su apotema.
r
(r) Determine su área y perímetro.
8. Determine el área de un heptágono regular cuyo radio mide 5cm.
9. Calcular el área de un octógono cuyo lado mide 6dm y la apotema mide 4dm.
10. Determine el área de un pentágono regular si lado mide 8cm y su radio mide 5 cm.
11. Determine la apotema de un hexágono regular si su área es igual a 72 3 cm 2.
12. En una circunferencia cuyo radio mide 4cm,
(s) ¿Cuál es la medida de un lado del triángulo equilátero inscrito en la circunferencia?
(t)¿Cuál es la medida de un lado del hexágono regular inscrito en la misma
circunferencia?
(u) ¿Cuál es la medida de un lado de un decágono regular inscrito en la misma
circunferencia?
Prof. Jessica Mora Bolaños
Quinto año
Liceo de Orosi
No. 7
(v) ¿Cuál es la medida de un lado de un 30 - ágono regular inscrito en la misma
Circunferencia?
(w) Calcule el área del:
FIGURA
AREA
Círculo
Triángulo
Hexágono
Decágono
30-ágono
compare los resultados.
(x) Qué concluiría usted de acuerdo a los resultados obtenidos en el ejercicio (w)
13. Determine:
13.1 el perímetro y el área de un nonágono regular cuya apotema mide 8 cm.
13.2 el área de un hexágono regular cuya apotema mide 3 cm.
13.3 el área de un pentágono regular cuyo radio mide 5 cm.
13.4 la medida de un lado de un dodecágono regular cuyo radio mide 20 cm.
13.5 el número de lados de un polígono regular cuyos ángulos internos suman 1080°.
13.6 el nombre polígono regular desde el cual se puede trazar 35 diagonales en total.
13.7 el número de lados de un polígono regular desde el cual se pueden trazar 9 diagonales desde un
vértice.
13.8 la suma de los ángulos internos de un polígono regular de 50 lados.
13.9 la suma de los ángulos internos de un polígono regular sabiendo que su ángulo central mide 24º.
13.10 el nombre del polígono regular sabiendo que su ángulo exterior mide18º
14. Dado el octógono regular de centro O, determine cuál es la medida de:
 ,  ,  ,  ,  ,  ,  ,  
G
F
H


A

B



E
O


C
D