SOLUCIÓN PROBLEMAS EXAMENES TIPO A Y E .PROGRAMA NUEVO SEPTIEMBRE 20001

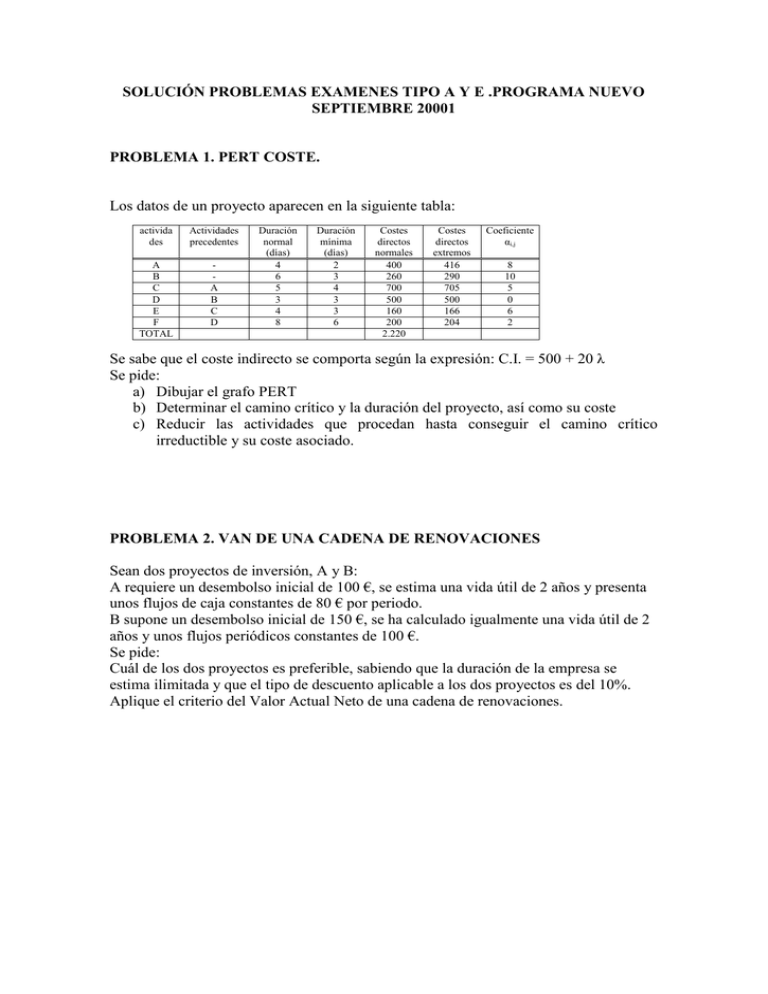
SOLUCIÓN PROBLEMAS EXAMENES TIPO A Y E .PROGRAMA NUEVO
SEPTIEMBRE 20001
PROBLEMA 1. PERT COSTE.
Los datos de un proyecto aparecen en la siguiente tabla:
activida
des
Actividades
precedentes
A
B
C
D
E
F
TOTAL
A
B
C
D
Duración
normal
(días)
4
6
5
3
4
8
Duración
mínima
(días)
2
3
4
3
3
6
Costes
directos
normales
400
260
700
500
160
200
2.220
Costes
directos
extremos
416
290
705
500
166
204
Coeficiente
αi,j
8
10
5
0
6
2
Se sabe que el coste indirecto se comporta según la expresión: C.I. = 500 + 20 λ
Se pide:
a) Dibujar el grafo PERT
b) Determinar el camino crítico y la duración del proyecto, así como su coste
c) Reducir las actividades que procedan hasta conseguir el camino crítico
irreductible y su coste asociado.
PROBLEMA 2. VAN DE UNA CADENA DE RENOVACIONES
Sean dos proyectos de inversión, A y B:
A requiere un desembolso inicial de 100 €, se estima una vida útil de 2 años y presenta
unos flujos de caja constantes de 80 € por periodo.
B supone un desembolso inicial de 150 €, se ha calculado igualmente una vida útil de 2
años y unos flujos periódicos constantes de 100 €.
Se pide:
Cuál de los dos proyectos es preferible, sabiendo que la duración de la empresa se
estima ilimitada y que el tipo de descuento aplicable a los dos proyectos es del 10%.
Aplique el criterio del Valor Actual Neto de una cadena de renovaciones.
SOLUCIÓN PROBLEMA 1:
a) Grafo PERT
C=5
2
4
8
4
9 13
E=
4
A=4
6
1
17
0 0
B=
6
5
3
6
6
D=3
9
17
F=8
9
b) Camino crítico, duración y coste:
Del grafo se desprende que el camino crítico está formado por las actividades BD-F y que su duración es de 17 días. El coste asociado a este proyecto es el
siguiente:
C.D. =
2.220
C.I. = 500 + 20 x 17 = 840
C.T. =
3.060
c) Para realizar las reducciones hay que operar con las actividades del camino
critico eligiendo en primer lugar la que presente un menor coeficiente de coste.
Reducción 1
En nuestro caso es la actividad F, ya que, la D tiene un coeficiente 0 como
consecuencia de que su tiempo normal es igual a su tiempo extremo; es decir, no
se puede realizar en menos tiempo del que tiene establecido y, por lo tanto, no se
puede reducir. Teniendo en cuenta que αF = 2, y que la máxima reducción que
podemos aplicar es de 2 días, la situación queda reflejada en el gráfico siguiente:
C=5
2
4
6
4
9
11
E=4
A=4
6
1
15
0 0
B=6
5
3
6
6
9
D=3
15
F=6
9
El camino crítico continúa siendo el mismo: B-D-F, aunque ahora la duración ha pasado
de 17 a 15 días. Los costes asociados a esta situación son:
C.D. = 2.220 + 2 x 2 = 2.224
C.I. = 500 + 20 x 15 = 800
C.T. =
= 3.024
Reducción 2
Para hacer la siguiente reducción no tenemos alternativa. El camino crítico sigue siendo
el mismo; la actividad D no se puede reducir y la F ya la hemos situado con la anterior
reducción en su tiempo mínimo de ejecución; por lo tanto, con independencia de cuál
sea su coeficiente de coste sólo podemos reducir la actividad B. Tenemos en cuenta que
αB = 10. El PERT que corresponde es el siguiente:
C=5
2
4
4
4
9
9
E=4
A=4
6
1
13
0 0
B=3
5
3
3
4
D=3
6
13
F=6
7
Puede comprobarse que ahora ha cambiado el camino crítico y ha pasado a ser A-C-E
con una duración de 13 días. Los costes de esta situación son:
C.D. = 2.224 + 10 x 3 = 2.254
C.I. = 500 + 20 x 13 = 760
C.T. =
= 3.014
Reducción 3
Ahora, como debemos actuar sobre las actividades del camino crítico, nuestro siguiente
objetivo es reducir la que tenga un menor coeficiente de coste de A-C-E. Según la tabla
del enunciado corresponde a C cuyo αC = 5. Podemos reducirla en 1 día. La situación
queda reflejada en el siguiente grafo:
C=4
2
4
4
4
8
8
E=4
A=4
6
1
12
0 0
B=3
5
3
3
3
D=3
6
12
F=6
6
Con esta reducción los dos caminos posibles son críticos; la duración del proyecto se ha
situado en 12 días, y los costes asociados son:
C.D. = 2.254 + 5 x 1
= 2.259
C.I. = 500 + 20 x 12 = 740
C.T. =
= 2.999
Ya no podemos seguir reduciendo más. Téngase en cuenta que al haber dos caminos
críticos tendríamos que reducir una actividad de cada camino, y ambas por la misma
dimensión temporal, cosa que no es factible ya que el camino B-D-F está reducido al
máximo.
Nota: Nótese que si redujéramos la actividad E que sería la que menor coeficiente de
coste presenta de las que quedan por reducir (αE = 6 y αA = 8), el coste total aumentaría.
La simulación sería la siguiente:
C=4
2
4
5
4
8
9
E=3
A=4
6
1
12
0 0
B=3
5
3
3
3
D=3
6
12
F=6
6
Como vemos, la duración total del proyecto no variaría y se seguiría manteniendo en 12
días y el coste sería:
C.D. = 2.259 + 6 x 1
= 2.265
C.I. = 500 + 20 x 12 = 740
C.T. =
= 3.005 mayor que el anterior.
Como conclusión del problema puede afirmarse que el mínimo coste total coincide con
la mínima duración posible del proyecto.
SOLUCIÓN PROBLEMA 2.
Según se explica en el capítulo 4 del libro de texto, la fórmula a aplicar para determinar
el VAN de una cadena de infinitas renovaciones es la siguiente:
 1  K n 
VANC  VAN 

n
 1  K   1
En nuestro caso tenemos dos proyectos de inversión, y en ambos K = 0,1 y n = 2; luego
en primer lugar calculamos el VAN correspondiente a cada proyecto:
 1
1 
VAN A  100  80

 38,83
2
 1  0,1 1  0,1 
 1
1 
VAN B  150  100

 23,54
2
 1  0,1 1  0,1 
Utilizando los datos anteriores y sustituyendo en la fórmula del VANC obtenemos:
 1  K n 
 1  0,12 
VANC A  VAN A 

38
,
83


  223,7
n
2




1

K

1
1

0
,
1

1




 1  K n 
 1  0,12 
VANCB  VAN B 

23
,
54


  135.6
n
2




1

K

1
1

0
,
1

1




A la vista de los resultados, se elegirá el proyecto A por tener un VANC mayor.