Un árbol es un grupo finito de nodos, donde uno de esos

ÁRBOLES
Un árbol es un grupo finito de nodos, donde uno de esos nodos sirve como raíz y el resto de los
nodos se organizan debajo de la raíz de una forma jerárquica. Un nodo que referencia un nodo
debajo suyo es un nodo padre. De forma similar, un nodo referenciado por un nodo encima de él, es
un nodo hijo. Los nodos sin hijos, son nodos hoja. Un nodo podría ser un padre e hijo, o un nodo
hijo y un nodo hoja.
Un nodo padre podría referenciar tantos hijos como sea necesario. En muchas situaciones, los
nodos padre sólo referencian un máximo de dos nodos hijos. Los árboles basados en dichos nodos
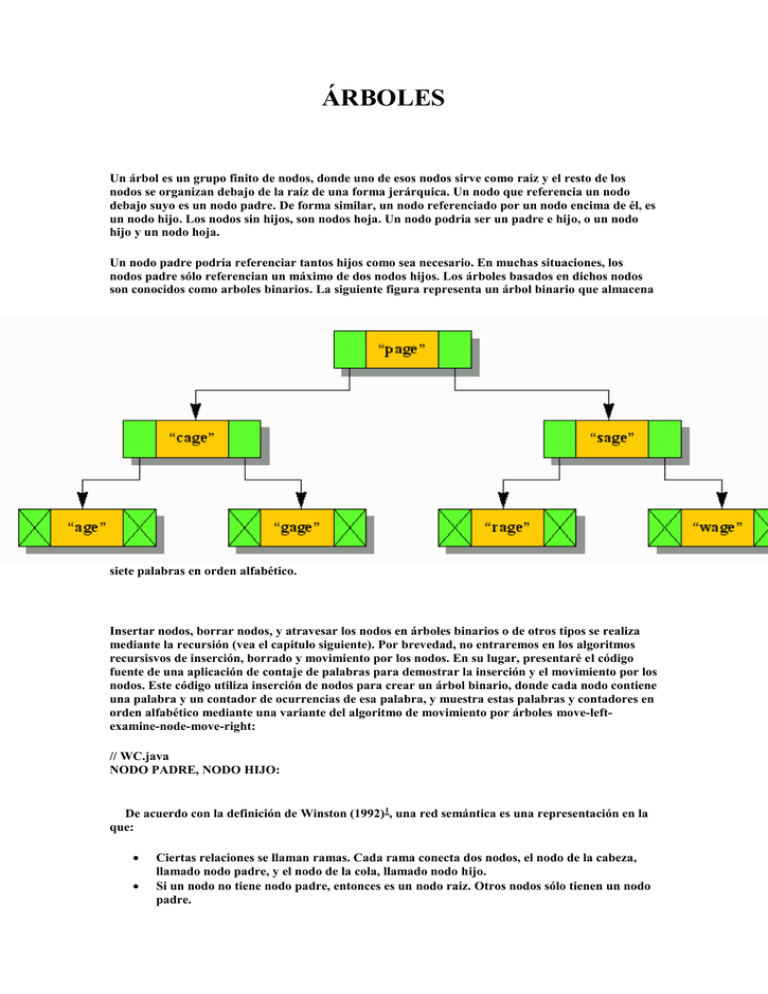
son conocidos como arboles binarios. La siguiente figura representa un árbol binario que almacena
siete palabras en orden alfabético.
Insertar nodos, borrar nodos, y atravesar los nodos en árboles binarios o de otros tipos se realiza
mediante la recursión (vea el capítulo siguiente). Por brevedad, no entraremos en los algoritmos
recursisvos de inserción, borrado y movimiento por los nodos. En su lugar, presentaré el código
fuente de una aplicación de contaje de palabras para demostrar la inserción y el movimiento por los
nodos. Este código utiliza inserción de nodos para crear un árbol binario, donde cada nodo contiene
una palabra y un contador de ocurrencias de esa palabra, y muestra estas palabras y contadores en
orden alfabético mediante una variante del algoritmo de movimiento por árboles move-leftexamine-node-move-right:
// WC.java
NODO PADRE, NODO HIJO:
De acuerdo con la definición de Winston (1992)1, una red semántica es una representación en la
que:


Ciertas relaciones se llaman ramas. Cada rama conecta dos nodos, el nodo de la cabeza,
llamado nodo padre, y el nodo de la cola, llamado nodo hijo.
Si un nodo no tiene nodo padre, entonces es un nodo raíz. Otros nodos sólo tienen un nodo
padre.




Si un nodo no tiene nodo hijo, entonces se llama nodo hoja.
Cuando dos nodos están conectados entre ellos por una cadena de dos o más ramas, uno es
el ancestro y el otro el descendiente.
Posee constructores que conectan un nodo padre con un nodo hijo con una relación
arbórea.
Posee lectores que listan los hijos de un nodo determinado o el padre de un nodo
determinado.
En ciencias de la informática, un árbol es una estructura de datos ampliamente usada que emula la
forma de un árbol (un conjunto de nodos conectados). Un nodo es la unidad sobre la que se
construye el árbol y puede tener cero o más nodos hijos conectados a él. Se dice que un nodo a es
padre de un nodo b si existe un enlace desde a hasta b (en ese caso, también decimos que b es hijo
de a). Sólo puede haber un único nodo sin padres, que llamaremos raíz. Un nodo que no tiene hijos
se conoce como hoja.
Árbol binario
De Wikipedia, la enciclopedia libre
Saltar a navegación, búsqueda
Para otros usos de este término véase Árbol binario (desambiguación).
En ciencias de la computación, un árbol binario es una estructura de datos en el cual cada nodo:




No tiene hijos (hoja).
Tiene un hijo izquierdo y un hijo derecho.
Tiene un hijo izquierdo.
Tiene un hijo derecho.
Tipos de árboles binarios [editar]








Un árbol binario es un árbol con raíz en el que cada nodo tiene como máximo dos hijos.
Un árbol binario lleno es un árbol en el que cada nodo tiene cero o dos hijos.
Un árbol binario perfecto es un árbol binario lleno en el que todas las hojas (vértices con
cero hijos) están a la misma profundidad (distancia desde la raíz, también llamada altura)
A veces un árbol binario perfecto es denominado árbol binario completo. Otros definen un
árbol binario completo como un árbol binario lleno en el que todas las hojas están a
profundidad n o n-1, para alguna n.
Un árbol casi-completo es un árbol en el que cada nodo que tiene un hijo derecho también
tiene un hijo izquierdo. Tener un hijo izquierdo no requiere que un nodo tenga un hijo
derecho. Dicho de otra forma, un árbol casi completo es un árbol donde para un hijo
derecho, hay siempre un hijo izquierdo.
Otra característica que normalmente tendrán nuestros árboles es que todos los nodos
contengan el mismo número de punteros, es decir, usaremos la misma estructura para
todos los nodos del árbol. Esto hace que la estructura sea más sencilla, y por lo tanto
también los programas para trabajar con ellos.
Tampoco es necesario que todos los nodos hijos de un nodo concreto existan. Es decir, que
pueden usarse todos, algunos o ninguno de los punteros de cada nodo.
Un árbol en el que en cada nodo o bien todos o ninguno de los hijos existe, se llama árbol
completo. En una cosa, los árboles se parecen al resto de las estructuras que hemos visto:
dado un nodo cualquiera de la estructura, podemos considerarlo como una estructura
independiente. Es decir, un nodo cualquiera puede ser considerado como la raíz de un
árbol completo.
Existen otros conceptos que definen las características del árbol, en relación a su tamaño:
Orden: es el número potencial de hijos que puede tener cada elemento de árbol. De este
modo, diremos que un árbol en el que cada nodo puede apuntar a otros dos es de orden
dos, si puede apuntar a tres será de orden tres, etc.
Grado: el número de hijos que tiene el elemento con más hijos dentro del árbol. En el árbol
del ejemplo, el grado es tres, ya que tanto 'A' como 'D' tienen tres hijos, y no existen
elementos con más de tres hijos.
Nivel: se define para cada elemento del árbol como la distancia a la raíz, medida en nodos.
El nivel de la raíz es cero y el de sus hijos uno.
Altura: la altura de un árbol se define como el nivel del nodo de mayor nivel. Como cada
nodo de un árbol puede considerarse a su vez como la raíz de un árbol, también podemos
hablar de altura de ramas.
Los árboles de orden dos son bastante especiales, de hecho les dedicaremos varios
capítulos. Estos árboles se conocen también como árboles binarios.
Frecuentemente, aunque tampoco es estrictamente necesario, para hacer más fácil moverse
a través del árbol, añadiremos un puntero a cada nodo que apunte al nodo padre. De este
modo podremos avanzar en dirección a la raíz, y no sólo hacia las hojas.
Es importante conservar siempre el nodo raíz ya que es el nodo a partir del cual se
desarrolla el árbol, si perdemos este nodo, perderemos el acceso a todo el árbol.
El nodo típico de un árbol difiere de los nodos que hemos visto hasta ahora para listas,
aunque sólo en el número de nodos.
RECORRIDO EN ÁRBOLES BINARIOS
Una de las operaciones mas importantes a realizar en un árbol binario es el recorrido de
los mismos, recorrer significa visitar los nodos del árbol en forma sistemática, de tal
manera que todos los nodos del mismo sean visitados una sola vez.
Existen 3 formas diferentes de efectuar el recorrido y todas ellas de naturaleza
recursiva, estas son:
RECORRIDO PREORDEN: En el que se procesa el nodo y después se procesan
recursivamente sus hijos.
RECORRIDO PREORDEN
 VISITAR LA RAIZ
 RECORRER EL SUBARBOL IZQUIERDO
 RECORRER EL SUBARBOL DERECHO
RECORRIDO POSTORDEN: Donde el nodo dado se procesa después de haber
procesado recursivamente a sus hijos.
Se presenta de la siguiente manera:
 Recorrer el subárbol izquierdo en orden posterior.
 Recorrer el subárbol derecho en orden posterior
 Visita la Raíz
RECORRIDO INORDEN: En este se procesa recursivamente el hijo izquierdo, luego
se procesa el nodo actual y finalmente se procesa recursivamente el hijo derecho. Puede
recorrer estructuras lineales tales como: colas, pilas y listas
Su recorrido se realiza:
 Recorre árbol izquierdo
 Recorre la raíz
 Recorre árbol derecho
Que son los árboles binarios de búsqueda?
La búsqueda en árboles binarios es un método de
búsqueda simple, dinámico y eficiente considerado como
uno de los fundamentales en Ciencia de la Computación.
De toda la terminología sobre árboles, tan sólo recordar
que la propiedad que define un árbol binario es que cada
nodo tiene a lo más un hijo a la izquierda y uno a la
derecha.Para construir los algoritmos consideraremos que
cada nodo contiene un registro con un valor clave a través
del
cual
efectuaremos
las
búsquedas.En
las
implementaciones que presentaremos sólo se considerará
en cada nodo del árbol un valor del tipo t del Elemento
aunque en un caso general ese tipo estará compuesto por
dos: una clave indicando el campo por el cual se realiza la
ordenación y una información asociada a dicha clave o
visto de otra forma, una información que puede ser
compuesta en la cual existe definido un orden.
Árboles binarios
Un árbol binario es una estructura de datos de tipo
árbol en donde cada uno de los nodos del árbol puede
tener 0, 1, ó 2 subárboles llamados de acuerdo a su caso
como:
• Si el nodo raíz tiene 0 relaciones se llama hoja.
• Si el nodo raíz tiene 1 relación a la izquierda, el
segundo elemento de la relación es el subárbol
izquierdo.
• Si el nodo raíz tiene 1 relación a la derecha, el
segundo elemento de la relación es el subárbol
derecho.como se muestran los siguientes ejemplos:
Un árbol binario de búsqueda(ABB) es un árbol binario
con la propiedad de que todos los elementos almacenados
en el subárbol izquierdo de cualquier nodo x son menores
que el elemento almacenado en x ,y todos los elementos
almacenados en el subárbol derecho de x son mayores que
el elemento almacenado en x.
La figura 1 muestra dos ABB construidos en base al
mismo conjunto de enteros:
Obsérvese la interesante propiedad de que si se listan los
nodos del ABB en inorden nos da la lista de nodos
ordenada.Esta propiedad define un método de ordenación
similar al Quicksort,con el nodo raíz jugando un papel
similar al del elemento de partición del Quicksort aunque
con los ABB hay un gasto extra de memoria mayor debido
a los punteros.La propiedad de ABB hace que sea muy
simple diseñar un procedimiento para realizar la búsqueda.
Para determinar si k está presente en el árbol la
comparamos con la clave situada en la raíz, r.Si coinciden
la búsqueda finaliza con éxito, si k<r es evidente que k,de
estar presente,ha de ser un descendiente del hijo izquierdo
de la raíz,y si es mayor será un descendiente del hijo
derecho.La función puede ser codificada fácilmente de la
siguiente forma:
#define ABB_VACIO NULL#define TRUE 1#define
FALSE 0typedef int tEtiqueta
/*Algún tipo
adecuado*/typedef struct tipoceldaABB{
struct
tipoceldaABB *hizqda,*hdrcha;
tEtiqueta etiqueta;
}*nodoABB;typedef nodoABB ABB;
Es conveniente hacer notar la diferencia entre este
procedimiento y el de búsqueda binaria.En éste podría
pensarse en que se usa un árbol binario para describir la
secuencia de comparaciones hecha por una función de
búsqueda sobre el vector.En cambio en los ABB se
construye una estructura de datos con registros conectados
por punteros y se usa esta estructura para la búsqueda.El
procedimiento de construcción de un ABB puede basarse
en un procedimiento de inserción que vaya añadiendo
elementos al árbol. Tal procedimiento comenzaría
mirando si el árbol es vacío y de ser así se crearía un
nuevo nodo para el elemento insertado devolviendo como
árbol resultado un puntero a ese nodo.Si el árbol no está
vació se busca el elemento a insertar como lo hace el
procedimiento pertenece sólo que al encontrar un puntero
NULL durante la búsqueda, se reemplaza por un puntero a
un nodo nuevo que contenga el elemento a insertar.El
código podría ser el siguiente:
void Inserta(tElemento x,ABB *t) {
if(!(*t)){
*t=(nodoABB)malloc(sizeof(struct
tipoceldaABB));
if(!(*t)){
error("Memoria Insuficiente."); } (*t)>etiqueta=x;
(*t)->hizqda=NULL;
(*t)>hdrcha=NULL;
} else if(x<(*t)->etiqueta)
inserta(x,&((*t)->hizqda));
else
inserta(x,&((*t)->hdrcha));}
Por ejemplo supongamos que queremos construir un
ABB a partir del conjunto de enteros {10,5,14,7,12}
aplicando reiteradamente el proceso de inserción.El
resultado es el que muestra la figura 2.
TERMINOLOGIA
HIJO. X es hijo de Y, sí y solo sí el nodo X es apuntado
por Y. También se dice que X es descendiente directo de
Y.
PADRE. X es padre de Y sí y solo sí el nodo X apunta a
Y. También se dice que X es antecesor de Y.
HERMANO. Dos nodos serán hermanos si son
descendientes directos de un mismo nodo.
HOJA. Se le llama hoja o Terminal a aquellos nodos que
no tienen ramificaciones (hijos).
NODO INTERIOR. Es un nodo que no es raíz ni
Terminal.
GRADO. Es el número de descendientes directos de un
determinado nodo.
GRADO DEL ARBOL Es el máximo grado de todos los
nodos del árbol.
NIVEL. Es el número de arcos que deben ser recorridos
para llegar a un determinado nodo. Por definición la raíz
tiene nivel 1.
ALTURA. Es el máximo número de niveles de todos los
nodos del árbol.
PESO. Es el número de nodos del árbol sin contar la raíz.
LONGITUD DE CAMINO. Es el número de arcos que
deben ser recorridos para llegar desde la raíz al nodo X.
Por definición la raíz tiene longitud de camino 1, y sus
descendientes directos longitud de camino 2 y así
sucesivamente.
Árboles AVL
El árbol AVL toma su nombre de las iniciales de los apellidos de sus
inventores, Adelson-Velskii y Landis. Lo dieron a conocer en la
publicación de un artículo en 1962: "An algorithm for the
organization of information" ("Un algoritmo para la organización de
la información").
Los árboles binarios de búsqueda tal y como los hemos visto,
adolecen del problema de
que en el peor de los casos pueden tender parcialmente hacia el
árbol degenerado, de manera que
la búsqueda de un elemento cualquiera puede ser de un orden
superior a O(lg n), y tender a O(n).
Este problema queda solucionado con los árboles AVL, o
balanceados en altura
Los árboles AVL están siempre equilibrados de tal modo que para
todos los nodos, la altura de la rama izquierda no difiere en más de
una unidad de la altura de la rama derecha.
Un árbol AVL es un árbol binario de busqueda en el cual para cada
nodo las alturas de los subárboles difieren a lo sumo en uno.
Factor de equilibrio
Cada nodo, además de la información que se pretende almacenar,
debe tener los dos punteros a los árboles derecho e izquierdo, igual
que los árboles binarios de búsqueda (ABB), y además el dato que
controla el factor de equilibrio.
El factor de equilibrio es la diferencia entre las alturas del árbol
derecho y el izquierdo:
Inserción
La inserción en un árbol de AVL puede ser realizada insertando el
valor dado en el árbol como si fuera un árbol de búsqueda binario
desequilibrado y después retrocediendo hacia la raíz, rotando
sobre cualquier nodo que pueda haberse desequilibrado durante
la inserción.
Extracción
El problema de la extracción puede resolverse en O(log n) pasos.
Una extracción trae consigo una disminución de la altura de la
rama donde se extrajo y tendrá como efecto un cambio en el
factor de equilibrio del nodo padre de la rama en cuestión,
pudiendo necesitarse una rotación.
Esta disminución de la altura y la corrección de los factores de
equilibrio con sus posibles rotaciones asociadas pueden
propagarse hasta la raíz
Búsqueda
Las búsquedas se realizan de la misma manera que en los ABB,
pero al estar el árbol equilibrado la complejidad de la búsqueda
nunca excederá de O(log n).
ÁRBOLES BINARIOS DE BUSQUEDA (ABB)
• Definición:
Un árbol es una estructura de datos no lineal y homogénea en el que cada elemento
puede tener varios elementos posteriores, pero tan sólo puede tener un elemento
anterior.
Buscar un elemento
•
•
•
•
Si el árbol está vacío, terminamos la búsqueda: el elemento no está en el árbol.
Si el valor del nodo raíz es igual que el del elemento que buscamos, terminamos
la búsqueda con éxito.
Si el valor del nodo raíz es menor que el elemento que buscamos, continuaremos
la búsqueda en el árbol derecho.
El valor de retorno de una función de búsqueda en un ABB puede ser un puntero
al nodo encontrado, o NULL, si no se ha encontrado.
Insertar un elemento
• Necesitamos un puntero auxiliar para conservar una referencia al padre del nodo
raíz actual. El valor inicial para ese puntero es NULL.
• Padre = NULL
• nodo = Raíz
• Bucle: mientras actual no sea un árbol vacío o hasta que se encuentre el
elemento.
Eliminar un elemento
Para borrar un elemento también nos basamos en el algoritmo de búsqueda. Si el
elemento no está en el árbol no lo podremos borrar. Si está, hay dos casos posibles:
•
•
Se trata de un nodo hoja
Se trata de un nodo rama
Ejemplo:
Árbol binario
Existen dos tipos de árboles binarios que se consideran especiales en función de ciertas
propiedades. Estos son los siguientes:
1) Árbol binario equilibrado
2) Árbol binario completo
Árbol binario equilibrado
Es un árbol en el que en todos sus nodos se cumple la siguiente propiedad:
| altura (subárbol _ izquierdo) – altura (subárbol _ derecho) | <= 1
Recorridos por árboles
Una de las cosas que debemos poder hacer con un árbol es poder movernos a través de
la información que este contiene. El modo evidente de moverse a través de las ramas de
un árbol es siguiendo las referencias de los nodos que las componen. Los recorridos
dependen en gran medida del tipo y propósito del árbol, pero hay ciertos recorridos que
usaremos frecuentemente. Se trata de aquellos recorridos que incluyen todo el árbol.
Hay 3 formas de recorrer un árbol
Pre-orden
In-orden
Post-orden
Recorrido Pre-orden (N – I – D)
En este recorrido lo primero que se obtiene o evalúa es el nodo, antes de recorrer las
ramas; posteriormente se recorre la rama izquierda y finalmente la rama derecha. El
orden es: Nodo – Izquierda – Derecha (N – I – D).
El recorrido Pre-orden de nuestro árbol de la Figura 3 es:
M–E–A–R–O–N–Q–V
Y el recorrido Pre-orden del árbol de la Figura 5 es: N – E – A – G – R – O – V
Recorrido In-orden (I – N – D)
En este recorrido se procesa la primera rama (rama izquierda), después el nodo y
finalmente la ultima rama (rama derecha). El orden es: Izquierda – Nodo – Derecha (I –
N – D).
El recorrido In-orden de nuestro árbol de la Figura 3 es:
A–E–M–N–O–Q–R–V
Y el recorrido In-orden del árbol de la Figura 5 es: A – E – G – N – O – R – V
Recorrido Post-orden (I – D – R)
En este recorrido se primero se procesan las ramas para finalmente procesar el nodo. El
orden de este recorrido es: Izquierda – Derecha – Nodo (I – D – N).
El recorrido Post-orden del árbol de la Figura 3 es: A – E – N – Q – O – V – R – M
Y el recorrido Post-orden del árbol de la Figura 5 es: A – G – E – O – V – R – N
/* ------------------------------------------------------------------------------------------EN ESTA SECCION IRIA EL TEMA OPÉRACIONES SOBRE ABB
CALCULAR NUMERO DE NODOS
COMPROBAR SI EL NODO ES HOJA
CALCULAR EL NIVEL DE UN NODO
CALCULAR LA ALTURA DE UN ARBOL
PERO NO ME FUE ENTREGADO POR EL EQUIPO, ASI QUE LO TENDRAN QUE
INVESTIGAR
-------------------------------------------------------------------------------------------------------------------- */
http://c.conclase.net/edd/index.php?cap=008#8_5
http://c.conclase.net/edd/index.php?cap=008b#8_6 Dobles
http://c.conclase.net/edd/index.php?cap=008c#8_7 equilibrados
Introducción
Un árbol AVL (llamado así por las iniciales de sus inventores: Adelson-Velskii y
Landis) es un árbol binario de búsqueda en el que para cada nodo, las alturas de sus
subárboles izquierdo y derecho no difieren en más de 1.
Rotaciones simples de nodos
Los reequilibrados se realizan mediante rotaciones.
Rotación simple a la derecha (SD):
Esta rotación se usará cuando el subárbol izquierdo de un nodo sea 2 unidades más alto
que el derecho, es decir, cuando su FE sea de -2. Y además, la raíz del subárbol
izquierdo tenga una FE de -1, es decir, que esté cargado a la izquierda.
Procederemos del siguiente modo:
Llamaremos P al nodo que muestra el desequilibrio, el que tiene una FE de -2. Y
llamaremos Q al nodo raíz del subárbol izquierdo de P. Además, llamaremos A al
subárbol izquierdo de Q, B al subárbol derecho de Q y C al subárbol derecho de P.
En el gráfico que puede observar que tanto B como C tienen la misma altura (n), y A es
una unidad mayor (n+1). Esto hace que el FE de Q sea -1, la altura del subárbol que
tiene Q como raíz es (n+2) y por lo tanto el FE de P es -2.
1. Pasamos el subárbol derecho del nodo Q como subárbol izquierdo de P. Esto
mantiene el árbol como ABB, ya que todos los valores a la derecha de Q siguen
estando a la izquierda de P.
2. El árbol P pasa a ser el subárbol derecho del nodo Q.
3. Ahora, el nodo Q pasa a tomar la posición del nodo P, es decir, hacemos que la
entrada al árbol sea el nodo Q, en lugar del nodo P. Previamente, P puede que
fuese un árbol completo o un subárbol de otro nodo de menor altura.
En el árbol resultante se puede ver que tanto P como Q quedan equilibrados en cuanto
altura. En el caso de P porque sus dos subárboles tienen la misma altura (n), en el caso
de Q, porque su subárbol izquierdo A tiene una altura (n+1) y su subárbol derecho
también, ya que a P se añade la altura de cualquiera de sus subárboles.
Rotación simple a la izquierda (SI):
Se trata del caso simétrico del anterior. Esta rotación se usará cuando el subárbol
derecho de un nodo sea 2 unidades más alto que el izquierdo, es decir, cuando su FE sea
de 2. Y además, la raíz del subárbol derecho tenga una FE de 1, es decir, que esté
cargado a la derecha.
Procederemos del siguiente modo:
Llamaremos P al nodo que muestra el desequilibrio, el que tiene una FE de 2. Y
llamaremos Q al nodo raíz del subárbol derecho de P. Además, llamaremos A al
subárbol izquierdo de P, B al subárbol izquierdo de Q y C al subárbol derecho de Q.
En el gráfico que puede observar que tanto A como B tienen la misma altura (n), y C es
una unidad mayor (n+1). Esto hace que el FE de Q sea 1, la altura del subárbol que tiene
Q como raíz es (n+2) y por lo tanto el FE de P es 2.
1. Pasamos el subárbol izquierdo del nodo Q como subárbol derecho de P. Esto
mantiene el árbol como ABB, ya que todos los valores a la izquierda de Q
siguen estando a la derecha de P.
2. El árbol P pasa a ser el subárbol izquierdo del nodo Q.
3. Ahora, el nodo Q pasa a tomar la posición del nodo P, es decir, hacemos que la
entrada al árbol sea el nodo Q, en lugar del nodo P. Previamente, P puede que
fuese un árbol completo o un subárbol de otro nodo de menor altura.
En el árbol resultante se puede ver que tanto P como Q quedan equilibrados en cuanto
altura. En el caso de P porque sus dos subárboles tienen la misma altura (n), en el caso
de Q, porque su subárbol izquierdo A tiene una altura (n+1) y su subárbol derecho
también, ya que a P se añade la altura de cualquiera de sus subárboles.