Bibliografía - Departamento de Matemática Educativa

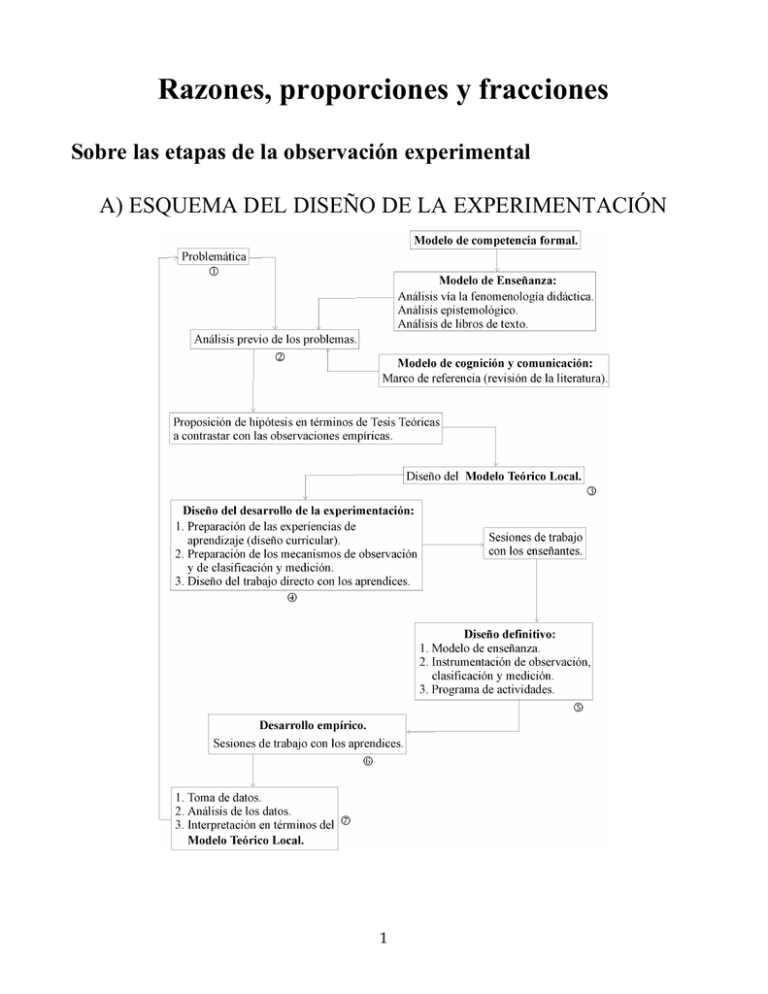
Razones, proporciones y fracciones
Sobre las etapas de la observación experimental
A) ESQUEMA DEL DISEÑO DE LA EXPERIMENTACIÓN
1
Sobre el desarrollo de la experimentación
B) ESQUEMA DEL DESARROLLO DE LA EXPERIMENTACIÓN
2
Sobre la recursividad en el uso de los modelos teóricos locales.
Nótese que en el esquema A) hay una recurrencia: empezando en el
cuadro de la problemática, al final de todo el proceso, se vuelve a él.
En el caso del esquema B), se parte de un modelo teórico local,
diseñado en las cinco primeras etapas del esquema A) y, después de
haberse hecho un estudio experimental, en que las tesis de ese
primer MTL se confrontaron con lo que ocurre en el desarrollo
empírico de la experimentación, se llega, finalmente, a una fase de
análisis e interpretación; a partir de sus resultados, la problemática
inicial se enmarca en la perspectiva de un nuevo MTL cuyo diseño
vuelve a las primera fases del esquema A), para poder iniciar,
nuevamente, el proceso descrito en el esquema B).
El Teorema de Tales; significado y sentido en un Sistema
Matemático de Signos.
El objetivo de este estudio es el de observar las obstrucciones
naturales a la utilización de un SMS en el que se puedan presentar
las nociones de variación proporcional geométrica. El análisis se
centra en la observación de los alumnos cuando se les presentan
situaciones que simulan la demostración del teorema de Tales.
Concerniente a las dos lecturas posibles, en dos SMS diferentes, se
concluye que una de ellas es irreductible a la otra. Una lectura se
3
hace con el modelo Egipcio y otra con el modelo Griego para los
números racionales. Todo ello usando la noción de significado,
contrastándola con la de sentido de un texto que utiliza un SMS
determinado.
El marco aritmético de referencia.
Los adolescentes, al comenzar el estudio del álgebra y la
trigonometría traen consigo las nociones y los enfoques que
usaban en aritmética. Sin embargo, el álgebra y la trigonometría
no son simplemente una generalización de la aritmética.
Aprender estas nuevas materias no es meramente hacer explícito
lo que estaba implícito en la aritmética. Se requiere un cambio en
el pensamiento del estudiante de las situaciones numéricas
concretas a proposiciones más generales sobre números, figuras
y operaciones. La transición desde lo que puede considerarse
como un modo informal de representación y de resolver
problemas, a uno formal resulta ser difícil para muchos de los
que comienzan a estudiar álgebra y geometría. Estos estudiantes
siguen usando los métodos que les funcionaban en aritmética.
4
DESCRIPCIÓN GENERAL
Vamos a explorar la idea teórica de que la adquisición de nuevas
competencias en la matemática elemental se puede considerar
como el producto de la modificación de conceptos, acciones y
procedimientos de SMS cuyas competencias ya son dominadas
en algún grado. Con este acercamiento, estamos simplificando
algunas observaciones de L. Wittgenstein (1964) acerca de lo que
él piensa sobre el pensamiento matemático; nosotros, aquí, sólo
estaremos presentando algunos procesos cognitivos que se
desarrollan durante su aprendizaje y por ende su enseñanza.
Observaciones como las que hemos descrito con anterioridad y
las que siguen inclinan a considerar las situaciones de enseñanza,
incluyendo aquellas en las que se realizan demostraciones
matemáticas, como la fuente de nuevos conceptos al establecer o
cambiar los significados del SMS en que se describa lo enseñado.
Esta idea está en marcado contraste con lo que los matemáticos
(en su mayoría platonistas) alegan con el punto de vista de que
las pruebas efectúan una exploración en un mundo de conceptos
preexistentes.
Así, al observar cómo se aprende matemáticas, se presenta que
siempre se están formando nuevas reglas al encontrar nuevos
5
caminos
que
extiendan
redes
conceptuales
anteriormente
desarrolladas. Un aspecto medular de este punto de vista es la
idea de sentido en contraste con la de significado, cuando se
habla de SMS estratificados.
Variación Proporcional, el Teorema de Tales; este Estudio.
El Teorema de Similaridad, también conocido como teorema de
Tales, representa un corte didáctico para la adquisición de
competencias para el uso de conceptos matemáticos importantes
que van desde las primeras nociones de algunos modelos de los
racionales hasta las propiedades de la variación continua lineal;
desde
la
introducción
de
las
funciones
lineales
y
su
representación algebraica hasta su uso en la representación
geométrica en la trigonometría y los inicios del cálculo
infinitesimal.
En este inciso, se da cuenta de un estudio experimental cuyo
principal objetivo es explorar cuáles son las competencias
necesarias para comprender y utilizar el teorema de Tales, las
obstrucciones naturales que se presentan y la importancia que
todo esto tiene para que los números racionales se expandan a un
SMS estratificado, donde los signos numéricos tengan como
referentes, tanto a las fracciones que se utilizan en el SMS de la
6
aritmética elemental, como a los signos geométricos que
denominamos razones entre magnitudes continuas. A partir de
esos resultados, se puede observar, de manera nítida, que hasta
que un usuario no tenga una correcta interpretación de todos los
conceptos que están involucrados en el teorema de similaridad,
aglutinados en los estratos de un nuevo SMS, el usuario no puede
contar con nociones estables, con las cuales pueda operar y
establecer relaciones de orden, que pueda usar de la misma
manera como lo hace con los SMS más primitivos, utilizados en
las
representaciones
de
los
números
racionales
que
se
introdujeron, anteriormente, con el uso competente del SMS de
la aritmética elemental.
Para observar el mencionado corte didáctico, se puso en
operación un diseño experimental donde la enseñanza fue
controlada por un período de dos años escolares consecutivos, en
el primero y segundo de los años de la escuela secundaria
mexicana (12 a 14 años). En esta experiencia, se controlaron las
secuencias didácticas con las que le enseñó a dos generaciones
de 30 alumnos del Centro Escolar “Hermanos Revueltas” de la
Ciudad de México. Se diseñó un test diagnóstico con tres ejes:
operatividad, competencia en la resolución de ecuaciones
7
lineales, y un último eje sobre los conceptos y ecuaciones
relacionados con el entendimiento de la situación geométrica en
que se analiza una escalera de rampa lineal, cuyo punto central y
culminante es el uso de la noción de pendiente de una recta (la
rampa en el caso concreto aquí aludido). El primer diagnóstico se
aplicó al final del primer año de la escuela secundaria, cuando
los alumnos tenían trece años. La población observada se
clasificó de acuerdo con los tres ejes descritos líneas arriba, para
así poder llevar a cabo un estudio de casos, por medio de
entrevistas videograbadas. Dos sujetos fueron seleccionados de
cada una de las clases. En las entrevistas, la primera parte se
utilizó para confirmar el diagnóstico y comprobar que se trataba
efectivamente del caso previsto previamente.
Subsecuentemente, se observaron las dificultades que se
presentaban cuando los estudiantes estaban tratando de usar la
noción de pendiente de una línea recta. La entrevista clínica
consistía, también, en la instrumentación de una secuencia
didáctica en la que los estudiantes analizaban diversas
situaciones planteadas en términos de la construcción y uso de
escaleras rectas. De los diversos conceptos, ideas y acciones que
se realizaban, algunos favorecían el uso de un nuevo estrato de
8
SMS, mientras que otras se revelaban como verdaderas
obstrucciones a la posibilidad de utilizar los nuevos signos de
manera competente para desencadenar procesos de solución
correcta
de las situaciones problemáticas presentadas o
planteadas por los alumnos en sus procesos de análisis.
Al año siguiente, se realizaron nuevas entrevistas con los casos
que resultaron más interesantes, para observar qué tipos de
obstrucciones estaban todavía presentes y cuáles habían seguido
algún tipo de evolución que permitiera la adquisición de las
competencias deseadas por la Componente Formal del Modelo
Teórico Local con el cual se estaban codificando, analizando e
interpretando los comportamientos de los alumnos, cuando se
enfrentaban a las situaciones problemáticas que se proponían
para adquirir la estructuración de las competencias, tal como lo
proponía la Componente de Enseñanza del Modelo Teórico
Local. Para estas entrevistas, por tanto, se diseñaron situaciones
problemáticas del mismo tipo que las que se habían utilizado el
año anterior. Una diferencia importante se presentó al poderse
observar, en diferentes casos, la posibilidad de dar explicaciones
generales de por qué se mantenía constante la pendiente de la
rampa, a pesar de que se calculara (en términos aritméticos) en
9
diversos puntos de la escalera. Un avance todavía más importante
se presentó con aquellos sujetos que el diagnóstico había
señalado como más hábiles en sus antecedentes de uso de las
competencias que presentaron los tres ejes del test diagnóstico.
Tal avance se lograba utilizando el SMS de la aritmética
elemental, al que se le habían adicionado los signos geométricos
que tenían que ver con la comparación de magnitudes, las
propiedades de la variación de la pendiente, y otras nociones
geométricas como ángulo de inclinación, medición de segmentos,
operaciones elementales con ellos; en fin, con el uso de un nuevo
SMS estratificado, con el cual podían darse explicaciones
intrínsecas (dentro del nuevo SMS) que explicaban la estabilidad
de la pendiente de la recta, dando cuenta de los sentidos que el
sujeto otorgaba a la serie de procesos de análisis de las
situaciones problemáticas que desencadenaba, cada vez que se
llegaba a una solución correcta. Tal descripción del sentido, en
resumidas cuentas, estructuraba los pasos que se pueden dar para,
en los ejemplos concretos planteados por la secuencia didáctica,
llevar a cabo una demostración del teorema de Tales cuando las
magnitudes involucradas son conmensurables (en el caso de las
situaciones concretas en las que aparecían los escalones de las
escaleras, en ellas, era posible medir todas las magnitudes
10
pertinentes con alguna unidad del sistema métrico decimal, los
centímetros, por ejemplo).
ALGUNAS OBSERVACIONES PARTICULARES
En esta Sección, vamos a usar términos como modelos Egipcio y
Griego de los números racionales. A grosso modo, el primero de
éstos utiliza un estrato de SMS en que los números racionales
son concebidos como partes iguales de todos discretos o
continuos; pero, donde las fracciones representan la relación
entre la parte y el todo que la contiene. Esta relación se transfiere
a otros todos con sus correspondientes partes a través de lo que
se llama equivalencia de fracciones, entendida ésta como una
proporción aritmética.
Con este Modelo, en la segunda serie de entrevistas en el estudio
de casos, se incluyó una parte de la observación que apuntaba a
medir la competencia en el uso de la unidad de medida y la
relación entre dos magnitudes cuando éstas han sido medidas,
aunque las unidades de medida sean diferentes.
El Modelo Griego es un estrato de SMS que se desarrolla a partir
del lenguaje usual para designar magnitudes lineales, la noción
de orden entre ellas, la comparación entre dos magnitudes en que
11
se introduce la noción de razón y, finalmente, la variación de una
magnitud respecto de otra. Así, el estrato de lenguaje en el que se
puede describir una situación que ilustre la noción de pendiente
de una línea recta, presupone un uso competente de un SMS (con
una fuerte componente geométrica) en el que se encuentren las
operaciones entre razones y en el que el concepto de
proporcionalidad geométrica se haya dominado al punto en que
las razones se expresen como “objetos” estables. Su uso permite
la introducción de funciones lineales continuas y el comienzo de
su uso como objetos nuevos con los cuales uno tendrá que
aprender a realizar nuevas operaciones.
Observaciones
a) Todos los estudiantes cometieron el error de lectura (que
puede considerarse natural) cuando se les hacía la pregunta P
(acerca del problema geométrico que plantea la rampa de una
escalera recta) que sigue a continuación:
“Compare la razón entre lo subido y lo avanzado en A con la
razón entre lo subido y lo avanzado en B ”.
12
¿Cuál es la relación entre
las razones
AA'
OA'
y
BB '
?
OB '
P)
¿Son iguales o es una
mayor que la otra?
La respuesta “natural” era que la segunda era mayor dado que
AA'  BB' y OA'  OB' .
Esta centración (véase, más delante, las tendencias cognitivas 5
y 6) en la que el orden entre magnitudes lineales se transfería al
orden entre razones, vía el modelo de enseñanza, tenía que ser
rectificada por la lectura aritmética (vía el modelo Egipcio) de
la situación problemática planteada. Tal rectificación sólo fue
alcanzada por algunos estudiantes, todos pertenecientes a la
clase más alta que se había obtenido a partir de la clasificación
diagnóstica arriba presentada.
Lo que es más, este error se transfiere, al hacer la misma
pregunta, cuando una de las magnitudes se aumenta mientras
las otras permanecen constantes. Esto sólo ocurre en el modelo
13
Griego, porque la misma pregunta en el modelo Egipcio se
contestó correctamente. Si fuéramos a mostrar hechos que
indiquen que la lectura aritmética y la lectura geométrica de la
situación eran irreducibles una a la otra, este ejemplo parece
ser uno de ellos.
b) Cuando se introducen los escalones de una escalera recta,
construidos en una rampa, la pregunta en el lenguaje
geométrico puede traducirse a preguntar por la relación entre
las medidas de lo subido (tomando el peralte como la unidad),
y la medida de lo avanzado, (tomando la huella como la
unidad). Y así, para todo punto A , cuando termina un escalón.
AA' #  A  Peralte

OA' #  A  Huella
Donde #  A es el número
de escalones de O a A .
Esta nueva lectura de la situación no logró ser pertinente
respuesta correcta de la pregunta P, dado que la centración
persiste, aun cuando el estudiante acababa de descubrir que las
14
fracciones que aparecen en el análisis aritmético de la situación
eran
equivalentes.
encontraban
Incluso,
frente
a
cuando
sus
ojos,
BB '
OB '
repetidamente contestaron que
estos
todos
resultados
los
se
estudiantes
era mayor porque BB' y
OB' eran más grandes.
c) Quienes rectificaron sus errores realizados en la situación
didáctica de la entrevista lo hicieron con la introducción de la
medida del peralte y de la huella, y contestando que los
números racionales
BB '
OB '
y
AA'
OA'
eran ambos reducibles al mismo
número decimal, al dividir el numerador por el denominador.
d) Cuando se dieron cuenta de que habían predicho (en la lectura
geométrica) algo que la lectura aritmética contradijo, los
estudiantes del estrato alto rectificaron su equivocación.
Tendieron
a
dar
explicaciones
geométricas
generales,
declarando que el escalón es el mismo en cada punto sobre la
escalera, porque la rampa es recta y “esta línea recta continúa
de la misma forma”. Debemos señalar nuevamente, que aunque
se usa la misma notación, tanto en el modelo Griego como en
el modelo Egipcio (a saber a b ) para designar los números
racionales que aparecen en ambos estratos del lenguaje, tales
15
objetos no son los mismos, dado que sus significados son tan
diferentes que si unos mismos hechos son descritos en ambos
estratos del lenguaje, la afirmación en uno de ellos contradice
lo que se asevera en el otro.
e) Los estudiantes que participaron en la segunda entrevista
tenían aproximadamente 14 años y estaban familiarizados con
la situación de enseñanza -el análisis de la situación de la
escalera recta (ya hecha durante el primer año de instrucción)
era para habilitarlos en producir textos y resolver las siguientes
ecuaciones aritméticas: A     B ,

B .
A C
  A  B,
 
A
B
C y
Donde A , B , C y D eran números racionales
cualesquiera. También, al mismo tiempo, supieron que la
relación
AA'
OA'
era constante en la rampa, denominándola
pendiente de esa línea recta. A pesar del conocimiento de las
afirmaciones del teorema de Tales en esta situación particular,
los estudiantes continuaron con el mismo género de centración
durante la lectura geométrica. Podemos afirmar, por eso, que la
familiaridad con las afirmaciones del teorema de Tales no es
pertinente para desarrollar la competencia que implica
contestar la pregunta P.
16
f) Algunos de los sujetos de esta edad, del estrato medio, según
la
clasificación
del
diagnóstico,
pudieron
alcanzar
la
rectificación deseada, no al dar una explicación geométrica
general pero al interpretar la situación a través de la lectura
aritmética. Esencialmente, la interpretación de la línea recta
como una rampa de una escalera recta le permitió, dado dos
puntos A y B , construir una escalera con escalones iguales en
la que
A
y
B
definían escalones. Aquí, se usa la
conmensurabilidad de las magnitudes involucradas, dado que
siempre se midieron en unidades del sistema métrico decimal y
uno siempre podría imaginar los escalones del tamaño de la
unidad más pequeña que se podía utilizar. Así, es posible
OA
OB
convertir OA' y OB' en números racionales cuyos numeradores
sean un múltiplo de la medida de la huella y cuyos
denominadores sean el mismo múltiplo; pero, esta vez del
peralte. Esta interpretación y la lectura de P en este contexto es
en términos concretos una demostración intuitiva del teorema
de Tales en el caso descrito.
g) Parte del estudio aun por concluirse indica que la variación
proporcional con magnitudes discretas es un antecedente
necesario para llegar a las conclusiones como las que se
17
describen en f). El reconocimiento de la variación lineal
OA
continua representada por la ecuación AA'  k cuando A varía
requiere de una interpretación de la pendiente de la línea recta
tal como en f). La posibilidad de representar líneas a través del
plano cartesiano, con expresiones algebraicas (ecuaciones
lineales), requiere de un dominio de la variación lineal
continua. Esto es esencial para entender la posibilidad de tener
dos variables continuas relacionadas, tales como las que se
describen con ecuaciones como y  kx (la x y la y que varían
en forma proporcional directa) y que se puede representar
como líneas rectas a través de la traducción de la geometría
analítica.
18
DISCUSIÓN FINAL. Significado y Sentido.
Para los estudiantes involucrados en este estudio, el sentido es
conferido, en el nuevo SMS, por la utilización de nuevos signos
de las maneras que los requieren cada uno de los pasos del
proceso de análisis y resolución, visto todo el sistema de signos
ligado por la concatenación de acciones desencadenadas por el
proceso de solución de las diversas situaciones problemáticas
que, con anterioridad, se consideraban irreducibles unas a las
otras y que, ahora, gracias al uso del nuevo SMS, se resuelven
con procesos que se establecen como los mismos, esto es, se
transfieren de la resolución de un problema a otro, convirtiendo
lo que antes era una diversidad de problemas en lo que, ahora, se
puede llamar una familia de problemas, cuyos miembros todos se
pueden resolver con el mismo proceso.
Los sujetos todavía no competentes en el uso del nuevo SMS,
correspondiendo a otras clases de casos, emanadas de la
clasificación diagnóstica, podían realizar el encadenamiento de
los diversos pasos requeridos por la resolución, porque
recordaban la secuencia que proponía el modelo de enseñanza;
pero, la mayoría de las veces, lo hacían sin sentido y, ante
cualquier pequeña obstrucción o variación de la situación
19
problemática, volvían a utilizar proposiciones que ya con
anterioridad habían reconocido como erróneas; sólo al contar con
los sentido que la prueba concreta del teorema de Tales les había
proporcionado, sólo entonces adquiría estabilidad el concepto de
pendiente de una recta. Tales sentidos (de uso) proveían, al
nuevo SMS, de signos más abstractos, porque tales signos tenían
como referentes a signos de una mayor cantidad de estratos del
SMS, relacionados unos con otros de la manera que se presentó,
líneas arriba, al hablar, en general, de estratos más abstractos de
SMS y del proceso cognitivo de abstracción.
20
TENDENCIAS COGNITIVAS. USO COMPETENTE DE
SISTEMAS MATEMÁTICOS DE SIGNOS (SMS) MÁS
ABSTRACTOS
UNO. La presencia de un proceso de abreviación de los textos
concretos para poder producir reglas sintácticas nuevas.
Considérese el Primer episodio; pero sobre todo el Cuarto
episodio y el Comentario 3 (también, véase Filloy y Rojano
(1989) y el Paso H).
DOS. La dotación de sentidos intermedios. Véase el Comentario
2. El análisis del Paso L, hecho en el Comentario 3. El
proceso descrito en el Paso O.
TRES. El retorno a situaciones más concretas, cuando se
presenta una situación de análisis. Este hecho está siempre
presente en la mayoría de las acciones del pensamiento
matemático y ha
sido reportado en
muchas otras
investigaciones Filloy y Rojano (1984, 1985a, 1985b, 1989).
En lo antes descrito, se puede observar en el Paso F y sobre
todo en el Paso J, donde hay un retorno a utilizar partes del
modelo concreto que ya se habían descartado en los pasos
anteriores. También, el retorno a una situación más concreta
se observa en el Paso M.
21
CUATRO. La imposibilidad de desencadenar operaciones que
podían hacerse momentos antes. Véase Filloy (1990),
donde se describe un comportamiento de este estilo al tratar
de resolver la ecuación Ax = B. En Filloy y Lema (1985), se
presentan situaciones en las que la operatividad de las
fracciones es inhibida por la presencia de lecturas
espontáneas erróneas de tipo geométrico acerca de las
nociones de razón y proporción de magnitudes, en una
secuencia de enseñanza donde la prueba del Teorema de
Thales es el hilo conductor para dotar de nuevos sentidos a
los usos de conceptos englobados en la aritmética de las
fracciones. Véase también el Paso F, en el que cuando
ecuaciones aritméticas (Ax = B), cuya operatividad estaba
totalmente dominada por toda la población, se presentan en
la cadena de pasos antes descrita, la mayoría de los
estudiantes pierden su gran habilidad operatoria para
resolver tales ecuaciones.
CINCO. Centración en lecturas hechas en estratos del lenguaje
que no permitirán resolver la situación problemática.
Véase, de nuevo, en Filloy (1990), la observación sobre el
desempeño de los estudiantes de 12 a 13 años al tratar de
22
resolver situaciones problemáticas basadas en la resolución
de la ecuación Ax = B. También, en Filloy y Lema (1985)
puede encontrarse un ejemplo de centración en la lectura
geométrica errónea acerca del orden de magnitud entre
razones de magnitudes. En lo descrito anteriormente, este
comportamiento también puede encontrarse en el Paso F o
en el Paso I, sobre todo por lo aseverado en el Comentario 2
acerca de la dependencia del sentido del contexto concreto
en que se produce el “centramiento” aludido.
SEIS. La articulación de generalizaciones erróneas. La literatura
acerca de la ejecución de errores por parte de los estudiantes
está saturada de este comportamiento. El sujeto tiende a
zafarse del comportamiento descrito en CINCO, a base de
elevar una regla a otros contextos en los que no tiene sentido
su aplicación, se trata de un uso incorrecto de tales conceptos
y operaciones.
SIETE. La presencia de mecanismos apelativos que centran el
desencadenamiento de procesos erróneos de resolución.
En muchos casos, ciertos sujetos no pueden resolver
adecuadamente lo descrito en el Paso F debido a esta
conducta. Por ejemplo, cuando los sujetos tratan de encontrar
23
el lado de un rectángulo conocida el área y la medida de la
base, utilizando el tanteo numérico, en vez de utilizar la
operación división. Muchos de los fenómenos presentados en
NUEVE se deben también a este comportamiento.
OCHO. La presencia de mecanismos inhibitorios. En un caso
extremo, los de SIETE son ejemplos típicos de este
comportamiento; pero, también en el ámbito de la resolución
de ecuaciones, la presencia de soluciones negativas da lugar
a obstrucciones de reglas sintácticas ya dominadas. La
insistencia en no empezar a analizar un problema, el negarse
a resolver ecuaciones simples en que aparecen radicales, la
incapacidad de utilizar, en los pasos intermedios de una
cadena analítica para resolver un problema, hechos
sintácticos poco dominados, etc. son más ejemplos de este
comportamiento.
NUEVE. La presencia de obstrucciones provenientes de la
semántica sobre la sintaxis y viceversa. Al resolver
problemas y dotar de significados a los signos algebraicos,
esto predispone al sujeto a la utilización de la sintaxis. La
mayoría de los fenómenos descritos en CUATRO se pueden
interpretar de esta manera. Incluso, se da el caso de que el
24
sujeto escriba una ecuación aritmética simple (en medio de
la resolución de un problema) y no la reconozca como tal,
aunque lleve años resolviéndola con gran destreza. En el
caso de la sintaxis, la tendencia a centrarse en estratos más
concretos de uso inhibe lecturas adecuadas de los textos más
abstractos.
DIEZ. La generación de errores sintácticos debido a la
producción de códigos personales intermedios, para
dotar de sentidos a las acciones concretas intermedias.
Considérese el Paso I y el Comentario 3. También, en Filloy
y Rojano (1989), hay una descripción de esta tendencia
cognitiva. Ahí mismo puede observarse como esto puede
generar errores de sintaxis.
ONCE. La necesidad de dotar de sentidos a las redes de acciones
cada
vez
más
abstractas
hasta
convertirlas
en
operaciones. Todos los pasos de la entrevista clínica se
conjugan como ejemplo de esta aseveración.
25
Bibliografía
Alarcón, J.; Figueras, O.; Filloy, E.; Gispert, M.; Lema, S.; Parra, B.M.; Recio, J.; Rojano, T.; Zubieta,
G.Matemáticas 100 horas. 1 y 2. Fondo Educativo Interamericano, México, Bogotá, Caracas,
Santiago, San Juan y Panamá, 1981-1982.
Arraghi, G. (1965). Leonardo Pisano e i tempi suoi. Bollettino dell'Accademia degli Euteleti N. 37 pp. 75-89.
Arraghi, G. (1966). Leonardo Fibonacci: La Practica di Geometria. Testimonianze di Storia della
Scienza N. 3, Pisa Domus Galilaeana.
Boncompagní, B. Intorno ad Alcune Opere di Leonardo Pisano, matematico del secolo decimoterzo.
Tipografía delle Belle Arti, Roma 1954.
Bombelli, da Bologna, Rafael. L’Algebra. Editoriale Feltrinelli, Milano, 1963.
Boyer,C.B. A History of Mathematics. John Wiley, New York, 1968.
Boyer,C.B. The History of the Calculus. John Wiley, New York, 1959.
Brousseau, G. (1986). Fondements et méthodes de la didactique des mathématiques,
Recherches en Didatique des Mathématiques, Vol. 7, pp. 33-115.
(Calandri, P.M.) Arrighi G. Tractato D’Abbacho. Domus Galileana, Pisa, 1974.
Carmichael, R. (1959). The Theory of Numbers and Diophantine Analyssis. Dover.
Clagett,M. Nicole Oresme and the Medieval Geometry of Qualities and Motions. The University of
Wisconsin Press. Madison, Milwakee and London, 1968.
Clagett, M. The Science of Mechanics in the Middle Ages. The University of Wisconsin Press.
London, 1959.
Cuevas, O. (1994). Proyecto de Doctorado: Problemas de transferencia en modelos de
enseñanza que utiliza, a la vez, múltiples representaciones. Departamento de Matemática
Educativa del CINVESTAV-IPN.
Cummins, R. Meaning and Mental Representation.
(Diofanto de Alejandría). Vera, F. Científicos Griegos (Recopilación, Estudio Preliminar,
Preámbulos y Notas). Vol. 2, Editorial Aguilar, México, 1970.
Eco, U. 1995. Tratado de semiótica general, Barcelona: Lumen.
Egmond,W.V. Practical Mathematics in the Italian Renaissance (A catalog of Italian Abbacus
Manuscripts and Printed Books to 1600).
Suplemento agli Annali dell’Instituto e
Museo di Storia della Scienza 1980. Fascicolo 1. Instituto e Museo di Storia della Scienza,
Firenze, 1980.
(Fibonacci of Pisa, Leonardo), Boncompagni, Baldassarre. Scritti di Leonardo Pisano, vol. 2, Rome,
1857.
Filloy, E. Investigación en Matemática Educativa en México. Un reporte. Recherches en
Didactique des Mathématiques, Vol.2, No. 2, pp. 223-256. Francia. 1981.
Filloy, E., 1986. Teaching Strategies for Elementary Algebra and the Interrelationship between the
Development of Syntactic and Semantic Abilities, in (ed.) Proceedings of the Eighth Annual
Meeting for the Psychology of Mathematics Education, North American Chapter. pp. 108-113.
East Lansing, Michigan, USA.
26
Filloy, E., 1990. PME Algebra Research. A Working Perspective, in G. Booker, P. Cobb and T.
Mendicuti (eds.) Proceedings of the Fourteenth Annual Conference for the Psychology of
Mathematics Education. Vol. 1, pp. PII1-PII33. Oaxtepec, México.
Filloy, E. (1991). Cognitive Tendencies and Ababstraction Processes in Algebra Learning. Memorias
de la XV Reunión del PME Vol. II, pp. 48-55, Genoa, Italia.
Filloy, E., 1991a, Cognitive tendencies and abstraction processes in algebra learning, in F. Furinghetti
(ed.) Proceedings of the Fifteenth Annual Conference for the Psychology of Mathematics
Education. Vol. 2, pp. 48-56. Assisi, Italy.
Filloy, E., 1991b, El Libro de los Cuadrados de Leonardo de Pisa, en T. Rojano, E. Filloy y L. Puig
(eds.) Historia de las ideas algebraicas. Memorias del Tercer Simposio Internacional sobre
Investigación en Educación Matemática, pp. 11-30.
Filloy, E. History-Epistemology-Mathematical Didactics. Paper presented at the Nineth Conference for
the Psychology of Mathematics, International Group. Noordwijkerhout, The Netherlands, 1985.
Filloy, E. Teaching Strategies for Elementary Algebra and the Interrelationship between the
Development of Syntactic and Semantic Abilities. Proceedings of the Eighth Annual Meeting
for the Psychology of Mathematics, North American Chapter. East Lansing, Michigan, 1986,
pp. 108-113.
Filloy, E. (1987). Modelling and the teaching of algebra, , in J. Bergeron, N. Hercovics and C.
Kieran (eds.), Proceedings of the Eleventh Annual Meeting for the Psychology of
Mathematics Education, Vol. 1, pp. 295-300. Montreal, Canada.
Filloy, E. (1990). PME Algebra Research. A Working Perspective, in J. Bergeron, N. Hercovics
and C. Kieran (eds.), Proceedings of the Eleventh Annual Meeting for the Psychology of
Mathematics Education, Vol. 1, pp. 295-300. Montreal, Canada.
Filloy, E.: 1990, PME algebra research. A working perspective, Proceedings of the XIV Annual
Meeting of PME, pp. PII. 1-31, Vol. 1, Oaxtepec, Morelos, México.
Filloy, E. (1991). Cognitive tendencies and abstraction processes in algebra learning, en
Furinghetti (ed.), Proceedings of Fifteenth Annual Conference for the Psychology of
Mathematics Education, Vol. 2, pp. 48-56. Assisi, Italy.
Filloy, E. (1993). El Libro de los cuadrados de Leonardo de Pisa, en T. Rojano, E. Filloy y L.
Puig (eds.), Historia de las ideas algebraicas. Memorias del tercer Simposio
Internacional sobre Investigación en Educación Matemática. PNFAPM -SEP/DMECINVESTAV. pp. 11-30.
Filloy, E. 1990. PME Algebra Research. A Working Perspective. In Booker, G.: Coob, P. and
Mendicutti T. N., eds Proceedings of the Fourtheenth PME Conference. México, vol. I, pp. PII.
1-PII.33.
Filloy, E. (1997). Cómo dirigir una tesis doctoral. México. En Prensa.
Filloy, E. and Hoyos, V. (1993). A theory of the production of mathematical sign systems -the
case of algebraic representation of basic geometrical variation notions -, en Joanne, R
and Barbara, J. (eds.), Proceedings of Fifteenth Annual Meeting, North American
Chapter of the International Group for the Psychology of Mathematics Education, Vol.
1, pp. 135-141. Pacific Grove, CA, USA.
Filloy, E. and Hoyos, V., (en prensa, 1993). A theory of the production of mathematical sign systems the case of algebraic representation of basic geometrical variation notions.
27
Filloy, E. and Lema, S., 1985. Obstructions to Learn Elementary Geometrical Variation Concepts.
Thales’ Theorem, in K. Hart (ed.) Psychology of Mathematics Education Edition, Londres,
Inglaterra.
Filloy, E. and Lema, S. (1985). Obstructions to learn elementary geometrical variation
concepts. Thales’ Theorem, capítulo del libro no publicado, en K. Hart (ed.). Ratio and
Proportion.
Filloy, E; S, Lema. 1996. El Teorema de Thales: significado y sentido en un sistema matemático de
signos. En Investigaciones en Matemática Educativa. México, Grupo Editorial Iberoamérica, pp
55 - 75.
Filloy, E. y Rojano, T. (1984) La aparición del lenguaje aritmético--algebraico. L'Educazione
Matemática Año 5, No. 3, pp. 278-306, Cagliari, Italia.
Filloy, E and Rojano, T. (1984). From an arithmetical to an algebraic thought (a clinical study
with 12-13 year olds), en J. Moser (ed.), Proceedings of the Sixth Annual Meeting for
the Psychology of Mathematics Education, North American Chapter, pp. 51-56.
Madison, Wisconsin, USA.
Filloy, E.; Rojano, T. Movimiento de la incógnita, ¿terminación de la aritmética? México, 1983,
SME. por aparecer
Filloy, E and Rojano, T. (1985a). Obstructions to the acquisition of elemental algebraic
concepts and teaching strategies, en L. Streefland (ed.), Proceedings of the Ninth Annual
International Conference for the Psychology of Mathematics Education, pp. 154 -158.
Utrecht, Holland.
Filloy, E and Rojano, T. (1985b). Operating the unknown and models of teaching (a clinical
study 12-13 year olds with a high proficiency in pre-algebra), en S. Damarin y M.
Shelton (eds.), Proceedings of the Seventh Annual Meeting for the Psychology of
Mathematics Education, North American Chapter, pp. 75-79. Columbus, Ohio, USA.
Filloy, E and Rojano, T., 1984. From an Arithmetical to an Algebraic Thought (A clinical study with
12-13 year olds), in (ed.) Proceedings of the Sixth Annual Meeting for the Psychology of
Mathematics Education, North American Chapter. pp. 51-56. Madison, Wisconsin, USA.
Filloy, E. and Rojano, T., 1985a. Obstructions to the Acquisition of Elemental Algebraic Concepts and
Teaching Strategies, in (ed.) Proceedings of the Ninth Annual Conference for the Psychology of
Mathematics Education. pp. 154-158. Utrech, Holanda.
Filloy, E and Rojano, T., 1985b. Operating the Unknown and Models of Teaching (A clinical Study
with 12-13 year olds with a high proficiency in Pre-Algebra), in (ed.) Proceedings of the Sixth
Annual Meeting for the Psychology of Mathematics Education, North American Chapter. pp.
75-79. Ohio, USA.
Filloy, E and Rojano, T., 1989. Solving equations: the transition from Arithmetic to Algebra, For the
Learning of Mathematics, Vol. 9, Num. 2, pp. 19-25.
Filloy, E. and Rojano, T., 1991. Translating from Natural Language to the Mathematical System of
Algebraic Signs and viceversa (a clinical study with children in the pre-algebraic stage), in (ed.)
Proceedings of the Thirteenth Annual Meeting for the Psychology of Mathematics Education,
North American Chapter,. Vol. 1, pp. 29-35. Virginia, USA.
Filloy, E. and Rojano, T. (1989). Solving equations: the transition from arithmetic to algebra.
For the Learning of Mathematics, Vol. 9, No. 2, pp. 19-25.
28
Filloy, E. and Rojano T. La Aparición del lenguaje Aritmético-Algebraico. L’Educazione Matematica,
anno V. (3), Cagliari, Italia, 1984, pp. 278-306.
Filloy E. and Rojano T. From an Arithmetical to an Algebraic Thought (A clinical study with 12-13
years old). Proceedings of the Sixth Annual Conference of the International Group for the
Psychology of Mathematics Education, North American Chapter. Madison, Wisconsin, 1984,
pp. 51-56.
Filloy E. and Rojano T. Obstructions to the Acquisition of Elemental Albrebraic Concepts and
Teaching Strategies. Proceedings of the Nineth Conference for the Psychology of Mathematics,
International Group. Noordwikjerhout, The Netherlands, 1985.
Filloy E. and Rojano T. Operating the Unknown and Models of Teaching ( A clinical study among
children 12-13 with high proficiency in Pre-algebra). Proceedings of the Seventh Conference
for the Psychology of Mathematics, North America Chapter. Colombus, Ohio, 1985, pp. 75-79.
Filloy, E. and Rojano, T. (1991). Translating from natural language to the mathematical system
of algebraic signs and viceversa (a clinical study with children in the pre-algebraic
stage), en R.G. Underhill (ed.), Proceedings of the Thirteenth Annual Meeting for the
Psychology of Mathematics Education, North American Chapter, Vol. 1, pp 29 -35.
Blacksburg, VA, USA.
Filloy, E. and Rubio, G., (en prensa, 1993a). Family of arithmetic & algebra word problems and the
tensions between the different uses of algebraic expressions.
Filloy, E. and Rubio, G., (en prensa, 1993b). Didactic models, cognition and competence in the
solution of arithmetic & algebra word problems.
Filloy, E. and Rubio, G. (1993a). Family of arithmetic & algebra word problems and the
tensions between the different uses of algebraic expressions, en Joanne, R. y Barbara, J.
(eds.). Proceedings of Fifteenth Annual Meeting, North American Chapter of the
International Group for the Psychology of Mathematics Education, Vol. 1, pp. 142 -148.
Pacific Grove, CA, USA.
Filloy, E. and Rubio, G.: 1993, Family of Arithmetical and Algebraic Word Problems, and the
Tensions Between the Different Uses of Algebraic Expressions, Proceedings of the XV Annual
Meeting of International Group for the Psychology of Mathematics Education. North American
Chapter. Vol. I, pp. 1-142 to 1-150.
Filloy, E. and Rubio, G. (1993b). Didactic models, cognition and competence in the solution of
arithmetic & algebra word problems, en Ichiei, H.; Keiichi, S. y Fou -Lai, L. (eds.),
Proceedings of the Seventeenth International Conference for the Psychology of
Mathematics Education, Vol. 1, pp. 154-161. Tsukuba, Ibaraki, Japan.
Filloy E.; Rosshandler, R. And Trujillo, M. Reporte Parcial del Proyecto Adquisición del Lenguaje
Algebraico: Diagnóstico sobre Pre-Algebra, 82/83. Sección de Matemática Educativa,
Cinvestav del IPN, 1985.
Figueras, O.; Filloy, E. and Valdemoros, M. (1986). Some considerations on the graphic
representations of fractions and their interpretation, in G. Lappan and R. Even (eds.),
Proceedings of the Eighth Annual Meeting for the Psychology of Mathematics
Education, North American Chapter, pp. 78-83. East Lansing: Michigan, EE.UU.
Figueras, O.; Filloy, E. and Valdemoros, M. (1987). Some difficulties which obscure the
appropriations of the fraction concept, in J. Bergeron, N. Hercovics and C. Kieran (eds.),
29
Proceedings of the Eleventh Annual Meeting for the Psychology of Mathematics
Education, Vol. 1, pp. 366-372. Montreal, Canada.
Figueras, O., Filloy, E. and Valdemoros, M., 1986. Some considerations on the graphic representations
of fractions and their interpretation, in G. Lappan and E. Ruhama (eds.) Proceedings of the
Eight Annual Meeting for the Psychology of Mathematics Education, North American Chapter.
pp. 78-83. East Lansing, Michigan, USA.
Figueras, O., Filloy, E. and Valdemoros, M., 1987. Some difficulties which obscure the appropiation of
the fraction concept, in J. Bergeron, N. Hercovics and C. Kieran (eds.) Proceedings of the
Eleventh Annual Conference for the Psychology of Mathematics Education.. pp. 366-372.
Montreal, Canadá.
(Francesca, Piero della) Arrighi, G. Trattato D’Abbaco. Domus Galileana, Pisa, 1970.
Franci. R.; Rigatelli, L.; Toti. Storia della teoria delle equazioni algebraiche. Stumenti por una nuova
cultura. (Guide e manuali 40). Mursia Editore, Milano, 1979.
Freudenthal, H. 1983. Didactical phenomenology of mathematical structures. Reidel Publishing
Company, Dordrecht/Boston/Lancaster.
Gallardo, A. and Rojano, T. (1987). Common difficulties in the learning of algebra among
children displaying low and medium pre-algebraic proficiency levels, en Bergeron, J. C.;
Herscovics, N. y Kieran, C. (eds.), Vol. 1, pp. 301-307.
Hughes, B. Jordanus de Nemore, De Numeris Datis (A critical edition and traslation). University
of California Press. Berkeley, Los Angeles and London, 1981.
Kieran, C. The Interpretation of the Equal Sign: Symbol for an Equivalence Relation vs. An Operator
Symbol. An R. Karplus (ed.), Proceedings of the Fourth Conference of the International Group
for the Psychology of Mathematics Education. Berkeley, California, University of California,
1980, pp. 163-169.
Kieran, C. Concepts Associated with the Equality Symbols. Educational Studies in Mathematics, 12,
1981, pp. 317-320.
Kieran, C. y Filloy, E., 1989, El aprendizaje del álgebra escolar desde una perspectiva psicológica,
Enseñanza de las ciencias, Vol. 7, pp. 229-240.
Klein, J. Greek Mathematical Thought and the Origin of Algebra. The M.I.T. Press. Massachusetts
Institute of Technology, 1968.
Kuhn, T. S. (1962). The structure of scientific revolution. (University of Chicago Press:
Chicago) [Trad. castellana: La estructura de las revoluciones científicas (Fondo de
Cultura Económica: México, 1971).].
Matz, M. Towards a Process Model for High School Algebra Errors. Intelligent Tutoring Systems. D.
Seeman and J.S. Brown, Academic Press, 1982, pp. 25-50.
Mazzinghi, M° Antonio De’. Trattato di Fioretti (nella trascelta a cura di M°Benedetto, secondo la
lezione del Codice L.,IV,21, (Sec.XV) della Biblioteca degl’Intronati di Siena, e con
introduzione di Gino Arrighi). Domus Galileana Pisa, 1967.
McClenon, R. B. (1919). Leonardo de Pisa and his Liber Quadratorum. The American Mathematical
Monthly No. 1, Vol. XXVI, January, 1919.
Mélich, J-C. 1994. Del extraño al cómplice. La educación en la vida cotidiana. Barcelona. Anthropos.
30
Ore, O. (1988). Number Theory and Its History. Dover.
Peirce, Ch. S. 1987. Obra Lógico Semiótica. Madrd. Taurus.
Picutti, E. <<Flos>> di Leonardo Pisano. Codice E. 75 P. sup. della Biblioteca Ambrosiana di
Milano.
Puig, L. 1994. Semiótica y Matemáticas. Valencia: Eutopías, col Episteme.
Puig, L. 1997. Notes on Semiotics and Mathematics Education. Presentado en el grupo de semiótica de
las matemáticas en 21st Conference of PME. Finland 1997.
Puig, L. (1991). El De Numeris Datis de Jordanus de Nemore: esbozo de un análisis, en T.
Rojano, E. Filloy y L. Puig (eds.), Historia de las ideas algebraicas. Memorias del tercer
Simposio Internacional sobre Investigación en Educación Matemática, pp. 17 -26.
Valencia, España.
Puig, L. (1994). Semiótica y matemáticas. Eutopías 2a. época. Centro de Semiótica y teoría del
espectáculo de la Universitat de València & Asociación Vasca de Semiótica, Vol. 51.
Puig, L., 1991, El De Numeris Datis de Jordanus de Nemore: esbozo de un análisis, en T. Rojano, E.
Filloy y L. Puig (eds.) Historia de las ideas algebraicas. Memorias del Tercer Simposio
Internacional sobre Investigación en Educación Matemática, pp. 171-206.
Puig, L.: 1994, Semiótica y matemáticas. Valencia: Episteme, col. Eutopías.
Puig, L.: 1997a, Notes on Semiotics and Mathematics Education. Paper presented to the PME
Discussion Group “Semiotics Theory and Practice in Mathematics Education” (website:
htttp://www. scism.sbu.ac.uk/~pme/lp.html) at the 21st Conference of PME, Lathi, Finland.
Puig, L.: 1997b, Análisis fenomenológico, in Rico, ed. La educación matemática en la enseñanza
secundaria. Barcelona: ICE/Horsori.
Rojano, T. y Sutherland, R., 1991, La sintaxis algebraica en el proyecto viético, en T. Rojano, E. Filloy
y L. Puig (eds.) Historia de las ideas algebraicas. Memorias del Tercer Simposio Internacional
sobre Investigación en Educación Matemática, pp. 117-130.
Rojano, T. y Sutherland, R. (1991). La sintaxis algebraica en el proyecto viético, en T. Rojano,
E. Filloy y L. Puig. (eds.), Historia de las ideas algebraicas. Memorias del tercer
Simposio Internacional sobre Investigación en Educación Matemática, pp. 117-130.
Valencia, España.
Rojano, T. De la Artitmética al Algebra (estudio clínico con niños de 12 a 13 años de edad). Doctoral
Dissertation. Centro de Investigación y de Estudios Avanzados del IPN., 1985, México.
Rojano, T. Learning and Usage of Algebraic Syntax: Its Semantic Aspects. Proceedings of the Eightgh
Annual Meeting for the Psychology of Mathematics, North American Chapter. East Lansing,
Michigan, 1986, pp. 121-126.
Springer Series in Cognitive Development.
Springer Series in Language and Communication.
Sigler, L. E. (1987). Leonardo Pisano Fibonacci: The Book of Squares. Academic Press, Inc.
Schütz, A. 1993. La construcción significativa del mundo social. Introducción a la sociología
comprensiva. España. Paidós.
31
Talens, J. & Company, J.M. 1984. The Textual Space: On the Notion of Text. The Journal of Midwest
Modern Language Association, vol 17, pp 24 - 76.
Ver Eecke, P. (1952). Léonard de Pise. Desclée de Brouwer.
Ver Eecke, P. (1973). Leonardo de Pisa: El Libro de los Números Cuadrados. Editorial Universitaria
de Buenos Aires, Argentina.
(Viète, F.) Witmer, T.R. (tr.) The Analytical Art. The Kent State University Press, U.S., 1981.
Weil, A. (1984). Number Theory: An approach through history. From Hammurapi to Legendre.
BIRKHÄUSER.
Wittgenstein, L.: 1956, Remarks on the Foundations of Mathematics. Edited by G. H. von Wright, R.
Rhees, and G. E. M. Anscombe. Oxford: Basil Blackwell.
Wittgenstein, L. (1994). Remarks on the foundations of mathematics, edición d e von Wright,
Rhees and Anscombe (Blackwell: Oxford). Trad. castellana: 1987, Observaciones sobre
los fundamentos de las matemáticas (Alianza: Madrid).
32