GEOMETRÍA DE MASAS

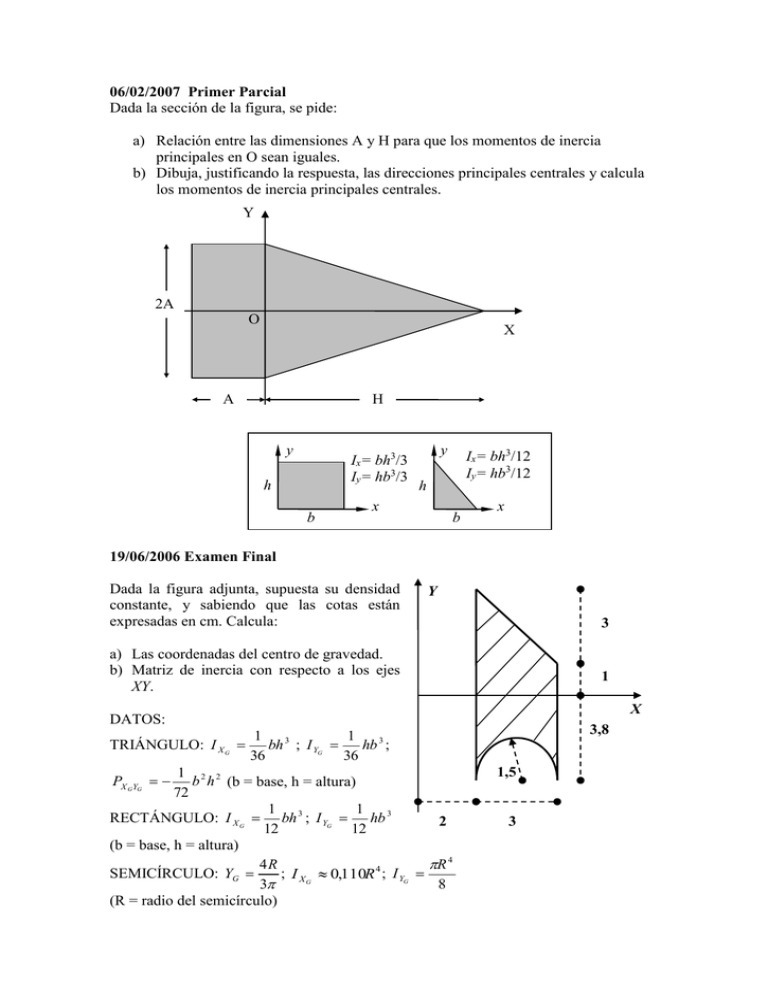
06/02/2007 Primer Parcial
Dada la sección de la figura, se pide:
a) Relación entre las dimensiones A y H para que los momentos de inercia
principales en O sean iguales.
b) Dibuja, justificando la respuesta, las direcciones principales centrales y calcula
los momentos de inercia principales centrales.
Y
2A
O
X
A
H
y
Ix= bh3/3
Iy= hb3/3
h
b
y
Ix= bh3/12
Iy= hb3/12
h
x
b
x
19/06/2006 Examen Final
Dada la figura adjunta, supuesta su densidad
constante, y sabiendo que las cotas están
expresadas en cm. Calcula:
Y
3
a) Las coordenadas del centro de gravedad.
b) Matriz de inercia con respecto a los ejes
XY.
1
X
DATOS:
TRIÁNGULO: I X G 
1 2 2
b h (b = base, h = altura)
72
1
1
RECTÁNGULO: I X G  bh 3 ; I YG  hb 3
2
12
12
(b = base, h = altura)
4R
R 4
SEMICÍRCULO: YG 
; I X G  0,110R 4 ; I YG 
3
8
(R = radio del semicírculo)
PX GYG  
3,8
1
1
bh 3 ; I YG 
hb 3 ;
36
36
1,5
3
11/09/2007 Examen Septiembre
La placa de la figura está hecha de acero de 1 mm de espesor. Está sustentada por un
pasador en C y un cable en B. Se pide:
a) Centro de gravedad de la placa.
b) Reacción en el soporte C y tensión en el cable.
c) Momentos de inercia respecto del sistema de ejes coordenados GXGYG.
Densidad del acero: 7800 kg/m3
12 cm
18 cm
6 cm
Y
8 cm
C
16 cm
T
B
45º
12 cm
8 cm
X
O
4 cm
14/06/2007 Examen Final
a) Calcule los momentos y direcciones
principales centrales de la sección
transversal de la columna que muestra
la figura.
200
100
b) Calcule los radios de giro de la sección
respecto a sus ejes de simetría.
200
NOTA: Las cotas de la figura están dadas
en mm.
200 80 200
YG
XG
h
b
1 3
bh
12
1
 hb 3
12
I XG 
I YG
26/11/2005 Examen Diciembre
Dado un rombo homogéneo cuyas diagonales valen 4 y 6 cm tal y como se indica,
calcula:
Y
a) La matriz central de inercia, referida a los ejes OXY
de la figura
b) La matriz de inercia en el punto A. Dibuja asimismo
los ejes principales de inercia en el punto A.
c) En el rombo anterior, calcula la posición del centro
de gravedad si quitamos el triángulo superior
izquierdo.
y
6 cm
A
O
X
Ix= bh3/12
Iy= hb3/12
h
b
x
4 cm
09/12/2003 Examen Diciembre
La sección transversal de una viga es la que se muestra en la figura. Determina los
momentos de inercia y el producto de inercia respecto a los ejes coordenados que pasan
por el centro de gravedad. Suponga que se quiere reducir Ix en un 20% colocando un
agujero circular con su centro en el centro de gravedad de la sección, ¿cuál debe ser el
radio del agujero? Dibuja los ejes principales en el punto A explicando sus propiedades
correctamente.
En los recuadros de la izquierda están las expresiones y datos para aplicar al ejercicio.
3m
y
b
3m
A
h
R
G
G
a
6m
x
2m
2m
(a  2 b ) h
yG 
3(a  b)
I xG  I yG
R 4

4
I xG 
(a 2  4ab  b 2 )h 3
36(a  b)
I yG 
1  3 (a  b) (a  b) 2  2(2a  b) 2
a 
12 
12

h

04/02/21004 Primer Parcial
Dada la sección transversal de la figura, determina los momentos de inercia respecto de
unos ejes que pasen por el centro de gravedad y que sean paralelos a los ejes OXY.
Determina las direcciones principales centrales. Justifica correctamente la solución
dada.
En los recuadros de la izquierda están las expresiones y datos para aplicar al ejercicio.
Y
1m
G
h
R
1m
5m
G
b
bh
12
b3  h

12
3
I xG 
I yG
4R
3 
 8 
     R4
 8 9 
yG 
I xG
I yG
O
R 4

8
X
2m
y
14/12/2004 Examen Diciembre
La sección de una estructura es la que se muestra
en la figura. Se pretende conseguir que los
momentos de inercia tengan un valor de 332 m4.
Se pide:
a) El radio del hueco circular.
b) Direcciones principales en O, razonando
correctamente la respuesta.
c) Matriz de inercia en O’.
d) Momentos de inercia y direcciones
principales centrales.
6m
O’
6m
Y
R
h
G
O
I x  I y  I yG 
  R4
4
b
1
 b  h3
3
1
  b  h3
12
X
1 3
b h
3
1
  b3  h
12
Ix 
Iy 
I xG
I yG
x
01/02/2005 Primer Parcial
Si en el cuadrado de la figura de 2 m de lado se realiza un hueco
triangular como el representado, ¿cuál debe ser la altura de dicho
hueco, para que el momento de inercia respecto del eje Y disminuya en
un 25%? Dibújense los ejes principales centrales conocida la altura del
triángulo.
y
x
y
h
Y
b
1
I x   b  h3
12
1
I y   b3  h
12
1 2 2
Pxy 
b h
24
x
1000 kN/m
1
I xG 
 b  h3
36
1 3
I yG 
b h
36
1 2 2
PxG yG 
b h
72
Y
h
O
b
X
1
1
I x   b  h3
I xG   b  h 3
3
12
1
1
I y   b3  h
I yG   b 3  h
3
12
1
Pxy   b 2  h 2
4
12/09/2005 Examen Septiembre
a
Dada la sección homogénea de un perfil
simétrico en L, de anchura a, calcula la longitud
máxima de la aleta x, para que la posición del
c.d.g. de la sección se encuentre dentro de la
sección.
X
x
26/11/2005 Primer Parcial
A un disco homogéneo de radio R= 8 cm se le
realiza un taladro de diámetro  = 4 cm tal y
como se indica en la figura. Calcula:
a) Matriz de inercia en el origen.
b) Matriz de inercia en el centro de gravedad.
c) Valores máximo y mínimo de los momentos
de inercia centrales así como la dirección de
los ejes principales centrales.
4
8
2
yG
IxG=IyG=πR4/4
R
G
y
xG
2
x
02/02/2003 Primer Parcial
Dada la sección de la viga de la figura, dibújense los ejes principales centrales de la
misma, razonando correctamente la respuesta. Calcúlese el momento de inercia respecto
del eje X de la sección.
1
Ix   b  h3;
3
1
Ix G   b  h3
12
3 cm
3 cm
2 cm
2 cm
6 cm
2 cm
6 cm
6 cm
x
02/07/2004 Examen Final
Determina los elementos principales centrales de inercia de la sección simétrica del
ángulo de la figura, y dibuja los ejes correspondientes.
1
1
(Rectángulo: I XG  b h 3 ; I YG  b 3 h )
12
12
140 mm
10 mm
siendo b la base y h la altura.
140 mm
ÑÑÑÑÑÑÑÑÑÑÑ
10 mm