guiaestudio2 parcial1 fxvectoriales fxvariasvariables calculo2 1612 v1

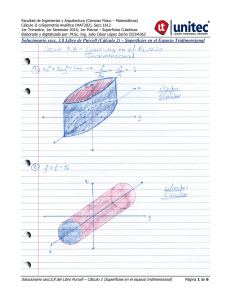
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
2da Guía de Estudio del 1er Parcial
Funciones Vectoriales
Modelación de Movimiento de Proyectiles
Superficies en el Espacio Tridimensional
Coordenadas Cilíndricas y Esféricas
Límites de Funciones en Varias Variables
Derivadas Parciales – Conceptos Básicos
Guía Complementaria No.02 – v 3.0
Comentarios Generales
Ésta guía cumple única y exclusivamente la función de repaso o complemento de los temas que posiblemente
serán evaluados en el primer examen parcial, además, se establece que en ningún momento ésta guía de estudio
pretende reemplazar el libro de texto y mucho menos, proporcionar un formato de los ejercicios que podrían ser
evaluados en un examen; se hace ésta aclaración para evitar especulaciones y conjeturas erróneas entre los
estudiantes de ésta y las otras secciones de Cálculo II, dado que ésta herramienta ha sido elaborada tomando
como referencia diferentes libros de Cálculo en varias variables y guías de universidades extranjeras, que a
criterio del Catedrático, genera un valor agregado en el conocimiento de los futuros profesionales de la
ingeniería.
Se le recuerda la importancia de trabajar con disciplina, perseverancia y honestidad cada ejercicio, dado que Ud.
es el único responsable de su éxito o fracaso, el catedrático no es más que un facilitador del conocimiento, por lo
tanto, ante cualquier inquietud no dude en consultarlo.
Instrucciones Específicas de Entrega:
Para que el trabajo grupal sea aceptado y revisado por la totalidad del puntaje, el documento deberá
cumplir las siguientes condiciones:
a) Desarrollo en hojas blancas o rayadas (sin espiral) tamaño carta utilizando ambas caras de la hoja y
como mínimo grapada.
b) Formato de presentación conforme a lo estipulado en el silabo de curso (portada y todos los demás
elementos que apliquen según sea el caso).
c) Los ejercicios deberán estar listados en el orden numérico correlativo de la guía.
d) Todas las páginas que conformen el trabajo (excepto la portada) deberán estar etiquetadas con su
respectivo número de página en la esquina inferior derecha de las mismas y el formato será:
“X de Y”, donde: X = página cualquiera; Y = número total de páginas que forman el trabajo.
e) Ser entregado en la fecha estipulada en el calendario del aula virtual.
A.-) En los problemas del No.01 – No.08, dada la función vectorial de desplazamiento, determine la
distancia recorrida por la partícula en el intervalo de tiempo establecido.
1) r t   t i  4t j  3t k
0  t 1
R/=
2) r t   i  t
2
3
jt k
26
0t2
R/=
Repaso General de Funciones Vectoriales y Funciones en Varias Variables

1
80 10  8
27

Página 1 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
3)
0  t  3
4t ,  cos t , sen t 
2
R/=
4)
2 sen t , 5t , 2 cos t 
3
17
2
0t 
R/=  29
5) r t   a cos t  i  asen t  j  bt k
0  t  2
a, b ctes
R/= 2 a 2  b 2
6)
0t 
cos t   tsen t , sen t   t cos t , t 2
2
R/=
3
7) r t   t i  4 t 2 j  1 t 2 k
3
2
0t2
R/= 2 13 
8) r t   t  cos t  i  t  sen t  j 
2 5
8
2 t k


3
3
ln 4  13  1  ln3   4.816
2
2
0t2
R/=
7


 
3
3
ln 2  7  ln 3  4.126
2
2
C.-) En los problemas del No.09 – No.11, dada la función vectorial de desplazamiento, determine las
características físicas y vectores especiales solicitados
9) Dada r t   7 sen 3t  i  7 cos 3t  j  14t k ;
10) Dada r t   t
2
4
i  2 cos t  j  2 sen t  k ;
t   , determine  t , T t , N t , B t  .
3
t1   , determine  t , T t , N t , B t  .
11) Dada r t   6 sen 2t  i  6 cos 2t  j  5t  k , determine  t  .
B.-) En los problemas del No.12 – No.17, utilice el método de modelo a través de proyectiles para
resolver las preguntas planteadas.
12) Determinar la altura máxima y el alcance de un proyectil disparado desde una altura de 3 pies
sobre el nivel del suelo con V0 de 900 pies/s y con ángulo de 45° sobre la horizontal.
R/=> altura máxima= 6,331.13 pies
Alcance= 25,315.50 pies
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 2 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
13) Un jugador de béisbol en segunda base lanza una pelota al jugador de primera base a 90 pies, la
pelota es lanzada desde 5 pies sobre el nivel del suelo con una V0 de 50mi/hr y con un ángulo
de 15° con la horizontal. ¿A qué altura cacha la pelota el jugador de primera base?
R=> 3.286 pies
14) El mariscal de campo de un equipo de futbol americano lanza un pase a una altura de 7 pies
sobre el campo de juego y el balón de futbol lo captura un receptor a 30 yardas a una altura de 4
pies sobre el nivel del suelo. El pase se lanza con un ángulo de 35° con respecto a la horizontal.
a.-) hallar la rapidez del balón de futbol al ser lanzado.
b.-) hallar la altura máxima del balón de futbol.
c.-) hallar el tiempo que el receptor tiene para alcanzar la posición apropiada después de
que el mariscal de campo lanza el balón de futbol.
R=> a) 54.09 pies/s
b) 22 pies & c) 2 segundos
15) Un bombardero vuela horizontalmente a una altitud de 3,200 pies con una velocidad de 400
pies/s cuando suelta una bomba. Un proyectil se lanza 5 segundos después desde un cañón
orientado hacia el bombardero y abajo a 5,000 pies del punto original del bombardero, como se
muestra en la figura. El proyectil va a interceptar la bomba a una altitud de 1,600 pies.
Determinar la velocidad inicial y el ángulo de inclinación del proyectil. (Despreciar la
resistencia del aire.)
R=>V0=447.2 pies/s
Angulo=63.43°
Fuente: Cálculo 2 de varias variables, 9ª edición, Ron Larson y Bruce Edwards (pag.883)
16) Un bombardero vuela a una altitud de
30,000 pies a una velocidad de 540 millas
por hora (ver figura). ¿Cuándo debe lanzar
la bomba para que impacte en el blanco?
(Dar la respuesta en términos del ángulo de
depresión del avión con respecto a la
horizontal.), ¿Cuál es la velocidad de la
bomba en el momento del impacto?
∝
∝
R/=>1,596 pies/s; ángulo de 41.18°
(Sugerencia: utilice como referencia el triángulo rectángulo pintado en rojo)
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 3 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
17) Una pelota de béisbol es golpeada 3 pies sobre el nivel del suelo, se aleja del bate con un ángulo
de 45° y es cachada por un jardinero a tres pies sobre el nivel del suelo y a 300 pies del plato de
lanzamiento. ¿Cuál es la rapidez inicial de la pelota y que altura alcanza?
R=> rapidez inicial= 95.98 pies/s
Altura máxima= 78 pies
18) Un proyectil se lanza desde el borde de un
acantilado de 150m con una velocidad inicial
de 180 m/s a un ángulo de 30° con la
horizontal. Si se ignora la resistencia del aire,
encuentre:
a) la distancia horizontal desde el cañón hasta el
punto donde el proyectil golpea el suelo,
b) la elevación máxima sobre el suelo que
alcanza el proyectil.
19) Un proyectil se lanza con una
velocidad inicial de 800 ft/s a un
blanco ubicado a 2000 ft por arriba
del cañón A y a una distancia
horizontal de 12,000 ft. Si se
ignora la resistencia del aire,
determine el valor del ángulo de
disparo α.
20) Determine el ángulo θ más
pequeño, medido desde la
horizontal, con el cual la
manguera debe ser dirigida de
manera que la corriente de agua
toque el fondo de la pared en el
punto B. La rapidez del agua en
la tobera es VC = 48 pies/s.
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 4 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
21) Una pelota de golf es golpeada con
velocidad de 80 pies/seg. como se
muestra. Determine la distancia d a la
que llegará.
22) Una pelota de béisbol, bateada por un
jugador de los Medias Rojas de Boston
con un angulo de 20° a 3 pies sobre el
suelo, pasó sobre el extremo izquierdo del
“Monstruo Verde”, como se le conoce a la
pared del jardín izquierdo en el estadio
Fenway Park. Esta pared tiene 37 pies de
altura y está a 315 pies del home (ver
figura adjunta).
a) ¿Cuál fue la rapidez inicial de la
pelota?
b) ¿Cuánto tiempo tardó la pelota en
llegar a la pared?
23) Una pelota de golf es
golpeada con una rapidez
inicial de 116 pies/s con un
ángulo de elevación de 45°
desde el tee hasta un Green
que tiene una altura de 45 pies
sobre el tee, como se muestra
en el diagrama. Si el pin, a
369 pies de distancia
horizontal, no estorba,
¿Dónde caerá la pelota en
relación con el pin?
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 5 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
C.-) En los problemas del No.24 – No.32, indique el nombre de la ecuación en función de las
características calculadas, sus trazas en los planos (xy, xz, yz) y bosqueje de forma aproximada dicha
función en el espacio tridimensional.
2
2
2
24) 4 x  y  z  8 x  2 y  2 z  3  0
25) x 2  y 2  z 2  8  8 y  6 z  24  0
26) x 2  2 y 2  4 z 2  8
2
2
2
27) x  y  z  10 z  25  0
28) x 2  4 y 2  4 z 2  6 x  16 y  16 z  5  0
29) x 2  2 y 2  z 2  4 x  4 y  2 z  3  0
30) 4 x 2  y 2  z 2  8 x  0
31) 16 x 2  9 y 2  16 z 2  32 x  36 y  36  0
2
2
2
32) 9 x  y  9 z  54 x  4 y  54 z  4  0
Respuestas Sugeridas
24.-) hiperboloide de una hoja con centro en (1,1,-1)
25.-) Esfera
26.-) Cono elíptico
27.-) Cono elíptico
28.-) Hiperboloide de una hoja
29.-) Elipsoide
30.-) Elipsoide
31.-) Elipsoide con centro en (1,2,0)
32.-) Cono elíptico con centro en (3,2,-3)
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 6 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
Gráficas sugeridas de las respuestas pertenecientes a las funciones cuádricas de los ejercicios 15–23.
24.)
25.-)
26.-)
27.-)
28.-)
29.-)
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 7 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
30.-)
31.-)
32-)
D.-) En los problemas del No.33–No.37, hallar una ecuación en coordenadas cilíndricas de la
ecuación dada en rectangulares, e intente nombrar la superficie determinada.
33) z  4
34) x  9
36) z  x 2  y 2  11
35) x 2  y 2  z 2  17
37) x 2  y 2  z 2  3 z  0
E.-) En los problemas del No.38–No.42, hallar una ecuación en coordenadas rectangulares de la
ecuación dada en cilíndricas, e intente nombrar la superficie determinada.
38) r  3
39) z  2
40)   
41) z  r cos  
42) r  2 cos  
2
2
6
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 8 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
F.-) En los problemas del No.43 – No.47, hallar una ecuación en coordenadas esféricas de la
ecuación dada en rectangulares, e intente nombrar la superficie determinada.
43) y  2
44) x 2  y 2  z 2  49
45) x 2  y 2  3 z 2  0
46) x 2  y 2  2z 2
47) x 2  y 2  z 2  9 z  0
G.-) En los problemas del No.48–No.52, hallar una ecuación en coordenadas rectangulares de la
ecuación dada en esféricas, e intente nombrar la superficie determinada.
 5
49)   3
4
48)
50)   
51)
52)
  2 sec  
  4 csc   sec  
2
H.-) En el Ejercicio No.53 y 54, asocie la ecuación (dada en coordenadas cilíndricas o esféricas),
con su respectiva gráfica.
53.1.-) r  5
53.2.-)   
4
53.3.-)   5
53.4.-)   
4
53.5.-) r 2  z
53.6.-)   4 sec  
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 9 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
54 Asocie la ecuación con su respectiva gráfica completando el cuadro mostrados al costado
derecho.
Ecuación
54.1.-)
Inciso
x 2 y 2 z2


1
9
16
9
54.2.-) 15 x 2  4 y 2  15 z 2  4
54.3.-) 4 x 2  y 2  4 z 2  4
54.4.-) y 2  4 x 2  9z 2
54.5.-) 4 x 2  4 y  z 2  0
54.6.-) 4 x 2  y 2  4 z  0
Respuestas sugeridas para los ejercicios del No.27 al No.46
33. igual , z  4
34. r  9 sec  
2
35. r  z
36.
37.
38.
39.
40.
 17
z  r  11
r 2  z 2  3z  0
x2  y2  9
igual , z  2
x y 30
2
41. z  x
42.
2
2
x  12  y 2  1
  2 csc  csc  
 7
45.   
3
43.
44.
46. tan     2
47.   9 cos  
48.
49.
50.
51.
52.
x 2  y 2  z 2  25
x y0
z0
z2
x4
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 10 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
I.-) En los problemas del No.55 – No.61, realice un análisis del límite propuesto en función del
requerimiento y/o métodos recomendados para establecer su existencia o no existencia.
 x5 y 3  x3 y 5 

 a través de herramientas algebraicas.
55) Estudie
lim
 x , y  1,1  x 6 y 4  x 4 y 6 
-------------------------------------------------------------------------------------------------------------------------56) Estudie
 2x2  y4 

 en la trayectoria x = ky2 (k constante).
lim
2
4

 x , y  0,0   3 x  5 y 
-------------------------------------------------------------------------------------------------------------------------57) Estudie
 5 x3  7 y 3 
 en la trayectoria y = kx (k constante).

lim
 x , y  0,0   2 x 3  3 y 3 
-------------------------------------------------------------------------------------------------------------------------58) Estudie
 3 x  12 y 

 utilizando límites reiterados.
lim
 x , y  4,1  x 2  16 y 2 
--------------------------------------------------------------------------------------------------------------------------

 

 sen x 2  y 2 cos x 2  y 2 

 a través de coordenadas polares.
59) Estudie
lim
2
2


 x , y  0,0  
x y

--------------------------------------------------------------------------------------------------------------------------


x2 y2

 utilizando la trayectoria y = kx (k cte).
60) Estudie
lim
4
2
2

 x , y  0,0   2 x y   x  y  
-------------------------------------------------------------------------------------------------------------------------61) Estudie
 x2  y2  4 y  2x  5 

 utilizando la trayectoria y + 2 = m(x – 1).
lim
 x , y  1, 2   x 2  2 y 2  2 x  8 y  9 
J.-) En los problemas del No.62 – No.66, dada la función f(x,y), hallar las dos derivadas parciales de
primer orden (Fx & Fy).
 x2  4x  2 y 

62) f  x, y   ln 
 9 x 2  4 y 2  36 x 


63) f  x, y  
x2  y 2  4
2
2
2
64) 4 z  36 y  9 y  72 x  36 x  36
65) z  sen 5 x  cos 5 y 
x2  y 2
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 11 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363



   cos42 y 
 
66) w   ln y  csc z 2  y  arctan 3 z  csc log x e
K.-) En los problemas del No.67 – No.70, calcular las derivadas parciales de primer orden con
respecto a x, y & z
67) H  x, y , z   sen  x  2 y  3 z 
68) w 
69) w  ln 
x 2  y 2  z 2 


x2  y2  z2
70) G  x, y , z  
1
1  x2  y2  z2
L.-) En los problemas del No.71 – No.72, encontrar la primera derivada parcial con respecto a x.
 
2
2 z
71) f  x, y , z   tan y 2 z e z  y
y 
72) f  x, y , z   xsenh 

 z

z y 2  2 y 1

M.-) En los problemas del No.73 – No.76, hallar las primeras parciales de z ( z/ x & z/ y)
2
73) x  yz  z
2
75) z  e sen  y  z 
x
1
74) tan  x  y   tan  y  z   1
76) x ln  y   y z  z  8
2
2
N.-) En los problemas del No.77 – No.79, hallar las parciales de w ( w/ x, w/ y & w/ z)
77) xy  yz  wz  wx  5
2
2
2
2
78) x  y  z  5 yw  10 w  2
79) cos  xy   sen  yz   wz  20
O.-) En los problemas del No.80 – No.83, desarrolle las demostraciones solicitadas
80) En física se demuestra que la temperatura u(x, t) en el momento t en el punto x de un cilindro
largo y aislado, que se encuentre a lo largo del eje x, satisface la ecuación del calor
unidimensional:
u
 2u
 k 2 (donde k es una constante)
t
x
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 12 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
 n 2  k t
Demuestre que la función: u  u  x, t   e
 sen nx 
Satisface la ecuación del calor unidimensional para cualquier valor de la constante n.
-------------------------------------------------------------------------------------------------------------------------81) La ecuación del calor bidimensional para una placa delgada y aislada es:
  2u  2u 
u

 k 2 
2
 x
t
y 



 m 2  n 2  k t
Demuestre que la función: u  u  x, y , t   e
 sen mx   cos ny 
Satisface esta ecuación para cualquier valor de las constantes m y n.
-------------------------------------------------------------------------------------------------------------------------82) Una función de temperatura de estado estable u = u(x, y) para una placa delgada y plana
satisface la ecuación de Laplace.
 2u
 x2

 2u
 y2
0
Determine cuál de las funciones siguientes satisface la ecuación de Laplace:
a) u  ln 
x 2  y 2 


b) u 
c) u  arctan 
y 

 x
d) u  e  x  sen  y 
x2  y2
-------------------------------------------------------------------------------------------------------------------------83) Una cuerda se estira a lo largo del eje x, se fija en cada extremo y luego se sujeta a vibración.
En física se demuestra que el desplazamiento y = y(x, t) del punto de la cuerda ubicado en x en
el momento t, satisface la ecuación de onda unidimensional
2 y
 t2
a
2
2 y
 x2
Donde la constante a depende de la densidad y tensión de la cuerda. Demuestre que las
funciones siguientes satisfacen la ecuación de onda unidimensional:
a) y  sen  x  a  t 
b) y  cosh 3 x  a  t 
c) y  sen k  x  cos k  a  t  donde k es una constante.
-------------------------------------------------------------------------------------------------------------------------Bibliografía utilizada para la recopilación y elaboración de los ejercicios propuestos en ésta Guía.
1. Purcell, E. (2009). Cálculo 1, 1ª ed. México D.F, México. Pearson Educación.
2. Stewart, J. (2002). Cálculo, Trascendentes Tempranas, 4ª ed. México D.F, México. Thomson Editores.
3. Zill, D. (1994). Cálculo con Geometría Analítica, 1ª ed. México D.F, México. Grupo Editorial
Iberoamericana.
4. Stewart, J. (2008). Cálculo Varias Variables, Trascendentes Tempranas, 6ª ed. México D.F, México.
Cengage Learning Editores.
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 13 de 14
Facultad de Ingenierías y Arquitectura (Ciencias Físico – Matemáticas)
Cálculo II c/Geometría Analítica (MAT202), Secc.1612
1er Trimestre, 1er Semestre 2016; 1er Parcial – 2da Guía de Estudio
Recopilado y digitalizado por: M.Sc. Ing. Julio César López Zerón CICH4363
5. Stewart, J. (2012). Cálculo Varias Variables, Trascendentes Tempranas, 7ª ed. México D.F, México.
Cengage Learning Editores.
6. Edwards, H.; Penney, D. (2008). Cálculo con Trascendentes Tempranas, 7ª ed. México D.F, México.
Pearson Educación.
7. Thomas, G. (2010). Cálculo Varias Variables, 12ª ed. México D.F, México. Pearson Educación.
8. Zill, D. (2011). Cálculo Varias Variables. Trascendentes Tempranas, 4ª ed. México D.F, México. McGrawHill Educación.
9. Larson, R.; Edwards, B. (2010). Cálculo 2 de Varias Variables, 9ª ed. México D.F, México. McGraw-Hill
Educación.
10. Zill, D.; Wright, W. (2011). Matemáticas 3. Cálculo de Varias Variables. 1ª ed. México D.F, México.
McGraw-Hill Educación.
11. Juárez, I.; Moreno, J.; Tomeo, V. (2007). Cálculo en Varias Variables Paso a Paso. 1ª ed. Madrid, España.
Thomson Editores.
12. Cálculo Diferencial e Integral. Ingeniería Matemática; Facultad de Ciencias Físicas y Matemáticas.
Universidad de Chile. Santiago de Chile.
13. Carrasco, P.; Torres, G. (2008). Matemáticas IV – Cálculo Integral, 1ª ed. México. Cengage Learning
Editores.
14. Cortes, I. (1978). Cálculo Elemental. Universidad Nacional Experimental de Táchira. Táchira, República
Bolivariana de Venezuela.
15. Rojas, D. Matemáticas II: Ingeniería Mecánica y Química. Instituto Universitario de Tecnología “José
Antonio Anzoátegui”. República Bolivariana de Venezuela.
16. Universidad de Santiago de Chile, (2001-2010). Pruebas acumulativas y exámenes parciales Cálculo 10001.
Santiago de Chile, Chile.
17. Jiménez, B. Cruz, L. Meza, M. (2009). Elementos de Cálculo Integral. 1ª ed. Instituto Tecnológico y de
Estudios Superiores de Monterrey (ITESM). México. Limusa, Grupo Noriega Editores.
JUCELO1209® D.R.2016
Repaso General de Funciones Vectoriales y Funciones en Varias Variables
Página 14 de 14