Sistema Solar y propiedades: Ejemplo de Regresión Lineal

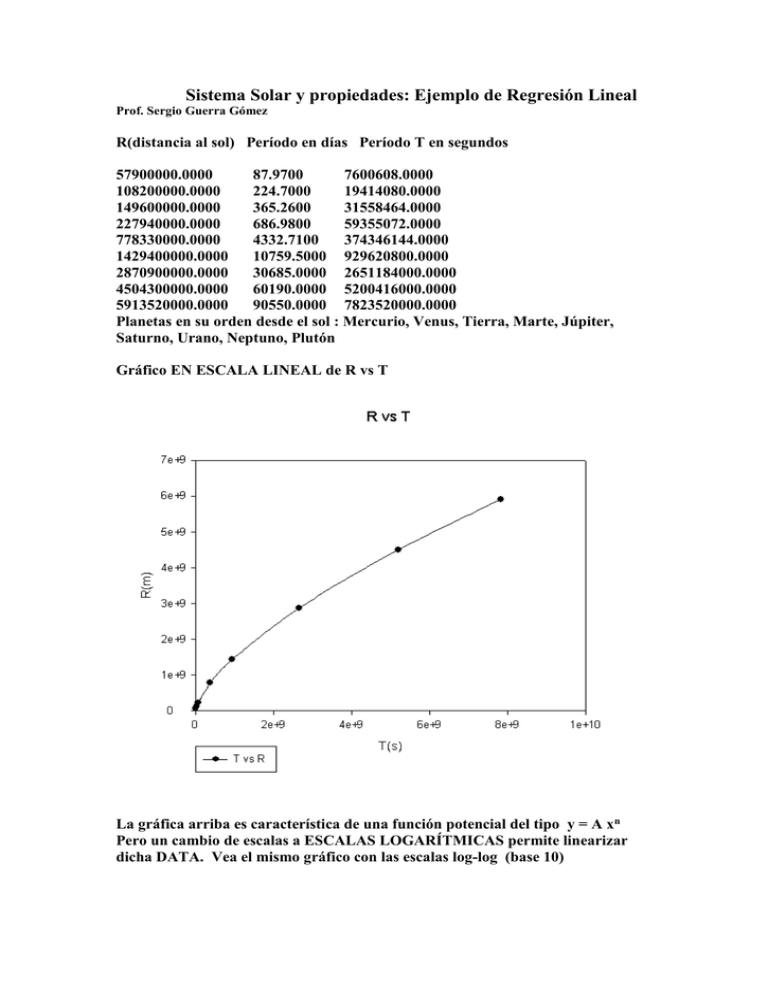
Sistema Solar y propiedades: Ejemplo de Regresión Lineal
Prof. Sergio Guerra Gómez
R(distancia al sol) Período en días Período T en segundos
57900000.0000
87.9700
7600608.0000
108200000.0000
224.7000
19414080.0000
149600000.0000
365.2600
31558464.0000
227940000.0000
686.9800
59355072.0000
778330000.0000
4332.7100
374346144.0000
1429400000.0000
10759.5000 929620800.0000
2870900000.0000
30685.0000 2651184000.0000
4504300000.0000
60190.0000 5200416000.0000
5913520000.0000
90550.0000 7823520000.0000
Planetas en su orden desde el sol : Mercurio, Venus, Tierra, Marte, Júpiter,
Saturno, Urano, Neptuno, Plutón
Gráfico EN ESCALA LINEAL de R vs T
La gráfica arriba es característica de una función potencial del tipo y = A xn
Pero un cambio de escalas a ESCALAS LOGARÍTMICAS permite linearizar
dicha DATA. Vea el mismo gráfico con las escalas log-log (base 10)
Como podemos ver el cambio de variables, aquí cambiar ambas escalas a escalas
logarítmicas logra LINEARIZAR la curva inicial. Y cuando tenemos una línea
recta (o próxima a ella) podemos usar un método de Regresión Lineal que nos
permite hacer el ajuste como ya hemos estudiado.
Vea el ajuste aquí abajo usando el programa Sigma Plot que usted conoce:
Coefficients:
b[0] 3.1735
b[1] 0.6669
r²
1.0000
Function Values:
x
f(x)
6.8808 7.7626
6.9411 7.8028
7.0014 7.8430
7.0616 7.8831
7.1219 7.9233
7.1821 7.9635
7.2424 8.0037
7.3026 8.0439
7.3629 8.0841
7.4231 8.1243
7.4834 8.1644
7.5436 8.2046
7.6039 8.2448
7.6641 8.2850
7.7244 8.3252
7.7846 8.3654
7.8449 8.4055
7.9051 8.4457
7.9654 8.4859
8.0256 8.5261
8.0859 8.5663
8.1461 8.6065
8.2064 8.6466
8.2666 8.6868
8.3269 8.7270
8.3871 8.7672
8.4474 8.8074
8.5076 8.8476
8.5679 8.8877
8.6281 8.9279
8.6884 8.9681
8.7486 9.0083
8.8089 9.0485
8.8691 9.0887
8.9294 9.1288
8.9896 9.1690
9.0499 9.2092
9.1101 9.2494
9.1704 9.2896
9.2306 9.3298
9.2909 9.3700
9.3511 9.4101
9.4114 9.4503
9.4716 9.4905
9.5319 9.5307
9.5921 9.5709
9.6524 9.6111
9.7126 9.6512
9.7729 9.6914
9.8332 9.7316
9.8934 9.7718
Si escribimos nuestra ecuación: R = A Tn
El valor de “n”nos lo da el coeficiente b[1] del ajuste es decir “n = 0,6669”
Y el “ log A” nos lo da el coeficiente b[0] es decir “logA = 3.1735”
O sea :
A = 103.1735 = 1491.1
Note el valor de R = 1.0000
muy bueno!!!!!!!