manejo de geoposicionador satelital de tipo navegador

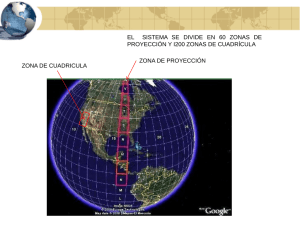
UNRC – AFIP – CURSO DE MANEJO MANEJO DE GEOPOSICIONADOR SATELITAL DE TIPO NAVEGADOR
MANEJO DE GEOPOSICIONADOR SATELITAL DE TIPO NAVEGADOR
APUNTES DE CLASE
CONTENIDOS:
SISTEMAS ESPACIALES DE REFERENCIA. LATITUD Y LONGITUD. SISTEMAS
DE PROYECCIÓN. SISTEMA TM Y UTM. CONVERSIÓN DE COORDENADAS.
OPERACIONES BÁSICAS CON UN RECEPTOR DE NAVEGACIÓN GPS.
ALMACENAMIENTO DE DATOS. TRANSFERENCIA DE DATOS A UNA PC.
SISTEMAS ESPACIALES DE REFERENCIA
Latitud y longitud
Para ubicarnos en el espacio es preciso usar algun tipo de referencia. Y si queremos
compartir con otras personas esta ubicación es necesario además que estas referencias sean
de uso común.
El sistema de referencia más elemental a nivel global (mundial) es el sistema de latitud y
longitud también llamado phi (φ) lambda (λ) o coordenadas globales (Figura 1). Este
sistema mundial usa como referencias a los meridianos y los paralelos que son líneas
imaginarias que rodean al globo terráqueo.
Figura 1: Coordenadas en la esfera. Latitud (phi (φ)). Longitud (lambda (λ)). Distancia al
centro de la esfera p
Los paralelos son círculos imaginarios todos paralelos entre sí. El mayor es el que divide a
la tierra por el ecuador y se lo llama ecuador o paralelo cero. Los otros paralelos son de
perímetro menor y se los identifica por el ángulo que se forma entre el plano del ecuador y
el círculo paralelo al ecuador que pasa por un punto en cuestión. Este ángulo se mide con
signo positivo hacia el norte y negativo hacia el sur. Por ejemplo el campus de la
Universidad está en el paralelo 33º 07’ Sur. (o -33º 07’). Si una persona se desplazara por la
superficie terrestre a lo largo de un paralelo estaría moviéndose sólo hacia el este o hacia el
oeste.
Los meridianos son círculos imaginarios que contienen al eje de rotación terrestre y también
contienen a ambos polos. El meridiano cero (o meridiano origen) es el meridiano de
Greenwich (lugar del observartorio del mismo nombre ubicado en Inglaterra). Hacia el este
del meridiano cero, los meridianos se miden con valor positivo y hacia el oeste con valor
Apuntes del curso 2007 – Página 1 de 6
UNRC – AFIP – CURSO DE MANEJO MANEJO DE GEOPOSICIONADOR SATELITAL DE TIPO NAVEGADOR
negativo. Lo que se mide en ambos casos es el ángulo formado entre el plano determinado
por el meridiano origen y el plano formado por el meridiano que que contiene el punto en
cuestión. A este ángulo se lo denomina “longitud” del meridiano. Por ejemplo, el campus
universitario tiene una longitud de 64º 17’ Oeste (también se expresa como -64º 17’). Esto
significa que, desde el plano formado por el meridiano cero hasta el plano formado por el
meridiano del campus hay 64º 17’ hacia el oeste. Si una persona se desplazara a lo largo de
un meridiano sólo se movería hacia el norte o hacia el sur.
La distancia al centro de gravedad terrestre es el tercer elemento que se debe anotar para
ubicar precisamente un punto en la superficie. Sin embargo esta distancia no es utilizada por
ser poco práctico su uso. En su lugar se usa la distancia a un elipsoide o al geoide (altura
con respecto al nivel del mar).
Como el lector podrá ver, este sistema de notación es el sistema de notación polar aprendido
hace ya mucho tiempo en el secundario. El alternativo de este sistema polar es el sistema de
coordenadas cartesianas ortogonales (Figura 2).
Para el sistema de latitud longitud (polar) hay dos direcciones de referencia ¿Cuáles son?
¿Qué representa la magnitud del vector D en relevamientos geográficos?.
Problema para pensar (tiene solución lógica): Un hombre sale de la puerta de su casa, hace
exactamente 10 Km al sur, exactamente 10 Km hacia el oeste, exactamente 10 Km hacia el
norte. Está de nuevo en la puerta de su casa. Se encuentra con un oso ¿de que color es el
oso?
Figura 2: Sistemas de notación de la posición de un punto. Esta figura es esquemática y se
refiere a sólo dos dimensiones, en tanto que en los sistemas de posicionamiento
geográfico se requieren tres dimensiones.
Sistemas de Proyección
El sistema de latitud y longitud para ubicar un punto está muy bien, es conocido
mundialmente y cualquier persona del planeta entendida en el tema de cartografía va a
entender y poder ubicar un par de coordenadas expresada en este sistema. Pero se trata de un
sistema no proyectada, es decir que la superficie curva casi esférica del planeta no es
“forzada” a un sistema plano. ¿Qué ventajas tiene un sistema plano? Que en este sistema es
fácil medir distancias entre puntos, medir superficies, calcular volúmenes materiales, entre
otros además de la casi imperceptible ventaja de tener planos y mapas en formato de hoja
desplegable y no de un globo terráqueo.
El problema es que para llevar algo que es curvo a un superficie plana algo se tiene que
romper (si no prueben de pelar uina naranja sin romper la cáscara y “aplastar” la cáscara
contra la mesa. Así se han desarrollado muchos métodos para proyectar la superficie curva
(3D) del planeta a superficie planas (2D).
Apuntes del curso 2007 – Página 2 de 6
UNRC – AFIP – CURSO DE MANEJO MANEJO DE GEOPOSICIONADOR SATELITAL DE TIPO NAVEGADOR
En este apunte me voy a explayar sólo en los dos que más nos interesan a nuestros fines. El
sistema UTM (Universal Transverso de Mercator) y el TM (Transverso de Mercator) Gauss
Krüger que es el que se usa en la Argentina.
Veamos lo que es común a ambos sistemas. Son proyecciones cilíndricas transversas
(Figura 3).
Figura 3: Sistema de proyección cilíndrica.
Esto quiere decir que el plano de proyección es un cilindro imaginario que envuelve a la
tierra. Transverso significa que el eje del cilindro IMAGINARIO se dispone en forma
perpendicular (transversal) al eje de rotación terrestre.
Pero aquí se acaban la similitudes. En el sistema UTM el cilindro de proyección se dispone
secante al plano de la superficie terrestre, en tanto que en el sistema usado en la Argentina
se dispone en forma tangencial. Figura 4.
Figura 4: Disposición secante o tangente del cilindro de proyección respecto a la superficie
terrestre.
Una consecuencia lógica de estos dos sistemas es que a medida que aumenta la distancia
entre el o los meridianos donde el cilindro de proyección es secante o tangente a la
superficie terrestre mayor es la distorsión entre lo que existe en la superficie terrestre y su
representación en el plano de proyección. La forma en que esto es resuelto es crear “fajas” o
zonas de un ancho tal que las distorsiones sean aceptables. Por ejemplo, para el sistema
UTM, la primera posición del cilindro de proyección es en la zona 1 y utiliza una zona de 6º
de “ancho” (de extensión en sentido este – oeste). Luego se “reposisiona” el cilindro
girándolo 6º hacia el este de manera de generar la faja 2 y así sucesivamente. A su vez el
sistema UTM también está “fraccionado en sentido norte sur, formándose “celdas” de 6º de
extensión oeste – este y de 8º de extensión Norte – Sur. Más al sur de los 80º de latitud sur y
más al norte de los 80º de latitud norte, el sistema UTM es poco útil por la distorsión.
(Figura 5). Ejercicio para afianzar conocimientos. Diga en que zona UTM y en que letra se
ubica Río Cuarto.
Apuntes del curso 2007 – Página 3 de 6
UNRC – AFIP – CURSO DE MANEJO MANEJO DE GEOPOSICIONADOR SATELITAL DE TIPO NAVEGADOR
Figura 5: Sistema de proyección UTM.
Para el sistema TM Gauss – Krüger usado en la Argentina, el cilindro de proyección es
tangente a la superficie terrestre y no secante. La primera consecuencia de esto es que el
ancho de cada faja (o zona para UTM) no es de 6º sino de 3º (Figura 6).
Figura 6: Sistema de proyección
Gauss
–
Krüger.
Disposición de las fajas
en
la
república
Argentina. Como se
puede ver el número de
la faja crece hacia el este
y las longitudes crecen
hacia el oeste. Se ha
sombreado
el
área
cubierta por la Faja 3,
cuyo meridiano central es
el -63º o 63º Oeste. Los
meridianos
centrales
están marcados en azul y
los meridianos frontera
están marcados en azul.
Nótese que, debido a la
curvatura terrestre, el
ancho en metros de cada
faja va disminuyendo
hacia el sur.
Apuntes del curso 2007 – Página 4 de 6
UNRC – AFIP – CURSO DE MANEJO MANEJO DE GEOPOSICIONADOR SATELITAL DE TIPO NAVEGADOR
Como el lector podrá ver el sistema es absolutamente arbitrario pero con una lógica bastante
elegante. Y aquí se pone más arbitrario: Las coordenadas planas que se usan en el sistema
Gauss Krüger son un poquito complicadas. La variable espacial que marca las distancias
norte sur (de ahora en más, norteña o, como dice en los GPS, northing) se llama variable X
y tiene su valor cero metros en la latidud -90º o sea en el polo sur y aumenta hacia el norte.
Una consecuencia lógica de esto es que para todas las fajas del país la latidud de origen es el
polo sur y su falso origen es 0 metros. La que es un poquito más complicada es la variable
que mide las distancias oeste – este. Tiene su falso origen en cada uno de los meridianos
centrales de cada faja, se llama variable Y y aquí le vamos a llamar esteña o easting.
Aumenta hacia el este. La longitud de origen es el meridiano central de cada faja y el
llamado falso easting es un número compuesto por la n unidades de millón donde n es el
número de faja más 500.000 metros. Ejemplo. En el meridiano central de la faja 4 (-63º) la
coordenada easting es 4.500.000 metros. Cuatro millones por que es la faja 4 y medio
millón de metros para indicar que estoy en el meridiano central. ¿¿PORQUÉ?? Preguntará
el lector. Hay varias razones, bastante elegantes y lógicas. Al no haber un “cero” u origen
para todos, puede haber tantos orígenes como sea necesario (recuerde, está representando en
un plano algo que es esferoide). Por eso, cada faja tiene un origen diferente. La unidad de
millón de metros en cada faja es para identificar la faja en la que se observó el punto, y el
500.000 adicional es para que los puntos al oeste del meridiano central sigan teniendo la
unidad de millón de la faja a la cual pertenecen. Por ejemplo, en las cercanías del
Departamento de Geología, las coordenadas en Gauss Krüger son 4.378.800, 6.338.500.
Esto quiere decir que este punto está 121.200 metros al oeste del meridiano central de la faja
y a 6.338.500 metros al norte del polo sur.
¿Cotas o Alturas o Elevación?
Hasta ahora se ha visto como expresar la posición horizontal, es decir las coordenadas
esteña y la coordenada norteña. Pero falta la coordenada que exprese a que altura está un
punto. Hay básicamente dos sistemas de referencia. En la Figura 7 se ven el elipsoide de
referencia y el geoide. El elipsoide (Figura 8) se define como un cuerpo de revolución
(alrededor del eje Z) que puede ser expresado matemáticamente. Los GPS usualmente dan
la altura respecto a un elipsoide.
Figura 7: Relación entre el Geoide y el Figura 8: Elipsoide geodésico de referencia
elipsoide
El geoide se puede definir como la proyección sobre el continente de la altura media del
nivel del mar. Esta “proyección” se obtiene por nivelación diferencial (Figura 9. La altura
sobre el geoide es la más frecuentemente usada y también es llamada altura sobre el nivel
del mar (msnm). El problema es que el geoide no es una superficie matemáticamente
expresable.
Apuntes del curso 2007 – Página 5 de 6
UNRC – AFIP – CURSO DE MANEJO MANEJO DE GEOPOSICIONADOR SATELITAL DE TIPO NAVEGADOR
Figura 9: Nivelación diferencial
Figura 11: Relación entre altura ortométrica
y altura geodésica.
Apuntes del curso 2007 – Página 6 de 6
Figura 10: Altura ortométrica de un punto P
sobre el terreno.