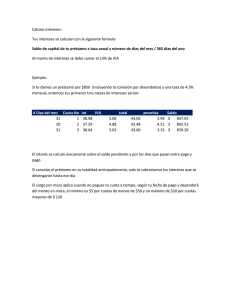
Matemáticas financieras apoyadas con Microsoft Excel

MATEMÁTICAS FINANCERAS
-Apoyadas con Microsoft Excel(Versión preliminar)
Julio A. Sarmiento Sabogal
Edgardo Cayón Fallon
Bogotá D.C., Junio de 2005
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Pontificia Universidad Javeriana
Facultad de Ciencias Económicas y Administrativas
Departamento de Administración
Reservados todos los derechos
© Julio Sarmiento Sabogal
© Edgardo Cayón Fallón
Edición:
Por definir
Diseño de portada: Andrés H. Mejía V.
Primera Edición: 2003
ISBN: XXXX
No. de ejemplares: XXX
Fotomecánica e Impresión: XXX
2
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Tabla de contenido
1.
El concepto de inversión .................................................................................5
1.1.
La tasa de descuento o tasa de retorno mínima aceptable.....................9
1.2.
Componentes de la tasa de interés. ......................................................14
Componente inflacionario..............................................................................14
Componente de riesgo ..................................................................................16
1.3.
La tasa de interés cuando existe mas de un período: El interés simple y
el interés compuesto. ........................................................................................17
2.
Factores de conversión .................................................................................22
2.1.
Valor Futuro (VF)....................................................................................23
Cálculo de VF a partir de una suma presente...............................................24
Cálculo de VF a partir de una suma presente con tasa no constante. .........27
Cálculo de VF a partir de una serie de cuotas uniformes. ............................30
Cálculo de VF a partir de una serie de cuotas no uniformes. .......................34
2.2.
Valor Presente (VP) ...............................................................................37
Cálculo de VP a partir de una suma futura ...................................................38
Cálculo de VP a partir de una suma futura con tasa no constante...............39
Cálculo de VP a partir de una serie de cuotas uniformes.............................42
Cálculo de VP a partir de una serie de cuotas no uniformes........................44
Cálculo de VP a partir de una serie de cuotas no uniformes y tasa no
constante .......................................................................................................47
2.3.
3.
Ejercicios ................................................................................................50
Tasas Equivalentes .......................................................................................52
3.1.
Intereses anticipados y vencidos ...........................................................52
3.2.
Tasas nominales y efectivas ..................................................................55
Tasa de interés efectiva ................................................................................59
Tasa de interés nominal ................................................................................60
Tasa de interés Periódica..............................................................................61
3
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Relación entre las tasas efectivas, nominales y periódicas..........................63
La funcionalidad de las tasas efectivas.........................................................65
Ejercicios .......................................................................................................66
4.
Tablas de amortización .................................................................................70
4.1.
Componentes de una tabla de amortización. ........................................70
4.2.
Tipos de tablas de amortización ............................................................71
4.3.
Tablas de amortización cuando se define la cuota................................71
Tablas de amortización con cuota fija ...........................................................72
Tablas de amortización de cuota fija cuando se tienen tasas variables.......78
Tablas de amortización de cuota ascendente o descendente......................81
4.4.
Tablas de amortización con abono a capital uniforme ..........................85
Tablas de amortización con abono a capital uniforme..................................86
5.
Ejercicios Integradores ..................................................................................89
6.
Glosario .........................................................................................................92
7.
Resumen de fórmulas ...................................................................................96
4
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
1. El concepto de inversión
El diccionario define inversión como "Un sacrificio de recursos hoy, con la
esperanza de recibir un beneficio en el futuro".
Al examinar detenidamente este concepto se puede encontrar que una inversión
es un "sacrificio" porque que la mayoría de los seres humanos prefirieren
consumir en el presente a hacerlo en el futuro, cuando una persona invierte, deja
de consumir para entregar su dinero a otro, esperando que se le recompense
por su sacrificio. Para ilustrar este concepto recurriremos a un ejercicio que
solemos usar en nuestras clases:
Ejemplo 1.1
Imagine que Usted no tiene vehículo, pero que hoy dispone de suficiente dinero
para comprar de contado un vehículo Sprint último modelo (2005), y alguien le
propone que le preste ese dinero y que a cambio le entregará en el año
siguiente (2006), el mismo Sprint modelo 2006. ¿Aceptaría usted ese negocio?.
Su respuesta seguramente será un rotundo NO, Usted no esta dispuesto a
postergar la compra de su automóvil por un año a cambio de recibir el mismo
carro. Pero si la persona que le propuso el negocio, le ofrece un Corsa,
seguramente Usted pensaría en que se puede sacrificar un año, a cambio de
recibir un carro de una gama superior, pero para aquellos que siguen pensando
que el negocio no les es favorable, ¿qué opinarían si a cambio les ofrecen un
Epica?. Seguramente habrá personas que acepten la opción del Corsa, porque
creen que es un buen “retorno” de su sacrificio y otras que no quieran aceptar la
opción del Epica1.
1
Para quienes no estén familiarizados con el tema, el Sprint es la gama más baja de la marca
Chevrolet, el Corsa es un vehículo de gama media y el Epica es el vehículo de gama alta de la
marca en Colombia.
5
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Del ejercicio anterior se pueden extraer varias conclusiones:
•
Las personas no invierten para recibir a cambio lo mismo que hubiesen
podido consumir sin invertir, es decir, si se quiere que alguien invierta, se
le debe recompensar.
•
Cada persona tiene un nivel requiere de una recompensa o retorno
diferente, pues su decisión depende factores subjetivos absolutamente
respetables como por ejemplo qué tanto necesita su carro en el momento,
cuanto tiempo lleva esperando para tenerlo etc. Por ejemplo, dos
personas a las que se les ofrece el mismo trato de cambiar el Sprint hoy,
por un Corsa dentro de un año, tienen respuestas diferentes. El primero
es un estudiante que vive a unos pocos metros de su universidad, él
podrá aceptar con mucha mayor facilidad que un padre de familia que
vive en una gran ciudad y que todos los días debe llevar a sus dos hijos,
de uno y tres años al jardín, que queda a varios kilómetros de distancia de
su casa y después debe ir a su trabajo y en tarde debe repetir el recorrido
en sentido inverso.
Una inversión además es un sacrificio de "Recursos", observe que las
inversiones no solamente se hacen en dinero, sino en general, puede invertirse
cualquier bien o servicio deseable y escaso. Por ejemplo, los activos fijos
(computadores, construcciones, maquinaria etc.), el conocimiento o el tiempo, en
general todo lo que el inversionista entrega debe ser considerado y cuantificado.
Esto implica un problema asociado a la valoración de los activos, por ejemplo
imagine que usted va ha invertir en su nuevo negocio un computador que
compró hace 6 meses y costó $1.000.000 (valor de compra), adicionalmente
usted lleva su contabilidad personal, en la cual el computador aparece con un
valor de $833.333 (valor en libros). Un computador usado con características
similares al suyo se negocia por $500.000 (valor de mercado), pero si Usted no
6
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
entrega el suyo necesitaría comprar uno nuevo que cuesta aproximadamente
$1.100.000 (valor de reposición), ¿Cuál de estos valores se tomará como el
monto de la inversión que Usted hizo al ceder el computador al nuevo proyecto?,
Normalmente se usa el valor de mercadi para determinar el valor de los activos,
sin embargo embargo se puede encontrar abundante literatura sobre el tema de
valoración de activos.
Ahora analicemos la palabra "Hoy", el tiempo es el concepto más importante
dentro de las matemáticas financieras debido a que el dinero tiene sentido como
recurso únicamente cuando se retiene por un tiempo determinado. Para aclarar
esta idea, suponga que Usted le entrega a alguien $1.000.000 y esta persona le
entrega inmediatamente otros billetes de la misma moneda por el mismo valor.
¿Considera Usted que ha realizado algún negocio? ¿ganó o perdió algo por esa
transacción?, seguramente su respuesta será NO (aquí no se están teniendo en
cuenta los costos de transacción), pero si en el mismo caso, la persona le
devuelve el mismo millón de pesos pero un año más tarde ¿Usted lo recibiría sin
ninguna objeción?, lo más probable es que no, ha pasado un tiempo y Usted
esperaría recibir más de lo que le entregó a esta persona. Observe que Usted no
encuentra sensato pensar que un millón de pesos de hoy es el mismo millón
dentro de un año; el significado de estos valores es diferente y por lo tanto no
son comparables2.
Por otra parte la "Esperanza" nos recuerda que siempre que se invierte se está
corriendo el riesgo de perder una parte o toda la inversión, no hay realmente en
el mundo ninguna inversión absolutamente libre de riesgo, aunque para efectos
prácticos en el mercado financiero internacional se considera que los bonos del
tesoro de los Estados Unidos son libres de riesgo y en el mercado colombiano
2
¡¡¡A menudo decimos en nuestras clases que sumar dos millones de hoy con tres millones
entregados en un año, sería semejante a sumar 2 peras con 3 gatos…!!!
7
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
los TES (Títulos de Emisión Soberana emitidos por el Ministerio de Hacienda y
Crédito Público) son considerados cero riesgo.
Por último nos encontramos con los "Beneficios", estos son la razón por la cual
se invierte y para que estos existan se debe recuperar lo invertido y generar
excedentes, a estos excedentes comúnmente los llamamos intereses.
En finanzas se acostumbra dar algunos nombres diferentes a las cifras que
manejamos cotidianamente. A las inversiones se les llama VALOR ACTUAL, o
VALOR PRESENTE, porque la definición de inversión dice que esta es un
sacrificio de recursos hoy. A los beneficios, que están situados “en el futuro”, se
les llama VALOR FUTURO. La rentabilidad, que es la medida en términos
porcentuales del rendimiento de un capital determinado, se le llama TASA DE
INTERES y a la Utilidad producida por la inversión se le llaman INTERESES.
Tabla 1.
Términos usados en la matemática
financiera
Nombre Común
Inversión
Ingresos / Beneficio
Rentabilidad
Utilidad
Matemática financiera
Valor Actual (VA)
Valor Presente (VP)
Valor Futuro (VF)
Tasa de interés (i)
Intereses (I)
Ahora debemos encontrar un valor de intereses que haga que la persona decida
sacrificarse e invierta en lugar de consumir. En general, más que un valor
absoluto del monto de los intereses, buscamos una tasa de rentabilidad a la cual
el inversionista decida invertir. A esta tasa se le llama Tasa de Descuento, Tasa
de Oportunidad o Tasa de Retorno Mínima Aceptable. Observe que esta tasa es
de absoluta importancia, pues es una tasa de inflexión de la decisión: por debajo
de esta preferirá consumir antes que ahorrar, y por encima decidirá invertir.
8
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
1.1. La tasa de descuento o tasa de retorno mínima aceptable.
Ejemplo 1.2
Suponga que Ud. ha venido guardando dinero debajo de su colchón, para
comprar una agenda electrónica, que, aunque no es indispensable, le gustaría
tener. Ya tiene un millón de pesos ahorrados. Yo le he pedido prestado ese
dinero por un año y Ud. ha pensado que no sería una mala idea, pues le he
ofrecido un respaldo que hace virtualmente imposible que se pierda el dinero o
se demore siquiera un día mas del plazo fijado.
Ahora estamos negociando el valor que yo le debo entregar el próximo año.
Observe que Usted tiene dos opciones, compra su agenda electrónica o me
presta el dinero a mi. ¿Cuánto sería lo mínimo que me cobraría dentro de un
año?. Piense en un valor que haga que Ud. se “sacrifique” por un año al no
comprar el aparato. ¿cuánto sería?
$_____________. ¡¡¡Realmente me parece que la suma que Ud. acaba de
poner es demasiado alta!!!, por favor, piense en la mínima suma que Usted me
cobraría por ese préstamo $_____________. Bueno, le ofrezco un peso menos
de lo que Usted acaba de escribir. ¿Acepta este negocio? Si Ψ, No Ψ.
Si la respuesta fue si, por favor piense por última vez cuál sería la mínima cifra
que estaría dispuesto a recibir $_____________.
ACABA USTED DE HALLAR SU TASA DE DESCUENTO. Por favor permítanos
explicarle
Observe que trabajar con valores es engorroso, si nosotros cambiáramos la cifra
de un millón, por cincuenta millones, Usted debería cambiar ese valor y volver a
realizar el ejercicio por eso, siempre se trabaja con tasas de interés.
9
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Calculemos entonces la tasa de interés que Usted decidió que era su tasa de
descuento:
VF
−1
VA
(1)
I = VF-VA
(3)
i =
i=
ó
I
VA
(2)
Suponiendo que Ud. dijo que lo mínimo que esperaba en un año era $1.150.000,
tendríamos:
i =
1.150.000
− 1 = 0,15
1.000.000
ó
15%
Usando las ecuaciones (2) y (3)
I = 1.150.000 − 1.000.000 = 150.000
i =
150.000
= 0,15
1.000.000
ó
15%
Ahora por favor Ud. haga lo propio con los valores que eligió:
i =
1.000.000
− 1 = ______
ó
______%
Usando las ecuaciones (2) y (3)
I = _________ − 1.000.000 = _________
i =
1.000.000
= ______
ó
________%
La tasa de descuento es aquella a la cual un inversionista, que tiene una sola
oportunidad de inversión decide invertir. Esto supone que ha decidido sacrificar
su consumo inmediato para recibir en cambio una suma mayor en el futuro.
Observe que esta tasa es la que hace equivalente el consumo de hoy a un
consumo superior dentro de un periodo de tiempo. Si se le ofrece a este
inversionista una tasa menor, decidirá consumir ahora, si por el contrario, la tasa
es mayor, la persona optará por invertir.
10
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
NO
INVIERTE
sió
er
v
n
i
n
la
de
d
a
ilid
tab
n
Re
SI INVIERTE
Tasa de
descuento
Piense un momento detenidamente por favor el significado de la frase:
“Observe que esta tasa es la que hace equivalente el consumo de
hoy a un consumo superior dentro de un periodo de tiempo. Si se le
ofrece a este inversionista una tasa menor, decidirá consumir ahora,
si por el contrario, la tasa es mayor, la persona optará por invertir” .
En realidad, la tasa de descuento materializa el concepto de equivalencia, que
muestra que existe un nivel de rentabilidad a la cual el inversionista será
indiferente consumir ahora o invertir. Usando la ecuación (1) podríamos decir
que:
VF = VA * (1 + i)
(4)
Y siguiendo con nuestro supuesto encontraríamos que:
VF = 1.000.000 * (1 + 0,15) = 1.150.000
Ahora hagámoslo con su tasas de descuento :
VF = 1.000.000 * (1 + ______) = ______________
Podemos concluir entonces que para Usted es lo mismo consumir $1.000.000
hoy o consumir $____________ dentro de un año. Si yo le ofreciera menos de
11
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
este valor Usted preferiría comprar su agenda digital y si yo le ofreciera un valor
superior a esta suma Usted preferiría invertir.
Ahora por favor consiga cinco valores futuros que otras personas hayan anotado
en este mismo ejercicio. 1)_____________, 2)_____________,
3)_____________, 4)_____________, 5)_____________ .
¿Son iguales estos valores? ¿coincide alguno de estos con el suyo?, muy
seguramente la respuesta será NO, entonces ¿Alguno de estos valores es más
acertado que los demás?, ¿será que alguna de las personas que le dio un valor
tiene la razón sobre cuál es el valor adecuado y Usted no? ¿será lo contrario?.
La respuesta a estas preguntas es NO. Todos los valores son igualmente
válidos, esto, porque el millón de pesos es su dinero y solo Usted puede decidir
que hacer con él. Adicionalmente la tasa de descuento es subjetiva, cada
inversionista tiene su propia tasa de descuento, y sea esta alta, media o baja
(comparada con las de las otras personas) es igualmente correcta y respetable.
En la economía se empieza a encontrar que las tasas de interés están casi
todas dentro de un mismo rango, si el inversionista pone un valor por encima de
este rango, nadie estará dispuesto a pagar un costo tan alto por su dinero, si por
el contrario cobrase demasiado poco, estaría perdiendo dinero si se compara
con lo que estarían dispuestos a pagar quien lo requieren.
Por eso estudiaremos
como explica la economía, desde un punto de vista
formal, cómo se forman las tasas de interés: Según Fisher (1930), la tasa de
interés es el resultado de la unión de varios componentes, en principio, Fisher
propuso que estos componentes eran la inflación y el interés real. Mas tarde se
incluyó el riesgo como un tercer componente adicional. Es decir:
Ic = (1+if) x (1+ir) x (1+iθ) – 1
(5)
12
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Donde Ic es la tasa de interés, if es el componente de inflación, ir representa el
componente real e iθ es el componente de riesgo.
13
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
1.2. Componentes de la tasa de interés.
Componente inflacionario
La inflación es la Medición del crecimiento del nivel general de precios de la
economía. La inflación es calculada mensualmente por el DANE sobre los
precios de una canasta básica de bienes y servicios de consumo para familias
de ingresos medios y bajos (Canasta Familiar). En Colombia se utiliza el IPC
(Indice de Precios al Consumidor) para su cálculo. Esta medida se basa en la
medición de la canasta familiar en diferentes ciudades. Esta canasta familiar
esta compuesta por diferentes grupos de gasto como alimentación, vestuario,
e.t.c. y para cada uno de los estratos socio-económicos.
El sistema financiero colombiano vivió una de las más agudas crisis de su
historia a causa del UPAC, un sistema creado en 1972 para incentivar la oferta
de créditos de vivienda de largo plazo, que en últimas lo que buscaba era blindar
las inversiones contra las variaciones de la inflación, que en Colombia
históricamente ha sido siempre bastante volátil.
14
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Variación IPC en Colombia 1955 - 2003
40
variacion porcentual
35
30
25
20
15
10
Variación IPC
5
0
1955
1965
1975
Promedio
1985
1995
Sin embargo a partir de marzo de 19933 se eliminó totalmente la inflación de la
base del cálculo del UPAC, por lo cual, un sistema que había sido creado en sus
orígenes para remunerar el componente inflacionario de la tasa de interés, se
desfiguró, haciendo que el UPAC aumentara un 28.38% más que IPC en el
período 1997-1999.
AÑO
1993
1994
1995
1996
1997
1998
1999
Variación del
Variación del
UPAC*
IPC**
23,3%
22,60%
24,3%
22,59%
20,1%
19,46%
18,8%
21,63%
20,2%
17,68%
27,1%
16,70%
24,7%
9,23%
Diferencia
0,74%
1,66%
0,68%
-2,79%
2,52%
10,39%
15,47%
* Fuente: Banco de la República
** Fuente DANE
Este es un panorama bastante complejo si se recuerda que en estos créditos, la
tasa de interés se divide dos partes: por un lado el UPAC que reconoce,
3
Instituto Colombiano de Ahorro y Vivienda (ICAV). “EL UPAC, ANTECEDENTES DEL ACTUAL
SISTEMA DE FINANCIACIÓN DE VIVIENDA.”.
http://www.icav.com/secciones/uvr/upac.htm?ICAV=f1bace5c62a5c115d12267fa51748d60
15
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
supuestamente la inflación, y unos puntos adicionales que reconocen los otros
dos componentes de la tasa de interés.
Diferencia entre la variación del UPAC y el IPC
20,00%
15,00%
10,00%
5,00%
0,00%
1993
-5,00%
1994
1995
1996
1997
1998
1999
Fuente: Elaboración propia con base en Banco de la República y DANE
Componente de riesgo
Existen diferentes metodologías para la medición del riesgo de una inversión,
una de ellas consiste en medir los diferentes niveles de riesgo y combinarlos
aplicables a una inversión, estos diferentes son:
a) riesgo país: que mide los riesgos de una economía para los inversionistas
extranjeros el cual puede ser obtenido por medio de los Spreads o metodologías
como la ICRG (International Country Risk Guide), b) riesgo sector: que mide el
riesgo asociado propio de la actividad económica desarrolla y c) . Este puede ser
obtenido por varias vías: Usando los Spreads o Cálculos usados por compañías
calificadoras de riesgo como Standard and Poors, Moody’s o Fitch Ratings.
16
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
1.3. La tasa de interés cuando existe mas de un período: El interés
simple y el interés compuesto.
Hasta ahora hemos tomado ejemplos en donde solamente existe un período de
inversión, esto, porque cuando se trabaja con más de un período existen dos
formas de cálculo de los intereses. Para explicar esta situación recurriremos a
una anécdota personal.
Ejemplo 1.3
Cuando estaba en el colegio, tenía un amigo al que su Papá le daba un dinero
para que comiese algo. Resulta que por lo general le sobraba alguna pequeña
cantidad, y nosotros sus compañeros, que sabíamos de esta situación, le
pedíamos siempre que les prestara pero nunca me pagaban. Aburrido, mi
amigo decidió que en lugar de perder el dinero, iba a hacer un negocio con éste.
Entonces, un día, cuando alguien le pidió prestado $100 le dijo que sí, pero que
al día siguiente le debería pagar $110. ¡¡¡el 10% diario!!! era lo que cobraba mi
amigo. Estará Usted escandalizado por esta tasa tan alta. Pero en honor a la
verdad, mi amigo debía cobrar esa tasa tan alta, porque la moneda de más
pequeña denominación en ese entonces era de $10. ¡¡¡Si nos hubiese cobrado
menos, no hubiésemos podido pagarle!!!.
Un día, yo necesitaba un dinero
urgente para comprar los materiales de un trabajo y le pedí prestados $1.000. Al
día siguiente olvidé pedir el dinero para pagar, por lo que solo pude hacerlo al
segundo día. Cuando llegué a pagarle, le entregué $1.200, pero el me dijo que
en realidad le tenía que pagar $1.210.
¿Por qué me estaba cobrando mi amigo $1.210?
17
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Para empezar, podemos ilustrar el ejemplo con un Diagrama de Flujo de Caja, el
cual muestra esquemáticamente los problemas financieros, este diagrama se
compone de una línea horizontal que representa el tiempo. En el extremo
izquierdo una división que representa el período 0 o momento 0, que es el
momento en el que se realiza la inversión. El extremo derecho representa el
último período de inversión y cortes intermedios que representan el final de cada
período. Flechas hacia abajo que representan inversiones y hacia arriba que
muestran los ingresos.
Explicación del diagrama de flujo de caja
1.000.000
Fin del periodo
0
1
Ingresos
2
n
Tiempo
(1.000.000)
Egresos
El diagrama del problema desde mi punto de vista sería entonces:
1.210
i%=10% Diario
0
2
1
1.000
18
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Observe que los mil pesos fueron una entrada para mí, por eso aparece
representado por una flecha hacia arriba en el periodo cero, y los mil doscientos
son un egreso en el segundo periodo.
La representación del problema para mi compañero sería:
1.210
i%=10% Diario
0
2
1
1.000
Bueno, pero regresemos al problema: Yo pensaba que debía pagar $1.200,
pues pensaba que debería devolver los $1.000 que me había prestado y $200
de dos días de intereses de intereses de dos días. Pero mi compañero me
explicó que a mi cuenta había que adicionarle $10 de intereses de los cien que
no había cancelado de intereses el primer día.
Años después, ya en la Universidad entendí que el cálculo que yo había
realizado, se conocía como “Interés simple” en este, se cobran intereses
únicamente sobre la suma inicial de la inversión. Y lo que mi amigo había hecho
se conocía como “Interés Compuesto”, que supone que los intereses se cobran
sobre la suma inicial y sobre los intereses causados y no pagados.
Este último sistema, se ha tendido a satanizar en Colombia y los abogados le
han llamado Anatosismo, de hecho la Corte Constitucional lo declaró
inconstitucional y por lo tanto inaplicable en el país. Sin embargo este se usa en
todo el sistema financiero internacional, y la razón conceptual para esto se
puede explicar muy fácilmente con el ejemplo anterior por medio de la siguiente
reflexión: Mi amigo me cobraba intereses diarios de $100, al no pagar los
19
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
intereses del primer día, yo ocasioné que él no pudiera prestar ese dinero a otra
persona y por lo tanto había perdido el valor de los intereses que le hubiesen
generado los cien pesos, es decir había perdido diez pesos ($100*10%) .
Entonces ¿quién debía asumir esta pérdida?. Seguramente los 10 pesos debían
ser asumidos por mí, que era quien tenía y estaba usando el dinero durante ese
período de tiempo. Observe que quien tiene el dinero es quien debe pagar por
este, y por lo tanto, el sistema conceptualmente correcto desde el punto de vista
financiero es el Interés Compuesto.
Matemáticamente el interés compuesto completa nuestra fórmula (4) al elevar la
fracción (1 + i) al número de períodos de la inversión.
VF = VA * (1 + i)n
(6)
La fórmula (6) es una de las bases más importantes en finanzas, esta se usa o
de ella se extraen modelos tan simples como saber cuánto será lo que se reciba
por una inversión, hasta temas avanzados como cálculo de precio de
instrumentos derivados.
Cuando se tiene mas de un período, se deben agregar dos términos a nuestra
tabla:
Tabla 2.
Términos usados en la matemática
financiera - Completa
Nombre Común
Matemática financiera
Valor Actual (VA)
Inversión
Valor Presente (VP)
Ingresos / Beneficio Valor Futuro (VF)
Rentabilidad
Tasa de interés (i)
Utilidad
Intereses (I)
Número de períodos (n) o (Nper)
Cuotas o pagos
Cuotas o pagos
20
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Aquí aparece un nuevo término llamado cuota o pago. Que aparece cuando en
lugar de recibir una sola suma al final de la inversión (VF), se le entregan una
serie de pagos en los periodos intermedios. Estas cuotas pueden ser cuotas
uniformes en donde se le entrega exactamente en mismo monto durante todos
y cada uno de los periodos, o cuotas no uniformes en el caso en el que los
montos entregados difieran en algún periodo. Adicionalmente vale la pena
mencionar que cuando existe más de un período las fórmulas (1) y (2) no se
pueden usar.
21
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
2. Factores de conversión
La fórmula (6) nos permite calcular cuanto va a recibir un inversionista en el
futuro, o en otras palabras calcular el “beneficio” del que hablamos en la
definición de Inversión. Observe que esta fórmula tiene 4 factores, Valor Actual,
Valor Futuro, tasa de interés y número de períodos. En este capítulo
observaremos cómo se pueden calcular cada uno de estos, siempre y cuando
tengamos la información de otros tres de ellos y que por lo menos uno de ellos
sea o la tasa de interés o el número de períodos.
Suma Futura: Se puede calcular a partir de una suma presente, a partir de una
serie de cuotas uniformes o a partir de una serie de cuotas no uniformes.
También se puede trabajar con tasas de interés iguales para todos los periodos
o con tasas de interés diferentes en cada uno de estos.
Suma presente: Se puede calcular a parir de una suma futura, una serie de
cuotas uniformes o a partir de una serie de cuotas no uniformes. También se
puede trabajar con tasas de interés iguales para todos los periodos o con tasas
de interés diferentes en cada uno de estos.
Serie de cuotas uniformes -> Suma presente
Suma presente -> Serie de cuotas uniformes
Suma Futura -> Serie de cuotas uniformes
Serie de cuotas uniforme -> Suma Futura
Cálculo de la tasa de interés
Cálculo del número de Períodos
El cálculo de estos factores se mostrará de dos maneras: En primera instancia
realizaremos el planteamiento matemático y en segundo lugar se resolverá el
ejercicio usando como Herramienta Microsoft Excel, que es una de las
22
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
herramientas más sencillas para eliminar los problemas de la formulación
matemática propia de este tema.
2.1. Valor Futuro (VF)
Representa un solo flujo de dinero que se entrega al final del último período de
inversión. Se puede calcular a partir de una suma presente, una serie de cuotas
uniformes o a partir de una serie de cuotas no uniformes. También se puede
trabajar con tasas de interés iguales para todos los periodos o con tasas de
interés diferentes en cada uno de estos. Es decir, antes de saber la fórmula
correcta para el cálculo se debe revisar si se cumplen o no los siguientes
supuestos:
Pagos
uniformes
Períodos
iguales
Tasa
constante
Tabla 3.
Opciones para el calculo del Valor Futuro
N.A.
SI
SI
VA * (1 + i ) n
N.A.
SI
NO
VA * [(1 + i1 ) * (1 + i2 ) * ..... * (1 + in )]
Una cuota
uniforme
SI
SI
SI
PAGO * ⎢
Una cuota
NO uniforme
NO
SI
SI
Cálculo de
VF a partir
de:
Una suma
presente
Una suma
presente
Una cuota
NO uniforme
NO
SI
NO
Fórmula
Función en
Excel
VF
⎡ (1 + i ) n − 1 ⎤
⎥
i
⎣
⎦
PAGO1 * (1 + i )n −1 + PAGOt * (1 + i )n −t + ...
PAGOn −1 * (1 + i )1 + PAGOn
PAGO1 * [(1 + i 1 ) * (1 + i 2 ) * ..... * (1 + i n )] + ...
PAGO 2 * [(1 + i 2 ) * ..... * (1 + i n )] + ...
PAGO n −1 * [(1 + i n )] + ...
PAGO n
23
VF.PLAN
VF
No existe
No existe
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Cálculo de VF a partir de una suma presente
Su fórmula matemática es:
VF = VA * (1 + i)n
(6)
Ejemplo 2.1
¿Cuánto recibirá Luisa Fernanda en 12 meses, si ha invertido $1.000.000 a una
tasa del 2% mensual?.
El diagrama de flujo de caja del problema es:
VF=?
i = 2%
0
12
$1.000.000
El planteamiento matemático del problema es:
VF = 1.000.000 * (1 + 2%)12 = $ 1.268.241,79
Tal como habíamos anunciado arriba, resolveremos ahora el problema usando
como herramienta Microsoft Excel. En primera medida debemos incluir en las
celdas de Excel los datos del problema:
Después debemos llamar al asistente de funciones del programa. Esto se puede
hacer buscando el botón en la barra estándar o en el menú “Insertar”, escoger la
opción “Función”:
24
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Dentro del menú de funciones, se escogen las funciones financieras y allí se
busca la función con el nombre del factor de conversión que se está buscando.
En este caso debemos buscar la Función VF:
25
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
En este momento aparecerá el cuadro de diálogo de la función:
Fórmula que se desea aplicar
Estos elemento se explicarán más adelante
(Por favor déjelos en blanco)
Area de explicación de la fórmula
Area de explicación de la variable en
uso
Resultado obtenido
En el extremo superior izquierdo aparece el nombre de la función que se va a
calcular, en este caso es VF. En los siguientes cuadros se preguntan todos los
posibles argumentos de la función, de los cuales llenaremos los que eran
pertinentes y los demás los dejaremos en blanco. En este caso tenemos Tasa,
Nper y VA. En la segunda parte del cuadro siempre aparecerá la información de
la Función que se ha llamado y la explicación del argumento sobre el cual esta
ubicado el cursor. Observe que en el cuadro anterior el cursor estaba en VA y
por lo tanto el segundo párrafo de explicación corresponde a la de VA. Por
último el cuadro muestra el resultado de la función, en caso de que no muestre
un número, significa que faltan argumentos o que alguno de ellos es incorrecto.
El resultado es el mismo que calculamos con la fórmula matemática:
Sintaxis de la fórmula
26
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
El resultado es negativo porque Excel supone que si al comienzo el flujo de caja
es positivo (como se muestra en el gráfico anterior), significa que se ha otorgado
un préstamo y por supuesto el VF será el pago del préstamo, si por el contrario,
al comienzo se hace una inversión, al final del flujo se dará el retorno positivo.
Cálculo de VF a partir de una suma presente con tasa no constante.
Este caso ocurre cuando la tasa proyectada para cada periodo es diferente. En
realidad esta en nuestra opinión es la mas común de las situaciones en la vida
práctica, pues los componentes de la tasa de interés la tasa de interés cambian
constantemente y por supuesto esta con ellos.
Su fórmula matemática es:
VF = VA * [(1 + i 1 ) * (1 + i 2 ) * ..... * (1 + i n )]
(7)
Ejemplo 2.2
Pedro Pablo es un inversionista que quiere colocar hoy una tasa de $1.000.000
a cinco años. Ha estado haciendo averiguaciones y ha concluido que la tasa de
interés que
para este año es del 10% anual, decrecerá un 1% cada año
durante su inversión. ¿ Cuánto recibirá en cinco años ?
27
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
El diagrama de flujo de caja del problema es:
VF=?
10%
9%
8%
7%
6%
1.000.000
El planteamiento matemático del problema es:
VF = 1.000.000 * [(1 + 0,1) * (1 + 0,09) * (1 + 0,08) * (1 + 0,07) * (1 + 0,06)]
VF = 1.468.698,26
Tal como se mostró en la Tabla 3, en Excel el ejercicio se debe resolver usando
la función VF.PLAN, sin embargo, algunas funciones (entre ellas VF.PLAN) que
por lo general no están cargadas en el programa. Para poder usarlas vaya al
menú “Herramientas”, y seleccione “Complementos”, busque y chulee
“Herramientas para análisis”
28
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Ahora podemos solucionar el problema usando VF.PLAN, esta función solo tiene
dos argumentos: “Capital” y “Serie de tasas”, en el primero incluiremos el monto
invertido y en el segundo seleccionaremos el rango de tasas futuras. Observe
que no es necesario incluir los periodos pues Excel lo calcula a partir del número
de tasas incluidas. Nótese además que esta función no cambia de signo como lo
hacía VA.
29
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Cálculo de VF a partir de una serie de cuotas uniformes.
Recordemos que las cuotas uniformes son una serie de flujos de caja
exactamente iguales durante todos y cada uno de los periodos de la inversión.
Su fórmula matemática es:
⎡ (1 + i ) n − 1⎤
⎥
i
⎣
⎦
VF = PAGO * ⎢
(8)
30
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Ejemplo 2.3
Carlos Humberto es un padre de familia quiere empezar a ahorrar a partir del
próximo mes y durante 6 meses $50.000 para las vacaciones de final de año,
en el fondo de ahorro de su compañía le han dicho que le pagarán un interés
del 2%.
¿ De cuánto dispondrá para sus vacaciones ?
El diagrama de flujo de caja del problema es:
VF=?
0
1
2
3
4
5
50.000
El planteamiento matemático del problema es:
⎡ (1 + 0,02) 6 − 1⎤
VF = 50.000 * ⎢
⎥
0,02
⎦
⎣
VF = 315.406,05
En Excel el problema se resuelve de nuevo con la función VF, pero ahora no
tendremos VA, sino que únicamente tendremos PAGOS.
31
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Observe que el flujo que diseñamos supone que se empieza a ahorrar no hoy,
sino dentro de un mes, adicionalmente la persona tendrá que pagar la última
cuota justo antes de que se empiece el viaje. ¿Qué pasaría si en lugar de
comenzar al final del primer mes, el señor pagase la primera cuota hoy mismo?.
La última cuota se pagaría un mes antes de viajar, de lo contrario terminaría
pagando 7 cuotas en lugar de 6. La entidad podría entregar el dinero entonces
en el periodo 5 como se muestra en el gráfico:
VF=?
0
1
2
3
4
5
50.000
Para la solución de este nuevo problema se puede usar el argumento “tipo”,
dándole valor 1, que significa anticipado.
32
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Otra opción del mismo problema 2.3, es que la persona ahorre durante los
periodos 0 al 5 (como en el caso anterior), pero que el fondo de ahorro solo
entregue el dinero en el periodo 6, como se observa en el diagrama:
VF=?
0
1
2
3
4
5
50.000
Este planteamiento no se puede solucionar usando una sola función o fórmula,
por lo que la solución se deberá dividir en dos pasos. En primer lugar
calcularemos el VF de una serie de pagos anticipados, tal como se hizo en el
caso anterior, esto nos dará el valor ahorrado en el período 5, el segundo paso
será pasar ese VF1 al periodo 6, como se muestra en el siguiente diagrama:
33
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
VF1
0
1
2
3
4
5
VF2=?
6
50.000
La solución de este ejercicio en Excel se dividirá también en dos pasos, primero
calcularemos el VF de una serie de pagos uniformes anticipados y después
calcularemos el VF a partir de un VA, como se muestra a continuación:
PASO 1
PASO 2
Cálculo de VF a partir de una serie de cuotas no uniformes.
Las cuotas no uniformes son una serie de pagos en los periodos intermedios, en
los que los montos difieren en alguno o todos los periodos. Su fórmula
matemática es:
34
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
VF = PAGO1 * (1 + i )n −1 + PAGOt * (1 + i )n −t + ... + PAGOn −1 * (1 + i )1 + PAGO n
Ejemplo 2.4
El 31 de diciembre del 2003 Javier Antonio decidió comenzar a ahorrar para su
pensión voluntaria, para lo cual entregó a WF Investments la suma de U$1.000.
Después de hacer cuentas, encontró que era prácticamente imposible
conservar su nivel debido a los mayores gastos en la educación de sus hijos,
así que encontró que su consignación de cada año disminuiría en U$100. Si la
compañía de inversión obtiene una rentabilidad del 10% anual, ¿Cuánto dinero
ahorrado tendrá después de hacer su consignación el 31 de diciembre de 2010?
El diagrama de Flujo de Caja del problema sería:
VF=?
0
1000
1
900
2
800
4
3
700
600
5
500
6
400
7
300
La solución matemática es:
VF = 1.000(1 + 0,1)6 + 900(1 + 0,1)5 + 800(1 + 0,1)4 + 700(1 + 0,1)3 + 600(1 + 0,1)2 + 500(1 + 0,1) + 400
VF = 8.800
35
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Como anotamos en la tabla 3, no existe en Excel una función predefinida para
este caso, por lo cual debemos construir nuestra fórmula, la cual podría hacerse
de la siguiente manera:
VF
Fórmula usada
para llevar el
flujo de
períodos
intermedios
hasta el final de
la inversión.
Fórmula usada
para llevar el
flujo del
período 0, al
periodo 1
En la celda B6 aparece la función incluida en la celda B5. Allí se calcula el VF
(hasta el periodo 1) de la inversión de mil en el periodo 0, de esta manera el
resultado obtenido queda en el mismo periodo del flujo de 1 y puede ser
sumado, lo cual se hace en la celda C6. La expresión (-C3+B5) está haciendo la
operación [-(-900)+1.100] y después lleva este resultado al período 2 al
multiplicarlo por uno mas la tasa. La fórmula que se muestra en C6 puede ser
copiada hasta n períodos, con lo cual se hace menos engorroso el cálculo. Esta
formulación además permitiría calcular el VF aun con tasas diferentes para cada
periodo.
36
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
2.2. Valor Presente (VP)
Es un ingreso o egreso en el momento en el presente, o al comienzo o inicio de
la inversión. Se puede calcular a partir de una suma futura, una serie de cuotas
uniformes o a partir de una serie de cuotas no uniformes. También se puede
trabajar con tasas de interés iguales para todos los periodos o con tasas de
interés diferentes en cada uno de estos. Es decir, antes de saber la fórmula
correcta para el cálculo se debe revisar si se cumplen o no los siguientes
supuestos:
Cálculo de
VP a partir
de:
Pagos
uniformes
Períodos
iguales
Tasa
constante
Tabla 4.
Opciones para el calculo del Valor Futuro
Una suma
futura
N.A.
SI
SI
Una suma
futura
N.A.
SI
NO
Cuotas
uniforme
SI
SI
SI
Cuotas NO
uniforme
NO
SI
SI
Cuota NO
uniforme
NO
SI
NO
Cuota NO
uniforme
NO
NO
SI
Fórmula
VF
VA
(1 + i ) n
VF
[(1 + i 1 ) * (1 + i 2 ) * ..... * (1 + i n )]
No existe
n
⎡ (1 + i ) − 1⎤
n ⎥
⎣ i (1 + i ) ⎦
PAGO1 PAGOt
PAGO n −1 PAGO n
+
+ ... +
+
(1 + i )1 (1 + i ) 2
(1 + i )n −1 (1 + i )n
PAGO1
PAGO 2
+
+ ....
(1 + i 1 ) [(1 + i 1 ) * (1 + i 2 )]
PAGOn −1
+ ...
[(1 + i 1 ) * (1 + i 2 ) * ....(1 + i n −1 )]
PAGOn
[(1 + i 1 ) * (1 + i 2 ) * ....(1 + i n −1 ) + (1 + i n )]
PAGO * ⎢
Función en
Excel
VA
VNA
No existe
VNA.NO.PER
N.A.: No aplica
37
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Cálculo de VP a partir de una suma futura
Su fórmula matemática es:
VP =
VF
(1 + i ) n
Ejemplo 2.5
¿Cuánto tendrá que ahorrar hoy Cesar Augusto, si necesita recibir $2.000.000
dentro de un año, si en su entidad le pagan una tasa del 2% mensual?.
El diagrama de flujo de caja del problema es:
$2.000.000
i=2%
0
12
VA=?
El planteamiento matemático del problema es:
VP =
2.000.000
= 1.402.759,72
(1 + 2%)12
Ahora resolvamos el problema usando Microsoft Excel. La función en Excel es
VA, y como ya explicamos en el numeral 2.1 paso a paso el procedimiento para
el uso de las funciones de Excel, mostraremos la solución de manera resumida:
38
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Cálculo de VP a partir de una suma futura con tasa no constante.
Este caso ocurre cuando la tasa proyectada para cada periodo es diferente. En
realidad esta en nuestra opinión es la mas común de las situaciones en la vida
práctica, pues los componentes de la tasa de interés la tasa de interés cambian
constantemente y por supuesto esta con ellos.
Su fórmula matemática es:
39
Matemáticas Financieras
PUJ
VP =
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
VF
[(1 + i 1 ) * (1 + i 2 ) * ..... * (1 + i n )]
Ejemplo 2.6
Gladys Marina de las Mercedes es una madre de familia muy preocupada por la
educación de su hija Laura Catalina. Ha estado pensando en empezar a
asegurar su educación ahorrando una suma que alcance a pagar el valor de la
matricula del primer semestre de Universidad, el cual ella estima estar alrededor
de los 15 millones de pesos en 5 años.
Como es una persona muy bien
informada de la situación del mercado de capitales, considera que las tasas de
interés para los próximos cinco años se comportarán de la siguiente manera:
Año
1
2
3
4
5
Tasa
12%
12,5%
13%
14%
10%
El diagrama de flujo de caja del problema es:
15.000.000
12% 12,5% 13% 14% 10%
VP=?
El planteamiento matemático del problema es:
15.000.000
[(1 + 0,12) * (1 + 0,125) * (1 + 0,13) * (1 + 0,14) * (1 + 0,1)]
VP = 8.401.266
VP =
40
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
En Excel no existe una función que resuelva el problema directamente, así que
es necesario hacer una solución paso por paso. Observe que el denominador de
la fórmula es la productoria de las tasas de interés sumadas con uno, esto
significa que el primer paso podría ser sumar uno a cada una de las tasas de
interés:
Ahora, para terminar el denominador de la función debemos multiplicar los
factores, esto se puede hacer con la función “PRODUCTO”, en esta función
seleccionamos en “Número1” todo el rango de valores a multiplicar:
41
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
B4:F4
Ya completado el denominador, simplemente se tiene que dividir la suma futura
entre el resultado arrojado en el denominador.
=B1/B5
Cálculo de VP a partir de una serie de cuotas uniformes.
Recordemos que las cuotas uniformes son una serie de flujos de caja
exactamente iguales durante todos y cada uno de los periodos de la inversión.
Su fórmula matemática es:
42
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
⎡ (1 + i )n − 1⎤
VP = PAGO * ⎢
n ⎥
⎣ i (1 + i ) ⎦
Ejemplo 2.7
Erasmo, un ingeniero contratista, sabe que los gastos mensuales de su familia
ascienden a $2.800.000. Como acaba de ganar una licitación, quiere conocer
cuál es el valor que debe consignar hoy en el banco “Megalómano” para cubrir
los egresos familiares durante 6 meses. “Megalómano” paga una tasa de interés
del 0,8% mensual.
El diagrama de flujo de caja del problema es:
2.800.000
0
1
3
2
4
5
6
VP=?
El planteamiento matemático del problema es:
⎡ (1 + 0,008) 6 − 1⎤
6 ⎥
⎣ i (1 + 0,008) ⎦
VP = 2.800.000 * ⎢
VP = 16.339.457
En Excel el problema se resuelve de nuevo con la función VA:
43
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Cálculo de VP a partir de una serie de cuotas no uniformes
Las cuotas no uniformes son una serie de pagos en los periodos intermedios, en
los que los montos difieren en alguno o todos los periodos. Su fórmula
matemática es:
VP =
PAGO1 PAGOt
PAGO n −1 PAGO n
+
+ ... +
+
(1 + i )1 (1 + i ) 2
(1 + i )n −1 (1 + i )n
44
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Ejemplo 2.8
A Juan Felipe le han ofrecido que le entregan cuando se pensione ciertos
montos para su subsistencia, Juanita, analista de WF le ha explicado que las
personas requieren de mayores ingresos cuando recien se pensionan y van
bajando a medida que envejecen, por eso, WF ha diseñado un plan pensional
que cubre estas necesidades.
A Juan Felipe le ha enviado el siguiente cuadro que muestra los pagos que le
realizarán en cada uno de los períodos. Si tiene una tasa de descuento del 15%
anual. ¿Cuánto sería lo máximo que debería invertir en el plan pensional?.
Año
1
2
3
4
Flujo
0
0
0
0
5
6
7
8
9
10
100 95
90
85
80
75
100
0
1
2
3
4
95
5
6
90
7
85
80
8
9
75
10
VP=?
El diagrama de Flujo de Caja del problema sería:
La solución matemática es:
VP =
100
95
90
85
80
75
+
+
+
+
+
(1 + 0,15) 5 (1 + 0,15) 6 (1 + 0,15) 7 (1 + 0,15) 8 (1 + 0,15) 9 (1 + 0,15)10
Para la solución en Excel se debe utilizar la función VNA, que trae a valor
presente cuotas no uniformes y se usa de la siguiente manera:
45
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
La función, aplicada en la celda B4, requiere la tasa de descuento (tasa) y el
rango de valores desde el período 1 hasta el último, subrayamos que es desde
el periodo 1 y no se puede incluir dentro del rango valores ubicados en el
período cero, pues calcularía el valor presente del período (-1). Otra
característica de esta fórmula es que se pueden meter los valores uno a uno,
caso en el cual la función creará casillas para incluir más cuotas, o se puede
incluir un rango de fila o columna tal como lo hicimos aquí.
Debemos anotar también que se debe tener sumo cuidado con los rangos
intermedios en donde no existe flujo de caja (en este caso los periodos 1 al 4 en
donde no existen ni ingresos ni egresos), en estos se debe poner cero, de lo
contrario Excel asumirá que no existe el periodo. Observe el resultado que
mostramos en el siguiente gráfico en donde hemos eliminado los ceros de los
períodos 1 al 4.
46
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Observe que el resultado de la fórmula cambió, el resultado ahora es
exactamente el mismo que si lleva las cuotas del periodo 5 en adelante, al
periodo 4.
Cálculo de VP a partir de una serie de cuotas no uniformes y tasa no
constante
VP =
PAGO 1
PAGO 2
PAGO n −1
PAGO n
+
+ .... +
+
[(1 + i 1 ) * (1 + i 2 ) * ....(1 + i n −1 )] [(1 + i 1 ) * (1 + i 2 ) * ....(1 + i n −1 ) + (1 + i n )]
(1 + i 1 ) [(1 + i 1 ) * (1 + i 2 )]
En muchas ocasiones, principalmente cuando se hace evaluación financiera de
proyectos, se deben calcular valores actuales con estas características, esto
supone un problema en la cantidad de cálculos necesarios, el cual trataremos de
simplificar usando la hoja de cálculo.
Ejemplo 2.9
La compañía FANATER está pensando en comprar un nuevo microbús, el cual
ofrece los ingresos que se muestran a continuación. FANATER, considera que
su tasa de descuento aumentará en los próximos años como resultado del
incremento del rendimiento de los títulos del tesoro de los Estados Unidos, y se
comportará de la siguiente manera:
Año
1
2
3
4
Ingresos
300
400
500
600
Tasa
15%
16%
18%
20%
FANATER quiere conocer a cuánto equivalen sus ingresos en términos de
valor actual.
47
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
El diagrama de Flujo de Caja del problema sería:
600
VP=?
400
500
300
15% 16% 18% 20%
La solución matemática es:
300
400
500
600
+
+
+
(1 + 0,15) [(1 + 0,15) * (1 + 0,16)] [(1 + 0,15) * (1 + 0,16) * (1 + 0,18)] [(1 + 0,15) * (1 + 0,16) * (1 + 0,18) * (1 + 0,2)]
VP = 1.196
VP =
Aunque Excel no tiene una función específica para este problema, si se puede
simplificar el cálculo reexpresando la fórmula de la siguiente manera:
600
(1 + 0,2)
400 +
(1 + 0,18)
300 +
(1 + 0,16)
VP =
(1 + 0,15)
500 +
Con esta reexpresión de la fórmula lo que hacemos es empezar a resolver la
ecuación desde los periodos más cercanos, hasta los mas cercanos a cero, esto
en Excel significa que se construye la fórmula en el último período y se copia
hasta el cero de la siguiente manera.
Observe que en la celda E4 se ha construido una fórmula cuyo numerador suma
lo que “viene” de los periodos posteriores (F4) más el flujo del año, y en el
48
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
denominador lo descuenta a la tasa del año. Cuando se copia esta fórmula para
los periodos anteriores (1 al 3) se va logrando el efecto acumulativo que
buscábamos, de forma que la fórmula calculada en el periodo uno, obtiene
Solución
realmente el valor presente del periodo cero.
49
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
2.3. Ejercicios
1. Juan acaba de ganar una demanda por incumplimiento de un contrato
de construcción por parte de la ciudad. El valor del contrato hace 18
meses era de $158.000 y el juez determino que se le deben reconocer
intereses del 2% mensual. ¿Cuánto deberá reclamar Juan que le
paguen en la tesorería distrital?.
2. ¿Cuánto tendrá que ahorrar hoy Clarita, si necesita recibir $2.000.000
dentro de un año, si en su entidad le pagan una tasa del 2%
mensual?.
3. ¿Cuál es el valor futuro de un ahorro de $130, hecho en una entidad
que paga las siguientes tasas de interés:
Periodo 1 Periodo 2 Periodo 3 Periodo 4 Periodo 5 Periodo 6
10%
12%
16%
13%
18%
11%
4. Don Pepe quiere comprar un apartamento pero no tiene la cuota
inicial, así que planea abrir con su salario del próximo mes una cuenta
en el banco para ahorrar en cada uno de los próximos 36 meses una
cuota de $200.000. ¿De cuánto podrá ser valor de la cuota inicial, si la
tasa de interés que ofrece el banco es del 1,5% mensual?.
5. ¿En cuánto se debe comprar un bono cero cupón, con valor nominal
de $1.000, con plazo de tres años, si se quiere tener una rentabilidad
del 10% anual?
6. A Maria Teresa le acaban de ofrecer que le pagan hoy las 6 cuotas de
$100.000 que le deben. Si la tasa de interés a la cual fue pactado el
préstamo es del 1% mensual ¿Cuánto le deben pagar?.
50
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
7. Ivan Darío esta estudiando la posibilidad de comprar con sus amigos
un carro de perros calientes. Este negocio puede producir utilidades
por $100.000 en el primer mes, $120.000 en el segundo mes,
$180.000 en el tercer mes, $200.000 en el cuarto mes. Como él tiene
su dinero invertido en un CDT que le paga el 0,5% mensual, quisiera
saber a cuanto equivaldrían hoy estos flujos mensuales.
8. ¿Cuánto se deberá pagar por un bono cuyo valor de emisión fue de
100 y que paga un cupón del 15% anual durante 6 años, si se quiere
obtener una rentabilidad del 12% anual? ¿si se desea una rentabilidad
del 18% anual?.¿Cuánto sería el descuento en cada uno de los dos
casos?
51
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
3. Tasas Equivalentes
Hasta ahora solo hemos estudiado casos donde el flujo de dinero encaja
correctamente con el período en el que esta expresada la tasa. Sin embargo en
muchas ocasiones las tasas y los flujos de dinero no coinciden, por ejemplo,
cuando vamos a abrir un CDT a 3 meses, nos informan la tasa que nos pagarían
si invirtiéramos a un año. En estos casos es necesario poder manipular las tasas
para saber cuanto nos van a dar realmente. No sobra mencionar que la tasa que
nos pagarán no es simplemente la anual dividida entre cuatro. Más adelante
explicaremos esto con mayor detenimiento.
3.1. Intereses anticipados y vencidos
Los intereses se pueden pagar al comienzo o al final del periodo, aunque
internacionalmente no es muy común que se paguen de la primera forma, en
Colombia, se usan continuamente los dos formatos.
El interés anticipado se ocasiona cuando los intereses se pagan al comienzo del
periodo.
I
VA
VA
Por su parte, el interés vencido se ocasiona con el pago de intereses al final del
periodo.
52
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
I
VA
VA
Para entender la relación entre estos dos tipos de interés recurriremos a un
ejemplo sencillo:
Ejemplo 3.1
A alguna empresa le acaban de pagar una factura por $400.000 con un cheque
posfechado a un mes. Como la empresa necesita urgentemente el dinero,
decide recurrir a los servicios de un prestamista que entre sus actividades tiene
el cambio de cheques posfechados.
El prestamista, gustosamente cambia el cheque y le entrega a Agricol $380.000,
pues cobró los intereses (5%)
por adelantado. ¿Cuál es el costo de este
crédito?
A primera vista, podríamos decir que fue del 5%, sin embargo, detengámonos un
poco más en el problema. El diagrama de flujo de caja del prestamista es:
$400.000
0
1
$380.000
Este señor invierte 380.000 para ganar dentro de un mes 400.000, si calculamos
la tasa de interés, retomando la fórmula (1)
53
Matemáticas Financieras
PUJ
i =
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
400.000
VF
−1=
− 1 = 0 ,0526
380.000
VA
ó
5,26%
¿Qué paso con el 5% del que habíamos estado hablando?
Cuando trabajamos con interés anticipado hay una disminución de la inversión,
por lo que la rentabilidad de la inversión aumenta. Observe que si hubiésemos
hecho el mismo ejercicio pero con una inversión de 400.000 y un ingreso de
420.000 la rentabilidad hubiese sido del 5%, pero al disminuir la base del cálculo
de 400.000 a 380.000, los intereses de 20.000 pasan a ser el 5,26% de la
inversión. Lo anterior nos muestra que hay una relación entre el interés
anticipado y el interés vencido. Es decir un 5,00% anticipado es equivalente a un
5,26% vencido. Matemáticamente podríamos decir que:
iv =
ia
1 − ia
=
0,05
= 0,0526
1 − 0,05
De manera análoga podremos decir que:
ia =
iv
1 + iv
=
0,0526
= 0,05
1 + 0,0526
Por último queremos señalar que la rentabilidad o tasa de interés del ejercicio
3.1 es 5,26%, nunca 5%. De hecho, el interés anticipado tiene un problema
conceptual, recordemos que una inversión es “un sacrificio de recursos hoy, con
la esperanza de recibir un beneficio en el futuro”. Si nos detenemos a pensar el
momento en el que se pagan los intereses, no tiene mucho sentido que me
entreguen beneficios hoy, pues acordémonos que habíamos dicho que el dinero
solo tiene sentido como recurso cuando se puede tener por periodo de tiempo, y
en el caso de los intereses anticipados, estos se pagan antes de tenerlos un
54
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
tiempo, con lo cual se genera una contradicción, por eso hecho su uso es cada
vez más escaso.
Ejemplo 3.2
Una compañía de Leasing a empezado a comercializar su nuevo producto
“Supercarro”. Con este producto, la persona recibe un vehículo sin cuota inicial,
y paga un arrendamiento mensual anticipado, cuyo costo será del 1% mensual.
Calcule el costo del crédito en términos vencidos.
El costo sería de: _____________ mensual vencido.
3.2. Tasas nominales y efectivas
La diferencia entre las tasas efectivas y nominales, surge cuando se pacta una
tasa de interés para un periodo de tiempo determinado (Ej. Años) pero los
intereses se liquidan en lapsos de tiempo mas cortos (ej. Meses). La tasa de
interés nominal se ocasiona cuando los periodos de pago de intereses son
fracciones del periodo para el cual se ha pactado la tasa. Las tasas de interés
efectivas son el reconocimiento a la capitalización de intereses que ocasiona
una tasa de interés nominal.
Explicaremos esto con un ejemplo sencillo:
55
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Ejemplo 3.3
La señora Pepita tiene $1.000.000 para invertir por un año.por lo cual ha
llamado a su asesor de la entidad financiera “Megalómano”, y este le ha
ofrecido dos opciones:
Opción uno: Invertir en un CDT a un año, con una tasa del 24.63% anual, en
el cual que le paga intereses cada trimestre vencido.
Opción dos: Invertir el millón en un CDT a un año con una tasa del 24.14%
anual, que le paga el intereses cada mes vencido.
¿Cuál de las dos opciones debe escoger doña Pepita?
Primero observemos los diagramas de flujo de caja de las dos opciones:
1.000.000
24,63%
= 6,16% * 1.000.000 = 61.576
4
61.576
61.576
61.576
1
2
3
61.576
Opción 1:
4
i = 24,63% anual
1.000.000
1.000.000
24.14%
= 2,01% * 1.000.000 = 20.118
12
20.118
Opción 2:
1
2
i = 24,14% anual
1.000.000
56
3
4
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Observe que los dos flujos no son comparables porque cada uno tiene pagos en
diferentes períodos de tiempo. Entonces ¿qué podemos hacer?. Una alternativa
sería, dado que los dos flujos son a un año, suponer que la señora no recibe los
intereses en ninguno de los trimestres o meses y por lo tanto los intereses
quedarían “capitalizados” a la misma tasa a la que inicialmente fue puesto el
dinero. Es decir, todos los flujos serían llevados a VF a la tasa pactada
inicialmente:
73.665
VF = 61.576 * (1 + 6,16%)3
VF = 61.576 * (1 + 6,16%)2
VF = 61.576 * (1 + 6,16%)
69.392
65.367
61.576
270.000
1.000.000
61.576
61.576
61.576
1
2
3
1.000.000
4
Como puede observar cambiamos un flujo que estaba partido a la mitad, por uno
en el que solamente hay una inversión y un ingreso al final del año.
1.270.000
1
1.000.000
57
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Si calculamos la rentabilidad que podría obtener la señora al final del año,
siempre y cuando capitalice todos los ingresos hasta el final de la vida del CDT y
que “Megalómano” sostenga siempre la misma tasa de interés para la
reinversión de intereses, sería:
i =
VF
1.270.000
−1=
− 1 = 0 , 27
VA
1.000.000
ó
27%
Hagamos ahora lo mismo con la opción dos:
Si doña Pepita reinvirtiera todos los intereses a la tasa pactada inicialmente, las
dos opciones serían iguales.
En este ejemplo manejamos tres tipos de tasas que son para la opción 1:
•
24,63%. Esta tasa es una nominal
•
6,16%. Que es una tasa periódica
•
27%. Es la tasa Efectiva.
Estudiemos ahora estos tres tipos de tasas:
58
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Tasa de interés efectiva
La tasa efectiva es precisamente aquella a la que se llega cuando se capitalizan
los intereses pagados a la misma tasa a la cual se pactó el negocio al comienzo
del período. Observe que por su misma definición no puede existir una tasa
efectiva anticipada, pues los intereses no estarían capitalizados en el período.
Su fórmula matemática es:
⎛
i efectivo = ⎜⎜1 +
⎝
i no min al _ vencido
n
n
⎞
⎟⎟ − 1.
⎠
O partiendo de la tasa periódica:
i efectivo = (1 + i periodico _ vencido ) − 1.
n
Calcule la tasa de interés efectiva de la inversión de doña Pepita a partir del
24,63%:
Ahora por favor calcule la efectiva a partir de la tasa periódica:
59
Eliminado: <sp>
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Tasa de interés nominal
Es una tasa pactada para un período, pero los intereses se pagan en períodos
menores al pactado en la tasa.
Su fórmula matemática es:
i no min al = n *
[ (1 + i
n
efectivo
) − 1]
O partiendo de la tasa periódica:
i no min al = i periodico * n
Nomenclatura de las tasas nominales
Una de los mayores cuidados que debemos tener cuando trabajemos con tasas
nominales es darles el nombre apropiado a cada una de ellas. Usando como
ejemplo la tasa nominal del caso anterior, podríamos decir que el 24,63% es una
tasa Nominal Anual trimestre vencido
24.63% NOMINAL
Advierte que
los periodos
de pago de
intereses son
menores que
el período en
el que se
pactó la tasa
de interés
ANUAL
Indica el
periodo al
cual fue
pactada la
tasa de
interés
60
TRIMESTRE
Se refiere
a los
períodos
de pago
de
intereses
VENCIDO
Muestra si
la forma de
pago es
anticipada
o vencida
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
En la práctica, muchas veces se omiten algunos de estos términos y
simplemente se le llama 24,63% T.V. pues se asume que si se especifica el
periodo de liquidación de intereses, la base de la tasa es un año y se trata de
una tasa nominal.
Calcule la tasa de interés nominal anual semestre vencido de la inversión de
doña Pepita a partir del 27%EA:
Ahora por favor calcule la tasa N.A.T.V. a partir del 6,11% periódico:
Tasa de interés Periódica
La tasa de interés periódica es la tasa pactada para un periodo. Es l más común
de todas, siempre que hablamos del 2% mensual, del 25% anual estamos
hablando de una tasa periódica. En nuestro concepto es la más importante de
61
Eliminado: <sp>
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
todas porque con ella se calculan los flujos de caja. Observe en el ejemplo de
Doña Pepita que el valor de los intereses fue calculado con la tasa periódica.
Su fórmula matemática es:
i periodico = n (1 + i efectivo ) − 1
O partiendo de la tasa nominal:
i periodico =
i no min al
n
Calcule la tasa de interés periódica mensual de la inversión de doña Pepita a
partir del 27%EA:
Ahora por favor calcule la tasa periódica a partir del 24,14% NAMV.
62
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Relación entre las tasas efectivas, nominales y periódicas
La utilidad de poder establecer una relación entre las diferentes tasas de interés
es poder establecer equivalencias que permitan cambiar tasas de un periodo a
otro de manera que puedan ser armonizadas con los tiempos de los flujos de
caja. Es importante que se determine la relación entre las tasas y los flujos, esta
puede ser:
La tasa determina el flujo: En este caso, la tasa explica la forma de pago de los
intereses. Por ejemplo, un bono que paga una tasa del 24%NAMV, supone que
los intereses serán pagados cada mes y de forma vencida. En este caso no se
requiere hacer ninguna conversión de la tasa.
•
La tasa no concuerda con los periodos del flujo: En algunas ocasiones
las tasas no son compatibles con el periodo del flujo y por lo tanto hay
que convertirla para que se ajuste a este. Por ejemplo en Colombia la
tasa referencia DTF es por su definición TA, y si se usa para un CDT a
un mes, se requerirá usar una tasa mensual y no trimestral.
En realidad hay muchas formas de convertir tasas, cada procedimiento se podría
hacer de muchas formas, sin embargo, nosotros aconsejamos usar una sola
Tasa.nominal
⎡ inom ⎤
⎢ n ⎥
⎣ ⎦
[i
per
* n]
Periódica
n
⎡ inom⎤
⎢⎣1+ n ⎥⎦ −1
Nominal
vencida
Efectiva
1
n * ⎡⎢(1 + ief )n − 1⎤⎥
⎣
⎦
Int.efectivo
ia =
iv
(1+iv )
iV =
ia
(1 − ia )
Anticipada
Vencida
forma de conversión que permita mecanizar un procedimiento sencillo.
Gráficamente las conversiones son las siguientes:
63
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Observemos con un ejemplo numérico cómo usar este procedimiento, al
convertir una tasa efectiva anual a una nominal anual trimestre anticipado:
n * ⎡⎢(1 + ief
⎣
27%
)
1
n
⎡ inom ⎤
⎢ n ⎥
⎣ ⎦
− 1⎤⎥
⎦
ia =
24,63%
6,16%
23,20%
[i
per * n
]
iv
(1+iv )
5,80%
Lo anterior también podría usarse de manera contraria, es decir, si nos
devolviéramos por el mismo camino podríamos buscar una tasa EA a partir de
una NATA.
Cuando se hacen estas conversiones es necesario seguir algunas reglas:
•
NUNCA divida una tasa Efectiva. Si Usted divide la tasa del 27% entre
cuatro, no logrará nunca obtener el 24,63%
•
NUNCA Multiplique una tasa de nominal: La relación entre las tasas
nominales y efectivas no son ni productos no divisiones.
•
SIEMPRE que multiplique una tasa, el resultado será una nominal
•
SIEMPRE que divida una tasa nominal el resultado será una tasa
periódica: Tenga cuidado, las tasas nominales solo se pueden dividir
entre el número de periodos de los intereses para los cuales fue
calculada. Es decir una tasa NATV solo se puede dividir entre 4 y una
tasa NASV solamente se podrá dividir entre 2.
•
NUNCA divida una tasa periódica. Si Usted desea convertir el 6,16%
trimestral en una tasa mensual no la puede dividir entre tres.
64
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
La funcionalidad de las tasas efectivas
La última regla para la conversión de las tasas proponía que no se pueden
dividir las tasas periódicas y que si se multiplican los resultados serán
nominales, entonces ¿qué hacemos cuando queremos convertir por ejemplo un
6,16% trimestral en una tasa mensual o semestral?
En estos casos se encuentra la utilidad de las tasas efectivas, estas son un
puente para cuando se decide cambiar de un periodo a otro, ellas nos permiten
pasar de una tasa trimestral a una mensual o viceversa.
Efectiva
Períodica
TV
La tasa efectiva es un “puente”
que permite cambiar tasas de un
período a otro
MV
SV
AA
TA
Una tasa efectiva nos permite entonces hacer múltiples conversiones a
diferentes tipos de periodos.
65
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
24,14% NAMV
n
24,63% NATV
n=4
=
12
n=2
27,00% E. A.
25,39% NASV
n=6
n
=
24,38% NABV
1
27,00% NAAV
Ejercicios
1. Muestre por favor cuánto dinero puede prestar realmente una persona que
tiene $1.000.000 y cobra al 3% anticipado.
Valor que
Intereses que
supuestamente
cobra por
presta
anticipado
Valor que
Valor que recibe
realmente entrega al final del mes
Totales
Calcule la rentabilidad que generó el negocio
66
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
En otras palabras, un 3% anticipado es equivalente al ____________% vencido
2. Por favor complete el siguiente cuadro de tasas anticipadas y vencidas
equivalentes:
TASAS EQUIVALENTES
ANTICIPADAS
VENCIDAS
1,00%
DIFERENCIA
1,01
0,01%
2,00%
3,00%
4,00%
5,00%
6,00%
3. Usted invierte $10.000.000 en un CDT, a un año que le paga el 1% bimestral.
¿Cuánto tendrá al final del año, si no recoge los rendimientos, sino que mas bien
los reinvierte a la misma tasa que le ofrecieron inicialmente?
100.000
0
10.000.000
1
100.000
2
100.000
3
100.000
4
100.000
100.000
5
La rentabilidad bimensual es
Nombre técnico
10.000.000
Lo que recibiría si retirara los intereses mensuales es
Nombre técnico
10.000.000
-
TOTAL
6
ó
Cada bimestre
ó
Cada año
ó
Cada año
67
Lo que efectivamente recibió capitalizando los intereses fue
Nombre técnico
10.000.000
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
4. Una compañía de Leasing acaba de entregar un vehículo con tasa del 36%
Efectiva anual ¿A qué tasa Nominal Anual Trimestre anticipado corresponde
este crédito?
Tasa.nominal
n * ⎡⎢ (1 + ief
⎣
)
1
n
ia =
⎡ i nom ⎤
⎢ n ⎥
⎣
⎦
− 1⎤⎥
⎦
iv
(1+ iv )
36,00%
[i
per
*n
]
5. ¿A qué tasa efectiva anual corresponde una inversión que se realiza al 24%
N.M.A.?
Int.efectivon
⎡ inom ⎤
⎢⎣1 + n ⎥⎦ − 1
i per *n
24,00%
⎡ i nom ⎤
⎢ n ⎥
⎣
⎦
6. Calcule las tasas nominales equivalentes al 25% N.A.M.V.
68
iV =
ia
(1 − ia )
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
NAMV
n
25,00% NAMV
n=
E. A.
=
12
NASV
n=2
n=6
n
=
NABV
1
NAAV
Anual
vencida
Mensual
anticipada
Trimestral
anticipada
Semestral
vencida
NAAA
NAMV
NATV
NASA
EA
7. Por favor complete la siguiente tabla:
20%
18%
15%
10%
23%
5%
2%
1%
25%
69
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
4. Tablas de amortización
Las tablas de amortización describen el plan de pagos (comportamiento
mensual) de un crédito, en términos del valor adeudado, la cuota cancelada, y
su distribución entre abonos a capital e intereses.
Estas tablas son muy importantes porque muestran cómo se distribuye la cuota,
que parte de esta se dedica al pago de intereses y cual se constituye como
amortización de capital. Adicionalmente se puede observar en ellas cómo se va
disminuyendo el monto adeudado hasta que llega a cero.
4.1. Componentes de una tabla de amortización.
Saldo Inicial: Es el valor adeudado al comienzo del período. En el primer
período es el valor del crédito y de allí en adelante es el mismo saldo final del
período anterior.
Intereses: Son el costo que se paga por tener el capital en el periodo. O en
otras palabras, lo que cobra el banco por prestar el dinero. Se calcula
multiplicando el saldo4 del crédito por la tasa de interés.
Abono a capital: Es el monto en el que se disminuye la deuda.
Cuota: Es el valor total que se paga, incluidos tanto los intereses como el abono
a capital.
Saldo final: Es el saldo del crédito después de haber aplicado la cuota. Se
calcula como el saldo inicial menos el abono de capital.
4
Será el saldo inicial cuando se trate de pagos vencidos y el saldo final cuando se trabajen
pagos anticipados.
70
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
4.2. Tipos de tablas de amortización
Observe por favor que en el numeral anterior no se definió la forma de cálculo ni
de los abonos a capital ni de las cuotas. Esto se debe estos cambiarán
dependiendo de la forma de amortización elegida. Se podría decir en general
que hay dos formas básicas de pagar un crédito: Cuando se decide el monto de
la cuota y cuando se decide el monto del abono a capital.
DOS FORMAS DE DEFINIR EL
PAGO DE CREDITOS
Se decide el monto de
la CUOTA o PAGO
Se decide el monto
del Abono a Capital
4.3. Tablas de amortización cuando se define la cuota
En este caso se decide sobre el monto total a pagar, como consecuencia lo que
se abona a capital será simplemente la diferencia entre el valor pagado y los
intereses. En este esquema se pueden determinar cuotas uniformes o cuotas
variables.
En general la estructura de una tabla de amortización cuando se define la Cuota
es:
Periodo
Saldo inicial
Abono a
capital
Intereses
No existe
Cuota
0
No existe
No existe
1
Saldo final
del periodo
anterior
Saldo inicial
Depende si
Cuota menos
por la tasa de
es fija o
intereses
interés
variable.
71
No existe
Saldo final
Valor del
crédito
Saldo inicial
menos abono
a capital
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Tablas de amortización con cuota fija
Esta es una de las formas más comunes de liquidación de los créditos, consiste
en que se paga una suma fija durante todos los periodos de duración del crédito.
Para calcular la cuota uniforme se utiliza la siguiente fórmula:
PAGO = VA
i (1 + i ) n
(1 + i ) n − 1
La tabla de amortización queda diseñada de la siguiente manera:
Periodo
Saldo inicial
Abono a
capital
Intereses
0
No existe
No existe
No existe
1
Saldo final
del periodo
anterior
Saldo inicial
Cuota menos
por la tasa de
intereses
interés
Cuota
No existe
PAGO = VA
i (1 + i ) n
(1 + i ) n − 1
Saldo final
Valor del
crédito
Saldo inicial
menos abono
a capital
Ejemplo 4.1
Una persona ha pagado una compra de un millón de pesos con tarjeta de
crédito, y ha diferido el pago a 6 cuotas. Sabiendo que la entidad financiera
cobra intereses del 1% mensual, Calcule el valor de la cota mensual y la tabla
de amortización de este crédito.
El diagrama de flujo de caja del problema es:
1.000.000
0
1
2
3
4
5
6
CUOTA = ?
72
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
El valor de la cuota mensual se calcula de la siguiente manera:
PAGO = 1.000.000
0,01(1 + 0,01) 6
= 172.548,37
(1 + 0,01) 6 − 1
En Excel debemos usar la función PAGO.
La tabla de amortización del crédito es:
Periodo
Saldo inicial
Intereses
Abono a
capital
Cuota
0
Saldo final
1.000.000
1
1.000.000
10.000
162.548
172.548
837.452
2
837.452
8.375
164.174
172.548
673.278
3
673.278
6.733
165.816
172.548
507.462
4
507.462
5.075
167.474
172.548
339.988
5
339.988
3.400
169.148
172.548
170.840
6
170.840
1.708
170.840
172.548
0
73
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Para construir la tabla de amortización en Excel debe primero armar el
encabezado de la tabla y el número de períodos.
Cuando las tablas de amortización tienen muchos periodos, es necesario usar
herramientas para poder poner rápidamente el número de los periodos, por lo
que se debe señalar la celda donde esta el periodo 0, y después arrastrarla con
el “ratón”, tomándola del cuadro que aparece en el borde inferior derecho de la
celda y oprimiendo siempre al mismo tiempo la tecla “Control”, si se hace de
manera correcta aparecerá a medida que va arrastrando el número que quedará
en la celda. Cuando llegue al último periodo suelte primero el botón del “ratón” y
después la tecla “Control”.
74
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Este pequeño signo de adición
aparecerá siempre que tenga
oprimida la tecla “Control”
Número del período
Después se construye la primera línea de la tabla, debe tener cuidado con
aquellas celdas que son fijas, tal como se muestra en el siguiente gráfico:
75
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Después se selecciona toda la fila desde el saldo inicial hasta el saldo final y se
copian las fórmulas oprimiendo doble clic en el cuadro inferior derecho de la
selección:
Ejemplo 4.2
Una persona acaba de solicitar un préstamo por $200.000 a 6 meses a una tasa
de interés mensual del 2%. Calcule el valor de la cota mensual y la tabla de
amortización de este crédito.
La cuota sería de:
76
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Eliminado: <sp>
El diagrama de flujo de caja del problema sería:
0
1
2
3
77
4
5
6
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Y la tabla de amortización del crédito quedaría de la siguiente manera:
Periodo
Saldo inicial
Intereses
Abono a
capital
Cuota
0
Saldo final
200.000
1
2
3
4
5
6
Tablas de amortización de cuota fija cuando se tienen tasas variables
Como mencionamos anteriormente, la tasa de interés varía a través del tiempo,
esto supone un riesgo que debe ser asumido por alguna de las dos partes. Cada
vez más, quien asume el riesgo es el que recibe el crédito. Esto supone en
principio que la cuota no puede ser constante, pues para ello se tendrían que
conocer con exactitud las tasas futuras. Sin embargo, se pueden construir tablas
de amortización con cuotas fijas hasta el penúltimo período, ajustando el error
acumulado en el último período.
Ejemplo 4.3
Se compró un carro con un préstamo de $1.000.000 a
6 meses. La tasa de interés al inicio del crédito fue del
1%, pero, debido al mayor endeudamiento del gobierno,
a tenido una tendencia alcista y se ha comportado
como se muestra en la tabla. Construya la tabla de
amortización del crédito
78
Periodo
1
2
3
4
5
6
Tasa
1,00%
1,10%
1,20%
1,30%
1,40%
1,50%
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Para construir esta tabla, en primer lugar debemos calcular la cuota uniforme
que se usará desde la primera hasta la penúltima cuota, esta se calcula con la
tasa de interés del primer periodo. En este caso es de $172.548. Después se
construye la tabla normalmente desde el periodo 1 hasta el penúltimo periodo
construir la tabla de la misma manera que lo hicimos anteriormente, la única
diferencia es que los intereses no serán multiplicados por una tasa fija, sino por
la tasa de interés de cada periodo, como se muestra en los siguientes cuadros:
674.115*0,012
El último período, el abono a capital será igual al saldo final del penúltimo
período y el cálculo de la se redefine como los intereses más el abono a capital.
Abono
a capital más intereses
79
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
En el segundo caso la persona define cuanto será lo que abona a capital, y la
cuota será entonces la suma de lo que se decidió pagar
Ejemplo 4.4
Alguien
está necesitando
un
préstamo
de
$200.000 para salir de vacaciones. En el banco
le han dicho que le prestan a una tasa de DTF +
3% durante 6 meses con cuotas uniformes
durante los 6 primeros meses y una última cuota
de ajuste. Construya por favor la tabla de
Proyección de la DTF (T.A.)
Periodo
Tasa
1
10,00%
2
10,50%
3
11,00%
4
11,50%
5
10,40%
6
10,50%
amortización del problema.
Cálculo de la tasa de interés periódica
Periodo
DTF T.A.
1
2
3
4
5
6
10,00%
10,50%
11,00%
11,50%
10,40%
10,50%
Puntos
adicionales
3%
3%
3%
3%
3%
3%
Tasa T.A.
La cuota sería de:
80
Tasa E.A.
Tasa M.V.
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Y la tabla de amortización quedaría de la siguiente manera:
Periodo
Saldo inicial
Intereses
Abono a
capital
Cuota
0
Saldo final
200.000
1
2
3
4
5
6
Tablas de amortización de cuota ascendente o descendente
Hasta hace algún tiempo, el manejo de las cuotas crecientes y decrecientes era
bastante complejo dada la gran cantidad de funciones de gradientes (factores
constantes de variación) que existían. Con la introducción de las hojas de
cálculo esta dificultad quedó superada.
La herramienta “Buscar objetivo” de Excel ayuda a construir casi cualquier forma
de tabla de amortización, observemos como funciona:
Ejemplo 4.5
Se debe construir una tabla de amortización de un préstamo por $100.000, a 12
meses de plazo y con una tasa de interés del 2% mensual, en donde la cuota
mensual se debe reajustar en un 5% cada mes.
Primero se debe construir una tabla de amortización común y corriente, con la
única diferencia que el valor de la cuota, no se ha calculado con la función
81
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
“PAGO”, sino que simplemente se escribe cualquier valor. En este caso hemos
escrito 100, pero hubiese podido escribir 55, 2.000 o simplemente dejarla en
=F53
=E54-D54
=B54*2%
Cualquier
valor
=B54-C54
blanco.
Observe que también creamos una columna donde aparecen los aumentos
(fíjese que esto implica que podríamos tener un aumento diferente para cada
período.
Después copiamos las fórmulas construidas en todas las columnas exceptuando
la de la cuota. Para fijar el valor de la segunda cuota, se debe tener en cuenta
que esta debe ser un 5% superior que la primera, esto, en términos matemáticos
se puede expresar como Cuota2=Cuota1*(1+5%), la tercera cuota debe tener el
mismo comportamiento y así sucesivamente, en general podíamos decir que
Cuotan=Cuotan-1*(1+5%). Se construye entonces la fórmula en Excel y se copia
para todo el resto de periodos.
82
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Esta fórmula,
construida en el
periodo 2 y copiada
hasta el periodo 12,
nos garantiza un
aumento del 5% en
el valor de la cuota.
El valor del saldo final del
último periodo debe ser igual
a cero.
Observe que el saldo final del periodo 12 es positivo, eso significa que todavía
no se ha terminado de pagar el capital. Si por el contrario, este valor fuese
negativo, significaría que hemos pagado más de lo que adeudábamos. También
se puede encontrar que los abonos a capital son negativos, esto sucede porque
lo que se está pagando como cuota no alcanza siquiera a cubrir los intereses, y
con el sistema de interés compuesto, la parte que queda sin cubrir se va
capitalizando y aumentando el saldo final.
EL siguiente paso entonces es encontrar un valor de la primera cuota que haga
que el saldo final del período 12 sea cero. Este es un procedimiento que Excel
puede hacer muy rápidamente con la función “Buscar objetivo”. Nuestro objetivo
83
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
es que la celda F65 (argumento: Definir la celda) sea cero (argumento: Con el
valor) , y para lograrlo debemos modificar la celda E54 (argumento: Para
cambiar la celda).
Al aceptar, Buscar objetivo resolverá el problema iterando hasta que se hallan
satisfecho satisfecho las condiciones. Después de encontrar la solución, la
función mostrará un cuadro de dialogo que anuncia que se ha encontrado una
solución.
84
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
4.4. Tablas de amortización con abono a capital uniforme
En este caso se decide sobre el valor en el que se disminuye el capital, es decir,
se determina cuanto será el abono a capital y por lo tanto el valor de la cuota
será simplemente la sumatoria del abono a capital y los intereses. En este
esquema no se pueden determinar cuotas uniformes sino que estas serán
variables. Por otro lado se podrá determinar si se hacen abonos a capital fijos o
variables.
En general la estructura de una tabla de amortización cuando se define la Cuota
es:
Periodo
Saldo inicial
Abono a
capital
Intereses
0
No existe
No existe
No existe
1
Saldo final
del periodo
anterior
Saldo inicial Depende si
por la tasa de es fijo o
interés
variable.
85
Cuota
No existe
Saldo final
Valor del
crédito
Intereses mas Saldo inicial
abono a
menos abono
capital
a capital
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Tablas de amortización con abono a capital uniforme
En este caso se busca disminuir el monto adeudado en partes iguales durante
cada uno de los periodos de pago del crédito. Para calcular el monto del abono
se utiliza la siguiente fórmula:
ABONO =
VA
n
La tabla de amortización queda diseñada de la siguiente manera:
Periodo
Saldo inicial
Abono a
capital
Intereses
No existe
Cuota
No existe
Saldo final
Valor del
crédito
0
No existe
No existe
1
Saldo final
del periodo
anterior
Saldo inicial ABONO = VA Intereses mas Saldo inicial
n abono a
por la tasa de
menos abono
interés
capital
a capital
Ejemplo 4.6
Una persona ha solicitado un seiscientos mil pesos a su fondo de empleados, el
cual será cancelado en 6 cuotas con abonos a capital uniforme, a una tasa de
interés del 1% mensual, Calcule el valor de cada uno de los pagos mensuales.
El valor del abono constante será de ABONO =
600.000
= 50.000
12
Y la tabla de amortización quedará construida de la siguiente manera:
Período Saldo Inicial
Abonos
Intereses
Cuota
0
Saldo Final
600.000
1
600.000
50.000
6.000
56.000
550.000
2
550.000
50.000
5.500
55.500
500.000
3
500.000
50.000
5.000
55.000
450.000
4
450.000
50.000
4.500
54.500
400.000
5
400.000
50.000
4.000
54.000
350.000
86
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
6
350.000
50.000
3.500
53.500
300.000
7
300.000
50.000
3.000
53.000
250.000
8
250.000
50.000
2.500
52.500
200.000
9
200.000
50.000
2.000
52.000
150.000
10
150.000
50.000
1.500
51.500
100.000
11
100.000
50.000
1.000
51.000
50.000
12
50.000
50.000
500
50.500
-
Siguiendo los mismos pasos mostrados en la sección “Tablas de amortización
con cuota fija”, la formulación del primer periodo en Excel quedaría:
Los abonos a capital también pueden ser ascendentes o descendentes, sin
embargo su construcción es igual a cuando se trata de cuotas uniformes, de
manera que lo invitamos a consultar la sección “Tablas de amortización de cuota
ascendente o descendente”
87
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Ejemplo 4.7
Una persona ha solicitado un $1.200.000 mil pesos a su fondo de empleados, el
cual será cancelado en 6 cuotas con abonos a capital uniforme, a una tasa de
interés del 1% mensual, Calcule el valor de cada uno de los pagos mensuales.
El valor del abono uniforme sería de:
Y la tabla de amortización del crédito quedaría de la siguiente manera:
Periodo
Saldo inicial
Intereses
Abono a
capital
0
Cuota
Saldo final
1.200.000
1
2
3
4
5
6
88
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
5. Ejercicios Integradores
1. ¿Cuánto se debe pagar por un bono que fué emitido hace 3 años y
medio, con un valor facial de $1.000.000, con vencimiento a cinco años,
que paga una tasa del 10% TV, si quiero que mi rentabilidad sea del 30%
EA?
2. Si una empresa recibe un crédito por $ 50.000.000 y realiza los siguientes
pagos trimestrales:
Trimestre 1 $ 5.000.000
Trimestre 2 $ 10.000.000
Trimestre 3 $ 15.000.000
Trimestre 4 y 5 $ 20.000.000
¿Cuál es la tasa efectiva anual que está pagando?
3. ACME S.A. ha emitido bonos de deuda a descuento, cuya rentabilidad es
del 25% anual. ¿Cuánto se tendrá que pagar si el título tiene un valor
facial de $1.000 y se redime en 180 días?
4. Don Pedro desea comprar una casa que vale $200 millones, de los cuales
pagará el 20% en un cuota inicial y el 80% lo obtendrá de un crédito
bancario a siete años, a una tasa del 2% mensual. Don Pedro considera
que la casa es muy grande, y piensa alquilar el primer piso de su nuevo
hogar, para pagar con el arrendamiento el 50% de la cuota. Don Pedro
recibirá el alquiler el primer día del mes, y lo colocará en una cuenta de
ahorros que paga intereses del 15% anual. ¿Cuánto debe cobrar Don
Pedro de arrendamiento?
5. Usted adquiere un vehículo que tiene un valor de $12.000.000 y se le
propone el siguiente esquema de pagos a dos años:
89
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
- Cuota inicial del 30%
- 24 Cuotas uniformes mensuales
- 2 cuotas extraordinarias de $500.000 c/u en los meses 12 y 24,
adicionales a la cuota mensual.
Si el costo del crédito es del 2% mensual. ¿A cuánto ascenderán las
cuotas mensuales ?
6. Calcule el valor de las cuotas del ejercicio anterior, suponiendo que el
monto total de las cuotas 12 y 24 es de $500.000.
Una empresa debe cobrar los siguientes valores:
· $3 millones de inmediato
· $4 millones dentro de un año
· $5 millones dentro de tres años
· $2 millones dentro de cuatro años
El deudor, que desea pagar lo más pronto posible esta obligación, ofrece
el siguiente plan de pagos: $5 millones de contado y el saldo a dos años.
Calcule el saldo si la tasa de descuento de la compañía es del 16%.
7. Se desea invetir hoy (3 de marzo de 2001) en un bono que fue emitido el
3 de marzo de 2000, con las siguientes características:
- Valor nominal: $100.000
- Tasa: Prime + 5% E.A.
- Plazo: 5 años
- Amortización: Al vencimiento.
Si Ud desea comprarlo hoy, ¿Cuánto sería lo máximo que debería pagar
por ese título si su tasa de descuento es del 6% anual?. Tasa Prime
8.75%.
8. Rodrigo es el dueño de una máquina que vale $1.000.000. Le hacen dos
ofertas de compra: La primera consiste en una cuota inicial de $200.000 y
90
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
cuatro cuotas iguales cada 3 meses. La segunda consiste en una cuota
inicial de $300.000 y dos cuotas semestrales. Si su tasa de descuento es
del 24% anual mes vencido, ¿Cuáles deben ser las cuotas trimestrales y
semestrales, para que las ofertas sean equivalentes?
9. Un inversionista ha puesto $1.000 en la bolsa, el primero de agosto del
2001 y obtiene los siguientes resultados:
- 01/08/01 compra 50 acciones por $1.000
- 06/08/01 vende 20 acciones por $350
- 10/08/01 vende 10 acciones por $300
- 13/08/01 recibe dividendos por $100
- 30/08/01 vende 20 acciones por $390
Ayude por favor a este desesperado señor a saber cual fué la rentabilidad
de esta operación en términos efectivos anuales.
10. Un inversionista desea saber cual es la rentabilidad en pesos, de un bono
que tiene las siguientes características:
- Valor nominal USD1.000
- Tasa: 8%
- Vencimiento: 3 años
- Amortizaciones: Al vencimiento
- Valor de compra: 98% de su valor nominal
- Devaluación anual esperada: 10%; TRM $2.000
11. Calcular cuánto recibirá un inversionista, que invierte $200.000 a diez
años, en un título con tasa flotante, si se sabe que la tasa de captación
del banco es de 22% anual y se estima que la tasa disminuirá un 1% los
primeros 4 años, y aumentará un 0.3% durante los 6 años siguientes.
91
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
6. Glosario
Abono a capital: Es el monto en el que se disminuye la deuda.
Bono Yankee: Es un bono soberano de cualquier país, emitido en la Bolsa de
Nueva York, de tal forma hay Yankees colombianos, ecuatorianos etc.
Bono cero cupón: Bono a descuento que se vende al descuento y no tiene
cupones.
Bono Soberano: Bono emitido por el gobierno de cualquier país.
Bono5: Es la promesa de pago que hace una empresa con la cual se
compromete a pagar el valor nominal al vencimiento (maduración o redención) y
unos intereses pactados (cupones) que se pagan periódicamente. La firma los
puede vender a descuento o no (a descuento significa que los vende por menor
valor que el nominal). Así mismo, puede ofrecer intereses periódicos (cupones) o
no.
Cuota: Es el valor total que se paga, incluidos tanto los intereses como el abono
a capital.
Cuota: Se tiene una cuota o pago cuando en lugar de pagar la totalidad de la
inversión al finalizar el plazo, se entregan VARIAS sumas de dinero en
diferentes periodos de tiempo.
Cuotas no uniformes: en el caso en el que los montos entregados difieran en
algún periodo.
5
Tomado de Vélez 2004
92
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Cuotas uniformes: Son cuotas en donde se le entrega exactamente en mismo
monto durante todos y cada uno de los periodos, o
Cupón6: Talón que debe desprenderse de un título de acciones para reclamar
dividendos, recibir acciones gratuitas o solicitar nuevas acciones, o que debe
desprenderse de un bono al portador para cobrar intereses. Orden presentada
para obtener un pago monetario, mercancía o servicio.
DTF (Depósito a término Fijo): Es el promedio semanal de la tasa de captación
de los certificados de depósito a término (CDTs) a 90 días emitidos por las
entidades de crédito, calculado por la Superintendencia Bancaria.
Intereses: Son el costo que se paga por tener el capital en el periodo. O en
otras palabras, lo que cobra el banco por prestar el dinero. Se calcula
multiplicando el saldo7 del crédito por la tasa de interés.
Número de periodos (n): Es el tiempo que dura inversión, desde que se inicia
hasta que se termina. También se puede interpretar como el número de periodos
que separan los valores en el tiempo y a su vez permiten hacer las
transformaciones.
Pago: Se tiene una cuota o pago cuando en lugar de pagar la totalidad de la
inversión al finalizar el plazo, se entregan
VARIAS sumas de dinero en
diferentes periodos de tiempo. En EXCEL pago se entiende como una suma
uniforme que se entrega en todos y cada uno de los periodos en los que esta
compuesta la inversión.
6
Tomado del diccionario de términos de la Superintendecia de Valores
Será el saldo inicial cuando se trate de pagos vencidos y el saldo final cuando se trabajen
pagos anticipados.
7
93
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Saldo final: Es el saldo del crédito después de haber aplicado la cuota. Se
calcula como el saldo inicial menos el abono de capital.
Saldo Inicial: Es el valor adeudado al comienzo del período. En el primer
período es el valor del crédito y de allí en adelante es el mismo saldo final del
período anterior.
Spread: Diferencia de rentabilidad annual entre el T’Bond y un Yankee. Medida
de riesgo usada para calcular riesgo de una economía específica.
Tabla de Amortización: describe el plan de pagos (comportamiento periódico)
de un crédito, en términos del valor adeudado, la cuota cancelada, y su
distribución entre abonos a capital e intereses.
Tasa de descuento: Es la tasa que hace equivalente el consumo de hoy a un
consumo superior dentro de un periodo de tiempo. Si se le ofrece a este
inversionista una tasa menor, decidirá consumir ahora, si por el contrario, la tasa
es mayor, la persona optará por invertir”.
T-Bond (Treasury Bond): Son los Bonos del Tesoro de Estados Unidos
emitidos en la Bolsa de Nueva York. Son los equivalentes en el mercado
norteamericano de los TES del mercado colombiano. Son los títulos de menor
riesgo en el mundo.
TES (TÍTULOS DE TESORERÍA)8: Títulos de deuda pública emitidos por la
Tesorería General de la Nación (en pesos, en UVR´s - Unidades de Valor Real
Constante - o en pesos ligados a la TRM) que son subastados por el Banco de
la República. Se caracterizan por ser una de las mayores fuentes de financiación
del Gobierno.
8
Tomado del diccionario de términos de la Superintendecia de Valores
94
Matemáticas Financieras
PUJ
Valor actual:
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Es un ingreso o egreso en el momento en el presente, o al
comienzo o inicio de la inversión. Se puede calcular a partir de una suma futura,
una serie de cuotas uniformes o a partir de una serie de cuotas no uniformes.
También se puede trabajar con tasas de interés iguales para todos los periodos
o con tasas de interés diferentes en cada uno de estos.
Valor futuro: Representa un solo flujo de dinero que se entrega al final del
último período de inversión. Se puede calcular a partir de una suma presente,
una serie de cuotas uniformes o a partir de una serie de cuotas no uniformes.
También se puede trabajar con tasas de interés iguales para todos los periodos
o con tasas de interés diferentes en cada uno de estos.
95
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
7. Resumen de fórmulas
FACTORES DE CONVERSION
Pagos
uniformes
Períodos
iguales
Tasa
constante
Opciones para el calculo del Valor Futuro
N.A.
SI
SI
VA * (1 + i ) n
N.A.
SI
NO
VA * [(1 + i1 ) * (1 + i2 ) * ..... * (1 + in )]
Una cuota
uniforme
SI
SI
SI
PAGO * ⎢
Una cuota
NO uniforme
NO
SI
SI
Cálculo de
VF a partir
de:
Una suma
presente
Una suma
presente
Una cuota
NO uniforme
NO
SI
NO
Fórmula
Función en
Excel
VF
⎡ (1 + i ) n − 1⎤
⎥
i
⎣
⎦
PAGO1 * (1 + i )n −1 + PAGOt * (1 + i )n −t + ...
PAGO n −1 * (1 + i )1 + PAGO n
PAGO1 * [(1 + i 1 ) * (1 + i 2 ) * ..... * (1 + i n )] + ...
PAGO 2 * [(1 + i 2 ) * ..... * (1 + i n )] + ...
PAGO n −1 * [(1 + i n )] + ...
PAGO n
VF.PLAN
VF
No existe
No existe
Cálculo de
VP a partir
de:
Pagos
uniformes
Períodos
iguales
Tasa
constante
Opciones para el calculo del Valor Futuro
Una suma
futura
N.A.
SI
SI
VF
(1 + i ) n
Una suma
futura
N.A.
SI
NO
[(1 + i 1 ) * (1 + i 2 ) * ..... * (1 + i n )]
Cuotas
uniforme
SI
SI
SI
PAGO * ⎢
Fórmula
Función en
Excel
VA
VF
⎡ (1 + i ) n − 1⎤
n ⎥
⎣ i (1 + i ) ⎦
96
No existe
VA
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
Cálculo de
VP a partir
de:
Pagos
uniformes
Períodos
iguales
Tasa
constante
Opciones para el calculo del Valor Futuro
Cuotas NO
uniforme
NO
SI
SI
Cuota NO
uniforme
NO
SI
NO
Cuota NO
uniforme
NO
NO
SI
Función en
Excel
Fórmula
PAGO1 PAGOt
PAGO n −1 PAGO n
+
+ ... +
+
(1 + i )1 (1 + i ) 2
(1 + i )n −1 (1 + i )n
PAGO1
PAGO 2
+
+ ....
(1 + i 1 ) [(1 + i 1 ) * (1 + i 2 )]
PAGOn −1
+ ...
[(1 + i 1 ) * (1 + i 2 ) * ....(1 + i n −1 )]
PAGOn
[(1 + i 1 ) * (1 + i 2 ) * ....(1 + i n −1 ) + (1 + i n )]
VNA
No existe
VNA.NO.PER
N.A.: No aplica
TASAS EQUIVALENTES
Cálculo
de
A partir de Nominales
En excel: N.A.
Periódicas
i periodico
i
= no min al
n
Nominales N.A.
A partir de
Periódicas
A partir de Efectivas
En excel: N.A.
i periodico = n (1 + i ef . ) − 1
N.A.
i nom . = n *
i nom . = i per . * n
[ (1 + i
n
ef .
) − 1]
En Excel: Int. Efectivo
⎛
i ef . = ⎜1 +
Efectivas
⎝
n
i nom .venc . ⎞
⎟ − 1.
n ⎠
En Excel: N.A.
⎛
i ef . = ⎜1 −
⎝
i nom .ant . ⎞
⎟
n ⎠
En Excel: N.A.
n
i ef . = (1 + i per .ven . ) − 1
N.A.
En Excel: N.A.
−n
i ef . = (1 − i per .ven . ) − 1
−n
− 1.
Las siguientes fórmulas solo aplican para tasas periódicas:
i vencido =
i anticipado
1 − i anticipado
i anticipado =
97
i vencido
1 − i vencido
Matemáticas Financieras
PUJ
Copyright® Julio A. Sarmiento Sabogal y Edgardo Cayón Fallon
TABLAS DE AMORTIZACION
Cuota Fija:
Periodo
Saldo inicial
Intereses
Abono a
capital
0
No existe
No existe
No existe
1
Saldo final
del periodo
anterior
Saldo inicial
Cuota menos
por la tasa de
intereses
interés
Cuota
No existe
PAGO = VA
i (1 + i ) n
(1 + i ) n − 1
Saldo final
Valor del
crédito
Saldo inicial
menos abono
a capital
Abono a capital Uniforme:
Periodo
Saldo inicial
Intereses
Abono a
capital
No existe
Cuota
Valor del
crédito
0
No existe
No existe
1
Saldo final
del periodo
anterior
Saldo inicial ABONO = VA Intereses mas Saldo inicial
n abono a
por la tasa de
menos abono
interés
capital
a capital
98
No existe
Saldo final