Gráfico Exponencial, Polinominal y Cuadrático
Anuncio

Gráfico Exponencial, Polinominal y Cuadrático
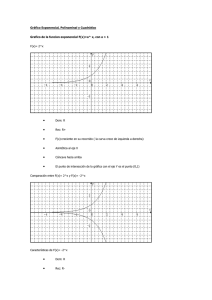
Grafico de la funcion exponencial F(x)=a^ x, con a > 1
F(x)= 2^x
• Dom: R
• Rec: R+
• F(x):creciente en su recorrido ( la curva crece de izquierda a derecha)
• Asintótica al eje X
• Cóncava hacia arriba
• El punto de intersección de la gráfica con el eje Y es el punto (0,1)
Comparación entre F(x)= 2^x y F(x)= −2^x
Características de F(x)= −2^x
1
• Dom: R
• Rec: R−
• F(x):decreciente en su recorrido ( la curva crece de derecha a izquierda)
• Asintótica al eje X
• Cóncava hacia abajo
• El punto de intersección de la gráfica con el eje Y es el punto (0,−1)
F(x) = 3^ x
• Dom: R
• Rec: R+
• F(x):creciente en su recorrido ( la curva crece de izquierda a derecha)
• Asintótica al eje X
• Cóncava hacia arriba
• El punto de intersección de la gráfica con el eje Y es el punto (0,1)
Comparacion entre F(x)= 2^x y F(x) = 3^x
2
Grafico de la función exponencial y= a^x, con 0 < a < 1
F(x)=( ½) ^x
• Dom: R
• Rec: R+
• F(x):creciente en su recorrido ( la curva crece de derecha a izquierda)
• Asintótica al eje X
• Cóncava hacia arriba
• El punto de intersección de la gráfica con el eje Y es el punto (0,1)
F(x) = (!) ^x
• Dom: R
• Rec: R+
• F(x):creciente en su recorrido ( la curva crece de derecha a izquierda)
• Asintótica al eje X
• Cóncava hacia arriba
3
• El punto de intersección de la gráfica con el eje Y es el punto (0,1)
Comparación entre F(x)=( ½) ^x y F(x) = (!) ^x
Grafico de la función F(x)= a^1, con a= 1
• Dom : R
• Rec : [ 1 ]
• F(x) constante
• Recta
• Asintótica al eje X
• El punto de intersección con el eje Y es el punto (0,1)
Conclusiones:
Si a > 1:
• La curva asociada a esta función exponencial intersecta al eje y en el punto (0,1)
4
• La función es creciente para todo valor de X
• Mientras a es mayor, mas se aproxima al eje Y
• La curva es asintótica al eje X (se acerca indefinidamente a el sin llegar a tocarlo)
Si a < 0 :
• La curva asociada a esta función intersecta al eje Y en el punto (0, −1)
• La función es decreciente para todo valor de X
• Al igual que en el caso anterior la curva es asíntota al eje X
• La curva se presenta como un reflejo de su inverso aditivo
Si 0 < a < 1:
• La curva asociada a esta función exponencial intersecta al eje Y en el punto (0,1)
• La función es decreciente para todo valor real de X
• Mientras a se acerca mas a 1, la curva se hace mas recta alejándose del eje Y.
• La curva es asintótica al eje X
Si a = 1
• Se observa que para todo valor real de x se tiene y= 1, de lo cual resulta una recta paralela al eje X, es
decir, se trata de una función constante.
Casos particulares de Funciones Exponenciales
Entre las funciones exponenciales merecen especial atención aquellas que tienen como base los números e y
10
F(x)= e ^ x
• Dom: R
• Rec: R+
• F(x):creciente en su recorrido ( la curva crece de izquierda a derecha)
• Asintótica al eje X
• Cóncava hacia arriba
5
• El punto de intersección de la gráfica con el eje Y es el punto (0,1)
F(x)= 10^ x
• Dom: R
• Rec: R+
• F(x):creciente en su recorrido ( la curva crece de izquierda a derecha)
• Asintótica al eje X
• Cóncava hacia arriba
• El punto de intersección de la gráfica con el eje Y es el punto (0,1)
Conclusiones:
Ambas curvas presentan las mismas características de una función exponencial con a > 1.
Gráficos de las Funciones Potenciales
F(x)= x ²
6
• Dom: R
• Rec: R+
• F(x) creciente en su recorrido (parábola)
• Cóncava hacia arriba
• Intersecta el eje X e Y en el punto (0,0)
• La funcion y = x ², es par pues se obtienen los mismos valores de e independiente del signo de x
F(x) = x ³
• Dom: R
• Rec: R
• F(x) creciente para toda medida angular a su dominio
• Intersecta el eje X e Y en el punto (0,0)
• La función y = x ³, impar, pues (−x) = − y, por lo tanto es simétrica respecto del origen
F(x)= x^4
7
• Dom: R
• Rec: R+
• F(x) creciente en su recorrido en los intervalos [ −½, "[, [ ½, "[
• Intersecta el eje X e Y en los puntos (0,0), (−½, 0), (½, 0)
• La funcion y = x ², es par pues se obtienen los mismos valores de e independiente del signo de x
F(x) = x ² + 1
• Dom: R
• Rec: R+ salvo el intervalo entre el 0 y el 1
• F(x) creciente en su recorrido (parábola)
• Cóncava hacia arriba
• Intersecta el eje Y en el punto (0,1)
• La funcion y = x ² + 1, es par pues se obtienen los mismos valores de e independiente del signo de
x
F(x)= x ² − 1
8
• Dom: R
• Rec: R+ [ 0,−1]
• F(x) creciente en su recorrido (parábola)
• Cóncava hacia arriba
• Intersecta el eje X en los puntos ( −1, 0) y (1,0) y al eje Y en el punto (0,−1)
• La funcion y = x ² − 1, es par pues se obtienen los mismos valores de e independiente del signo de
x
F(x) = x ² + 2x+1
• Dom: R
• Rec: R+
• F(x) creciente en su recorrido (parábola)
• Cóncava hacia arriba
• Intersecta el eje X en el punto ( −1, 0) y al eje Y en el punto (0,1)
• La funcion y = x ² − 1, es par pues se obtienen los mismos valores de e independiente del signo de x
Conclusiones
• Para toda función cuadrática el dominio serán R
• El recorrido puede variar dependiendo si el existe una suma o resta, de esta manera :
♦ Si sumamos 1 la curva se desplaza 1 lugar de hacia arriba de su posición original volviéndose
asintótica
♦ Si restamos 1 se desplaza 1 lugar hacia debajo de su posición original intersectando al eje X
en dos puntos
• En el caso de encontrarnos con una ecuación cuadrática la curva se corre un lugar hacia la
izquierda de su posición original (F(x) = x ² + 2x+1)
Grafico de la Función Logarítmica
Grafica de la función logarítmica y = b log x , con b> 1
F(x)= x log2
9
• Dom : R+
• Rec: R
• F(x) creciente en se dominio
• Asintótica al eje Y
• Cóncava hacia abajo
• El punto de intersección con el eje X es el punto (1, 0)
F(x)= x log 3
• Dom : R+
• Rec: R
• F(x) creciente en se dominio
• Asintótica al eje Y
• Cóncava hacia abajo
• El punto de intersección con el eje X es el punto (1, 0)
Grafica de la función logarítmica y = b log x , con 0 < b < 1
10
F(x)= x log !
• Dom : R+
• Rec: R
• F(x) creciente en se dominio
• Asintótica al eje Y
• Cóncava hacia arriba
• El punto de intersección con el eje X es el punto (1, 0)
F(x) = x log !
• Dom : R+
• Rec: R
• F(x) creciente en se dominio
• Asintótica al eje Y
• Cóncava hacia arriba
• El punto de intersección con el eje X es el punto (1, 0)
11
Conclusiones:
Si b > 1:
• La curva asociada a la funcion logarítmica intersecta al eje X en el punto (1,0)
• La función es creciente para todo valor de x
• La curva es asintótica al eje Y
Si 0 < b < 1
• La curva asociada a la funcion logarítmica intersecta al eje x en el punto (1,0)
• La función es decreciente para todo valor real de x
• La curva es asintótica al eje Y
En síntesis:
Las características de las funciones logarítmicas y = x log b, con b perteneciente a los reales positivos incluido
el −1, son:
• El dominio es el conjunto de los números reales positivos
• El recorrido es el conjunto de los números reales
• La curva asociada a la función logarítmica intersecta al eje X en el punto (1,0)
• Si b> 1, entonces la función es creciente
• Si 0<b<1, entonces la función es decreciente
Gráficos de Funciones trigonométricas.
F(x) = Sen
• Dom: R
• Rec : [ −1, 1]
• La función seno toma entre −1 y 1, por lo tanto esta definida por todos los Números Reales entre estos
dos números.
• El comportamiento de la curva esta representada en el siguiente cuadro
12
Cuadrante
I
II
III
IV
Comportamiento de y= sen x
Creciente positiva
Decreciente positiva
Creciente negativa
Decreciente negativa
Valores que toma y = sen x
0< sen x < 1
1> sen x > 0
0 > sen x > −1
−1< sen x < 0
• Es una función impar, pues (−x) = − sen x, ðð x "Dom (funcion seno), por lo tanto es simétrica
respecto del origen
• Es periódica de periodo t = 2 ð
• Es creciente en los intervalos como ] −2 ð, − 3ð / 2[ ; ] − ð / 2, ð / 2[ , ...
• Es decreciente en los intervalos como ] 3ð / 2 , ð / 2[; ] ð / 2 , 3 ð / 2 [, ...
• No es inyectiva: ð x ð x tal que sen x = sen x
• No es Sobreyectiva Rec( función seno) = [ −1, 1]
• Por lo tanto no es biyectiva y no tiene función inversa
• Alcanza un valor :
♦ Máximo y = 1
♦ Minimo y = −1
F(x) = cos
• Dom : R
• Rec : [ −1, 1]
• Es una función par, pues cos (x)= cos (− x), por lo tanto, es simétrica respecto del eje Y
• Es periódica, de periodo t = 2ð
• Es creciente en intervalos como ] ð, 0 [ , ] ð, 2ð [, ....
• Es decreciente en intervalos como ] −2 ,− ð [, ] 0, ð [, ....
• Es continua en R
• No es inyectiva : ð x ð x tal que cos x = cos x
• No es Sobreyectiva Rec( función coseno) = [ −1, 1]
• Por lo tanto no es biyectiva y no tiene función inversa
• Alcanza un valor :
♦ Máximo y = 1
♦ Minimo y = −1
13
− Su comportamiento se puede resumir en el siguiente cuadro:
Cuadrante
I
II
III
IV
Comportamiento de y= cos x
Decreciente positiva
Decreciente negativa
Creciente negativa
Creciente positiva
Valores que toma y = cos x
1> sen x > 0
0 > sen x > −1
−1< sen x < 0
0< sen x < 1
F(x) = Tan
• Dom : R − {ð / 2 ± k ð} ; k"N
• Rec: R
• Es una funcion impar, pues (−x) = − tan x, ðð x "Dom (funcion tangente), por lo tanto es simétrica
respecto del origen
• Es periódica, de periodo = ð
• Es creciente para toda medida angular a su dominio
• Es continua en Dominio( función tangente).
• No es inyectiva : ð x ð x tal que tan x = tan x
• No es Sobreyectiva Rec( función tangente) = [ −1, 1]
• Por lo tanto no es biyectiva y no tiene función inversa
• No es una función acotada, ya que puede tomar cualquier valor real
• Es cero o nula para medidas angulares múltiplos de ð, tales como:
♦ −2ð, −ð, 0, ð, 2ð,... es decir: tan (kð) = 0 ; ðð k " Z
F(x) = cosec x
14
F (x) = cot x
• Dom : R − {ð / 2 ± k ð} ; k"N
• Rec: R
• Es una funcion impar, pues (−x) = − tan x, ðð x "Dom (funcion tangente), por lo tanto es simétrica
respecto del origen
• Es periódica, de periodo = ð
• Es decreciente para toda medida angular a su dominio
• Es continua en Dominio( función tangente).
• No es inyectiva : ð x ð x tal que tan x = tan x
• No es Sobreyectiva Rec( función tangente) = [ −1, 1]
• Por lo tanto no es biyectiva y no tiene función inversa
• No es una función acotada, ya que puede tomar cualquier valor real
• Es cero o nula para medidas angulares múltiplos de ð, tales como:
♦ −2ð, −ð, 0, ð, 2ð,... es decir: tan (kð) = 0 ; ðð k " Z
F(x) = sec
15
F(x) = 2 sen x
• Dom: R
• Rec : [ −2, 2]
• La función seno toma entre −2 y 2, por lo tanto esta definida por todos los Números Reales entre estos
dos números.
• El comportamiento de la curva esta representada en el siguiente cuadro
Cuadrante
I
II
III
IV
Comportamiento de y= sen x
Creciente positiva
Decreciente positiva
Creciente negativa
Decreciente negativa
Valores que toma y = sen x
0< sen x < 2
2> sen x > 0
0 > sen x > −2
−2< sen x < 0
• Es una función impar, pues (−x) = − sen x, ðð x "Dom (funcion seno), por lo tanto es simétrica
respecto del origen
• Es periódica
16
• Es creciente en intervalos y decreciente por intervalos
• No es inyectiva: ð x ð x tal que sen x = sen x
• No es Sobreyectiva Rec( función seno) = [ −1, 1]
• Por lo tanto no es biyectiva y no tiene función inversa
• Alcanza un valor :
♦ Máximo y = 2
♦ Minimo y = −2
F(x) = 2 sen ( x+ ð)
F(x) = 2 sen (2x + ð)
Conclusiones
• El dominio de las funciones seno y coseno es todo R. Mientras tanto, en la definición de tangente y de
secante aparece la abscisa x en el denominador, por lo tanto deben excluirse de su dominio todos los
valores de q para los cuales x = 0; es decir hay que excluir los ángulos de medida, donde n es un
número entero. El dominio de la tangente y la secante es entonces:
17
R−
− Están excluidos, por ejemplo, valores tales como:
ð , −ð /2, 3ð /2, −3ð /2, 5ð /2, −5ð /2
(todos los "múltiplos impares" de
).
Por otro lado, en la definición de cotangente y cosecante aparece la ordenada y en el denominador. De manera
que el dominio de estas dos funciones excluye todos los valores de la forma p , con n entero. Quedan fuera,
por ejemplo, los números:
0, ð , −ð , 2ð , −2ð
(todos los "múltiplos de p ").
Sistemas:
x ² + y ² = 36
xy=6
Las ecuaciones de este sistema corresponden a una circunferencia y una hipérbola.
18