FUERZAS (PARTE I) INTRODUCCIÓN

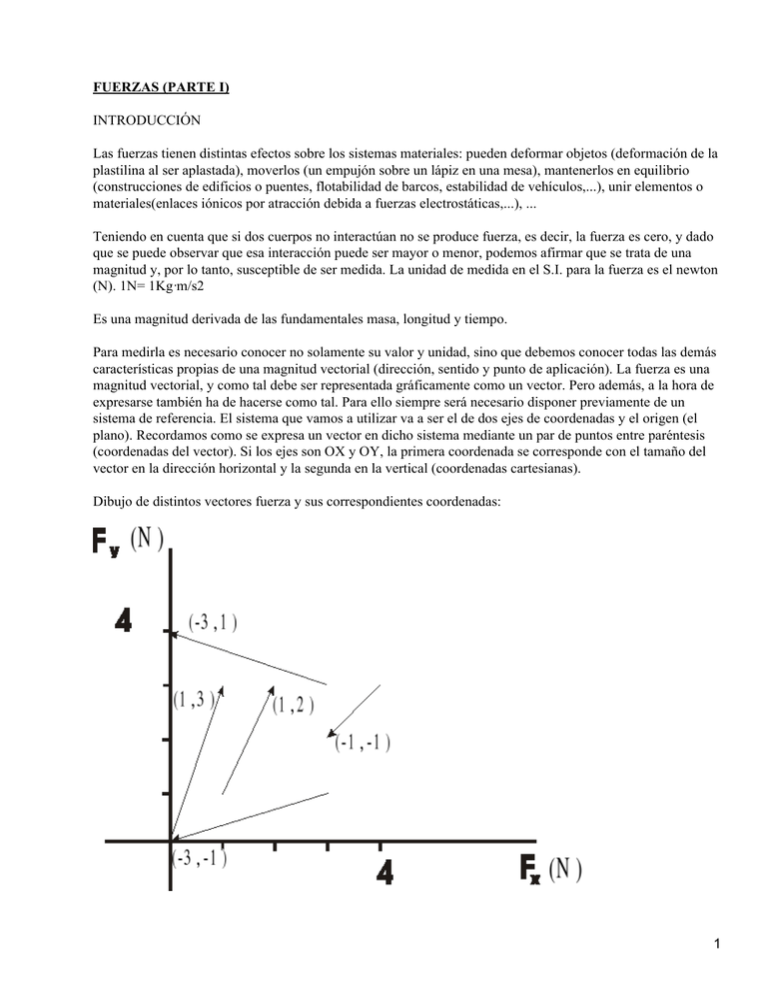
FUERZAS (PARTE I)
INTRODUCCIÓN
Las fuerzas tienen distintas efectos sobre los sistemas materiales: pueden deformar objetos (deformación de la
plastilina al ser aplastada), moverlos (un empujón sobre un lápiz en una mesa), mantenerlos en equilibrio
(construcciones de edificios o puentes, flotabilidad de barcos, estabilidad de vehículos,...), unir elementos o
materiales(enlaces iónicos por atracción debida a fuerzas electrostáticas,...), ...
Teniendo en cuenta que si dos cuerpos no interactúan no se produce fuerza, es decir, la fuerza es cero, y dado
que se puede observar que esa interacción puede ser mayor o menor, podemos afirmar que se trata de una
magnitud y, por lo tanto, susceptible de ser medida. La unidad de medida en el S.I. para la fuerza es el newton
(N). 1N= 1Kg·m/s2
Es una magnitud derivada de las fundamentales masa, longitud y tiempo.
Para medirla es necesario conocer no solamente su valor y unidad, sino que debemos conocer todas las demás
características propias de una magnitud vectorial (dirección, sentido y punto de aplicación). La fuerza es una
magnitud vectorial, y como tal debe ser representada gráficamente como un vector. Pero además, a la hora de
expresarse también ha de hacerse como tal. Para ello siempre será necesario disponer previamente de un
sistema de referencia. El sistema que vamos a utilizar va a ser el de dos ejes de coordenadas y el origen (el
plano). Recordamos como se expresa un vector en dicho sistema mediante un par de puntos entre paréntesis
(coordenadas del vector). Si los ejes son OX y OY, la primera coordenada se corresponde con el tamaño del
vector en la dirección horizontal y la segunda en la vertical (coordenadas cartesianas).
Dibujo de distintos vectores fuerza y sus correspondientes coordenadas:
1
Al igual que los vectores se suman, restan o son multiplicados por un número también los vectores fuerza
responden a dichas operaciones.
Dados =(−2 , 7) y = (3 , 5) − = (−2 , 7) − (3 , 5) = (−5 , 2)
+ = (−2 , 7) + (3 , 5) = (1 , 12)
3'2· = 3'2· (3 , 5) = (9'6 , 16)
Construcción gráfica de dichas operaciones:(en clase)
El módulo de un vector se calcula como la raíz cuadrada positiva de la suma de los cuadrados de sus
coordenadas cartesianas, y se corresponde con lo que mide:
Dado F(4N, 3N), su módulo
Dibujo del cálculo de dicho módulo:
LEY DE HOOKE
Cuando a los materiales se les somete a esfuerzos (aplicación de fuerzas) se pueden producir deformaciones
en los mismos. Dichas deformaciones pueden ser temporales (mientras dura la fuerza) o permanentes (si una
vez la fuerza deja de actuar el material no vuelve a su forma inicial. Todos los materiales tienen un límite de
esfuerzo a partir del cual ya no vuelven dicha forma, este límite se llama límite de elasticidad. Además de esto
cuando la fuerza se intensifica más el material puede llegar a romperse: punto de ruptura.
Algunos materiales cuando se ven sometidos a esfuerzo en los límites de elasticidad, la deformación es
proporcional a la fuerza aplicada, caracterizándose la correspondiente gráfica F−L o F−ðL por ser una recta
creciente. La constante que relaciona la fuerza con la elongación (alargamiento o estiramiento o ðL) es la
constante de elasticidad K. La relación entre ellas se llama Ley Hooke:
F = K·(L−L0) = K· ðL
siendo L la longitud del material sometido a fuerza F, L0 longitud del material en reposo (sin estar sometido a
esfuerzo) y K constante de elasticidad que depende del material.
F(N) ruptura
F(N)
L0 L(m) L0 L(m)
Gráfica que sigue la ley de Hooke Gráfica real completa de un material
Cuanto mayor sea K, mayor F habrá que realizar para deformar el material.
Planteamiento de problemas relacionados con la Ley de Hooke.
LEY DE LA GRAVITACIÓN UNIVERSAL
Enunciada por Isaac Newton en el siglo XVII: Dos masas cualesquiera m1 y m2, situadas entre sí a una
distancia d, se atraen con una fuerza, FN que es directamente proporcional al producto de las mismas e
2
inversamente proporcional al cuadrado de las distancias que las separa
con G constante Gravitatoria de valor 6'67·10−11 N·m2/kg2, d distancia en los cuerpos de masas m1 y m2.
Las fuerzas gravitatorias son responsables de las trayectorias y movimientos de los astros, así como del peso.
Éste es un tipo de fuerza a la que acostumbramos a confundir con la masa. El peso es la fuerza con la que la
Tierra atrae a los objetos que se encuentran en su superficie. Pero también dichos objetos atraen para sí a la
Tierra, claro que dada la masa de la misma apenas se inquieta.
El peso se calcula como P = m · g
g es la aceleración de la gravedad y su valor en el S.I. es 9'8 m/s2.
Este valor de g no es constante, sino que está calculado como el valor de la aceleración con que la Tierra atrae
a los objetos que hay sobre ella, esto es a 0 m de altitud sobre el nivel del mar. Por encima de dicho nivel este
valor disminuirá.
A nivel del mar la fuerza gravitatoria de interacción entre la Tierra de masa aproximada MT = 5'98·1024 kg y
un objeto de masa m (cualquiera) es igual que su peso:
puesto que la distancia d es el radio de la Tierra: 6370000 m
Planteamiento de problemas relacionados con las fuerzas gravitatorias (gravedad en la Luna u otros astros,
fuerzas o distancias entre cuerpos de diversas masas,...)
COMPOSICIÓN DE FUERZAS
Es la operación de determinar la fuerza resultante.
Composición de fuerzas de igual punto de aplicación:
− Igual dirección y sentido
− Igual dirección y distinto sentido
si ambas son iguales la resultante es nula
− Oblicuas:
Composición de fuerzas paralelas con distinto punto de aplicación:
Cuando se componen o suman dos fuerzas paralelas se debe producir el efecto de obtener una resultante que
produzca la misma traslación y giro que ambas.
• Fuerzas paralelas de igual sentido (figura inferior izquierda):
• El módulo de la resultante ha de ser la suma numérica de ambas fuerzas.
• Su dirección paralela a la de las componentes.
• Su sentido es el mismo de las fuerzas aplicadas.
3
• El punto de aplicación de la resultante ha de cumplir: F1 · x1 − F2 · x2 = 0, pues la distancia de la resultante
al punto de giro es cero y por tanto el momento es nulo. Este punto está en el segmento que une los puntos
de aplicación de las fuerzas.
x1 x2
lx
• Fuerzas paralelas de distinto sentido (figura anterior derecha):
• El módulo de la resultante ha de ser la diferencia numérica de ambas fuerzas.
• Su sentido es el de la fuerza mayor aplicada.
• El punto de aplicación de la resultante ha de cumplir: F1 · (x + l)d1 − F2 · x = 0, pues la distancia de la
resultante al punto de giro es cero y por tanto el momento es nulo. Este punto está fuera del segmento que
une los puntos de aplicación de las fuerzas.
DESCOMPOSICIÓN DE FUERZAS
Cualquier fuerza puede ser descompuesta en otras dos perpendiculares. El valor de la intensidad de una de
ellas puede calcularse sabiendo la intensidad de la resultante y el ángulo que forma con las perpendiculares.
Razones trigonométricas....
Realización de operaciones con vectores analítica y gráficamente.
PAR DE FUERZAS
Se denomina par de fuerzas a dos fuerzas paralelas, iguales en módulo y de sentidos contrarios.
La resultante del par de fuerzas es 0.
El par de fuerzas no produce movimiento alguno de translación pero sí un giro.
El efecto del giro producido por el par de fuerzas se mide con su momento del par, cuyo módulo es
M = F · d, siendo d la distancia que hay entre ambas fuerzas y denominándose brazo del par.
MOMENTO DE UNA FUERZA
Es una magnitud que mide el efecto del giro producido por una fuerza. Se calcula numéricamente:
M = F · d , que es el valor en módulo. Experimental y por definición.
Es + si es antihorario. Y − si es un giro horario. Regla del tornillo o de Maxwell.
Unidades de N·m.
Veremos posteriormente s ESTÁTICA
La estática es precisamente la parte de la Física que estudia el equilibrio de los sólidos−rígidos, entendiendo
como tales a aquellos cuerpos que no se deforman al aplicarles una fuerza.
4
El c.d.g.
El c.d.g. de un sólido rígido es el punto de aplicación de la fuerza de atracción de la Tierra sobre el mismo,
siendo esa fuerza la resultante de todas las fuerzas de atracción que actúan sobre cada partícula por la que está
compuesto dicho sólido.
Determinación de c.d.g. en figuras planas....
Constatación de que dicho centro puede estar fuera del propio cuerpo.
Notación del sumatorio: .
Condiciones de equilibrio.
Se produce cuando la resultante de las fuerzas es cero y la suma de los momentos que actúan sobre él (los + y
−) es cero.
• Si el cuerpo esta inicialmente en reposo y al aplicar las fuerzas:
• La resultante es nula, entonces no se desplazará.
• La suma de sus momentos es nula, entonces no girará:
• Si el cuerpo esta inicialmente en movimiento y se cumplen las condiciones de equilibrio, entonces se
mantendrá el movimiento que posea.
Por lo tanto, la condición de equilibrio no implica necesariamente reposo
Aunque el punto respecto al cual se calcula la resultante es indiferente, se suele tomar aquel que más
convenga, y como habitualmente decimos que el cuerpo se traslada o gira respecto a su c.d.g. éste será el que
elegimos.
Ejercicios y problemas de balancines y fuerza resultante en ángulos oblicuos.
Sólidos y equilibrio.
Un sólido se puede encontrar en equilibrio cuando esta apoyado sobre una superficie o cuando está colgado de
un punto.
Este equilibrio puede ser: estable, inestable o indiferente.
En un sólido suspendido de un punto hay equilibrio cuando el c.d.g. y el punto están en la vertical.
♦ Cuando el c.d.g. está por debajo del punto de suspensión el equilibrio es estable.
♦ Cuando el c.d.g. está por encima del punto de suspensión es inestable.
♦ Cuando coinciden el c.d.g. y el punto de suspensión el equilibrio es indiferente.
Si el sólido no tiene el punto de suspensión y el c.d.g. en la vertical NO hay equilibrio.
En un sólido apoyado cuando la vertical que pasa por el c.d.g. cae dentro de la base de sustentación hay
equilibrio. Puede que este sea estable, inestable o indiferente. Dibujos de los casos (clase)
Si la vertical sobre el c.d.g. no cae sobre la superficie de apoyo NO hay equilibrio. Dibujo:
5
Conclusiones acerca del momento nulo:
♦ Un sólido−rígido permanecerá en equilibrio siempre que la vertical que traza el peso aplicado
sobre su c.d.g. pase por la base sobre la que se apoya, porque el momento que crea dicho peso
es cero.
♦ Si se desplaza mínimamente de esta posición de equilibrio estable manteniendo la vertical
sobre su base de apoyo, recuperará su equilibrio al dejar de actuar sobre él.
Explicación de ejemplos: coches de carrera, barcos de carga.
Cuanto más bajo se encuentre el c.d.g. de un sólido−rígido mayor estabilidad tendrá.
DINÁMICA
Leyes de Newton de la dinámica.
Primera Ley: Principio de inercia.
Todo cuerpo permanece en sus estado de reposo o movimiento a no ser que fuerzas ajenas actúen sobre él.
Segunda Ley: Principio fundamental de la Dinámica.
Cuando a un cuerpo se le somete a distintas fuerzas, se producen en él distintas aceleraciones. El cociente
entre dichas fuerzas y sus correspondientes aceleraciones es constante. Esta constante se llama masa inercial o
simplemente masa (explicación de inercial).
De ella se deduce la expresión general que constituye la
ECUACIÓN FUNDAMENTAL DE LA DINÁMICA:
Siendo m la masa del sistema y a la aceleración del sistema.
Tercera Ley: Ppio. De acción y reacción.
Cuando un cuerpo se ve sometido a la fuerza de acción, este reacciona a su vez con otra fuerza de reacción
que es igual en módulo y dirección y de sentido contrario a la de acción.
Fuerza Normal.
Es una fuerza perpendicular a la superficie de contacto con el cuerpo. Se trata de la fuerza de reacción de la
superficie (esta fuerza puede sostener total o parcialmente al cuerpo que se apoya en la superficie). Se la suele
expresar como N. Ejemplos.
Fuerzas de rozamiento.
Son fuerzas de oposición al movimiento de los cuerpos. Por lo tanto no existen si tampoco existen fuerzas que
tiendan a mover el cuerpo. De hecho ni existirían si no se llega a producir movimiento. Por todo ello queda
claro que llevan la misma dirección del movimiento pero sentido contrario. Se expresan como FR, y su valor
es: FR = · N. El símbolo es el coeficiente de rozamiento. Se definen dos tipos de fuerzas de rozamiento:
estática y dinámica. La estática es la fuerza necesaria para vencer una situación inicial de parada y la dinámica
es la del rozamiento que se produce cuando hay movimiento. Se define paralelamente a cada una de ellas los
correspondientes coeficientes de rozamiento estático y dinámico. En este curso sólo nos centraremos en el
6
rozamiento dinámico.
Ejemplos de cuerpos sobre planos horizontales, inclinados, combinación de ambos,... y muchos problemas...
La cantidad de movimiento.
.
Carácter vectorial. Unidades de kg·m/s
Principio de conservación de la cantidad de movimiento.
En un sistema aislado se conserva la cantidad de movimiento.
Ejemplos de choques elásticos: bolas de billar, coches, bala sobre objetos de mayor masa,...
u aplicación.
7
Fuerzas (I)
7