La Computadora en la Enseñanza de las Matemáticas Practica 5
Anuncio
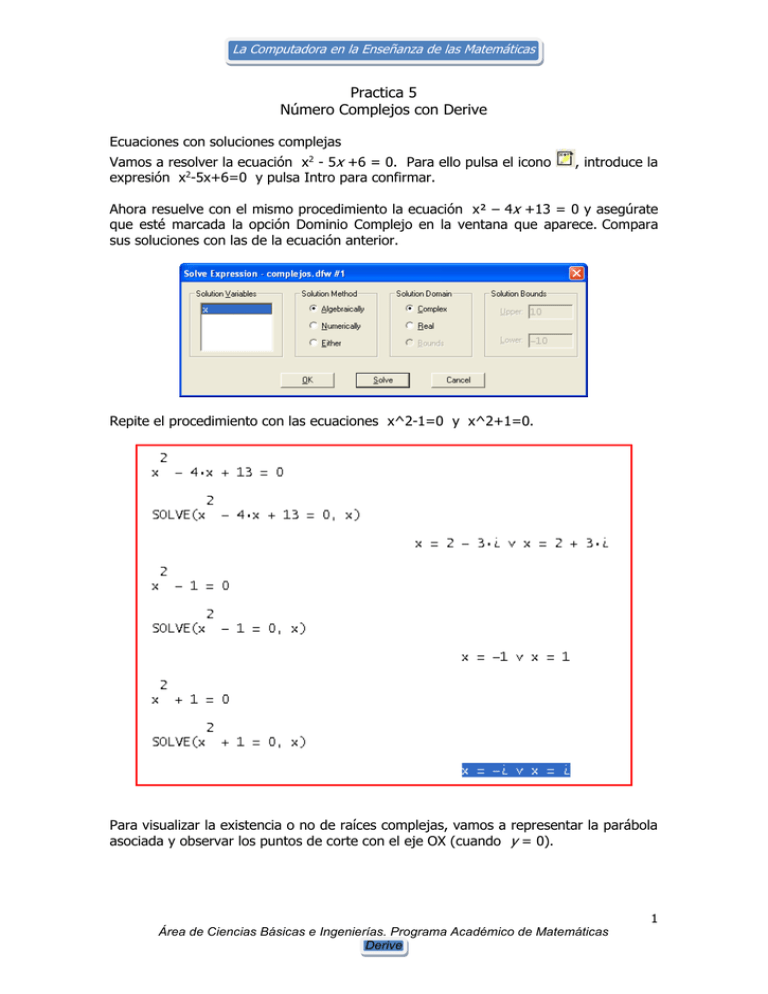
La Computadora en la Enseñanza de las Matemáticas Practica 5 Número Complejos con Derive Ecuaciones con soluciones complejas Vamos a resolver la ecuación x2 - 5x +6 = 0. Para ello pulsa el icono expresión x2-5x+6=0 y pulsa Intro para confirmar. , introduce la Ahora resuelve con el mismo procedimiento la ecuación x² – 4x +13 = 0 y asegúrate que esté marcada la opción Dominio Complejo en la ventana que aparece. Compara sus soluciones con las de la ecuación anterior. Repite el procedimiento con las ecuaciones x^2-1=0 y x^2+1=0. Para visualizar la existencia o no de raíces complejas, vamos a representar la parábola asociada y observar los puntos de corte con el eje OX (cuando y = 0). 1 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas Vamos a representar la función y=x^2-5x+6 para observar sus raíces. Para ello, introduce la expresión x^2-5x+6 y resáltala colocando el cursor sobre ella. A continuación, pulsa el icono para abrir la ventana de gráficos 2D. Una vez abierta es necesario volver a pulsar el mismo icono (pero en la ventana 2Dplot) para que se dibuje realmente la gráfica. Cada vez que se pulse el icono se redibuja la función activa en un nuevo color. En la parte inferior izquierda aparecen las coordenadas de la posición del cursor. Sitúa el cursor (aproximadamente) sobre los puntos en que la gráfica corta al eje OX y anota el valor de la abscisa que aparece abajo. Compara las raíces con las abscisas obtenidas. 1. Representa las funciones y=x^2+1, y=x^2-4x+13. Observa que la gráfica no corta al eje OX. 2. Resuelve e interpreta gráficamente las ecuaciones: x^2+6x+10=0 3x^2+27=0 3x^2-27=0 3. Resuelve e interpreta gráficamente las ecuaciones siguientes: x^2+x+1=0 2.3x^2+3.2x+17.5=0 (x-2)(x^2+4)=0 x^4+7=0 x^4+x^2+1=0 x^6+1=0 2 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas 4. Introduce la ecuación ax^2+bx+c=0 y resuélvela con DERIVE especificando la variable x. Observa que no puede haber soluciones reales cuando el radicando que aparece es negativo. Para detectar si una ecuación como la anterior tiene o no soluciones reales según los valores de a, b y c, introduce la siguiente definición en DERIVE: SOL(a,b,c):=IF( b^2-4ac<0,”Soluciones complejas”,”Soluciones reales”) Observa que usamos := en vez de = porque se trata de una definición, no de una ecuación. Para saber si x^2-4x+5= 0 tiene soluciones reales introduce y simplifica la expresión SOL(1,-4,5). Prueba con otras ecuaciones. La ecuación (x – 1)(x – 3)(x + 4) = 0 tiene como soluciones x = 1, x = 3 y x = – 4. Introduce la expresión (x - 1)(x - 3)(x + 4) = 0 y pulsa Intro. A continuación, pulsa CTRL+E y se abrirá una ventana. Confirma con el botón "Expandir" Vamos a buscar una ecuación que tenga por soluciones x = 2- i, x = 2+i: Para ello, introduce y simplifica la expresión (x-(2-î))(x-(2+î)). Para introducir î puedes hacer click sobre su símbolo en la lista superior de la ventana de introducción de expresiones, o pulsar CTRL+i, o usar el acento ^ . En DERIVE hay que distinguir la unidad imaginaria î de la variable i. 3 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas 5. Halla una ecuación que tenga por soluciones x = 2, x = i, x = –i. Halla una ecuación que tenga por soluciones x = 3, x = i. 6. Comprueba con ejemplos que si una ecuación tiene coeficientes reales, las soluciones complejas siempre van por parejas (una solución y su conjugado). Operaciones con números complejos 7. Introduce la expresión 3(2+î)-5(4-3î)+(7-2î) y simplifica. Comprueba el resultado. Repite el procedimiento con (2-5î)(7+3î). Repite el procedimiento con (4-7î)/(3+4î). Tras introducir la expresión, pulsa simplificar y, a continuación para , para aproximar. Señala la parte real y la imaginaria. 8. Define los números u:=2-3î, v:=1-î, w:=-3+2î (usa :=). Introduce y “simplifica” las siguientes expresiones: 3u+5v-4w 3uv+5uw-2 uw uv+uw u(v+w) u^2 uvw u^3 vuw u^(1/2) 4 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas CONVERSION DE FORMA BINÓMICA A POLAR Y DE POLAR A BINÓMICA DERIVE incorpora las siguientes funciones sobre números complejos en forma binómica que puedes utilizar: RE(u): Parte real de u. IM(u): Parte imaginaria de u. ABS(u): Módulo de u. PHASE(u): Argumento de u (en radianes). CONJ(u): Conjugado de u. Utilízalas con los complejos u, v, w definidos anteriormente. Define tu propia función-módulo de un complejo a + bi de la siguiente forma: MODULO(a,b):=(a^2+b^2) Comprueba que coincide con la función ABS, aplicándola a u, v y w. 9. Pasa a forma polar los siguientes números: 3-4î 4+3î 3+î î 5 -î -5 2.3+3.7î 5 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas 10 Define la siguiente función para pasar de forma polar bi: POLBIN(r,g):=r (cos g + î sin g) rg a forma binómica a + Para aplicarla a 5pi/4 introduce y simplifica la expresión POLBIN(5 , pi/4). Puedes introducir p como pi. Para aplicarla a 430º introduce y simplifica la expresión POLBIN(4 , 30º ) (el símbolo º se incluye para especificar que son grados, y no radianes. Puedes encontrarlo en la Barra de símbolos o sustituirlo por deg). Define una función para obtener la potencia n de un número complejo dado en forma polar rg: POT(r,g,n):=[r^n , ng] (Usa corchetes para incluir módulo y argumento). DERIVE proporciona la función MOD(n,m) que devuelve el resto de dividir m entre n. Podemos usarla para modificar la función anterior de esta forma: POTG(r,g,n):= [ r^n , MOD(ng,360)] o bien POTR(r,g,n):= [ r^n , MOD(ng,2pi)] si g va en radianes. Del mismo modo, define la función-producto en forma polar: PRODG( r,g,s,h):=[r s , MOD(g+h,360)] o bien PRODR( r,g,s,h):=[r s , MOD(g+h,2pi)] Utilízalas para hallar u2 y u v con u= 532º y v= 246º 6 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas Construye una función análoga para el cociente de números complejos en forma polar. Considera la siguiente función para hallar las raíces enésimas de un número complejo en forma polar rg: RAIZ(r,g,n):=[ r^(1/n) , g/n ] Esta función proporciona una sola raíz. Para obtener las n raíces introduce la siguiente función: RAIZG(r,g,n):= VECTOR ( [ r^(1/n) , (g+360k)/n ] , k, 0, n-1 ) (Con g en grados) RAIZR(r,g,n):= VECTOR ( [ r^(1/n) , (g+2kpi)/n ] , k, 0, n-1 ) (Con g en radianes) 11. Pruébala para hallar las tres raíces cúbicas de 860º. Para ello introduce y simplifica la expresión RAIZG(8,60,3). 7 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas Interpretación gráfica de las operaciones con números complejos Para representar el número complejo 3 + 4i introduce la expresión entre corchetes, [3,4], y pulsa el icono para abrir la ventana de gráficos. A continuación pulsa de nuevo el mismo icono en dicha ventana. Verás que se representa el punto. 12. Define el número (afijo) z:=[4,-3]. Escribe, simplifica y representa sucesivamente z, -z, [4,3]. Analízalo. Elimina los puntos dibujados. Introduce entre corchetes, simplifica y representa conjuntamente la expresión [z, [4,3],-z, [-4,-3]]. En la ventana de gráficos abre el menú Opciones-Pantalla, elige Puntos y marca Unir Sí. Vuelve a pulsar afijos representados? Elimina las gráficas. para representar. ¿Qué figura forman los 8 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas Define la siguiente función: AFB(z):=[RE(z),IM(z)] Esta función nos permite obtener las coordenadas del afijo de un número complejo en forma binómica. Define la función análoga para el caso de forma polar: AFP(r,g):=[r cos g , r sin g] 13. Define el número z:=3-4î. Representa (con los puntos conectados) la siguiente expresión: [ AFB(z) , AFB(CONJ(z)) , AFB(-z), AFB(CONJ(-z)) ] 14. Representa la siguiente expresión: [ AFP(1,0),AFP(1,72º),AFP(1,144º),AFP(1,216º),AFP(1,288º)] 9 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas Se trata de raíces quintas de la unidad. Elimina las gráficas anteriores. Introduce y simplifica la expresión RAIZG(1,0,5). Obtendrás una lista con las cinco raíces quintas de la unidad en forma polar. Abre la ventana de representaciones gráficas. Abre el menú Seleccionar y elige Sistema de coordenadas (o pulsa CTRL+Y) y marca la opción Polares Representa la lista de las cinco raíces (que permanecerá resaltada). 10 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas 15. Calcula y representa las 8 raíces octavas de la unidad. 16. Calcula y representa las raíces sextas de 6424º. 17. Comprueba que multiplicar z por 130º equivale a realizar un giro de 30º. Toma z = 345º. Halla el producto y representa los afijos correspondientes. Fórmula de Moivre Introduce la expresión (a+b)^3. Mientras permanece resaltada elige en el menú Simplificar la opción Expandir y marca las dos variables ( a y b). Confirma con el botón Expandir. Obtendrás el desarrollo de la potencia del binomio. Repite el proceso con (cos x+ î sin x)^3. En este caso no obtenemos el desarrollo buscado porque DERIVE simplifica el resultado como potencia compleja del número ê. Sin embargo, vamos a definir a y b convenientemente, y sustituir sus valores en la expresión de (a+b)^3. Introduce y simplifica [a:= cos x , b:= î sin x ]. Acabas de asignar un valor a a y b. Coloca el cursor sobre el desarrollo que obtuviste de (a+b)^3 y pulsa el icono de simplificar. La expresión se adaptará a los nuevos valores. Vamos a hallar la parte real de la última expresión sin tener que reescribirla. Para ello coloca el cursor sobre la expresión. Pulsa el icono de Introducción de expresiones y una vez abierta la ventana correspondiente escribe RE( y pulsa F3. La expresión resaltada se copiará automáticamente. Cierra el paréntesis y simplifica. El resultado obtenido es una fórmula para cos 3x. Si introduces y simplificas RE((cos x+ î sin x)^3) obtendrías simplemente cos 3x. Para la parte imaginaria debes escribir IM(, copiar el desarrollo como en el caso anterior y simplificar. El resultado será una fórmula para sen 3x. 11 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive La Computadora en la Enseñanza de las Matemáticas Para obtener fórmulas análogas para cos 5x y sen 5x procederíamos de forma similar. Pero al desarrollar (a+b)^5, se simplificaría con los valores asignados a a y a b. Por ello debes utilizar otras letras como (m+n)^5, o bien eliminar los valores anteriores con la expresión [ a:= , b:= ]. Completa el proceso. Halla una fórmula para sen 4x, cos 4x, sen 7x, cos 7x. 18. Comprueba la fórmula de sen 2x y cos 2x. Observa que 2 cos²x – 1 = cos²x – sen² x. 12 Área de Ciencias Básicas e Ingenierías. Programa Académico de Matemáticas Derive
