Curvas en perspectiva

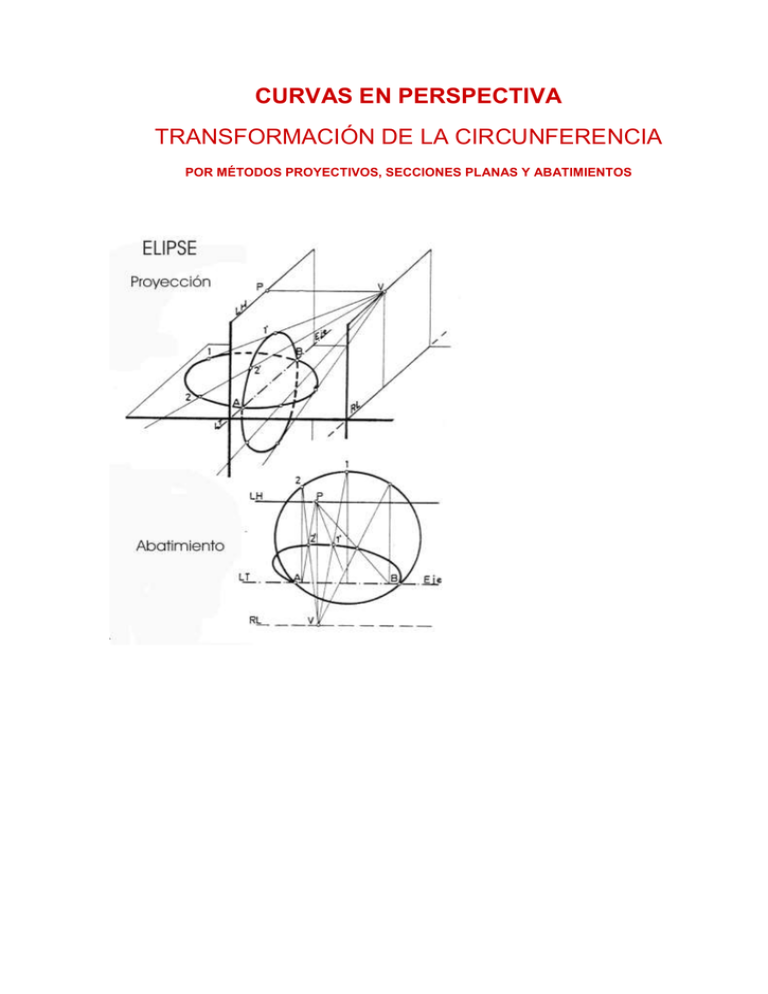
CURVAS EN PERSPECTIVA
TRANSFORMACIÓN DE LA CIRCUNFERENCIA
POR MÉTODOS PROYECTIVOS, SECCIONES PLANAS Y ABATIMIENTOS
Los métodos de la geometría plana sirven para el conocimiento de las propiedades de las curvas, pero
su trazado en perspectiva cónica, cuando deben hacerse por métodos directos, requieren otros trazados
más prácticos. Casi todas las curva en perspectiva se trazan a pulso, apoyándose en puntos métricos
hallados con auxilio de regla y compás. Las deformaciones de las curvas en perspectiva, son casos
particulares, pues dependen más que de su propia generación, del lugar y posición en que se
encuentren situadas respecto al punto principal de proyección.
MÉTODOS DE TRAZADOS GEOMÉTRICOS
Como método general se inscribe la figura curva en un cuadrilátero rectangular, que subdividido en
cuantos cuadriláteros sea conveniente, se forma una retícula o pauta de referencia, para trasladar,
punto a punto la figura curva a la perspectiva del rectángulo.
Circunferencia
Algunas curvas, por su estructura regular, como la circunferencia, tienen un trazado revisto por sus
conocidas propiedades. El cuadrado con sus diagonales, mediatrices y centros de arcos capaces,
facilitan el trazado directo de la circunferencia inscrita en la perspectiva del cuadrado.
Las propiedades que tiene la circunferencia respecto el cuadrado en geometría plana, las mantiene en
la perspectiva del cuadrado. En el caso primero de la figura 604, se comprueba que la circunferencia
pasa por los puntos medios de los lados del cuadrado, más por punto de las diagonales que se
encuentran a 1/7 del lado. En el segundo caso se verifica que el cuadrado puede contener, además de
los puntos medios de los lados, cuatro pares más por la construcción de arcos capaces. En la figura 605
son coordenadas paralelas a los lados las que determinan puntos de la circunferencia. En todo caso, la
circunferencia en perspectiva es una elipse, que conviene trazar a pulso, pues determinar sus ejes y
diámetros conjugados supone muchas operaciones poco prácticas.
SUPERFICIES REGLADAS DE REVOLUCIÓN
Cilindros
Trazadas las circunferencias directrices por los procedimientos que anteceden, la teoría pide la
determinación del punto de tangencia entre la curva y la recta, contorno aparente, que hace de
generatriz. Ese trazado es laborioso, por ello el métodos común es el trazado directo del enlace, curva
recta, por aproximación.
Conos
SUPERFICIES REGLADAS ALABEADAS
Hiperboloides y conoides
Los contornos aparentes de las alabeadas regladas, como los hiperboloides hiperbólicos de una hoja,
los conoides, los paraboloides hiperbólicos y los helicoides, se trazan con las rectas generatrices
consecutivas, y la evolvente que produce la curva tangente a esas rectas.
Aplicación de superficies de revolución
Aplicación de superficies regladas alabeadas