área ibérica

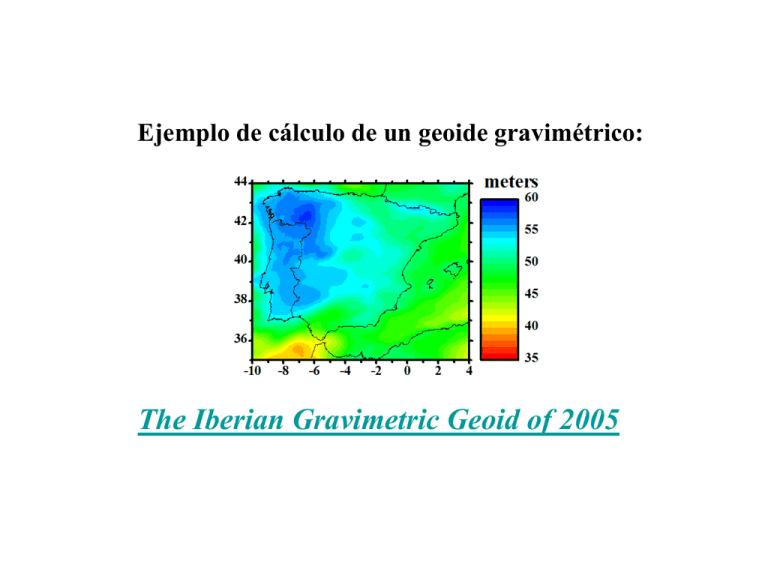
Ejemplo de cálculo de un geoide gravimétrico:
The Iberian Gravimetric Geoid of 2005
Figura de la Tierra en 1ª aproximación:
el elipsoide de revolución
normal
Relación entre altura ortométrica (H) y elipsoidal (h):
la ondulación del geoide (N)
H=h-N
Figura de la Tierra en 2ª aproximación: el geoide
cuya ondulación (N) se mide sobre el elipsoide
La nivelación con GPS o el cálculo de diferencias de
altura requiere el uso de un geoide para calcular DN
A
B
C
NB
Superficie
terrestre
H
NA h
HA = hA - NA
HB = hB - NB
DNBA = NB – NA  0
Geoide
Elipsoide
DHBA = DhBA - DNBA
DHBA  DhBA
Calculando DN para dos trayectos de 100 km,
podemos observar la diferencia que hay entre Dh y
DH, según sea la topografía
DN calculado en zona llana: trayecto AB
DN calculado en zona montañosa: trayecto CD
• En consecuencia, se requiere un modelo de geoide
para poder usar las medidas de altura GPS (h).
• Los modelos de geoide disponibles no poseen
precisión suficiente como para ser usados en la
mayor parte de los problemas de ingeniería.
• Es necesario el cálculo de un geoide para el área
ibérica, que tenga la mayor precisión posible.
Problema: cálculo de un geoide ibérico
DATOS NECESARIOS
• Datos de gravedad que pueden aportar diversos
organismos internacionales.
• Modelos digitales del terreno (DTM) que pueden
combinarse para obtener un DTM ibérico.
• Datos de validación del modelo que pueden
aportar organismos europeos.
Land and Marine Gravity Data
http://www.ngdc.noaa.gov/seg/
Land and Marine Gravity Data
http://bgi.cnes.fr:8110/bgi_debut_a.html
Land and Marine Gravity Data
http://www.usgs.gov/
A través de los organismos anteriores conseguimos
los datos de gravedad necesarios para el cálculo
http://www2.jpl.nasa.gov/srtm/
http://www.ngdc.noaa.gov/mgg/gdas/gd_designagrid.html
A través de los organismos anteriores conseguimos
los datos de elevaciones necesarios para el cálculo
Eliminamos los efectos de onda corta y de onda larga de
los datos de gravedad mediante:
Así conseguimos facilitar la interpolación de los puntos
aleatorios a una rejilla de puntos equidistantes (Corchete
et al., 2005)
El término href corresponde a las elevaciones filtradas
con un filtro de onda larga de 60 minutos de arco
El término DgGM se calcula mediante un modelo geopotencial
Dg GM 
GM
r
2
n máx

n 2
n
a
  (n - 1)
r
n
 Pnm (cos )Jnm cos m  K nm sen m
m 0
EIGEN-CG01C Gravity Anomalies (nmax = 360)
Los efectos de onda corta deben ser restaurados tras la
interpolación mediante:
Obtenida por interpolación
Para ello usaremos el modelo digital del terreno que
hemos calculado previamente (Corchete et al., 2005)
Obtenida por interpolación
Determinación de un geoide regional o local (N)
N = NGM + Nb + NI
NGM : contribución del modelo geopotencial
Nb : contribución de la gravedad residual
NI : efecto indirecto
NGM : contribución del modelo geopotencial
GM
N GM 
r
n máx

n 2
a
 
r
n n
 Pnm (cos )Jnm cos m  K nm sen m
m 0
http://www.gfz-potsdam.de/pb1/op/grace/results/index_RESULTS.html
EIGEN-CG01C Geoid (nmax = 360)
Nb : contribución de la gravedad residual
R
Nb 
4

Dg(, ) S()d

donde:
Dg = Dgfree + c + g ,, g = 0.3086 NI
c: corrección del terreno
(considerando sólo la masa sobre el geoide)
z
d
h
r
c  K
P
(z - h p )dz
h
[h
A
p


3
2
2
2 2
( x p - x )  ( y p - y)  ( h p - z )
]dxdy
z
rp
hp
x,y (geoide)
c
siendo f(x,y) y g:
f ( x , y) 
1
2
2 3/ 2
(x  y )

K 2
h  f - 2 h (f  h )  h 2 g
2
g
 f (x, y)dxdy
A

Nb : contribución de la gravedad residual
(obtenida integrando mediante la 1D FFT)
 n


RDD -1
N(, ) 
F1 
F1 (Dg cos) F1 (S) 
4G
   

1



donde:
F1-1 = FFT 1D inversa
F1 = FFT 1D directa

1
S(s) = - 4 - 6 s + 10s 2 - (3 - 6s 2 )ln s + s 2
s
sin 2

1
1
1
 PQ  sin 2 ( - )  sin 2 ( - ) cos  cos 
2
2
2
1
, , s  sin  PQ
2
NI : efecto indirecto
K 2
K
NI  h (x p , yp ) 
6
h 3 ( x , y) - h 3 ( x p , y p )
 (x p - x)2  (yp - y)2 3 / 2 dxdy
A
K 2 K
3 K 3
NI  h f h 
gh

6
6
siendo f(x,y) y g :
f ( x , y) 
1
2
2 3/ 2
(x  y )
g
 f (x, y)dxdy
A
VALIDACIÓN DEL MODELO
• La validación del modelo se realiza comparando
sus valores con datos de gran precisión.
• Estos datos son las ondulaciones del geoide (N0)
obtenidas mediante GPS/nivelación.
• Los datos de validación del modelo pueden ser
aportados por organismos europeos.
Proceso GPS/nivelación:
ondulaciones del geoide observadas
GPS satellite receiver
Leveling instrument
N0 = hGPS - Hlev
Organismos que pueden aportar datos de validación
European Vertical Reference System
(EVRS)
http://crs.bkg.bund.de/evrs/
Datos de la red vertical europea (EVRS) en Iberia
http://crs.bkg.bund.de/evrs/tabelle_neu.html
COMPARACIÓN CON OTROS MODELOS
• El geoide oficial usado en España (Sevilla, 1997):
the IBERian GEOid of 1995 (IBERGEO95).
• El geoide europeo (Denker and Torge, 1998): the
European Gravimetric Geoid 1997 (EGG97).
• Los geoides mundiales EGM96 y EIGEN-CG01C.
IBERian GEOid 1995 (IBERGEO95)
European Gravimetric Geoid 1997 (EGG97)
Modelos mundiales de geoide
http://cddis.gsfc.nasa.gov/926/egm96/egm96.html
EIGEN-CG01C Geoid
EGM96 geoid
CONCLUSIONES
• El geoide IGG2005 mejora todos los modelos de
geoide anteriores, siendo mucho más preciso.
• El geoide IGG2005 es un primer paso hacia un geoide
de precisión centimétrica.
• Para conseguir una precisión centimétrica
requieren más y mejores datos de gravedad.
se
REFERENCIAS
Corchete V., Chourak M. and Khattach D., 2005. The high-resolution
gravimetric geoid of Iberia: IGG2005. Geophys. J. Int., 162, 676–684.
Denker, H., and W. Torge. The European Gravimetric Quasigeoid
EGG97. International Association of Geodesy Syposia, Vol. 119,
Geodesy on the Move. Springer-Verlag, Berlin-Heidelberg-New York,
S. 249-254, 1998.
Sevilla, M. J. A new gravimetric geoid in the Iberian Peninsula. BGI
Bull. D’Inf. Nº 77 (Toulouse) and IGeS Bull. Nº 4 (Milano), 163-180,
1995.
CONTACTO
Prof. Dr. Víctor Corchete
Departamento de Física Aplicada
Escuela Politécnica Superior - CITE II(A)
UNIVERSIDAD DE ALMERIA
04120-ALMERIA
FAX: + 34 950 015477
e-mail: [email protected]
http://airy.ual.es/