Nombre y Apellidos: ___________________________________________________________ 4ºESO

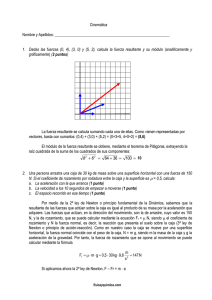
4ºESO
Dinámica
Nombre y Apellidos: ___________________________________________________________
1. Una persona arrastra una caja de 25 kg de masa sobre una superficie horizontal con una fuerza de 130 N. Si
el coeficiente de rozamiento por rodadura entre la caja y la superficie es  = 0,5, calcula:
a. La aceleración con la que arranca (1 punto)
b. La velocidad a los 10 segundos de empezar a moverse (1 punto)
c. El espacio recorrido en ese tiempo (1 punto)
d. Dibuja la gráfica v – t (1 punto) y s – t (2 puntos)
Por medio de la 2ª ley de Newton o principio fundamental de la Dinámica, sabemos que la resultante
de las fuerzas que actúan sobre la caja es igual al producto de su masa por la aceleración que adquiere. Las
fuerzas que actúan, en la dirección del movimiento, son la de arrastre, cuyo valor es 130 N, y la de
rozamiento, que se puede calcular mediante la ecuación Fr =  N, siendo  el coeficiente de rozamiento y N
la fuerza normal, es decir, la reacción que presenta el suelo sobre la caja (3ª ley de Newton o principio de
acción-reacción). Como en nuestro caso la caja se mueve por una superficie horizontal, la fuerza normal
coincide con el peso de la caja, N = m g, siendo m la masa de la caja y g la aceleración de la gravedad. Por
tanto, la fuerza de rozamiento que se opone al movimiento se puede calcular mediante la fórmula
Fr    m  g  0,5  25 kg  9,8
m
s2
 122,5N
Si aplicamos ahora la 2ª ley de Newton, F – Fr = m  a
Y despejamos la aceleración,
a
F - Fr 130 N - 122,5N 7,5 N
N


 0,3  0,3 m/s2
m
25 kg
25 kg
kg
Para calcular la velocidad a los 10 segundos de haber empezado a actuar la fuerza de arrastre,
basta con aplicar la ecuación de la velocidad para un movimiento uniformemente acelerado (aceleración
constante), teniendo en cuenta que como parte del reposo, la velocidad inicial es 0,
v  v 0  a  t  0  0,3
m
s2
 10 s  3 m/s
Finalmente, para calcular el espacio recorrido en esos 10 segundos, aplicamos la ecuación de la
distancia para el movimiento uniformemente acelerado,
1
1
m
1
s  s 0  v 0  t   a  t 2  0  0   0,3 2  (10s)2   0,3  100 m  15 m
2
2
2
s
fisicayquimica.com
La gráfica de la velocidad frente al tiempo es
v / m/s
3
2
1
t/s
0
0
1
2
3
4
5
6
7
fisicayquimica.com
8
9
10
La gráfica de la distancia frente al tiempo es
s/m
15
10
5
0
1
2
3
4
5
t/s
1
2
3
4
5
6
7
8
6
7
s/m
0,15
0,60
1,35
2,40
3,75
5,4
7,35
9,6
fisicayquimica.com
8
9
10
9
10
12,15
15
2. Explica por qué cuando un coche gira hacia un lado, las personas en el interior se deslizan hacia el lado
contrario (1 punto)
Porque el cuerpo tiende a seguir la trayectoria recta (principio de inercia). Por eso cuando el coche
gira a la derecha, las personas tienden a seguir la trayectoria recta (en este caso a la izquierda), y de forma
similar, las personas tienden a inclinarse hacia la derecha cuando el coche gira a la izquierda.
3. Enuncia las leyes de Newton y pon un ejemplo de cada una (2 puntos)
1ª ley o principio de inercia, indica que todo cuerpo permanece en estado de reposo o en movimiento
rectilíneo y uniforme mientras no actúe sobre él una fuerza neta (tendencia de las personas en un vehículo
a seguir hacia delante cuando éste frena)
2ª ley o principio fundamental de la dinámica, indica que la aceleración de un cuerpo es proporcional a la
fuerza resultante ejercida sobre el mismo, con la misma dirección y sentido que dicha fuerza, e
inversamente proporcional a la masa del cuerpo,
a
F
m
Cuanto mayor sea la fuerza aplicada, mayor es la aceleración producida (si no varía la masa), y cuanto
mayor es la masa, más fuerza hay que comunicar para conseguir la misma aceleración.
3ª ley o principio de acción y reacción, indica que cuando dos cuerpos interaccionan, las fuerzas que
ejercen el uno sobre el otro tienen idéntico módulo y dirección, pero sentidos opuestos (cuando un patinador
en reposo empuja a otro en igual estado, los dos retroceden)
4. Un coche de 1200 kg que va a 90 km/h es capaz de frenar en 2,5 s. Calcula la fuerza empleada para frenar
al coche y la distancia recorrida hasta parar (2 puntos)
Lo primero que debemos hacer es pasar la velocidad a unidades del S.I., es decir, a m/s.
90
km 1000 m
1h
90  1000 m



 25 m/s
h
1 km
3600 s
3600 s
La aceleración la podemos despejar de la ecuación de la velocidad para el movimiento uniformemente
acelerado,
v  v0  a  t  a 
v - v 0 0 - 25 m/s

  10 m/s2
t
2,5 s
fisicayquimica.com
Si aplicamos ahora la 2ª ley de Newton, F = m  a = 1200 kg × (- 10 m/s2)= - 12000 N
Finalmente, para calcular el espacio recorrido en esos 2,5 segundos, aplicamos la ecuación de la
distancia para el movimiento uniformemente acelerado,
1
1
m
s  s 0  v 0  t   a  t 2  0  25 m/s  2,5 s   ( 10 2 )  (2,5 s) 2  62,5 m  31,3 m  31,2 m
2
2
s
5. Completa la siguiente tabla (4 puntos)
Marte
Venus
Masa / kg
6,4191 × 1023
4,8690× 1024
Radio / km
3.397,00
6.051,59
Periodo de rotación / días
1,02595675
243,0187
Distancia al Sol / km
227.936.640
108.208.930
Periodo orbital / años
1,8808476
0,61519726
Velocidad orbital
24,145 km/s
35,045 km/s
Velocidad en el ecuador
867 km/h
6,52 km/h
gravedad
3,71 m/s2
8,87 m/s2
Peso de una persona de 60 kg
222,6 N
532,2 N
Masa aparente en la Tierra
22,7 kg
54,3 kg
2
r
T
En el caso de la velocidad orbital de Marte en torno al Sol hay que tomar la distancia de dicho planeta al
Sol y el periodo orbital, teniendo en cuenta que la distancia debe estar en metros y el periodo en segundos,
Para calcular la velocidad orbital debemos tener en cuenta que v  r 
v  r 
2
r 
T
2
m
km
 227936640000m  24145  24,145
días
hora
segundos
s
s
1,8808476años  365
 24
 3600
año
día
hora
Para calcular la velocidad en un punto del ecuador, hay que usar la misma fórmula, pero el periodo será
el de rotación y la distancia será el radio,
v  r 
2
r 
T
2
m 1km 3600s
km
 3397000m  240,7 

 867
segundos
horas
s 1000m
1h
h
1,02595675días  24
 3600
día
hora
fisicayquimica.com
Para calcular la gravedad, sabemos que en la superficie terrestre el peso coincide con la fuerza
gravitatoria,
GMm
GM
P  mg 
g 2
2
R
R
Por tanto, sustituyendo la masa de Marte y su radio, tenemos que
g
GM
R2

6,67  10 11Nm2 kg2  6,4191 1023 kg
(3,397  106 m) 2
 3,71
m
s2
El peso de una persona se calcula multiplicando su masa por la gravedad, por lo que
P = m  g = 60 kg  3,71 m/s2 = 222,6 N
Y la masa equivalente en la Tierra se obtiene dividiendo su peso en Marte por la aceleración de la
gravedad de la Tierra, 9,8 m/s2,
P
222,6N
m eq  Marte 
 22,7kg
m
g Tierra
9,8 2
s
Para el planeta Venus hacemos lo mismo. En el caso de su velocidad orbital en torno al Sol hay que
tomar la distancia de dicho planeta al Sol y el periodo orbital, teniendo en cuenta que la distancia debe estar
en metros y el periodo en segundos,
v  r 
2
r 
T
2
m
km
 108208930000m  35045  35,045
días
hora
segundos
s
s
0,61519726años  365
 24
 3600
año
día
hora
Para calcular la velocidad en un punto del ecuador, hay que usar la misma fórmula, pero el periodo será
el de rotación y la distancia será el radio,
v  r 
2
r 
T
2
m 1km 3600s
km
 6051590m  1,81 

 6,52
segundos
horas
s 1000m
1h
h
243,0187días  24
 3600
día
hora
Para calcular la gravedad, sustituyendo la masa de Venus y su radio, tenemos que
g
GM
R2

6,67  10 11Nm2 kg2  4,8690  1024 kg
(6051590m) 2
 8,87
m
s2
El peso de una persona se calcula multiplicando su masa por la gravedad, por lo que
P = m  g = 60 kg  8,87 m/s2 = 532,2 N
Y la masa equivalente en la Tierra se obtiene dividiendo su peso en Venus por la aceleración de la
gravedad de la Tierra, 9,8 m/s2,
P
532,2N
m eq  Venus 
 54,3kg
m
g Tierra
9,8 2
s
fisicayquimica.com
fisicayquimica.com