mecanismos 2013

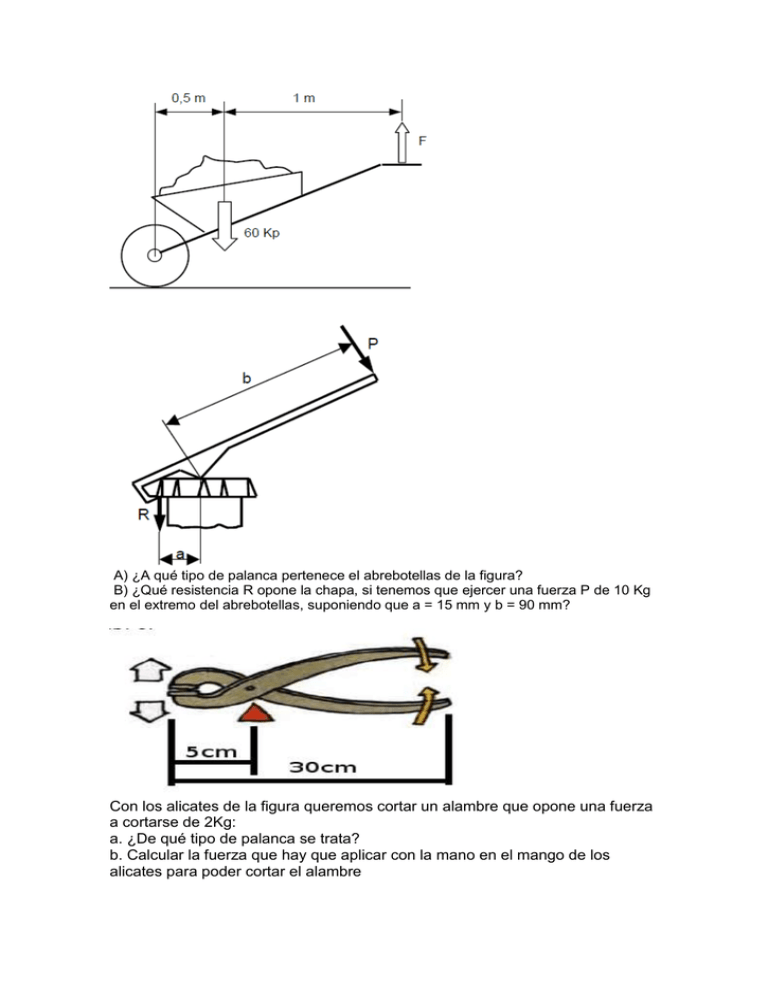
A) ¿A qué tipo de palanca pertenece el abrebotellas de la figura?
B) ¿Qué resistencia R opone la chapa, si tenemos que ejercer una fuerza P de 10 Kg
en el extremo del abrebotellas, suponiendo que a = 15 mm y b = 90 mm?
Con los alicates de la figura queremos cortar un alambre que opone una fuerza
a cortarse de 2Kg:
a. ¿De qué tipo de palanca se trata?
b. Calcular la fuerza que hay que aplicar con la mano en el mango de los
alicates para poder cortar el alambre
En el momento de la pesca estábamos agarrando la caña por los
puntos “F” y “A” ¿Qué esfuerzo tuvimos que realizar para
levantar el pez?
Si la posición de las manos fuera la misma, pero estuviéramos
empleando una caña de pescar de 5 m de longitud ¿Qué
esfuerzo tendríamos que realizar?
Con los alicates de la figura se quiere cortar un cable que opone una resistencia equivalente a
2 Kg. Responde a las siguientes preguntas:
a) ¿De qué grado es la palanca mostrada?
b) Calcular la fuerza que tendremos que aplicar para cortar el cable con los alicates.
¿Qué esfuerzo tenemos que hacer si sujetamos la pala por los
puntos “F” y “B”?
¿Por qué puntos tendríamos que sujetamos la pala para realizar el
mínimo esfuerzo?
Tenemos una balanza
romana con una pesa (potencia) de 500 g y una carga (resistencia) de 2 Kg. La
distancia entre el punto de aplicación de la resistencia y el fiel de la balanza
(fulcro) es de 100 mm.
¿A qué distancia del fiel (BP, brazo de potencia) hemos de
colocar la “pesa” para equilibrar la balanza?
Calcula las velocidades de giro de las siguientes poleas
d1= 20 cm d2= 30 cm n2= 1200 rpm
Motor gira a 1800 rpm
Za=10
Zb=50
B=C
Zc=15
Zd?
El motor de una lavadora está unido a una polea de 8 cm de diámetro, mientras que el
bombo lo está a una polea de 32 cm. La velocidad máxima de giro del bombo al centrifugar
es de 1200 rpm. ¿A qué velocidad debe girar el motor?
Calcular las relaciones de transmisión, y la velocidad
de las siguientes ruedas sabiendo que la velocidad de
giro de la rueda 1 gira a una velocidad de 100 rpm.
d1= 10 cm d2= 20 cm d3= 15 cm d4= 30 cm
La figura muestra el sistema de poleas de un taladro. Según la combinación de poleas que
elijamos podemos utilizar diferentes velocidades de giro de la broca.
a) ¿Con qué combinación de poleas obtendremos la velocidad mínima de giro de la broca?
b) ¿Con qué combinación de poleas obtendremos la velocidad máxima de giro de la broca?
c) Si el motor gira a 1400 rpm, ¿cuál es la velocidad mínima a la que puede girar la broca?
En la siguiente figura se muestra un mecanismo en el que el engranaje motriz gira a 800 rpm
(engranaje 4). Calcular las relaciones de transmisión y la velocidad de giro de cada uno de los
engranajes
En la figura se muestra un exprimidor de fruta. El eje del motor, que
mueve un engranaje de 10 dientes gira a 1800 rpm.
a) Si la rueda B posee 50 dientes, ¿a qué velocidad girará?
b) La rueda C de 15 dientes gira solidariamente con la rueda B. ¿A qué
velocidad girará la rueda D de 45 dientes?
En el mecanismo simple de transmisión por poleas de la figura el eje A
gira a 3000 rpm, D1= 20 mm y D2= 60 mm: a)
Calcula la velocidad de giro del eje B; b) Si
aumentamos la velocidad de giro del eje A
hasta 6000 rpm, ¿qué valor debería tener D1
para que el eje B siga girando a la misma velocidad
que en el caso anterior?; c) Calcula la
relación de transmisión Rt correspondiente a
10 N R = 5 N este último caso.
24.En la máquina de la figura (que es
una fresadora), el motor gira a 1500
rpm y en su eje está acoplada una
polea de diámetro 100 mm. Ésta
trasmite el movimiento a otro eje a
través de otra polea de diámetro 300
mm. En este segundo eje hay tres
ruedas dentadas y solo engrana una
de ellas cada vez con las del eje
siguiente. Engrana la de 40 dientes
con la de 25 dientes, o la de 44
dientes con la de 22 dientes o la de
36 dientes con la de 30 dientes. En
este mismo eje hay otras dos ruedas
dentadas que también engranan una
de ellas con las del cuarto y último
eje. Engrana la de 30 dientes con la
de 62 dientes o la de 46 dientes con
la de 46 dientes. Calcular:
2.1.- En el sistema de poleas de
la figura ¿A que velocidad girará el eje conducido si el conductor lo hace a 250 r.p.m.?
Si el motor gira a 1400 rpm ¿Cuál es la mínima velocidad que se
puede obtener en la broca?
Si se elige la posición que aparece representada en la figura ¿A
qué velocidad girará la broca?
Dado el sistema de engranajes de la figura y sabiendo que z = 20 , z = 40 , z =
1
2
3
20 , z = 60 , y la velocidad de la rueda 1 es n = 600 rpm; calcula las
4
velocidades de las ruedas 2, 3 y 4.
1