FORMULACION DE BALISTICA EXTERIOR

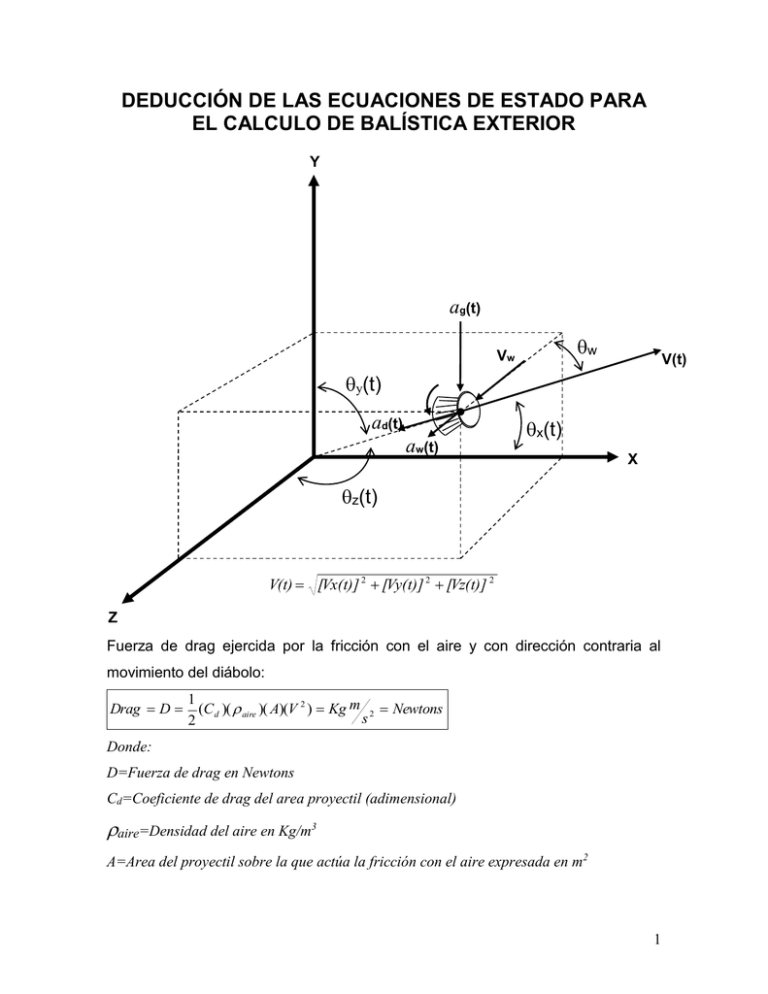
DEDUCCIÓN DE LAS ECUACIONES DE ESTADO PARA
EL CALCULO DE BALÍSTICA EXTERIOR
Y
ag(t)
w
Vw
V(t)
(t)
y(t)
(t)
ad(t)
aw(t)
x(t)
(t)
X
z(t)
(t)
V(t)  [Vx(t)] 2  [Vy(t)] 2  [Vz(t)] 2
Z
Fuerza de drag ejercida por la fricción con el aire y con dirección contraria al
movimiento del diábolo:
Drag  D 
1
(C d )(  aire )( A)(V 2 )  Kg m 2  Newtons
s
2
Donde:
D=Fuerza de drag en Newtons
Cd=Coeficiente de drag del area proyectil (adimensional)
aire=Densidad del aire en Kg/m3
A=Area del proyectil sobre la que actúa la fricción con el aire expresada en m2
1
V=Velocidad del proyectil en m/s
Como la fuerza es igual al producto de la masa y la aceleración, tenemos que:
F  (m)(a)
a
F
m
A partir de ésta última ecuación obtenemos la desaceleración del diábolo a causa
de la fricción con el aire expresada en m/s2 :
ad  
 
C   A V 2
D
  d aire
mp
2m p
(Negativa por ser desaceleración)
Donde mp representa la masa del proyectil expresada en Kg.
Escribiendo ésta ecuación en función del tiempo obtenemos la siguiente
expresión:
ad
2

Cd t aire t V t   A
t   
2m p
De igual forma y debido a la velocidad del viento, se produce una aceleración en el
diábolo que está dada por:
2

Cd w t  aire t Vw   Aw 
aw t  
2m p
2
Donde:
aw(t)=Aceleración provocada por el viento en el proyectil en m/s2
Cdw(t)=Coeficiente de drag del area del proyectil donde golpea el viento en función del
tiempo y que tiene un valor adimensional
Aw=Area del proyectil sobre la que actúa el viento expresada en m2
Vw=Velocidad del viento en m/s
Debido a que el diábolo se mueve en tres dimensiones, haremos la
descomposición de las aceleraciones y desaceleración del proyectil en sus
componentes vectoriales como una función del tiempo:
2

Cd t  aire t V t   A
ad t x  
Cos x 
2m p
2

Cd t  aire t V t   A
ad t  y  
Cos y   a g t 
2m p
2

Cd t  aire t V t   A
ad t z  
Cos z   aw t 
2m p
Donde:
ag(t)=Aceleración de la gravedad como una función del tiempo expresada en m/s2
aw(t)=Aceleración
provocada en el proyectil debido a la velocidad del viento
expresada como una función del tiempo en m/s2
Si expresamos la aceleración como la primera derivada de la velocidad con
respecto al tiempo, las componentes vectoriales de la aceleración del diábolo
pueden escribirse como:
3
dV t x
C t  aire t V t   A Cos 
 d
x
dt
2m p
2
dV t  y
dt
2

Cd t  aire t V t   A

Cos y   a g t 
2m p
C t  aire t V t   A Cos   a t 
dV t z
 d
z
w
dt
2m p
2
Rescribiendo las ecuaciones:
dV t x
C t  aire t V t  AV t Cos 
 d
x
dt
2m p
dV t y
dt

Cd t aire t V t  AV t Cos  a t 
y
g
2m p
C t  aire t V t  AV t Cos   a t 
dV t z
 d
z
w
dt
2m p
Si
sustituímos
las
expresiones
Vx t   V t Cos x  ,
Vy t   V t Cosy  ,
Vz t   V t Cosz , V(t)  [V x(t)] 2  [V y (t)] 2  [V z (t)] 2 , las tres ecuaciones de
aceleración anteriores quedan escritas de la siguiente forma:
dV t x
C t  aire t Vx t  A [V (t)]2  [V (t)]2  [V (t)]2
 d
x
y
z
dt
2m p
dV t y
dt

Cd t  aire t Vy t  A
2m p
[V x(t)]2  [V y(t)]2  [V z(t)]2  a g t 
C t  aire t Vz t  A [V (t)]2  [V (t)]2  [V (t)]2  a t 
dV t z
 d
x
y
z
w
dt
2m p
Resolviendo el sistema anterior encontramos las ecuaciones para la solución de
velocidades en “X”, “Y” y “Z”. Integrando nuevamente las ecuaciones resultantes,
4
encontraremos las ecuaciones para la solución de desplazamiento del diábolo en
“X”, “Y” y “Z”. Se debe tener cuidado de sustituír las condiciones iniciales correctas
del sistema de ecuaciones al momento de realizar las integraciones.
5