ONDA PERIÓDICA

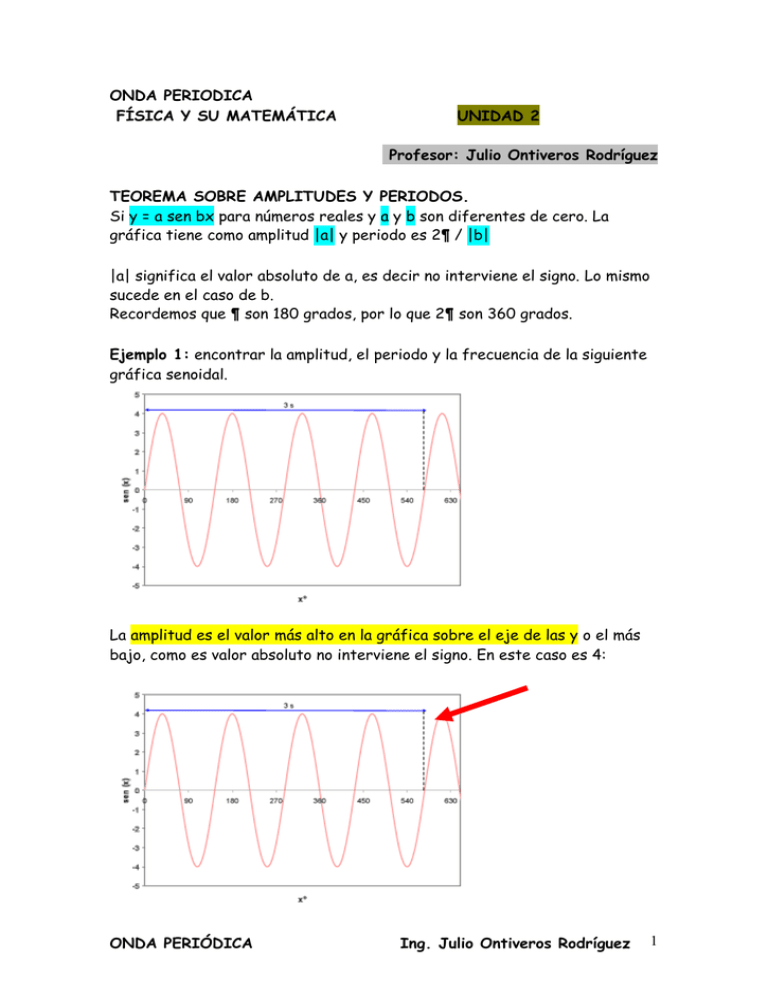
ONDA PERIODICA
FÍSICA Y SU MATEMÁTICA
UNIDAD 2
Profesor: Julio Ontiveros Rodríguez
TEOREMA SOBRE AMPLITUDES Y PERIODOS.
Si y = a sen bx para números reales y a y b son diferentes de cero. La
gráfica tiene como amplitud |a| y periodo es 2¶ / |b|
|a| significa el valor absoluto de a, es decir no interviene el signo. Lo mismo
sucede en el caso de b.
Recordemos que ¶ son 180 grados, por lo que 2¶ son 360 grados.
Ejemplo 1: encontrar la amplitud, el periodo y la frecuencia de la siguiente
gráfica senoidal.
La amplitud es el valor más alto en la gráfica sobre el eje de las y o el más
bajo, como es valor absoluto no interviene el signo. En este caso es 4:
ONDA PERIÓDICA
Ing. Julio Ontiveros Rodríguez
1
El periodo por definición es 2¶ / |b| sabemos que el periodo es un ciclo
completo de la onda, en el caso del péndulo un viaje de ida y vuelta.
Observa una onda completa: A0 es la amplitud y T el periodo.
En este ejemplo podemos contar 2 y media ondas completas en 3600
2.5 ondas son 3600 = 2¶ al despejar el periodo b = 2.5
Como y = a sen bx
La ecuación se escribe: y = 4 sen 2.5 x
La frecuencia es el número de ondas completas por segundo.
En este caso contamos 4 ondas completas en tres segundos. La frecuencia
es 4/3= 1.333333…
Es un número periódico por lo que el 333 continua
hasta el infinito.
La longitud de onda se abrevia con la letra griega lambda
λ y es la distancia
entre dos crestas o dos valles consecutivos.
ONDA PERIÓDICA
Ing. Julio Ontiveros Rodríguez
2
Ejemplo 2: encontrar la amplitud, el periodo y la frecuencia de la siguiente
gráfica senoidal.
La amplitud es 2.5 como lo señala la flecha. Por lo que
a = 2.5
El periodo lo obtenemos contando las ondas completas en 360 grados en
este caso son 6 ondas completas por lo que b = 6
Para verificar y saber que hacer si no se ven los 3600 en la gráfica,
observamos que en 90 grados hay 1.5 ondas por regla de tres,
90
1 .5

360
x
al
despejar obtenemos el 6 como resultado.
Como y = a sen bx
La ecuación nos queda y = 2.5 sen 6x
La frecuencia la obtenemos contando las ondas completas dentro del
intervalo de tiempo que nos señala la flecha, en esta gráfica hay 5 ondas
completas en un segundo, f = 5 Hz.
ONDA PERIÓDICA
Ing. Julio Ontiveros Rodríguez
3
Ejemplo 3: encontrar la amplitud, el periodo y la frecuencia de la siguiente
gráfica senoidal. Practica anotando las respuestas en los espacios
correspondientes.
En este caso la amplitud es __ como nos lo muestra la flecha.
a = __
El periodo lo obtenemos contando las ondas completas en 360 grados.
Hay ___ondas completas en 3600, como 3600 es igual a 2¶ al despejar nos
queda 2¶/__ = 2¶ / |b| por observación b = ___
La ecuación original y = a sen bx al ser sustituida queda:
y = _sen _x
Para calcular la frecuencia contamos las ondas completas dentro de los 2
segundos, son __ ondas completas. Por lo que la frecuencia es __ ondas
completas en 2 segundos es decir __ ondas por segundo lo que equivale a __
Hz.
ONDA PERIÓDICA
Ing. Julio Ontiveros Rodríguez
4