Resumen campo eléctrico

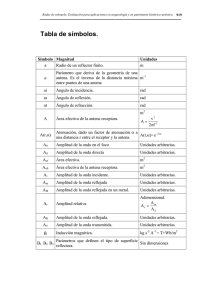
Cuadro resumen campo eléctrico
Ley de Coulomb
La interacción entre dos partículas cargadas es proporcional a sus cargas e inversamente proporcional al cuadrado de la
distancia entre ellas, siendo su dirección la de la recta que las une.
F=Ke
q1 q2
r
2
indicando su carácter vectorial
F=K e
q1 .q 2
ur
r2
u r vector unitario dirigido de la carga q 1 a la carga q2. ke = 9 • 109 N m2/C2 k e =
1
4πε 0
ε0 constante dieléctrica o permitividad eléctrica del vacío, de valor: 8'854 • 10 -12 C 2 /(N • m 2 )
ε= εr.ε0 la constante dieléctrica o permitividad del medio y εr la constante dieléctrica relativa o coeficiente dieléctrico .
El valor de εr es siempre mayor que uno.
Descripción vectorial del campo eléctrico Intensidad del campo eléctrico
F
q
E= =ke 2 u r
q'
r
definida en un punto como la fuerza por unidad de carga positiva colocada en dicho punto
La intensidad del campo eléctrico, en el SI, se mide en «newton por culombio», de símbolo N/C. esta unidad equivale a
«voltio por metro» (V/m).
Cuando varias cargas están presentes, en virtud del principio de superposición, la intensidad del campo eléctrico
resultante es la suma vectorial de las intensidades del campo eléctrico debidas a cada carga por separado.
Fuerza sufrida por cargas en un campo constante homogéneo e isótropo
Descripción escalar del campo eléctrico Energía potencial eléctrica
F = q'E
La fuerza sobre q es F  qE sabemos que se trata de una fuerza conservativa. WFe A→B (camino 1) = WFe A→B (camino 2)
Esta expresión es diferente para cada tipo de fuerza conservativa, pero en cualquier caso se trata de una energía
potencial Ep. Podemos escribir:
WFelectrica i→f = -ΔEp = -(Epf-Epi)
WFext i→f = +ΔEp = (Epf-Epi)
Potencial eléctrico. Diferencia de potencial
E p (r)
;
ΔEp= q ΔV;
V(r)=
q
V(r) = ke Q/r
el potencial eléctrico representa el trabajo realizado, contra las fuerzas del campo, para llevar la unidad de carga positiva
desde el nivel de referencia hasta el punto considerado
Potencial eléctrico de una carga puntual V=ke Q
r
qi
Potencial eléctrico de una distribución discreta de cargas V =k
T
e
ri
Potencial eléctrico de un campo eléctrico uniforme E=E0 i(N/C) E=-
ΔV
d
Superficies equipotenciales
 Cuando una carga se desplaza sobre una misma superficie equipotencial, el trabajo realizado sobre la misma es cero.
W(A_B) = —(EPB — EpA) = — q(Vs — VA) = 0, ya que VA = VB.
 La dirección del campo eléctrico es perpendicular a la superficie equipotencial en cada uno de sus puntos. Se deduce de lo
B
anterior; si WAB =q E. ds=0,

A
y E es perpendicular a
entonces E.ds=0
dr , siendo dr un elemento infinitesimal medido sobre la superficie equipotencial.