geometría - guia nº5

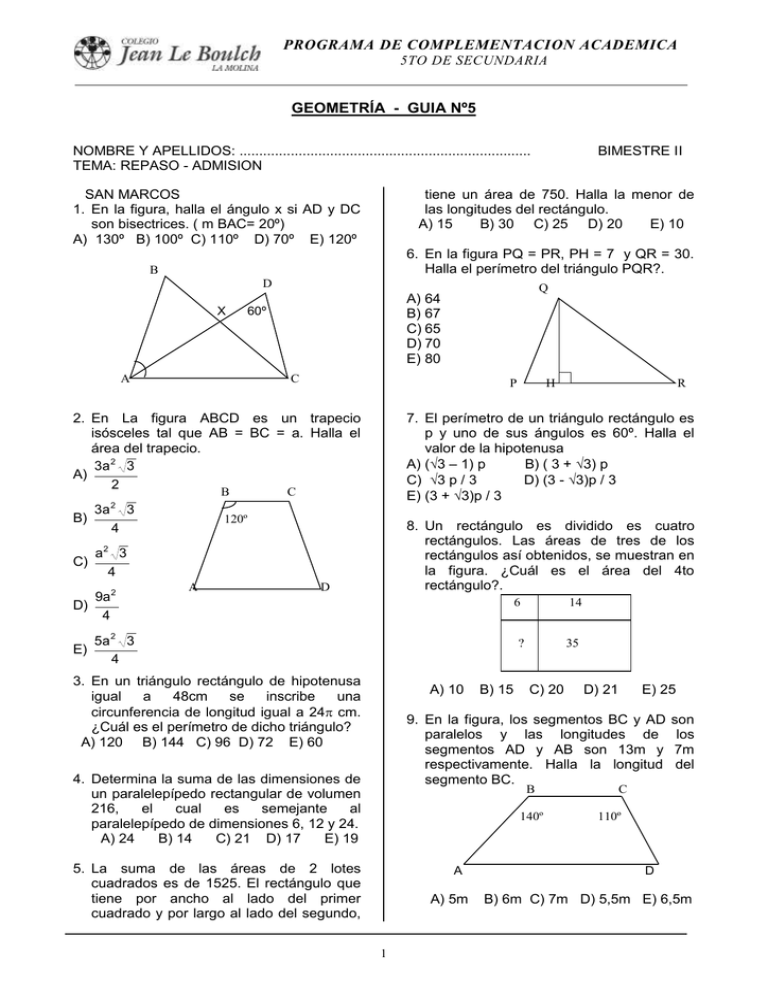
PROGRAMA DE COMPLEMENTACION ACADEMICA
5TO DE SECUNDARIA
GEOMETRÍA - GUIA Nº5
NOMBRE Y APELLIDOS: ..........................................................................
TEMA: REPASO - ADMISION
SAN MARCOS
1. En la figura, halla el ángulo x si AD y DC
son bisectrices. ( m BAC= 20º)
A) 130º B) 100º C) 110º D) 70º E) 120º
tiene un área de 750. Halla la menor de
las longitudes del rectángulo.
A) 15
B) 30 C) 25 D) 20
E) 10
6. En la figura PQ = PR, PH = 7 y QR = 30.
Halla el perímetro del triángulo PQR?.
B
D
X
A
60º
C
B
3a 2 3
B)
4
P
E)
C
120º
A
H
R
7. El perímetro de un triángulo rectángulo es
p y uno de sus ángulos es 60º. Halla el
valor de la hipotenusa
A) (3 – 1) p
B) ( 3 + 3) p
C) 3 p / 3
D) (3 - 3)p / 3
E) (3 + 3)p / 3
8. Un rectángulo es dividido es cuatro
rectángulos. Las áreas de tres de los
rectángulos así obtenidos, se muestran en
la figura. ¿Cuál es el área del 4to
rectángulo?.
a2 3
4
9a 2
D)
4
Q
A) 64
B) 67
C) 65
D) 70
E) 80
2. En La figura ABCD es un trapecio
isósceles tal que AB = BC = a. Halla el
área del trapecio.
3a 2 3
A)
2
C)
BIMESTRE II
D
5a 2 3
4
3. En un triángulo rectángulo de hipotenusa
igual
a
48cm
se
inscribe
una
circunferencia de longitud igual a 24 cm.
¿Cuál es el perímetro de dicho triángulo?
A) 120 B) 144 C) 96 D) 72 E) 60
A) 10
B) 15
6
14
?
35
C) 20
D) 21
E) 25
9. En la figura, los segmentos BC y AD
paralelos y las longitudes de
segmentos AD y AB son 13m y
respectivamente. Halla la longitud
segmento BC.
4. Determina la suma de las dimensiones de
un paralelepípedo rectangular de volumen
216,
el
cual
es
semejante
al
paralelepípedo de dimensiones 6, 12 y 24.
A) 24
B) 14
C) 21 D) 17
E) 19
B
140º
5. La suma de las áreas de 2 lotes
cuadrados es de 1525. El rectángulo que
tiene por ancho al lado del primer
cuadrado y por largo al lado del segundo,
A
A) 5m
1
son
los
7m
del
C
110º
D
B) 6m C) 7m D) 5,5m E) 6,5m
respectivamente. Si la razón entre A1 y
A2 es 4, entonces (p1 /p2 )2 es:
10. En la figura, halla el ángulo , si x - y =
50º
A) 2
B) 4
C) 8
D) 16
E) 3
15. En el rectángulo ABCD de la figura, la
longitud de los segmentos AB y FC son
respectivamente 2 y 4m. Si los
segmentos AE y EM son iguales. ¿Cuál
es el perímetro
D del rectángulo?.
C
X


y

F
M
A) 70º B) 65º C) 80º D)100º
E) 75º
E
11. Se tiene un hexágono regular de 2m de
lado. Se construyen circunferencias de
1m de radio, tangentes exteriores cada
lado en su punto medio. ¿Cuál es el área
en m2 del hexágono obtenido al unir los
centros de cada circunferencia?.
A) 9 + 3
B) 9 + 3 3
D) 12 + 4 3


A
A) 48
C) 12 + 8 3
E) 9 + 6 3
C
D) 24
E) 28
17. Si la circunferencia rueda hacia la
derecha, desde la posición indicada en la
figura. ¿Qué longitud recorrerá hasta que
el punto B toque la superficie por tercera
vez?.
30º
O
C) 36
16. En un triángulo rectángulo cuya
hipotenusa mide 48cm. se inscribe una
circunferencia de longitud 24cm. ¿Cuál
es el perímetro de dicho triángulo?
U.N.M.S.M. – 1999
a) 120cm.
c) 96cm.
e) 60cm.
b) 144cm.
d) 72cm.
12. En la figura, el segmento AB es un
diámetro y la longitud del segmento AC
es 4m. El área de la región sombreada
en m2 es:
A
B) 30
B
B
B
A) 4 - 3 3
D) 2 - 3 2
B) 2 - 3 3
C) 4 - 3 2
2/3
E) 3 - 2 3
5
13. Un cilindro circular recto está inscrito en
un cubo de arista 2a. El volumen del
cilindro es 16. Halla el volumen del
cubo.
A) 32
B) 100
C) 8
D) 80
O
A
A) 10/3 B) 40 C) 100/3 D) 20 E) 80/3
E) 64
14. Dos triángulos equiláteros de perímetros
p1 y p2 tienen áreas A1 y A2
2
U. DE LIMA
18. En la figura, el triángulo ABC es
equilátero y MN// AC , hallar el área de
la región sombreada.
21. De un punto A, exterior a un círculo, se
trazan secantes AB yAC que cortan a la
circunferencia en D y E. Se un B con E.
Si el ángulo DBE = 40º y el ángulo BEC
= 62º. Halla el ángulo BAC.
A) 18º B) 19º C) 21º D) 22º E) 20º
B
M
N
22. En un polígono se cumple que 8 veces el
cuadrado del número de lados excede
en 272 a la suma de sus ángulos
internos. ¿Cuántos lados tiene el
polígono?
A) 19 B) 22 C) 20 D) 21 E) 18
10m.
A
C
12m.
a)
4 3m
2
c)
U.N.M.S.M. – 2002
e) 9 3m2
6 3m2
b)
3 3m2
d)
8 3m2
23. El segmento perpendicular a un diámetro
desde un punto de la circunferencia mide
12. Si uno de los segmentos que
determina sobre el diámetro mide 4.
Halla el radio de la circunferencia.
A) 10
B) 20 C) 15 D) 25 E) 5
19. En la figura “P”, “Q” y “T” son puntos de
tangencia, “a“ y “b” son los radios de las
semicircunferencias.
Determinar
la
distancia del punto “T” a la recta PQ .
24. El perímetro de un triángulo mide 20cm.
Si el lado mayor excede en 6 al lado
menor y el intermedio es doble del
menor más 2cm. ¿Cuánto mide el lado
mayor?
A) 5cm
B) 7cm
C) 9cm
D) 11cm
E) 13cm
P
Q
a
b
O1
a) 2 ab
b)
2ab
T
O2
25. ¿Cuántos lados tiene el polígono cuyo
número de diagonales excede en 4 al
número de diagonales de un pentágono?
A) 6
B) 4 C) 7 D) 8 E) 9
U.N.M.S.M. – 2001
2ab
2ab
c)
e)
ab
ab
ab
d)
ab
20. En un hexágono regular de lado “L” se
unen los puntos medios de cuatro lados
opuestos dos a dos. Luego se unen los
puntos medios de los lados del
rectángulo que se formo, obteniéndose
un cuadrilátero. Hallar el área de este
cuadrilátero.
U.N.M.S.M. – 1999
a)
c)
e) 3 3 2
3 2
3 3 2
L
L
L
8
4
8
b)
d)
3 2
3 2
L
L
4
2
3
GEOMETRÍA - GUIA Nº6
NOMBRE Y APELLIDOS: ..........................................................................
TEMA: GEOMETRIA DEL ESPACIO I

La geometría del espacio es la rama de la
geometría que se ocupa de las propiedades y
medidas de las figuras geométricas en el
espacio tridimensional o espacio euclídeo.
Entre estas figuras, también llamadas
sólidos, se encuentran el cono, el cubo, el
cilindro, la pirámide, la esfera, el prisma, los
poliedros regulares y otros poliedros.
1.
POSICIONES
PLANOS

Planos paralelos: Cuando no tienen
algún punto en común


RELATIVAS
DE
2
BIMESTRE II
Recta y plano paralelos: Cuando no
tienen ningún punto en común.

Recta y plano secantes: Cuando tienen
un punto en común llamado punto de
intersección.

Recta contenida en un plano: Cuando
todos los puntos de la recta están
contenidos en el plano.

Teorema de Thales
Planos secantes: Cuando tienen una
recta en común llamada recta de
intersección.
Planos coincidentes: Cuando todos los
puntos de uno de ellos pertenecen al
otro.
A
D
E
B
C
2.
POSICIONES RELATIVAS
RECTA Y UN PLANO.
AB DE

BC EF
DE UNA
4
F

L1
Proyecciones: La proyección del
segmento AB sobre el plano P, es el
segmento AD, siendo BD perpendicular
al plano P.
L2
B
Θ
M
N
P
D
A
P
ANGULOS DIEDROS

3.
Ángulo entre una recta y un plano: Es
el ángulo entre la recta y su proyección
sobre el plano. En la figura anterior es
el ángulo θ.
POSICIONES
RECTAS.
RELATIVAS
DE
Es aquel ángulo formado por 2 semiplanos.
Se llama arista del diedro a la recta común
AB y caras a cada uno de los semiplanos.
2
PARALELAS: No tienen
puntos comunes. Están
en un mismo plano.
SECANTES: Tienen un
punto en común y están
en un mismo plano.
ANGULO POLIEDRO
Un ángulo poliedro es la región del espacio
limitada por tres o más semirrectas con un
origen común, llamado vértice.
ALABEADAS O
CRUZADAS: Cuando no
se cortan y no se están
en un mismo plano
ANGULO ENTRE 2 RECTAS ALABEADAS.Para medir el ángulo entre 2 rectas
alabeadas, se trazan por u punto en el
espacio 2 rectas paralelas a las alabeadas y
se mide el ángulo entre ellas.
DISTANCIA MENOR ENTRE DOS RECTAS
ALABEADAS.Existe un único segmento perpendicular a
dos rectas alabeadas cuya longitud
representa la menor distancia entre dichas
rectas. En la figura la menor distancia entre
las rectas L1 y L2 es MN.
ANGULOS TRIEDROS
Son ángulos poliedros de 3 caras
PROPIEDADES:
(a) En todo triedro una cara es menor
que a suma de las otras dos, pero
mayor que la diferencia de las otras
mismas
5
(b) En todo triedro la suma de sus
diedros es menor que 540° y mayor
que 180°.
(c) En todo triedro, a mayor cara se
opone mayor diedro y viceversa.
CLASES:
o Triedro rectángulo: Cuando una de las
caras mide 90°
o Triedro birectángulo: Cuando dos de
sus caras miden 90°.
o Triedro trirrectángulo: Cuando sus 3
caras miden 90°
……………………………………………………
POLIEDROS O SÓLIDOS GEOMETRICOS
Un poliedro es la figura que limita una región del espacio mediante 4 o más regiones poligonales
planas.
POLIEDROS REGULARES.- Sólo existen 5, los cuales tienen aristas congruentes, ángulos
diedros congruentes y ángulos poliedros congruentes.
NOMBRE
CARAS
TETRAEDRO
4 TRIÁNGULOS
EQUILÁTEROS
EXAEDRO
N° ARISTAS
N° VERTICES
N° DE CARAS
POR VERTICE
6
4
3
6 CUADRADOS
12
8
3
OCTAEDRO
8 TRIÁNGULOS
EQUILÁTEROS
12
6
4
DODECAEDRO
12 PENTÁGONOS
REGULARES
30
20
3
ICOSAEDRO
20 TRIÁNGULOS
EQUILÁTEROS
30
12
5
6
AREA DEL CUBO:
A = 6a2
DIAGONAL DEL CUBO
d= a 3
ALTURA DE UN TETRAEDRO: h =
VOLUMEN DEL CUBO:
V = a3
a = arista
a 3
6
ALTURA DE UN OCTAEDRO h = a 2
PROBLEMAS
8.
En un cubo la suma de las distancias de
los vértices a una diagonal del cubo mide
46. halla el área total del cubo.
9.
Halla el área del polígono que se forma
al unir los centros de 2 caras laterales
opuestas y los centros de las bases de
un cubo, si la arista del cubo mide 2m.
1. ABCD es un cuadrado de 4m de lado. Se
eleva AF perpendicular al plano ABCD,
tal que AF = 4m. Halla FC.
2. Se tiene un triángulo equilátero ABC de
lado igual a 2m. Se traza BQ
perpendicular al triángulo. Si BQ mide
2m y M es punto medio de BC. Halla QM.
10. En un cubo de arista igual a 6 se forma
un polígono uniendo los centros de las
caras laterales. Halla el perímetro de
dicho polígono.
3. C es una circunferencia de centro O
contenida en plano H. P es un punto
exterior a H. Se trazan. PQ  H en Q y
luego QF tangente a C en F. Si :QF =6,
PO = 15 y PQ = 9. Halla el radio de C.
4.
11. Halla el coseno del ángulo que forman la
diagonal de un cubo con la diagonal de
una de sus caras.
P y Q son dos planos perpendiculares
según una recta CD. A, un punto de P y
B, un punto de Q. Se trazan AE  CD y
BF  CD. Si AE = 12, EF = 3 y BF = 4.
Halla AB.
12. Halla la distancia entre los baricentros de
dos caras contiguas de un tetraedro
regular de arista a.
5. B y C con puntos de un plano P. A es otro
punto externo a P. Los ángulos de AB y
AC con P miden 30º y 60º
respectivamente. Si AB = 6. Halla AC.
6.
Halla el área total de un tetraedro regular
si la suma de las longitudes de todas las
aristas es 36.
7.
En un cubo cuya arista mide 1m. Halla la
distancia del centro de una cara a
cualquiera de los vértices de la cara
opuesta.
7
PRISMAS.Es un poliedro, dos de cuyas caras son regiones poligonales congruentes y paralelas. Siendo las
caras laterales paralelogramos.
CLASES:
a.
Prismas rectos: Cuando las aristas laterales son perpendiculares a las bases
b.
Prismas oblicuos: Cuando las aristas laterales son oblicuas a las bases.
c.
Prismas Regular: Cuando el prisma es recto y sus bases son polígonos regulares.
AREA DE UN PRISMA
ORTOEDRO.- Es un prisma cuyas caras son
rectángulos.
ATOTAL = ALATERAL + ABASES
VOLUMEN DE UN PRISMA
V = ABASE . h
h = altura
PROBLEMAS
6.
1.
Halla el volumen de un prisma cuya
altura mide 5 m y la base es un rombo
cuyas diagonales miden 6 m y 8 m.
2.
Halla el volumen en m3 de un prisma
triangular que tiene de base un triángulo
rectángulo cuyos catetos miden 3 y 4
metros y la altura es de 6 m.
3.
Halla el área lateral en m2 de un prisma
triangular de 2,24 m de alto y cuya base
tiene 3,75 m de perímetro.
4.
5.
El desarrollo de la superficie lateral de un
prisma triangular regular tiene por
diagonal 8 cm y por altura 43 cm. Halla
el volumen del prisma.
8. Halla el volumen del sólido mostrado
Tres caras de un ladrillo rectangular
tienen áreas de 6, 8 y 10 cm2. Halla el
volumen del ladrillo.
El área total de un ortoedro es 144 uno
de los lados de la base es el doble del
otro e igual a la altura. Halla la diagonal
del ortoedro.
8
7.
Halla el volumen de un rectoedro si su
diagonal mide 45° con la base y forma
30° con una cara lateral. (altura= 6 )
8.
Un prisma recto tiene como base un
trapecio isósceles de bases 10 y 20 y
cuyos lados no paralelos miden 13. Halla
el área de la sección plana, cuyo plano
forma 60° con el plano de la base y pasa
por la base mayor del trapecio.
GEOMETRÍA - GUIA Nº7
NOMBRE Y APELLIDOS: ..........................................................................
TEMA: PIRAMIDES
TIPOS
Una pirámide recta es un tipo de pirámide
cuyas caras laterales son triángulos
isósceles. En este tipo de pirámides la recta
perpendicular a la base que pasa por el
vértice corta a la base en su centro.
BIMESTRE II
VOLUMEN DE LA PIRAMIDE:
V
AREA BASE xALTURA
3
AREA LATERAL DE UNA PIRAMIDE
REGULAR
AL = p . aP
Apotema
de la
pirámide
p = semiperímetro de la
base
aP
AREA TOTAL DE LA PIRAMIDE
Apotema
de la
base
aB
AT = AL + ABASE
Una pirámide oblicua es aquella en la que
no todas sus caras laterales son triángulos
isósceles.
TRONCO DE PIRAMIDE
El tronco de pirámide es un poliedro
comprendido entre la base de la pirámide y
un plano que corta a todas las aristas
laterales.
Si el plano es paralelo al plano de la base se
dice que el tronco es de bases paralelas.
La distancia entre las bases es la altura del
tronco. Un tronco de bases paralelas de una
pirámide regular está formado por dos bases,
polígonos regulares semejantes, y varias
caras laterales que son trapecios isósceles.
Las alturas de estos trapecios se llaman
apotemas de dichos troncos.
Una pirámide regular es una pirámide recta
cuya base es un polígono regular.
AREA TOTAL:
Una pirámide convexa tiene como base un
polígono convexo.
Una pirámide cóncava tiene como base un
polígono cóncavo.
P1, P2 son los perímetros de las bases, a la
apotema del tronco y B1, B2 las áreas de las
bases.
9
5.
Calcula la apotema de una pirámide
pentagonal regular de 630 m2 de área
lateral si la arista básica mide 9m.
6.
Un recipiente sin tapa tiene la forma de
una pirámide regular invertida, donde su
altura mide 3 pies y su base es un
hexágono inscrito de una circunferencia
de diámetro igual a 2 pies. Se desea
pintar 100 de estos recipientes por
dentro y por fuera, para lo cual se
utilizará pintura donde con un galón se
puede pintar 470 pies cuadrados.
Determine la cantidad de galones de esa
pintura que se necesitarán para pintar
los 100 recipientes.
7.
Calcular el área lateral, el área total y el
volumen del tronco de la pirámide
cuadrangular de aristas básicas 24 y 14
cm, y de arista lateral 13 cm.
8.
Las áreas de las bases de un tronco de
pirámide son 1 y 9. Calcula el área de la
sección transversal cuyas distancias a la
base menor y mayor están en relación
de 3 a 1 respectivamente.
9.
Si el volumen del cubo mostrado mide
27. Halla el volumen de la pirámide
inscrita.
VOLUMEN DEL TRONCO
PROBLEMAS
1.
Calcula el área lateral, total y el volumen
de una pirámide cuadrangular de 10 cm
de arista básica y 12 cm de altura.
2.
Calcula el área lateral, total y el volumen
de una pirámide hexagonal de 6 cm de
arista básica y 5 cm de arista lateral.
3.
El área lateral de una pirámide cuya
base es un hexágono regular mide 540.
El apotema mide 9. Halla el lado de la
base.
4.
Calcula el volumen de una pirámide
regular, si el apotema mide 15m y la
base es un triángulo equilátero cuyo lado
mide 183.
10. Calcula el volumen de una pirámide
cuadrangular regular de 2m de altura si
su área lateral es 45 m2 .
10
PROGRAMA DE COMPLEMENTACION ACADEMICA
5TO DE SECUNDARIA
GEOMETRÍA - GUIA Nº8
TEMA: CILINDRO
BIMESTRE II
Un cilindro de revolución el sólido generado
al rotar un rectángulo alrededor de uno de
sus lados.
TRONCO DE CILINDRO CIRCULAR RECTO
VOLUMEN :
V =  R2. gm
AREA LATERAL :
AL = 2R.gm
h
r
Nota: La tapa superior es una elipse A = Ra
o
cilindro recto: si el eje del cilindro es
perpendicular a las bases.
o
cilindro oblicuo: si el eje no es
perpendicular a las bases.
PROBLEMAS
1.
Halla el volumen de un cilindro recto, si
el área de base mide 64  y la altura mide
la mitad del diámetro de base?.
2. Calcular el radio de base, la superficie
total y el volumen de un cilindro; sabiendo
que el área de base es de 36  y la altura
mide 12 m.
VOLUMEN DEL CILINDRO
AREA LATERAL
AREA TOTAL
V = r2 h
3.
Hallar la superficie lateral de un cilindro
de 12 m de altura, cuya base es un
círculo de 3,5 m de radio.
4.
Un cilindro de 18 m de altura, tiene 540
de superficie lateral. ¿Cuál es la
superficie total?.
5. La superficie total de un cilindro es 132 y
la superficie lateral es 100. ¿Cuál es el
radio de cada base?.
6. Un cilindro tiene por altura la misma
longitud que la circunferencia de la base.
Si la altura mide 100m. Halla el área total
y el volumen.
AL = 2rh
7. Halla el área total y el volumen de un
cilindro de 5m de altura cuya base tiene
un radio igual a 2m.
AT = 2r(r + h)
11
8. Un vaso cilíndrico cuyo diámetro mide
20 y su altura 40, está lleno de agua. Si
se vierte el agua en otro vaso, cuyo
diámetro mide 40.¿Qué altura alcanzará
el agua?.
13. Un cilindro circular recto cuya altura es 4
m y el radio de su base mide R, al
aumentar la altura en 12 m, el volumen
aumenta en x m3 . Si el radio de la base
aumenta en 12 m, el volumen aumenta
en x m3 , calcular el valor de R.
9. Una probeta de 6 cm de radio se echan
cuatro cubitos de hielo de 4 cm de arista.
¿A qué altura llegará el agua cuando se
derritan?.
14. Un tanque cilíndrico de radio 23 y tiene
5/6 de su volumen con vino. Desde su
posición normal se inclina el tanque
hasta que el vino esté a punto de
derramarse. Halla el ángulo de
inclinación con la horizontal.
10. Un recipiente cilíndrico de 5 cm de radio y
10 cm de altura se llena de agua. Si la
masa del recipiente lleno es de 2 kg,
¿cuál es la masa del recipiente vacío?.
15. Halla el volumen del cilindro mostrado, si
tiene una perforación esférica.
11. Si la relación entre el volumen y el área
lateral de un cilindro de revolución es
1/4, calcular la medida de su altura, si el
área de la base es 3/2 del área lateral.
12. Se tiene un tronco de cilindro circular
recto, a = 2,5 cm ( ver figura en la página
anterior), y el área de una superficie
esférica inscrita en dicho tronco es de 9π
cm2 . Calcular el volumen del tronco del
cilindro.
12
PROGRAMA DE COMPLEMENTACION ACADEMICA
5TO DE SECUNDARIA
GEOMETRÍA - GUIA Nº9
TEMA: CONO
BIMESTRE II
Un cono recto es un sólido de revolución
generado por el giro de un triángulo
rectángulo alrededor de uno de sus catetos.
Al círculo conformado por el otro cateto se
denomina base
AREA TOTAL DEL CONO
AT  R( R  g )
TRONCO DE CONO
Se denominan:
o
Cono recto, si el vértice equidista de la
base circular
o
Cono oblicuo, si el vértice no equidista
de su base
o
Cono elíptico, si la base es una elipse.
Pueden ser rectos u oblicuos.
AREA LATERAL
AL   R1  R2 g
La generatriz de un cono es cada uno de los
segmentos cuyos extremos son el vértice y
un punto de la circunferencia de la base.
La altura de un cono es la distancia del
vértice al plano de la base. En los conos
rectos será la distancia del vértice al centro
de la circunferencia de la base.
AREA TOTAL
AT   R12  R22  R1  R2 g 
VOLUMEN DEL CONO
VOLUMEN
V  R 2 .h / 3
V
AREA LATERAL DEL CONO
AL  Rg
13
h 2
R1  R22  R1 R2 
3
PROBLEMAS
9.
1.
Halla el volumen de un cono de 6m de
altura sabiendo que su base tiene un
radio de 3m.
2.
Halla la generatriz de un cono sabiendo
que su base tiene un diámetro igual a
12m y su altura mide 8m.
3.
Halla el área lateral y el volumen de los
conos mostrados en la figura: (Las
distancias están en metros
A)
10. Halla el volumen de un cono de
revolución de área lateral A si la
distancia del centro de la base a una de
sus generatrices es d.
11. Para una fiesta, Luís ha hecho 10 gorros
de forma cónica con cartón. ¿Cuánto
cartón habrá utilizado si las dimensiones
del gorro son 15 cm de radio y 25 cm de
generatriz?.
B)
4
5
En un cono de revolución se toma un
punto de una generatriz, el cual dista 5, 3
y 10 del vértice, la altura y la base
respectivamente. Halla el volumen del
cono.
12. El radio de la base de un cono circular
recto mide R y su altura mide H. Halla la
altura del cilindro de mayor área lateral
inscrito en el cono.
25
7
13. Un cono circular recto puede inscribirse
en otro cono circular recto de volumen
constante dado, con los mismos ejes y
con el vértice del cono interior tocando la
base del cono exterior. ¿Cuál debe de
ser la razón entre sus alturas H/ h, para
que el cono inscrito tenga el volumen
máximo?.
4.
Calcula el área lateral, total y el volumen
de un cono cuya generatriz mide 13 cm y
el radio de la base es de 5 cm.
5.
Calcula el área lateral, total y el volumen
de un cono cuya altura mide 4 cm y el
radio de la base es de 3 cm.
6.
Calcula el área lateral, el área total y el
volumen de un tronco de cono de radios
6 y 2 cm, y de altura 10 cm.
14. En un cono circular recto se inscriben
dos esferas tangentes exteriores cuyos
radios miden 3 y 5 . Halla la altura de
dicho cono.
7.
En un cono circular recto, el área de la
superficie lateral es el doble del área de
su base. Calcular el volumen del cono si
su altura mide 6.
15. Halla la relación entre los volúmenes de
un tronco de cono cuyas bases tienen
áreas iguales a 4 y 16, y la esfera
inscrita.
8.
Se tiene un cono recto de revolución. Se
traza un plano paralelo a la base por el
punto medio de la altura. ¿En qué
relación están los volúmenes del cono
total y el tronco de cono?.
14
PROGRAMA DE COMPLEMENTACION ACADEMICA
5TO DE SECUNDARIA
GEOMETRIA - GUIA Nº10
TEMA: ESFERA
BIMESTRE II
Una esfera es un cuerpo geométrico limitado
por una superficie curva cerrada cuyos
puntos equidistan de otro interior llamado
centro de la esfera.
VOLUMEN:
V=
h 2
3
3r  h
ZONA ESFERICA
Es la parte de la esfera cortada por 2 planos
paralelos
VOLUMEN :
AREA :
4
V  R 3
3
AREA LATERAL:
A = 4 R2
VOLUMEN:
CASQUETE ESFERICO
Un casquete esférico es la parte de una
esfera cortada por un plano.
V
AL = 2 R h
h
6
(h2  3R 2  3r 2 )
PROBLEMAS
13. Halla el volumen y el área total de una
semiesfera cuyo radio mide 10 m.
14. Halla el volumen de un cubo sabiendo
que el área de la esfera inscrita es 16.
15. Halla el volumen de la esfera circunscrita
a un cubo de arista L.
AREA:
16. Una semiesfera está inscrita en un
cilindro de radio R. Halla el volumen de
la parte interior al cilindro pero exterior a
la semiesfera.
A = 2 R h
15
longitud al diámetro de su base; la esfera
interna está inscrita en el mismo cono.
Determine el volumen del espacio entre las
dos esferas.
17. Se traza un plano secante a una esfera a
4m de su centro, determinando una
sección recta de área igual a 9. Halla el
radio de la esfera.
13. Cuatro esferas de radio igual a 10m son
tangentes entre sí formando una pila.
(una de ellas sobre las otras tres).
Calcula la altura de la pila. Halla el
volumen de un cono de 6m de altura
sabiendo que su base tiene un radio de
3m.
18. En un recipiente cilíndrico de diámetro 4
y que contiene agua hasta la mitad se
introduce una esfera de metal, y el nivel
del agua sube 3,5. Halla el volumen de la
esfera.
14. Se inscribe un cono en una esfera, tal
que la generatriz del cono sea igual al
diámetro de su base e igual a 2r. Calcula
el área de la esfera en función de r.
19. Cuatro esferas de radio 10m son
tangentes entre sí formando una pila. (
una de ellas sobre las potras tres).
Calcula la altura de la pila.
20. Halla el área de la esfera inscrita en un
cono equilátero de 81m2 de área total.
21. La relación entre los volúmenes de 2
esferas concéntricas es 8. halla la
relación entre las áreas de dichas
esferas.
9.
Una esfera está inscrita en un cono y la
longitud del diámetro de la base del cono
es igual a la longitud de la generatriz del
mismo, los cuales miden 10 cm.
Determina el volumen de la esfera.
15. Se tiene una esfera de centro O y radio
5. Un plano P corta a la esfera en una
circunferencia C y la distancia de O a P
es 4, Calcula el volumen del cono con
vértice O y como base el círculo limitado
por C.
10. Una esfera está situada dentro de un
cilindro de manera que la altura y el
diámetro del cilindro tienen la misma
dimensión que el diámetro de la esfera.
Determine la relación entre el área de la
superficie esférica y el área de la
superficie lateral del cilindro.
16. Un cono circular recto está inscrito en
una esfera cuya área es igual al área de
la base del cono. Un segundo cono tiene
el mismo vértice y su base es el círculo
limitado por los puntos de tangencia
entre el 1er cono y la esfera. Halla la
relación entre las áreas laterales del 2do
cono y el 1ro.
11. En una esfera de radio r se tiene inscrito
un cilindro de tal manera que el diámetro
del cilindro es congruente con el radio de
la esfera. Calcule la relación entre el
volumen del cilindro y el volumen de la
esfera.
12. Sean dos esferas concéntricas, con la
característica de que la esfera externa se
encuentra circunscrita a un cono cuya
generatriz mide 3 cm., y es igual en
16
Nombre
Dibujo
Desarrollo
Área
Volumen
Cubo o
Hexaedro
A = 6a2
V = a3
Paralelepípedo
u ortoedro
A = 2(ab+ac+bc)
V = abc
Prisma
AT = 2AB + AL
V = ABH
Cilindro
AT = AB + AL
Pirámide
Cono
Tronco de
pirámide
AT = AB1 + AB2 + AL
Tronco de
cono
V
esfera
17

h 2
R1  R 22  R1R 2
3

18