INICIACION DE ELECTRONICA DIGITAL

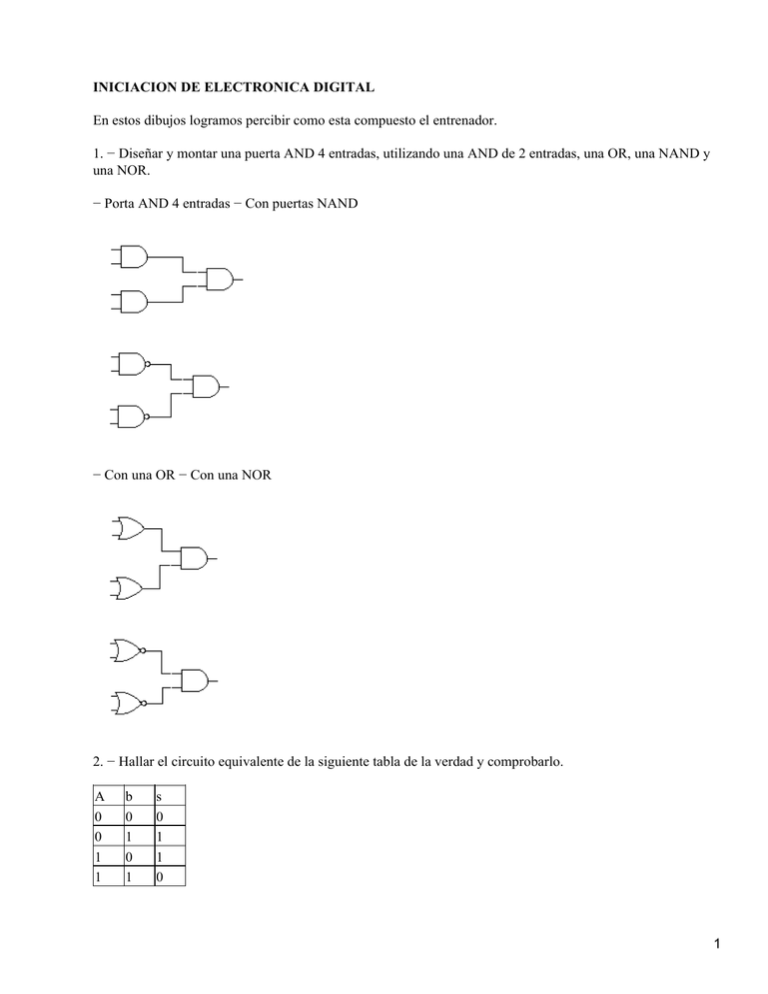
INICIACION DE ELECTRONICA DIGITAL
En estos dibujos logramos percibir como esta compuesto el entrenador.
1. − Diseñar y montar una puerta AND 4 entradas, utilizando una AND de 2 entradas, una OR, una NAND y
una NOR.
− Porta AND 4 entradas − Con puertas NAND
− Con una OR − Con una NOR
2. − Hallar el circuito equivalente de la siguiente tabla de la verdad y comprobarlo.
A
0
0
1
1
b
0
1
0
1
s
0
1
1
0
1
Esta tabla de la verdad es equivalente a la OR−EXCLUSIVE
3.− Hallar la función
S = (abc + d) +ef
4. − Atinar la función y montaje del circuito.
S = abc + (a + b + c) d
5. − Hacer el circuito a partir de la siguiente función.
F =(a + b) c · d
2
6. − Crear con puertas NAND el resto de las puertas.
3
7. − Montar los circuitos, hacer la tabla de la verdad.
a
a
b
b
s
s
0
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
0
0
1
1
1
1
0
0
4
Podemos observar en estos dos circuitos que funcionan como puertas NOR.
8. − Compruebe los siguientes postulados
a+a=a
a·a=a
a·1=1
a+0=a
a+a=1
a·a=0
a+1=1
a + ab = a
a · (a+b) = a
a=a
a=a
a + ab = a + b
a (a + b) = ab
a + b = ab
ab = a + b
a·0=0
9. − Tenemos una central de alarma que se disparará con la siguiente combinación de sectores activados.
• A y B activados; C y D en reposo
• A y D activados; B y C en reposo
• A, B y D activados; C en reposo
• A activado y el resto en reposo
• A, B y C activados; D en reposo
• A y C activados; B y D en reposo
Realizar la tabla de la verdad y montar el circuito con las puertas lógicas.
F = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD + ABCD
5
A
1
B
1
C
1
D
1
S
1
0
1
0
1
0
F = AC + AD + BCD
0
0
0
0
0
1
0
0
0
1
0
1
0
0
1
1
0
0
6
1
0
0
0
0
1
0
1
0
0
1
1
0
0
0
1
1
1
0
1
0
0
0
1
1
0
7
0
1
1
1
0
1
0
1
1
0
1
1
0
1
1
0
0
1
1
1
0
1
1
1
1
1
8
0
1
1
1
1
1
0
10. − Diseñar un circuito de 4 entradas para que a la salida de 1 solo con la combinación 1101 = 1.
F = DCBA
11. − Simplifica y monta la función.
F = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD
F = ABCD + ABCD + ABCD + ABCD + ABCD
1
9
1
1
1
1
F = ABC + ABC +ABC +ABC +ABC
1
1
1
1
1
F = C + AB
12. − Sacar la tabla de la verdad, la función y simplifícala.
A
0
0
0
0
0
0
0
0
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
C
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
S
0
0
0
1
0
1
0
1
0
1
0
1
10
1
1
1
1
1
1
1
1
0
0
1
1
0
1
0
1
0
1
1
1
F = AD + BD + CD + ABC
F = BD (A + A) (C + C) + AD (B + B) (C + C) + CD (A + A) (B + B) + ABC(D + D) = BDAC + BDAC +
BDAC+ BDAC + ADBC +ADBC + ADBC + ADBC + CDAB + CDAB + CDAB + CDAB + ABCD +
ABCD
13. − Sacar la tabla de la verdad y simplificar la función dada.
F = ABCD + ABCD + ABCD + ABCD + ABCD + ABCD + ABCD + ABCD
Para simplificar esta función utilizaremos el método de Karnaugh, como en los ejercicios anteriores.
1
1
1
1
1
1
1
1
F = CA + DA + BA + DCA
La tabla de la verdad es la misma que en el ejercicio anterior.
14. − Diseñar el circuito y la tabla de la verdad de las siguientes funciones y montar los circuitos.
11
Estas son las funciones de los circuitos creados:
F1 = (A + B) C + AD
F2 = C (A + BD) + A + C
F3 = AB + BC + CA + CD + A + B
A
0
0
0
0
0
0
0
0
B
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
F1
0
0
0
0
0
1
0
1
F2
0
1
0
1
0
1
0
1
F3
1
1
0
1
0
1
1
1
12
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
1
0
1
0
1
1
1
1
1
1
1
1
0
1
1
1
1
1
1
1
1
1
1
1
15. − Diseñar todas las puertas con puertas NOR
16 − ¿Cuál es la puerta resultante?
Circuito
Equivalencia
13
OR
NOR
NAND
AND
17. − Actividad complementaria.
En la figura siguiente se muestra el dibujo de un sistema de apertura de la puerta de un garaje. Para que la
puerta se pueda abrir es necesario que tanto a la entrada como a la salida, el coche se encuentre bien situado
sobre la plataforma para que se activen los pulsadores A o B, y además que el conductor introduzca una llave
en el registro correspondiente (A2 o B2. Si un coche quiere salir y otro quiere entrar al mismo tiempo, la
puerta no se abrirá y una lámpara de color naranja indicará al conductor del coche que desea entrar que se
retire para que pueda salir el que está dentro. Otra lámpara del mismo color, que se ilumina al mismo tiempo
que la de fuera, indicará al conductor del coche de dentro que debe esperar hasta que se retire el de fuera. Otra
lámpara de color rojo, situado al principio del túnel de salida (visible desde las plazas de aparcamiento),
indicará al conductor que quiere salir del garaje que modere su velocidad y espere porque un coche está situad
en la plataforma de entrada.
El coche que quiera entrar o que quiera salir debe permanecer en reposo hasta que la puerta se haya abierto
completamente. El cierre de la puerta se produce automáticamente transcurrido un tiempo.
Desarrollar un circuito de control para la apertura de la puerta arrastrada por el motor M y para las señales
luminosas LN y LR. Montar el diagrama lógico con puertas NAND de dos entradas y comprobar el
funcionamiento. (No hay que definir el sistema automático de cierre ni los dispositivos de seguridad.
A1 = plataforma exterior B1 = plataforma exterior
A2 = llave exterior B2 = llave interior
M = on, cuando A1 y A2 = on, o también cuando B1 y B2 = on.
M = off, cuando A1, A2, B1, B2 = on.
14
LN = on, cuando hay un coche dentro y otro fuera. También se ilumina cuando A1 y A2 o B1 y B2 = on.
LN = off, cuando A1 o/i A2 = off.
LR = on, cuando A1 o/i A2 = on.
A1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
A2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
B1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
B2
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
M
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
LN
0
0
0
0
0
1
1
1
0
1
1
1
0
1
1
1
LR
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
• Como en los ejercicios anteriores obtenemos la función simplificada con el método de Karnaugh.
• M = A1A2B1B2 + A1A2B1B2
• LN = A2B2 + A2B1 + A1B2 + A1B1
• LR = A1A2B1B2 + A1A2B1B2
• Cuando obtenemos las funciones las complementamos con puertas NAND:
• M = A1A2B1B2 · A1A2B1B2
• LN = A2B2A2B1A1B2A1B1
• LR = A1A2A2B1B2
Circuito con diversas puertas:
15
En la practica este circuito no se ha montado por él numero de puertas que hacia falta, pero se ha probado con
el Wb5 y funciona correctamente.
Circuito con puertas NAND:
16
17