PROBLEMAS SOBRE LEY DE COULOMB

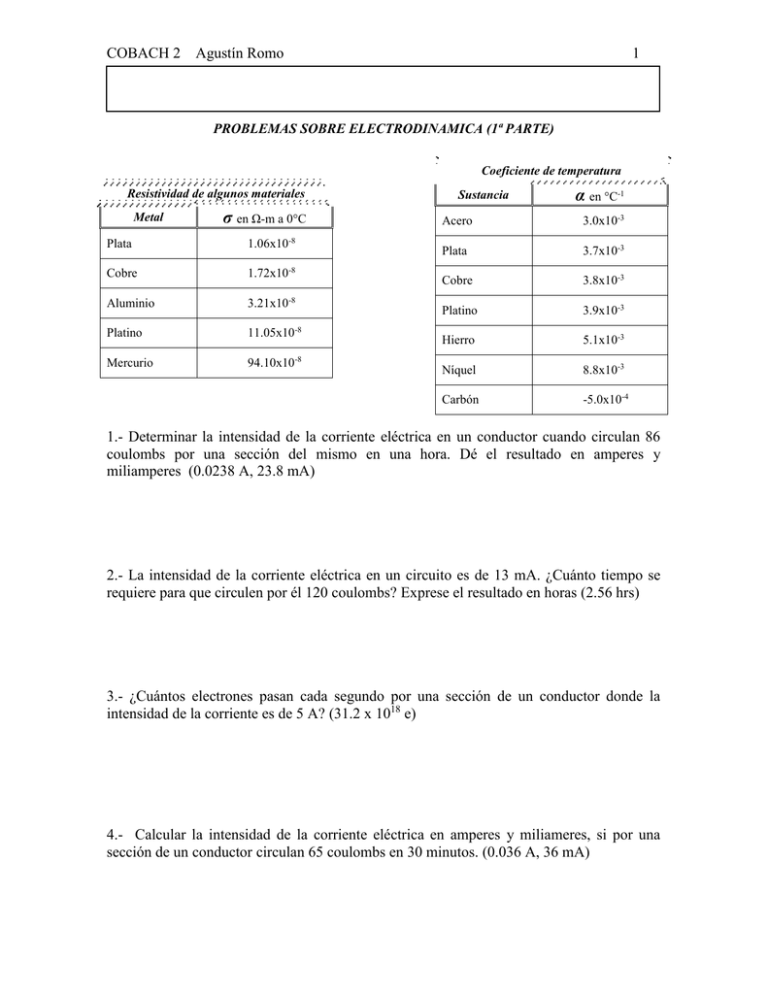
COBACH 2
Agustín Romo
1
PROBLEMAS SOBRE ELECTRODINAMICA (1ª PARTE)
Coeficiente de temperatura
Resistividad de algunos materiales
Metal
σ en Ω-m a 0°C
Plata
1.06x10-8
Cobre
1.72x10-8
Aluminio
3.21x10-8
Platino
11.05x10-8
Mercurio
94.10x10-8
Sustancia
α en °C-1
Acero
3.0x10-3
Plata
3.7x10-3
Cobre
3.8x10-3
Platino
3.9x10-3
Hierro
5.1x10-3
Níquel
8.8x10-3
Carbón
-5.0x10-4
1.- Determinar la intensidad de la corriente eléctrica en un conductor cuando circulan 86
coulombs por una sección del mismo en una hora. Dé el resultado en amperes y
miliamperes (0.0238 A, 23.8 mA)
2.- La intensidad de la corriente eléctrica en un circuito es de 13 mA. ¿Cuánto tiempo se
requiere para que circulen por él 120 coulombs? Exprese el resultado en horas (2.56 hrs)
3.- ¿Cuántos electrones pasan cada segundo por una sección de un conductor donde la
intensidad de la corriente es de 5 A? (31.2 x 1018 e)
4.- Calcular la intensidad de la corriente eléctrica en amperes y miliameres, si por una
sección de un conductor circulan 65 coulombs en 30 minutos. (0.036 A, 36 mA)
COBACH 2
Agustín Romo
2
5.- Determine la cantidad de electrones que pasan cada 10 segundos por una sección de un
conductor donde la intensidad de la corriente es de 20 mA (1.248 x 1018 e)
6.- Calcular el tiempo requerido para que por una sección de un conductor circulen 5
coulombs si la intensidad de la corriente es de 5 mA (1 x 103 seg)
7.- Determinar la resistencia eléctrica de un alambre de cobre de 2 km de longitud y
mm2 de área en su sección transversal a 0°C (43 Ω)
0.8
8.- La resistencia de un alambre de cobre es de 15 Ω a 0°C, calcular su resistencia a 60°C.
(18.42 Ω)
9.- Un termómetro de platino tiene una resistencia de 8 Ω a 150°C; calcular su resistencia a
400°C (12.93 Ω)
10.- Calcular la resistencia eléctrica a 0°C de un alambre de platino de 0.5 m de longitud y
0.7 mm2 de área en su sección transversal. (7.89 x 10-2 Ω)
COBACH 2
Agustín Romo
3
11.- Determine la longitud que debe tener un alambre de cobre enrollado de 0.5 mm2 de
área en su sección transversal para que a 0°C su resistencia sea de 12 Ω (349 m)
12.- Un alambre de plata tiene una resistencia de 5 Ω a 0°C ¿Cuál será su resistencia a
25°C? (5.46 Ω)
13.- Determinar la resistencia de un termómetro de platino a 500°C, si a 50°C su
resistencia es de 3.8 Ω (9.38 Ω)
14.-Determinar la intensidad de la corriente eléctrica a través de una resistencia de 30 Ω al
aplicarle una diferencia de potencial de 90 v (3 A)
15.- Un tostador eléctrico tiene una resistencia de 15 Ω ¿Cuál será la intensidad de la
corriente que fluirá al conectarlo a una línea de 120 v? (8 A)
COBACH 2
Agustín Romo
4
16.- Un alambre conductor deja pasar 6 A al aplicarle una diferencia de potencial de 110 V
¿Cuál será el valor de su resistencia? (18.33 Ω)
17.- Calcular la diferencia de potencial aplicada a una resistencia de 10 Ω si por ella fluyen
5 A. (50 V)
18.- Calcular la intensidad de la corriente que pasará por una resistencia de 20 Ω al
conectarse a un acumulador de 12 V (0.6 A)
19.- Determinar la resistencia del filamento de una lámpara que deja pasar 0.6 A de
intensidad al ser conectado a una diferencia de potencial de 120 V (200 Ω)
20.- Por una resistencia de 10 Ω circula una corriente de 2 A ¿Cuál es el valor de la
diferencia de potencial a que están conectados sus extremos? (20 V)
21.- Calcular la resistencia de un conductor que al conectarse a una diferencia de potencial
de 12 V deja pasar una corriente de 90 miliamperes. (133.33 Ω)
COBACH 2
Agustín Romo
5
22.- Calcular la resistencia equivalente de 3 resistencias cuyos valores son: R1 = 2 Ω ,
R2 = 5 Ω y R3 = 7 Ω conectadas en a) serie, b) paralelo [ a) 14 Ω, b) 1.19 Ω ]
23.- Calcule el valor de la resistencia que debe conectarse en paralelo con una resistencia
de 10 Ω para que la resistencia equivalente del circuito se reduzca a 6 Ω (15 Ω)
24.- Calcular la resistencia equivalente de 4 resistencias cuyos valores son: R1 = 10 Ω,
R2 = 20 Ω, R3 = 25 Ω y R4 = 50 Ω conectadas en a) serie b) paralelo. Dibujar el diagrama
para cada caso. [ a) 105 Ω, b) 4.76 Ω ]
COBACH 2
Agustín Romo
6
25.- Dos focos, uno de 70 Ω y otro de 80 Ω, se conectan en serie con una diferencia de
potencial de 120 V
a) Representar el circuito eléctrico
b) Calcular la intensidad de la corriente que circula por el circuito (0.8 A)
c) Determinar la caída de voltaje o de tensión en cada resistencia (56 V, 64 V)
26.- Una plancha eléctrica de 60 Ω se conecta en paralelo a un tostador de 90 Ω con un
voltaje de 120 V
a) Representar el circuito eléctrico
b) Determinar el valor de la resistencia equivalente del circuito (35 Ω)
c) Calcular la intensidad de la corriente que circula por el circuito (3.3 A)
d) ¿Qué valor tendrá la intensidad de la corriente que circula por cada resistencia? ( 2 A,
1.3 A)
COBACH 2
Agustín Romo
7
27.- Una serie formada por 9 focos de navidad con una resistencia de 20 Ω cada uno se
conecta a un voltaje de 120 v. Calcular:
a) ¿Cuál es el valor de la resistencia equivalente? (180 Ω)
b) ¿Cuál es la intensidad de la corriente que circula por cada resistencia? (0.67 A)
c) ¿Qué valor tendrá la caída de tensión en cada uno de los focos? ( 13.4 V)
28.- Tres aparatos eléctricos de 8 Ω, 15 Ω y 20 Ω, se conectan en paralelo a una batería de
60 V.
a) Representar el circuito eléctrico
b) Calcular el valor de la resistencia equivalente (4.15 Ω)
c) Determinar el valor de la corriente total suministrada por la batería (14.5 A)
d) ¿Cuál es el valor de la corriente que circula por cada aparato? (7.5 A, 4 A, 3 A)
COBACH 2
Agustín Romo
8
29.- En las siguientes figuras se muestran varios circuitos de conexiones mixtas de
resistencias. Calcular para cada caso:
a) La resistencia equivalente del circuito
b) La intensidad de la corriente total que circula por el mismo
a) 9.09 Ω
b) 4.4 A
a) 11.2 Ω
b) 1.78 A
COBACH 2
Agustín Romo
9
a) 44.26 Ω
b) 1.35 A
a) 5.3 Ω
b) 5.7 A
COBACH 2
Caso 5
Caso 6
Agustín Romo
10
a) 117 Ω
b) 0.13 A
a) 15.8 Ω
b) 0.76 A
COBACH 2
Caso 7
a) 22.5 Ω
b) 0.8 A
Caso 8
a) 10.87 Ω
b) 1.38 A
Agustín Romo
11
COBACH 2
Agustín Romo
12
30.- Si una batería tiene una fuerza electromotriz (fem) de 20 v, una resistencia interna de
1.5 Ω y se conecta a dos resistencias en serie cuyos valores son 8 y 15 Ω como se observa
en la figura, calcular:
a) La resistencia total del circuito (24.5 Ω)
b) La intensidad de la corriente que circula por el circuito (0.816 A)
c) La caída de tensión en cada una de las resistencias (6.6 V, 12.2 V, Vpila = 1.2 V)
d) El voltaje real que suministra la batería cuando está cerrado el circuito (18.8 V)
31.- Determinar el valor de la resistencia equivalente de dos resistencias cuyos valores son:
15 Ω y 23 Ω conectadas primero en serie y luego en paralelo. [ s) 38 Ω, p) 9.1 Ω]
32.- Calcular el valor de la resistencia equivalente de tres resistencias cuyos valores son:
17 Ω, 12 Ω y 25 Ω conectadas primero en serie y luego en paralelo. [ s) 54 Ω, p) 5.5 Ω]
33.- Calcular el valor de la resistencia que al ser conectada en paralelo con otra de 28 Ω
reduce la resistencia de un circuito a 8 Ω (11.2 Ω)
COBACH 2
Agustín Romo
13
34.- Determinar la resistencia equivalente de 4 resistencias cuyos valores son: 3 Ω, 1 Ω,
4 Ω y 2 Ω conectadas primero en serie y luego en paralelo. [ s) 10 Ω, p) 0.5 Ω]
35.- Tres focos de 40 Ω, 50 Ω y 60 Ω se conectan en serie a una batería de 90 v, calcular:
a) La intensidad de la corriente que circula por el circuito (0.6 A)
b) La caía de tensión en cada resistencia. ( 24 V, 30 V, 36 V )
36.- De acuerdo con el circuito eléctrico representado en la siguiente figura, calcular:
a) La resistencia equivalente del circuito (11 Ω)
b) La intensidad total de la corriente que circula por el circuito (1.8 A)
c) El valor de la intensidad de la corriente que circula por cada resistencia (0.66 A, 0.33 A,
0.8 A)
COBACH 2
Agustín Romo
14
37.- Siete focos de navidad con una resistencia de 30 Ω cada uno, se conectan en serie con
una diferencia de potencial de 90 v. Calcular:
a) La resistencia equivalente del circuito (210 Ω)
b) La intensidad de la corriente que circula por cada resistencia (0.43 A)
c) La caída de tensión en cada uno de los focos (12.9 V)
38.- Dibujar un circuito que represente tres resistencias de 19 Ω, 25 Ω y 30 Ω
respectivamente, conectadas en paralelo a una batería de 40 Ω, calcular:
a) La resistencia equivalente del circuito (7.9 Ω)
b) La intensidad de corriente suministrada por la batería (5.06 A)
c) El amperaje que circula por cada resistencia (2.1 A, 1.6 A, 1.3 A)
39.- Si una batería con una fem de 12 V y una resistencia interna de 1 Ω, se conecta a dos
resistencias en serie de 5 y 10 Ω respectivamente como se observa en la figura. Calcular:
a) La resistencia total del circuito (16 Ω)
b) La intensidad de corriente que circula por el circuito (0.75 A)
c) La caída de tensión en cada una de las resistencias (3.75 V, 7.5 V, Vpila = 0.75 V)
d) El voltaje real que suministra la batería cuando está cerrado el circuito (11.25 V)