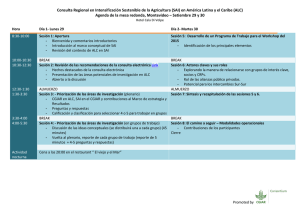
Tema 7 “ ” Lógicas de descripciones

Tema 7
“Lógicas de descripciones”
Año académico 2014/15
Profesores:
Sascha Ossowski, Alberto Fernández y Holger Billhardt
–1–
Referencias
•  Reasoning in Description Logics: Basics, Extensions, and
Relatives.
Ulrike Sattler. Reasoning Web 2007, LNCS 4636
•  Basic Description Logics.
Franz Baader, Werner Nutt. Cap. 2 en “The Description Logic
Handbook: Theory, Implementation, and Applications”. Cambridge
University Press, 2003.
•  Semantic Web: Concepts, Technologies and Applications.
K. Breitman, M. A. Casanova, W. Truszkowski. Springer. 2007
(Cap. 3)
•  Foundations of Semantic Web Technologies.
P. Hitzler, M. Krötzsch, S. Rudolph. CRC Press. 2009. (Cap. 5)
–2–
Índice
•  Representación del conocimiento
–  Sintaxis y semántica ALC
–  Bases de conocimientos
•  Inferencia
–  Mecanismos básicos
–  Otros mecanismos
•  ALC como Lógica de primer orden
–3–
Índice
•  Representación del conocimiento
–  Sintaxis y semántica ALC
–  Bases de conocimientos
•  Inferencia
–  Mecanismos básicos
–  Otros mecanismos
•  ALC como Lógica de primer orden
–4–
Introducción
•  Familia de formalismos de representación del conocimiento
basados en lógica
–  Describe el dominio en términos de:
•  Conceptos (clases): curso, profesor, universidad, …
•  Roles (relaciones): imparte-curso, asiste-a-curso, …
•  Individuos: Luis, Ana, Alberto, …
•  Los lenguajes particulares se caracterizan por:
–  El conjunto de constructores disponibles para construir conceptos y
roles complejos a partir de otros más simples
–  El conjunto de axiomas para añadir hechos sobre conceptos, roles
e individuos
•  Base lógica de OWL (Web Ontology Language)
–5–
Una lógica descriptiva (DL) básica: ALC
ALC (Attributive Language with Complements)
Sintaxis: descripción de conceptos ALC
Sea C un conjunto de nombres de conceptos y R un conjunto de nombres
de roles (relaciones o propiedades) disjunto de C
–  Cada nombre de concepto es concepto ALC
–  > y ? son conceptos ALC
–  Si C y D son conceptos ALC y r es un nombre de rol, entonces también
son conceptos ALC:
•  C u D (conjunción)
•  C t D (disyunción)
•  ¬C (negación)
•  9r.C (restricción existencial)
•  8r.C (restricción de valores)
–  Se usan paréntesis para clarificar la estructura de los conceptos
•  Orden precedencia de operadores como en lógica de primer orden
–6–
Una lógica descriptiva básica: ALC
Ejemplos
(asumiendo nombres de conceptos empiezan por mayúscula, nombres
de roles empiezan por minúscula)
–  Bien formados
• 
• 
• 
• 
• 
Persona u Femenino
Persona u 9asiste.Curso
A u 9r.8s.(E u ¬F)
Persona u 9imparte.(Curso u 8matriculado-por.(Inteligente u ¬Vago))
Hombre u ∃tieneHijo.Femenino u ∃tieneHijo.Masculino u ∀tieneHijo.
(Rico t Feliz)
–  Mal formados
•  8s.s
•  Persona ¬ Femenino
•  Persona u 9Curso
–7–
ALC: Semántica
• 
Interpretación I = (4I,·I)
–  4I es un conjunto no vacío (llamado dominio)
–  ·I es una función que asocia
• 
• 
Cada nombre de concepto A ∈ C a un conjunto AI ⊆ 4I
Cada nombre de rol r ∈ R a una relación binaria rI ⊆ 4I x 4I
·I se extiende a conceptos complejos de la siguiente manera:
>I = 4I
?I = ∅
(C u D)I = CI \Å DI
(C t D)I = CI [ DI
(¬C)I = 4I \ CI
(9r.C)I = {d ∈ 4I | ∃e ∈4I con <d,e>∈rI y e ∈CI }
(8r.C)I = {d ∈ 4I | 8e ∈4I , si <d,e>∈rI entonces e∈CI }
–8–
ALC: Ejemplo 1
• 
Interpretación I:
– 
– 
– 
– 
– 
– 
• 
trabajaPara
4I = {a, b, c, d}
a
EmpleadoI = {a}
trabajaPara
PersonaI = {a, b}
EmpresaI ={c, d, b}
c
I
SociedadAnónima = {d}
trabajaParaI = {<a,c>, <a,d>, <b,b>}
d
b
trabajaPara
Algunas observaciones sobre I:
– 
– 
– 
– 
– 
– 
– 
– 
Todos los elementos son instancia de > y ninguno es de ?
a es una instancia de Persona u Empleado
c es una instancia de Empresa u ¬Persona
a y b son instancias de 9trabajaPara.Empresa, pero sólo a es instancia
de 9trabajaPara.¬Persona
Todos los elementos son instancia de 8trabajaPara.Empresa
a no es instancia de 8trabajaPara.(Empresa u SociedadAnónima)
c y d son instancias de 8trabajaPara.?
…
–9–
Bases de Conocimientos ALC
•  Normalmente, una BC se divide en dos partes <T,A>:
–  Tbox (Terminological KB): un conjunto de axiomas que describen la
estructura de un dominio, de la forma:
•  Inclusiones: C v D, siendo C y D conceptos ALC
C v D sii CI µ DI
•  Equivalencias: C ≡ D (si C es atómico se llama Definición)
C ≡ D sii C v D y D v C (es decir, CI ≡ DI)
•  I es un modelo de T si y sólo si satisface todos los axiomas de T
–  Abox (Assertional KB): un conjunto de axiomas que describen una
situación concreta, de la forma:
•  Aserción de conceptos: C(a)
C(a) si aI ∈CI
•  Aserción de roles: r(a,b)
r(a,b) si <a,b>∈rI
– 10 –
Bases de Conocimientos: Ejemplo 2
T = { Empresa v ¬Persona,
TBox
EmpresaPrivada v Empresa,
Empleado ≡ Persona u 9trabajaPara.Empresa
SociedadAnónima v Empresa,
Empleado v Persona u 9trabajaPara.Empresa,
Persona u 9trabajaPara.Empresa v Empleado,
9trabajaPara.> v Persona,
Empresario v Persona u 9posee.Empresa,
Persona u 9posee.Empresa v Empresario,
9posee.> v Persona }
Empresario ≡ Persona u 9posee.Empresa
– 11 –
Bases de Conocimientos: Ejemplo 2 K=<T,A>
T = { Empresa v ¬Persona,
EmpresaPrivada v Empresa,
SociedadAnónima v Empresa,
Empleado ≡ Persona u 9trabajaPara.Empresa,
9trabajaPara.> v Persona,
Empresario ≡ Persona u 9posee.Empresa,
9posee.> v Persona }
A = {Persona(Ana),
Empresa (IBM),
(Empresa u SociedadAnónima)(Telefónica),
Persona(Luis)
(Persona u Empleado)(Marta),
trabajaPara(Ana,IBM),
trabajaPara(Luis,Telefónica),
posee(Marta,Telefónica),
posee(Ana,Telefónica)}
TBox
ABox
– 12 –
Índice
•  Representación del conocimiento
–  Sintaxis y semántica ALC
–  Bases de conocimientos
•  Inferencia
–  Mecanismos básicos
–  Otros mecanismos
•  ALC como Lógica de primer orden
– 13 –
Inferencia
•  Mecanismos básicos de razonamiento: dada una BC K=<T,A>,
los conceptos C y D, y un individuo a:
–  Satisfacibilidad: C es satisfacible
•  sii existe un modelo I de T y un b ∈4I con bI ∈CI (CI ≠ ∅)
–  Subsunción: C es subsumido por D (C vT D o T ╞ C v D)
•  sii CI µ DI para cada modelo I de T
–  Equivalencia: C y D son equivalentes (C ≡ T D)
•  sii CI ≡ DI para cada modelo I de T
–  Disjunto: C y D son disjuntos (C uT D ≡ ? o C vT ¬D)
•  sii para cada modelo I de T CI \Å DI = ∅
–  Consistencia: K es consistente
•  sii existe algún modelo de K
–  Instancia: a es una instancia de C
•  sii aI ∈ CI para cada modelo I de T
– 14 –
Inferencia
•  Propiedades de relación de subsunción
Sean C, D, y E conceptos, a un nombre de individuo, y <T,A> una BC
–  C vT C (reflexiva)
–  Si C vT D y D vT E, entonces C vT E (transitiva)
–  Si a es una instancia de C y C vT D, entonces a es una instancia
de D
– 15 –
Inferencia
•  Ejemplos:
– 
– 
– 
– 
A u ¬A es insatisfacible
? y A u ¬A son equivalentes
9r.A u 8r.¬A es insatisfacible
A u B es subsumido por A (A u B vT A)
•  Del ejemplo 2 se deduce, entre otras cosas:
– 
– 
– 
– 
SociedadAnónima vT ¬Persona
9trabajaPara.Empresa vT ¬Empresa
Ana y Luis son instancias de Empleado
Empresa u 9trabajaPara.Empresa es insatisfacible
– 16 –
Inferencia
•  Otros mecanismos de razonamiento más sofisticados
–  Clasificación de una TBox T
•  Computar la jerarquía de subsunción entre todos los nombres de
conceptos en T. Es decir, para cada par de conceptos C, D comprobar si
C es subsumido por D y si D es subsumido por C
–  Comprobar la satisfacibilidad de conceptos en T.
•  Para cada concepto C en T , comprobar si C es satisfacible (de lo
contrario hay un error de modelado)
–  Recuperación de instancias
•  Dado un concepto C y una base de conocimiento K, devolver todos los
nombres de individuos a que sean instancia de C.
–  Realización de un nombre de individuo
•  Dado un individuo a y una base de conocimiento K, comprobar, para cada
nombre de concepto C de T , si a es instancia de C, y devolver todos los
C que a es instancia
– 17 –
Índice
•  Representación del conocimiento
–  Sintaxis y semántica ALC
–  Bases de conocimientos
•  Inferencia
–  Mecanismos básicos
–  Otros mecanismos
•  ALC como Lógica de primer orden
– 18 –
ALC como Lógica de primer orden
•  Se interpreta:
–  Nombres de conceptos ⇔ Predicados unarios
–  Nombres de roles ⇔ Predicados binarios
–  Conceptos ⇔ Fórmulas con una variable libre
•  Definición de conceptos ALC:
– 
– 
– 
– 
– 
– 
πx(A) = A(x)
(πx(>) = Cierto, πx(?) = Falso)
πx(¬C) = ¬πx(C)
πx(C u D) = πx(C) ^Æ πx(D)
πx(C t D) = πx(C) _Ç πx(D)
πx(9r.C) = 9y(r(x,y) ^Æ πy(C))
πx(8r.C) = 8y(r(x,y) ! πy(C))
– 19 –
ALC como Lógica de primer orden
•  TBoxes
–  π(T ) =
^Æ
C v D 2T
8x(πx(C) ! πx(D))
•  ABoxes
–  Nombres de individuos a ⇔ constantes
–  Sea ψ[x/a] la fórmula obtenida al reemplazar en ψ todas las
apariciones libres de x por a.
–  π(A ) =
^Æ
C(a) 2A
πx(C)[x/a] ^Æ
^Æ
r(a,b)2A
r(a,b)
– 20 –