quimica - Servidor de Apoyo al Sistema Escolarizado -

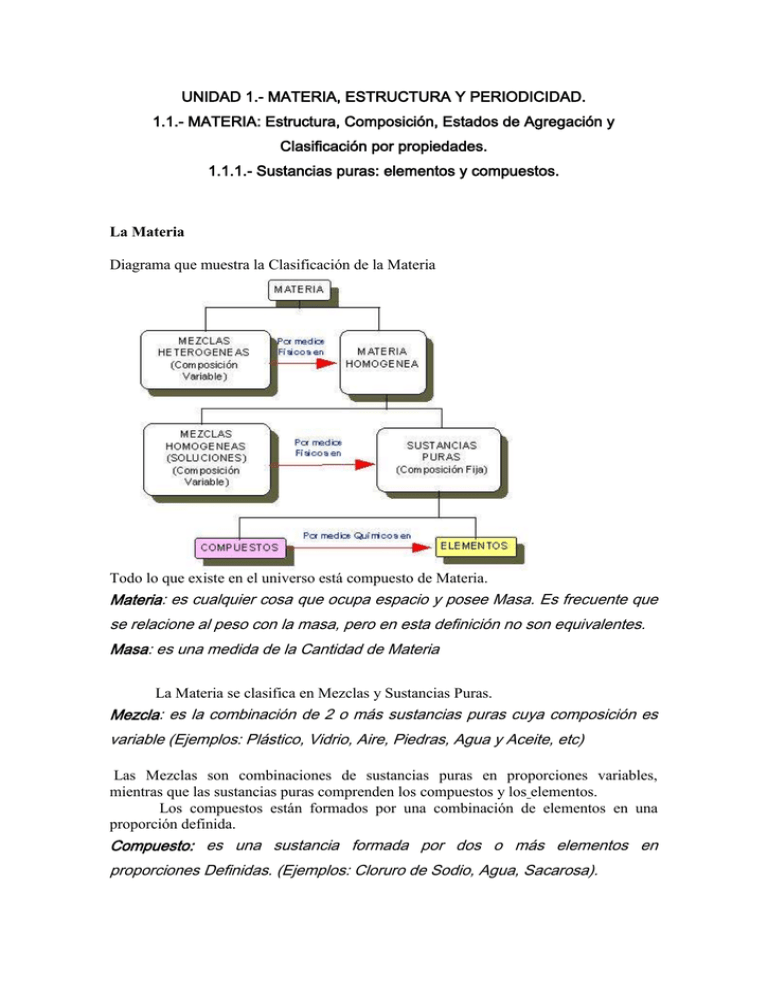
UNIDAD 1.- MATERIA, ESTRUCTURA Y PERIODICIDAD.
1.1.- MATERIA: Estructura, Composición, Estados de Agregación y
Clasificación por propiedades.
1.1.1.- Sustancias puras: elementos y compuestos.
La Materia
Diagrama que muestra la Clasificación de la Materia
Todo lo que existe en el universo está compuesto de Materia.
Materia: es cualquier cosa que ocupa espacio y posee Masa. Es frecuente que
se relacione al peso con la masa, pero en esta definición no son equivalentes.
Masa: es una medida de la Cantidad de Materia
La Materia se clasifica en Mezclas y Sustancias Puras.
Mezcla: es la combinación de 2 o más sustancias puras cuya composición es
variable (Ejemplos: Plástico, Vidrio, Aire, Piedras, Agua y Aceite, etc)
Las Mezclas son combinaciones de sustancias puras en proporciones variables,
mientras que las sustancias puras comprenden los compuestos y los elementos.
Los compuestos están formados por una combinación de elementos en una
proporción definida.
Compuesto: es una sustancia formada por dos o más elementos en
proporciones Definidas. (Ejemplos: Cloruro de Sodio, Agua, Sacarosa).
Elemento: es una sustancia que no puede descomponerse en otras más
simples. (Ejemplos: Oxígeno, Nitrógeno, Carbón)
Si se hace reaccionar Sodio (Na) con Cloro (Cl2) se obtendrá Na1Cl1
exclusivamente y no sustancias tales como Na0.5Cl2.3 o mezclas raras.
Las Mezclas se clasifican en Mezclas Homogéneas (Soluciones) y Mezclas
Heterogéneas. En una Mezcla Heterogénea pueden distinguirse con facilidad las
diferentes fases que forman la Mezcla, mientras que en una Mezcla Homogénea no hay
distinción de fases.
Mezcla Homogénea: es una mezcla uniforme en su Totalidad y suele llamarse
solución (Ejemplo: Aire, Sal en Agua). Las Aleaciones (Mezcla de Metales) son
soluciones sólidas.
Mezcla Heterogénea: es una mezcla no uniforme y consiste de partes que son
físicamente distintas (Piedras en Agua, Agua y Aceite, etc).
Fase: es una porción físicamente distinta de Materia que es Uniforme en su
Composición y Propiedades. (Podemos decir que una fase la constituye una
porción de sustancia pura).
Las Mezclas se separan en sus componentes por procesos físicos, mientras que los
Compuestos se separan en sus constituyentes por procesos químicos.
CLASIFICACIÓN DE LAS SUSTANCIAS PURAS:
SUSTANCI
AS PURAS
SUSTANCIA
S SIMPLES
Aquellas que no se pueden
descomponer químicamente en otras;
sus moléculas estan formadas por
átomos iguales. Ejemplos: Oxígeno,
Cloro; Sodio; Hierro.
SUSTANCIA
S
COMPUEST
AS
Se
pueden
descomponer
químicamente en otras; sus moléculas
están formadas por átomos diferentes.
Son también llamados Compuestos.
Ejemplos:
agua,
Anhídrido
Carbónico, Ácido Sulfúrico.
Propiedades de la Materia
Hay dos tipos de propiedades que presentan la Materia, Propiedades Extensivas y
Propiedades Intensivas. Las Propiedades Extensivas dependen de la cantidad de
Materia, por ejemplo, el peso, volumen, longitud, energía potencial, calor, etc. Las
Propiedades Intensivas no dependen de la Cantidad de Materia y pueden ser una
relación de propiedades, por ejemplo: Temperatura, Punto de Fusión, Punto de
Ebullición, Indice de Refracción, Calor Específico, Densidad, Concentración, etc.
Propiedades Extensivas: Propiedades que dependen de la Cantidad de
Sustancia (Por ejemplo: Calor, Energía, Peso, Volumen, Longitud, Area)
Propiedades Intensivas: Propiedades que no dependen de la Cantidad de la
Sustancia (Por ejemplo: Densidad, Punto de Fusión, Indice de Refracción,
Punto de Ebullición, Temperatura).
Punto de Fusión: Temperatura a la cual la Fase Sólida se encuentra en
equilibrio con la Fase Líquida
Punto de Ebullición: Temperatura a la cual la Presión de Vapor que escapa del
Líquido es igual a la Presión Exterior.
Presión de Vapor: Presión del Vapor que emana de un líquido al establecerse
el equilibrio (Velocidad de Evaporación = Velocidad de Condensación) a una
temperatura dada.
Las Propiedades Intensivas pueden servir para identificar y caracterizar una sustancia
pura. A continuación se presenta una tabla con algunas de estas propiedades para el
Agua.
Tabla: Propiedades físicas del Agua
Propiedad
Punto de Fusión a 1 atmósfera de Presión
Valor
100 °C
Punto de Ebullición a 1 atmósfera de Presión
0 °C
Densidad a 0 °C (hielo)
0.9168 g/mL
Densidad a 0 °C (agua líquida)
0.9998 g/mL
Densidad a 4 °C
1.0000 g/mL
Densidad a 20 °C
0.99823 g/mL
Punto Triple (a 4.58 mm de Hg de presión)
0.0075 °C
Calor Específico del hielo
0.487 cal/g °C
Calor Específico del Agua
1.000 cal/g °C
Calor Específico del Vapor (a 1 atmósfera de presión) 0.462 cal/g °C
Calor de Fusión (0 °C)
79.67 cal/g
Calor de Vaporización (o Evaporación)
539.55 cal/g
Indice de Refracción a 20 °C
1.3333
Temperatura Crítica
374.2 °C
Presión Crítica
218.5 atmósferas
Ejercicio: Clasifique los siguientes Materiales en las siguientes categorías: Mezcla
Heterogénea, Mezcla Homogénea, Compuesto, Elemento.








Cerveza
Mercurio
Madera
Acero
Escombro
Acido Acético
Oxido de Zinc
Plomo
1.1.2.- Dispersiones o Mezclas.
CLASIFICACIÓN DE LOS SISTEMAS DISPERSOS O MEZCLAS:
Según el tamaño de las partículas dispersas, los sistemas dispersos se clasifican en
dispersiones y soluciones.
 = micrón (milésima parte de un centímetro) 1 = 10-6 m.
p = partícula.
Dispersiones Macroscópicas
o Groseras o Gruesas Ej:
Azufre y Limadura de
Hierro
Sistemas
Dispersos
(Mezclas)
Sistemas
Heterogéneos
“Dispersiones”
EMULSIONES Ej: Leche
(líquido en líquido)
Dispersiones
(50>p>0,1)
Finas
SUSPENSIONES
Ej:
Carbón en H2O (sólido en
líquido)
Dispersiones
Coloidales
(0,1>p>0,001) Ej: Clara
de huevo en H2O
Sistemas
Homogéneos
“Soluciones”
Soluciones VERDADERAS
(p<0,001) Ej: Solución de
Sal en H2O
Según el estado de agregación de las fases Dispersas y Dispersantes, las dispersiones
se clasifican en:
Gas (aire)
GAS en
Líquido (soda)
Sólido (esponja)
Gas (niebla)
Dispersiones
de partículas
de
LÍQUIDO
en
Líquido (alcohol en agua)
Sólido (azúcar húmedo)
Gas (humo)
SOLIDO
en
Líquido (agua y sal)
Sólido (azufre y limaduras de
hierro)
DISPERSIONES COLOIDALES
El tamaño de las partículas oscila entre 0,1 y 0,001. A las partículas dispersadas en
un sistema coloidal se las denomina micelas. Cuando las micelas se hallan dispersas en
cantidad suficiente de líquido, el Coloide se denomina Sol.
Si el dispersante es agua -------------> Hidrosol
Si el dispersante es alcohol ----------> Alcohosol
Las partículas coloidales no se depositan, a pesar de ser más densas que el medio
dispersante. Esto se debe a que tales partículas están animadas en un movimiento
desordenado y constante que es el movimiento Browniano, que proviene del bombardeo
que experimentan las partículas coloidales por parte de las moléculas de la fase
dispersante externa.
PREPARACIÓN DE DISPERSIONES COLOIDALES:
Se obtienen por dos métodos generales:
a)
Por dispersión.
b)
Por condensación.
a)
El método de dispersión consiste en disminuir el tamaño de las partículas de la
fase interna en otras de menor tamaño, hasta alcanzar valores de 0,1>p>0,001.
b)
En cambio los métodos de condensación consisten en hacer que los iones o
moléculas de una solución se reúnan formando partículas de mayor diámetro, para
llegar a los valores de 0,1>p>0,001.
SEPARACIÓN DE LOS COMPONENTES DE UNA MEZCLA:
Se pueden separar por métodos mecánicos, físicos o por combinación de ambos.
Solubilización
Tamización
Sólido
Levigación y Almagamación
Flotación
Filtración
SÓLID
O EN
Líquid
o
Decantación
Centrifugación
Evaporación
Filtración
Gas
Por campo electrostático
(Proceso Cottrell)
SEPARACIÓ
N DE
No miscibles
Decantaci
ón
Destilació
n Simple
LÍQUI
DO EN
Destilació
n
Fracciona
da
Líquid
o
Miscibles
Destilació
n
en
corriente
de vapor
de H2O
Destilació
n al vacío
GAS
EN
Gas
Filtración
Sólido
Calentamiento
Líquid
o
Calentamiento
Gas
Licuación
y
Fraccionamiento
posterior
Levigar: Diluir en agua una materia en polvo para separar la parte mas fina.
FRACCIONAMIENTO DE FASES:
Los siguientes métodos se aplican para la separación se fases en sistemas
Homogéneos.
a)
b)
Cristalización.
Destilación: Simple – Fraccionada – Al vacío o presión reducida – En corriente de
vapor.
c)
Extracción por Distribución o reparto.
d)
Fusión Zonal o fusión por zonas.
e)
Cromatografía: En papel – En placa fina – En fase vapor o gaseosa – Líquido
líquido - En columna.
SOLUCIONES Y SUSTANCIAS PURAS:
Los sistemas Homogéneos se clasifican en:
Sustancias Puras: (Ej.: Agua)
Soluciones (Ej.: Agua y Sal)
Son Sustancias Puras o especies químicas aquellas en que las propiedades intensivas se
mantienen constantes resistiendo los procesos de fraccionamiento.
Son Soluciones los sistemas homogéneos que pueden fraccionarse en componentes más
sencillos por medios físicos. Dichos componentes son a su vez sustancias puras.
Tienen composición definida
SUSTANCI
AS PURAS
No se fraccionan
Ejemplos: Alcohol, Azúcar, Agua
No tienen proporciones definidas
SISTEMA
HOMOGÉNE
O
SOLUCION
ES
Se
fraccionan,
sustancias puras
obteniéndose
Ejemplos: Azúcar en agua [sólidolíquido]; Alcohol en agua [líquidolíquido]; Dióxido de Carbono en agua
[gas-líquido]
1.1.3.- Caracterización de los Estados de Agregación: sólido cristalino, líquido,
sólido, vítreo y gel.
Introducción.
Los diferentes estados en que podemos encontrar la materia de este
universo en el que vivimos se denominan estados de agregación de la
materia, porque son las distintas maneras en que la materia se
"agrega", distintas presentaciones de un conjunto de átomos. Los
estados de la materia son cinco:
1.
2.
3.
4.
5.
Sólido
Líquido
Gaseoso
Plasma
Condensado de Bose-Einstein
Los tres primeros son de sobra conocidos por todos nosotros y los
encontramos en numerosas experiencia de nuestro día a día. El
sólido lo experimentamos en los objetos que utilizamos, el líquido
en el agua que bebemos y el gas en el aire que respiramos.
El plasma es un estado que nos rodea, aunque lo experimentamos
de forma indirecta. El plasma es un gas ionizado, esto quiere decir
que es una especie de gas donde los átomos o moléculas que lo
componen han perdido parte de sus electrones o todos ellos. Así, el
plasma es un estado parecido al gas, pero compuesto por electrones,
cationes (iones con carga positiva) y neutrones. En muchos casos, el
estado de plasma se genera por combustión.
El Sol situado en el centro de nuestro sistema solar está en estado de
plasma, no es sólido, y los conocidos tubos fluorescentes contienen
plasma en su interior (vapor de mercurio). Las luces de neón y las
luces urbanas usan un principio similar. La ionosfera, que rodea la
tierra a 70,80 km de la superficie terrestre, se encuentra también en
estado de plasma. El viento solar, responsable de las deliciosas
auroras boreales, es un plasma también.
En realidad, el 99% de la material conocida del universo se encuentra
en estado de plasma. Aunque también es verdad que sólo conocemos
el 10% de la material que compone el universo. Esto significa que el
escaso 105 de materia que hemos estudiado, el 99% es plasma, o
sea, casi todo es plasma en el universo.
Es interesante analizar que los griegos sostenían que el universo
estaba formado por cuatro elementos: aire, agua, tierra y fuego.
Haciendo un símil, podríamos asignar un elemento físico a cada
elemento filosófico:
Aire - Gas
Agua - Líquido
Tierra - Sólido
Fuego - Plasma
¿Dónde podemos incluir el condensado de Bose - Einstein?
Condensado de Bose - Einstein
En 1920, Santyendra Nath Bose desarrolló una estadística mediante
la cual se estudiaba cuándo dos fotones debían ser considerados
como iguales o diferentes. Envió sus estudios a Albert Einstein, con el
fin de que le apoyara a publicar su novedoso estudio en la comunidad
científica y, además de apoyarle, Einstein aplicó lo desarrollado por
Bose a los átomos. Predijeron en conjunto el quinto estado de la
materia en 1924.
No todos los átomos siguen las reglas de la estadística de BoseEinstein. Sin embargo, los que lo hacen, a muy bajas temperaturas,
se encuentran todos en el mismo nivel de energía.
Explicación Intutiva
Es difícil entender intuitivamente qué significa el Condensado de
Bose-Einstein (CBE). En el CBE, todos los átomos se encuentran en el
mismo lugar, aunque esto va en contra de todo lo que vemos a
nuestro alrededor.
A las temperaturas increíblemente bajas que se necesitan para
alcanzar el estado de condensado de Bose-Einstein, se observa que
los átomos pierden su identidad individual y se juntan en una masa
común que algunos denominan superátomo.
Figura 1
El la figura 1 hemos considerado una visión intuitiva de la estructura
de un átomo representando el núcleo (formado por protones y
neutrones) por una bolita maciza roja, y la corteza de electrones que
lo rodean por una bola hueca roja también. La bola con un punto en
el centro constituye un átomo completo eléctricamente neutro.
Estado Sólido: podemos ver que los átomos se hallan dispuestos en
un volumen pequeño, se sitúan adyacentes, uno al lado del otro,
aunque no en contacto, formando generalmente una estructura.
Estado Líquido: los átomos se encuentran esparcidos en un
volumen mayor, sin seguir ninguna estructura. La separación entre
cada átomo es mayor que en el sólido.
Estado Gaseoso: los átomos ocupan un volumen mucho mayor. Es
el estado en que los átomos están más separados.
Estado de Plasma: sus componentes no son átomos, sino partículas
individuales y núcleos de átomos. Parece un gas, pero formado por
iones (cationes -núcleos y protones con carga positiva-, neutrones sin
carga y electrones -con carga negativa-). Cada componente del
estado de plasma está cargada eléctricamente y el conjunto ocupa un
gran volumen.
Condensado de Bose-Einstein: todos los átomos se encuentran en un
mismo lugar. En la figura 1, la única bola roja representa la posición
donde se hayan todos lo átomos, pero no uno sobre otro, sino todos
ocupando el mismo espacio físico.
Para hacernos una idea de lo que sería un objeto cotidiano estando
en estado de Bose-Einstein, proponemos imaginar que varias
personas estuvieran sentadas en la misma silla, no una sentada sobre
otra, sino literalmente todas sentadas en la misma silla, ocupando el
mismo
espacio
en
el
mismo
momento.
Explicación a través del concepto de ondas
Una explicación de cómo se forma el CBE es teniendo en cuenta que
la temperatura de un sistema es una medida del movimiento de sus
átomos.
Los átomos, como todas las partículas, son también ondas (dualidad
onda-corpúsculo). Están moviéndose continuamente, y cuanto más
lento se mueven, su longitud de onda es más larga.
Figura 5
En la figura 5 se muestran dos casos. En el primero (el de la
izquierda) se encuentra un sistema con átomos en diferentes estados
vibratorios, es decir, con diferentes energías. Por eso tienen distintas
ondas asociadas a diferentes velocidades. La cubeta de abajo
representa el sistema, las franjas horizontales representan los
diferentes estados energéticos y los puntos son los átomos situados
en estos distintos estados.
El segundo sistema (el de la derecha) representa un conjunto de
átomos que han sido enfriados hasta llegar a formar un condensado
de Bose-Einstein. Todos los átomos tienen la energía más baja del
sistema.
Dado que para alcanzar el estado de CBE es necesario enfriar
muchísimo los átomos, su velocidad disminuye hasta que su longitud
de onda se hace tan larga que su onda es casi plana. En este punto,
las ondas de todos los átomos enfriados se superponen, formando
una única onda y alcanzando el estado de condensado de BoseEinstein.
Por eso se dice que los átomos se encuentran en el mismo lugar,
porque
todos
son
descritos
por
una
única
onda.
Explicación a través del principio de Incertidumbre
Otra explicación se debe al principio de incertidumbre que enunció
Heisenberg. Este principio afirma que no podemos conocer
simultáneamente la posición y la velocidad de una partícula o átomo.
En el cero absoluto (0 K), un átomo tiene velocidad cero, ya que no
tiene temperatura y por tanto no se mueve. Esto hace que la posición
donde se encuentra el átomo sea muy incierta, conocemos su
velocidad exactamente, con lo que el átomo puede encontrarse en un
volumen muy grande.
El volumen ocupado por un átomo tan frío, es decir, la distribución de
probabilidad de encontrarlo, es tan ancha (ver figura 4) que los
átomos de la trampa se superponen y se unen, formando el CBE.
¿Cuán frío debe estar el condensado de Bose-Einstein?
La temperatura es una medida del movimiento de los átomos de un
sistema. Si lo que se desea es parar los átomos, deberemos bajar la
temperatura lo máximo posible con el fin de alcanzar el valor más
cercano al cero absoluto (0 K).
La temperatura más baja que se encuentra de forma natural en el
universo es de 3 K, que corresponde a la radiación de fondo. Ésta es
una radiación uniforme y de baja energía que se encuentra en
cualquier dirección del universo.
Para conseguir el CBE es necesario enfriar los átomos a una
temperatura muchísimo menor. Normalmente se han usado átomos
de rubidio o sodio y se han debido enfriar a una temperatura de
0,000 000 001 K !!!
Propiedades de la materia en estado de CBE
Después de 77 años de que fuera predicho el estado de CBE, Eric
Cornell, Wolfgang Ketterle y Carl Wieman fueron galardonados en
2001 con el premio Nobel de Física por la obtención en 1995 de la
condensación de Bose-Einstein utilizando gases atómicos diluidos, así
como por sus estudios sobre las propiedades que muestra la materia
cuando se encuentra en este estado.
Según declaraciones de Weiman (el constructor de la nevera que ha
sido capaz de alcanzar los 0,000 000 001K), los átomos enfriados
sufren esta transición al estado CBE que las ecuaciones dicen que
pasa. Es como una propiedad de la materia y, a la vez, tan contrario
a la intuición, que parece magia.
Algunas de estas propiedades que muestran los átomos en estado de
CBE son las siguientes:
1. Los átomos están congelados, todo lo quietos que permiten las
leyes de la mecánica cuántica. La interacción entre ellos es muy débil
y entonces puede estudiarse el efecto que tiene sobre ellos la
gravedad.
Los resultados muestran que estos átomos se caen como si fueran
una roca (a escala atómica), pero siguen siendo un gas!! Se
comportan como un sólido, pero no lo son... Por eso a veces al estado
de CBE se le ha denominado hielo cuántico.
2. Los átomos son coherentes, forman una única onda, como la luz
láser. Los átomos del CBE son a los normales como la luz láser a la
de una bombilla casera.
3. Un grupo de átomos en CBE se comporta muy extrañamente ante
la interacción con otro grupo de átomos diferente también en estado
de CBE.
Cuando se pone 2 átomos normales uno encima del otro, se obtiene
el doble de átomos. Hasta aquí, bien. Pero si se coloca un
condensado de Bose-Einstein encima de otro, deja de haber átomos
en esa región!!
Todas estas propiedades de la materia y otras en estado de CBE
siguen siendo estudiadas. Actualmente existen en el mundo veinte
grupos experimentales con capacidad para crear y manipular
condensados de Bose-Einstein. Ya veremos qué nos depara todo esto.
Propiedades
de
la
materia
en
estado
de
CBE
Se ve como una pequeña masa en el fondo de una trampa
magnética. Como una gota de agua que se condensa cuando se enfría
el aire.
Los tamaños obtenidos de CBE más grandes son del tamaño de una
pepita de melón. En la generación de un condensado de BoseEinstein, como aún suele haber átomos normales alrededor, el
condensado suele mostrarse como si fuera la semilla dentro de una
cereza.
En principio, un condensado de Bose-Einstein se puede mirar con
nuestros ojos en el experimento. Sin embargo, como suele ser
pequeño, tendríamos que usar un microscopio e iluminar la muestra
con luz, con lo que le volveríamos a comunicar energía (y por lo tanto
temperatura), se calentarían y volverían a ser átomos normales de
gas.
Como Weiman y Cornell lo vieron por primera vez fue apagando la
máquina durante un instante y tomando una fotografía.
La imagen más famosa de la formación del condensado de BoseEinstein es una imagen que recoge los datos tomados por estos
científicos a medida que la temperatura decrecía.
En la curva de la izquierda podemos ver diferentes colores que son
átomos con distintas temperaturas. El color amarillo representa la
temperatura más elevada, el verde una temperatura algo menor, el
azul aún más frío y el blanco, que representa la temperatura más
baja.
Al principio hay muchos átomos con temperatura alta pero, a medida
que el sistema se va enfriando (de izquierda a derecha en la imagen),
los átomos se van solapando, hasta que forman un único pico, que
representa el momento en que hacen la transición de gas a
condensado
de
Bose-Einstein.
Algunas aplicaciones
Es muy difícil hablar de las aplicaciones de un tipo de estado en la
materia que no ha sido suficientemente estudiado ni controlado. Sin
embargo, ya se han comentado algunos usos:
- Láser de átomos: para construcción de nano-estructuras, es decir,
objetos de un tamaño muy pequeño (de nanómetros).
- Relojes atómicos: para realizar medidas muy precisas del tiempo.
- Detección de la intensidad del campo gravitatorio: con el fin de
buscar petróleo
Esperemos que un descubrimiento tan magnífico no sea utilizado una
vez más para el enriquecimiento de grandes multinacionales, sino
para avanzar en el camino del conocimiento de lo que nos rodea.
Pequeño glosario de términos científicos
Fotón
La luz puede comportarse como una partícula (un fotón) o una onda,
dependiendo del experimento que se esté observando.
La luz se comporta como un fotón cuando choca contra objetos (por
ejemplo, un detector), y se comporta como una onda cuando
podemos observar fenómenos de interferencia (en la que dos ondas
se suman o se restan). Ambas cualidades de la luz son bastante
opuestas e irreconciliables, y no se manifiestan simultáneamente.
Este comportamiento de la luz se denomina "dualidad ondacorpúsculo" y le ocurre no sólo a la energía electromagnética, sino
también a la materia.
Átomos. Dualidad onda-corpúsculo
En su explicación más clásica, están compuestos por un núcleo muy
pequeño y duro, formado por protones (partículas con carga positiva)
y neutrones (partículas sin carga), rodeado por una nube de
electrones (partículas con carga negativa).
Sin embargo, al igual que la luz, los átomos se comportan a veces
como si fueran una onda, y otras veces como si fueran un cuerpo
duro. Es lo que se denomina la dualidad onda-corpúsculo.
Visualizado como un cuerpo, el átomo es un objeto prácticamente
vacío. Si hacemos una comparación con un objeto de nuestro entorno
cotidiano con el fin de visualizar intuitivamente su tamaño, podemos
imaginar un campo de fútbol con un alfiler clavado en el centro. La
cabeza del alfiler sería el núcleo del átomo y los bordes del campo la
distancia a la que está girando la nube de electrones. Dado que la
materia que somos está construida con estos componentes básicos,
podemos decir que nosotros mismos estamos prácticamente vacíos.
Visualizando el átomo como una onda, podemos decir que su estado
puede describirse mediante una función de onda y su posición
mediante una distribución de probabilidad. Esto nos indica que nunca
tenemos certeza en el conocimiento de la posición de un átomo, sólo
sabemos dónde se encuentra probablemente. Por otro lado, el
conocimiento simultáneo de la posición y la velocidad de un átomo
está limitado por el Principio de Indeterminación de Heisenberg.
Considerando el comportamiento ondulatorio de un átomo, como
puede describirse como una onda, podemos asignarle valores a
algunos de los parámetros que definen una onda: la longitud de onda
(l) y la frecuencia de oscilación (n).
La longitud de onda (l) es la distancia que hay entre dos picos de una
onda y la frecuencia (n) está asociada a la rapidez del movimiento de
la onda.
Como podemos ver en la figura 3, cuanto más corta sea su longitud
de onda, más rápido oscilará un átomo y mayor será su frecuencia. Y,
al contrario, cuando más larga sea la longitud de onda de un átomo,
más lento se moverá y más pequeña será su frecuencia. Es de
esperar que para temperaturas muy bajas, la velocidad del átomo
será muy muy pequeña y su longitud de onda sea enorme,
prácticamente una línea.
Principio de Incertidumbre de Heisenberg
Establece que es imposible conocer "simultáneamente" la velocidad y
la posición de una partícula o un átomo.
Para poder medir ambas magnitudes en un átomo, tendríamos que
"pararlo", es decir que su velocidad fuera cero. En ese momento,
sabríamos su posición (porque está parado) y su velocidad (que sería
cero). Hacer que un átomo se pare equivale a conseguir que su
temperatura sea 0 Kelvin, y esto contradice el tercer principio de la
termodinámica.
Figura 4
En la figura anterior se muestran las distribuciones de probabilidad en
tres casos:
(a) Caso normal: el átomo tiene una cierta velocidad y, por tanto,
una cierta probabilidad del ser encontrado en la zona que se marca
con
la
flecha
horizontal.
(b) Caso de conocer la posición del átomo: La curva marca un pico
allí donde está localizado el átomo, aunque la velocidad es
desconocida.
(c) Caso de conocer la velocidad del átomo: La curva muestra que no
es posible determinar ninguna zona pequeña donde localizar el
átomo. Éste estará en cualquier lugar con posibilidades parecidas.
Tercer principio de la termodinámica. Temperatura.
La termodinámica es a la física lo que los jueces a nuestro mundo
cotidiano: establece las leyes que han de cumplirse sin excepciones.
Existen tres principios termodinámicos que ningún proceso físico, sea
del campo que sea, puede romper. El tercer principio establece que
no es posible llegar al cero absoluto de temperaturas. La temperatura
cero kelvin es inalcanzable puesto que las dificultades técnicas nos
impiden llegar.
La temperatura es una medida del movimiento de los átomos que
componen un sistema. En un sólido, los átomos vibran adelante y
atrás, en un gas los átomos vuelan alrededor como pequeñas bolas.
Todo vibra constantemente.
Para medir la temperatura en física se utiliza la "Escala Absoluta"
también llamada "Escala Kelvin (K)". La definición de esta escala está
relacionada con el movimiento de los átomos pues a 0 K todos los
átomos se encuentran a velocidad cero, parados.
Existen otras escalas de temperatura, como Fahrenheit o Celsius
(centígrada), cuyas definiciones están basadas en otro tipo de
eventos de la naturaleza. Por ejemplo, la escala Celsius, que es la
más usada en Europa, está relacionada con la solidificación del agua,
ya que a 0ºC el agua líquida se convierte en hielo. Es una escala más
útil para los procesos físicos que vivimos cada día.
En esta figura podemos ver cómo se corresponden diferentes
temperaturas conocidas según las escalas Kelvin y Celsius. La
temperatura más baja natural en el universo son 3 K, que es la
llamada radiación de fondo. Esta radiación uniforme y de baja energía
se encuentra presente en cualquier dirección del universo. Es
detectable por sensores en radiofrecuencia y es la evidencia más
fuerte que tenemos de que el Big Bang realmente ocurrió.
1.1.4.- Cambios de Estado.
La materia es todo lo que ocupa un lugar en el espacio, por tanto,
incluye todo lo que se ve alrededor y aun aquello que está más allá
de lo que percibe la vista, aunque presente características diversas,
ya que existe en diferentes estados de agregación molecular.
La tierra y los objetos que se presentan en estado sólido, el agua de
los lagos y otras sustancias en estado líquido y la mezcla de aire que
normalmente se encuentra en estado gaseoso, son ejemplos de la
diversidad de estados que asume la materia.
Como se ve, la materia se presenta básicamente en estado sólido,
líquido o gaseoso; ocurren cambios de uno a otro estado, sin que se
altere su composición interna; ejemplo de esto es lo que sucede con
el agua al ser sometida a diferentes temperaturas.
Los cambios que se presentan de un estado a otro son los siguientes:
Fusión:
Es el cambio que presentan los sólidos al convertirse en líquidos
cuando se someten a un aumento de temperatura; por ejemplo, la
fundición de los metales en los altos hornos o el hielo que se funde en
los polos al llegar la primavera.
Solidificación:
Es el cambio del estado líquido al sólido; por ejemplo, cuando se
congela el agua o cuando se deja enfriar la manteca de puerco.
Sublimación :
Es el cambio del estado sólido al gaseoso y viceversa, sin pasar por el
estado líquido; ejemplos de este tipo son la sublimación del yodo y la
naftalina.
Evaporación:
Es el cambio que se presenta cuando se pasa del estado líquido al
gaseoso; por ejemplo, el agua cuando hierve y se convierte en vapor
o la evaporación de la acetona cuando se deja destapado el frasco
que la contiene.
Condensación y licuefacción:
Son los cambios del estado gaseoso o
vapor que cambia a líquido recibe el
ejemplo: las nubes al precipitarse en
que se transforma en líquido se le
cuando el oxígeno, que es un gas, se
medicinales.
vapor al líquido. Si se trata de
nombre de condensación, por
forma de lluvia. Si es un gas
denomina licuefacción, como
convierte en líquido para fines
1.1.6.- Base experimental de la teoría cuántica y estructura atómica.
La teoría cuántica apareció ante la necesidad de una mejor descripción de las
propiedades de la energía radiante (luz). Por tanto iniciaremos estudiando las
características de la energía radiante. Todos los tipos de energía radiante, también
llamadas radiación electromagnética, se mueve a través del vacío a una velocidad de
2.9979250 x 108 m/s, la "velocidad de la luz". La velocidad de la luz es una de las
constantes físicas conocidas con mayor exactitud. La energía radiante tiene
características de onda semejantes a las de las olas que se mueven en el agua, las cuales
son el resultado de la energía que se imparte, posiblemente tirando una piedra, por el
movimiento de un bote, o la fuerza del viento sobre la superficie del agua. Esta energía
se expresa como el movimiento del agua hacia arriba y hacia abajo. Un corcho que se
encuentra en la superficie del mar no se mueve lateralmente, sólo hacia arriba y abajo
con el movimiento de las olas.
Si observamos el corte transversal de una ola (figura 1.1), vemos que es periódica. El
patrón de los picos y las depresiones se repite a intervalos regulares. La distancia entre
picos (o depresiones) sucesivos se llama longitud de onda. El número de longitudes de
onda completas que pasan por un punto determinado en 1 segundo es la frecuencia de
la onda. Podemos medir la frecuencia de una ola contando el número de veces por
segundo que el corcho se mueve hacia arriba y hacia abajo en un ciclo completo.
Fig.1.1 Caracerísticas de una onda de energía radiante.
En forma similar, podemos asignar una frecuencia y una longitud de onda a la energía
radiante. Igual que en el caso de la ola la frecuencia de la radiación es el número de
longitudes de onda completas, o ciclos que pasan por un punto en 1s. Como toda la
energía radiante se mueve a la velocidad de la luz, la longitud de onda y la frecuencia
están relacionadas entre sí. Si la longitud de onda es larga habrá menos ciclos de la onda
pasando por un punto en un segundo, y la frecuencia será baja. En cambio, si una onda
tiene frecuencia alta, la distancia entre los picos de la onda debe ser pequeña (la
longitud de onda es corta). Esta relación inversa entre la frecuencia y la longitud de
onda de la energía radiante se puede expresar en una ecuación sencilla. El producto de
la frecuencia, v (nu), por la longitud de onda,
luz, c.
v
(lambda), es igual a la velocidad de la
=c
Ec. 1
¿Por qué las diferentes formas de energía radiante tienen propiedades muy diferentes?
Podemos caracterizar los diversos tipos de energía radiante por sus longitudes de onda.
Podemos ver que abarcan un intervalo muy grande. Las longitudes de onda de los rayos
cósmicos son similares a los diámetros de los núcleos atómicos, mientras que las ondas
de radio pueden ser más grandes que un campo de fútbol. La unidad de longitud
seleccionada normalmente para expresar la longitud de onda depende del tipo de
radiación, como se ilustra en la figura 1. La frecuencia se expresa en ciclos por segundo,
unidad que también se llama hertz (Hz). En general, los "ciclos" se sobreentienden, así
que las unidades de frecuencia son "por segundo", lo cual se indica por s -1 o 1/s. Por
ejemplo, una frecuencia de 820 kilohertz (kHz), característica para una estación de radio
AM, se podría escribir como 820,000 s-1.
Tabla 1 Unidades comunes de longitud de onda para la radiación
electromagnética
Unidad
Símbolo
Longitud (m)
Tipo de radiación
Angstrom
Å
10-10
Rayos X
Nanómetro
nm
10
-9
Ultravioleta,
visible
Micrómetro
m
10-6
Infrarrojo
Milímetro
mm
10-3
Infrarrojo
Centímetro
cm
10-2
Microondas
Metro
m
1
TV, radio
Ejercicio de muestra 1
La luz amarilla emitida por una lámpara de sodio tiene una longitud de onda de 589 nm.
¿cuál es la frecuencia de esta radiación?
Solución: podemos reacomodar la ecuación 1, para obtener v = c/
valores de c y
. Substituyendo los
y convirtiendo los nanometros en metros, obtenemos:
Podemos ver la luz visible debido a las reacciones químicas que provoca en nuestros
ojos. También estamos familiarizados con los efectos de otras formas de radiación. Por
ejemplo, la sobreexposición de alguna parte del cuerpo a radiación infrarroja (calor)
puede ocasionar una quemadura; la sobreexposición a la luz ultravioleta puede causar el
bronceado al sol o una quemadura por el sol y la sobreexposición a los rayos x puede
ocasionar daños a los tejidos, incluso cáncer. Esta diversidad de efectos se debe a
diferencias en la energía de la radiación de alta frecuencia (y por consiguiente de
longitud de onda corta) tiene más energía que la radiación de menor frecuencia (y por
tanto de mayor longitud de onda). La relación cuantitativa entre la frecuencia y la
energía fue desarrollada hace aproximadamente cien años en la revolucionaria teoría
cuántica del físico alemán Max Planck
1.1.7.- Radiación de cuerpo negro.
Un cuerpo negro se define como aquel que absorbe todo el calor radiante que recibe. Tal
absorbente perfecto será también un emisor perfecto.
La relación entre el calor radiante E emitido por un cuerpo y su temperatura fue
establecida primero por los extensos experimentos de laboratorios de Josef Stefan. La
misma ley fue deducida después a partir de consideraciones teóricas por Ludwig
Boltzmann, y ahora se conoce como la ley de Stefan-Boltmann.
E = Kt4
Ec. 2
Aquí E representa la energía radiada por segundo por un cuerpo a una temperatura
absoluta T, y k es una constante de proporcionalidad. La ley sólo se aplica a los
llamados "cuerpos negros". Si E representa el calor, en kilocalorías, radiado por metro
cuadrado y segundo, tendremos:
k = 1.3567 x 10-11 Kcal/m2SK4
Si E representa la energía radiada por metro cuadrado y segundo, en Joule, será:
k = 5.670 x 10-8 J/m2sK2
Definida así k, podemos escribir la ley de Stefan-Boltzmann poniendo:
E = Kt4A
Ec. 3
donde A es el área en metros cuadrados y
es el tiempo en segundos.
La mejor aproximación de laboratorio a un cuerpo negro, es el agujero en una caja
ennegrecida. Prácticamente, todo el calor que entre por tal agujero será absorbido en el
interior. El terciopelo negro o una superficie pintada mate con negro de humo
absorberán cerca del 97 % del calor radiante que cae sobre él, y puede considerarse para
muchos propósitos como un cuerpo negro. Sin embargo, las superficies metálicas
pulidas, lejos de ser cuerpos negros, tan sólo absorben cerca del 6 % de la energía
incidente y reflejan el resto. La mayoría de las sustancias tienen grados de absorción
entre dos extremos.
Ejercicio de muestra 2
Una bola de cobre de 20 cm de diámetro se recubre de negro de humo y se calienta a
una temperatura de 727 0C. (a) ¿Qué cantidad de calor radiará este cuerpo en 5 s? (b) Si
las paredes de la habitación están a 27 0C, ¿qué cantidad de calor absorberá este cuerpo
en ese mismo tiempo? Suponga que se trata de un caso de radiación de cuerpo negro,
tanto en (a) como en (b).
Solución: Si pasamos estos datos al sistema MKSA tendremos T = 727 + 273 = 10000
K, A = 4 p r2 = 0.1257 m2;
= 5 s y k = 1.3567 x 10-11 Kcal/m2 s 0K4. Sustituyendo
luego estas cantidades directamente en la Ec. 3, obtenemos para la pregunta (a):
E = Kt4A
= 1.3567 x
(0.1257) (5)
= 8.527 Kcal
10-11
(1000)4
En el lenguaje y la teoría de la mecánica cuántica, un cuerpo negro, es
una sustancia negra ideal que absorbe todas y no refleja ninguna de la energía
radiante que baja en ella. El negro de humo, o el carbón pulverizado, que
refleja menos el de 2% de la radiación que baja en él, aproxima un cuerpo
negro ideal. Puesto que un cuerpo negro es un amortiguador perfecto de la
energía radiante, por los leyes de la termodinámica debe también ser un emisor
perfecto de la radiación.
A finales del siglo XIX, los científicos sabían que el color de la luz que
emite un cuerpo –la gama de sus longitudes de onda– está relacionado con el
material del que está hecho el objeto y con su temperatura. Hablando en
general, la luz azul, con longitudes de onda muy cortas, es la que prevalece en
el espectro de los objetos muy calientes; las longitudes de onda rojas, o más
largas, indican menos calor. Hay representadas también otras longitudes de
onda, pero como regla general, cada temperatura se relaciona con una longitud
de onda dominante, que proporciona al objeto resplandeciente un color
característico. Para simplificar su análisis de la radiación, los teóricos del siglo
XIX habían conjurado el cuerpo negro. Al contrario que los objetos reales, esta
entidad imaginaria absorbe la radiación de todas las frecuencias, lo cual la
hace completamente negra. También emite radiación de todas las frecuencias,
independientemente de su composición material. Los experimentadores habían
creado ingeniosos dispositivos para aproximar esta construcción teórica a los
laboratorios, y habían aprendido mucho sobre las características de la
radiación del cuerpo negro. Lo que les faltaba era una teoría para predecir la
distribución o forma del espectro de radiación del cuerpo negro, es decir, la
cantidad de radiación emitida a frecuencias específicas a varias temperaturas.
Su formulación se inició en el cambio de siglo con los trabajos de Max
Planck, quién se sentía intrigado por un problema fundamental que tenía que
ver con la radiación del denominado cuerpo negro.
Hasta ese entonces, la mayoría de los científicos creían que la clave de
este problema se hallaba en comprender la interacción entre radiación
electromagnética y materia. En 1900, cuando Planck atacó el problema, aceptó
la teoría electromagnética de la luz que sostenía que la luz era un fenómeno
ondulatorio y que la materia –que se suponía que contenía pequeños cuerpos
cargados eléctricamente, o partículas– irradiaba energía en la forma de ondas
de luz cuando esas partículas cargadas eran aceleradas. La sabiduría
aceptada decretaba también que la cantidad de energía radiada por una
partícula cargada acelerada podía situarse en cualquier parte a lo largo de una
gama continua.
Con el propósito de estudiar la radiación de un cuerpo negro, Planck
imaginó las partículas cargadas como diminutos reguladores y sencillos
repetidores, con características osciladoras, aceleradoras y desaceleradoras,
como si estuviesen unidos a un muelle ingrávido. Hasta ese momento, se
mantenía firmemente dentro del reino de la física del siglo XIX. Pero a partir de
ahí se desvió radicalmente.
En el camino de calcular el equilibrio de energía entre los supuestos
osciladores y su radiación de entrada y salida, Planck halló que necesitaba
suponer la existencia de cuantos, o ciertas pequeñas divisiones de energía,
antes que una gama continua de posibles energías. Definió un cuanto de
energía como la frecuencia de la oscilación multiplicada por un número
diminuto que no tardó en ser conocido como la constante de Planck. Luego
utilizó estas suposiciones para resolver el problema del cuerpo negro; su
solución matemática predijo perfectamente la radiación del espectro del cuerpo
negro.
Ahora bien, de acuerdo a ese descubrimiento de Planck la distribución
de la energía radiante del cuerpo de un radiador negro según la longitud de
onda, depende de la temperatura absoluta del cuerpo negro y no de su
naturaleza o estructura interna. Mientras que la temperatura aumenta, la
longitud de onda en la cual la energía emitió por segundo, son las
disminuciones de un máximo. Este fenómeno se puede considerar en el
comportamiento de un objeto incandescente ordinario, que emite su radiación
máxima en longitudes más cortas de onda mientras el ente llega a ser más
caliente. Primero brilla intensamente en longitudes de onda rojas largas,
entonces en longitudes de onda amarillas, y finalmente en longitudes de onda
azules cortas.
En termodinámica el principio del cuerpo negro se utiliza para determinar
la naturaleza y la cantidad de la energía emitida por un objeto calentado. La
radiación del cuerpo negro ha servido como una fuente importante generadora
de evidencias sobre la factibilidad de la teoría del Big Bang, la cual sostiene
que el universo emergió de una ardiente explosión hace unos 15 mil millones
de años. Según esta teoría, la explosión debió haber dejado a un cuerpo negro
el remanente de la radiación cósmica de fondo que es uniforme en todas las
direcciones y que debería tener una temperatura promedio cercana a los 3° K.
Cuestión que fue comprobada en 1964 por Arno A. Penzias y Roberto L y que
arrojó una temperatura de 2,7°K. Últimamente, la NASA ha logrado recopilar
nuevos datos sobre esa radiación usando el satélite COBE, que han revelado
fluctuaciones pequeñas de la temperatura en la radiación, que han sido
atribuidas al «embrionage» tanto de estrellas como de galaxias.
Las ondas de radio, las radiaciones infrarrojas, la luz visible, la luz
ultravioleta, los rayos X y los rayos gamma, constituyen las distintas regiones
del espectro electromagnético.
Ahora bien, sobre la superficie de un cuerpo incide constantemente en
ella energía radiante, tanto emanada del interior del cuerpo como recibida
desde el exterior, la que llega desde el exterior procede de los objetos que
rodean al cuerpo. Cuando la energía radiante incide sobre la superficie una
parte de ella se refleja y la otra parte se transmite.
En el dibujo de la izquierda, hemos intentado graficar la energía radiante que
incide desde el exterior sobre la superficie de un cuerpo. Si su superficie es lisa
y pulida, como la de un espejo, la mayor parte de la energía incidente se
refleja, el resto atraviesa la superficie del cuerpo y es absorbido por sus átomos
o
moléculas.
Si r es la proporción de energía radiante que se refleja, y a la proporción que se
absorbe, se debe de cumplir que r + a = 1.
Una idéntica proporción de energía radiante r que incide desde el interior se
refleja hacia dentro, y se transmite la proporción a = 1 - r que se propaga hacia afuera ,
la que es conocida como energía radiante emitida por la superficie.
En el dibujo de la derecha, se grafica el comportamiento de la superficie de un cuerpo
que refleja una pequeña parte de la energía incidente. Las anchuras de las distintas
bandas corresponden a cantidades relativas de energía radiante incidente, reflejada y
transmitida
a
través
de
la
superficie.
Ahora bien, si analizamos ambos gráficos precedentes, podemos concluir que
un cuerpo con buena absorción de radiación es, a su vez, un buen emisor, así
como un mal absorbedor es un mal emisor. También podemos señalar, que un
buen reflector es un mal emisor, y un mal reflector es un buen emisor.
Una aplicación práctica de ello la podemos observar en los termos
caseros que son utilizados para mantener la temperatura de los líquidos que se
almacenan en ellos. Esos termos constan, generalmente, de una doble pared
sellada de vidrio que, al momento de su construcción, el espacio entre ambas
paredes fue vaciado del aire que contenían para evitar las pérdidas por
conducción y convección. Para reducir las pérdidas por radiación, se cubren las
paredes con una lámina de plata que es altamente reflectante y por tanto, mal
emisor y mal absorbedor de radiación.
Teóricamente, la
superficie de un
cuerpo
negro
configura un caso
límite, en el que
toda la energía
incidente llegada
desde el exterior
es absorbida, y
toda la energía
incidente
generada en el
interior
es
emitida.
Hemos hablado de teoría, dado que un cuerpo negro es
una concepción teórica y en la naturaleza no se
conocen entes con esas extremas propiedades, ya que
incluso el negro de humo refleja menos del 2% de la
energía incidente.
No obstante no importa que tal
cuerpo idealmente negro no
exista en la naturaleza; puede ser
representado
artificialmente,
gracias
a
radiaciones
que
escapan por una estrecha
abertura de un recinto cerrado,
cuyas paredes están mantenidas
a una temperatura rigurosamente
uniforme e invariable. La energía radiante incidente a
través de la abertura, es absorbida por las paredes en
múltiples reflexiones y solamente una mínima proporción
escapa (se refleja) a través de la abertura. Podemos por
tanto decir, que toda la energía incidente es absorbida.
La Radiación del Cuerpo Negro
Ya anteriormente señalamos que hasta los finales del siglo XIX, la teoría
sobre las ondas de la luz era la imperante, pues con ella se podían explicar la
mayoría de los fenómenos que comportaba la luz. Sin embargo, había algunas
excepciones notables. Una de ellas era la asociada al la radiación de un cuerpo
negro, que es la característica radiación que un cuerpo emite cuando se ha
incrementado su temperatura. En ese tiempo, ya se sabía que la energía total
de la radiación crece proporcionalmente a la cuarta potencia de la temperatura
del cuerpo negro. Si
se mide para cada longitud
de
onda
la
intensidad de los
rayos correspondientes, como hicieron con notable exactitud Lummer y
Pringsheim en 1899, llevando –en un sistema de coordenadas– las primeras a
las abscisas y las segundas a las ordenadas, se obtiene para cada temperatura
dada una curva en forma de campana. Las ramas de la curva se aproximan
asintóticamente al eje horizontal, y presentan un máximo cuya posición se
desplaza, con temperaturas crecientes, de las longitudes de ondas mayores a
las menores, de acuerdo con la ley descubierta por Wilhelm Wien en 1894.
La radiación cambia en la naturaleza con los cambios de temperatura. Los
experimentos de «cuerpos negros» (emisión - absorción) muestran curvas
como la graficada a la izquierda sobre la intensidad de la radiación (energía
emitida por tiempo y área) con respecto a la temperatura T de la longitud de
onda.
Ahora bien, si se aplica al problema de la radiación de un cuerpo la teoría
ondulatoria de la luz, ésta colapsa, ya que predice que la intensidad I, para una
temperatura dada es:
[01]
I
lo que arroja un resultado que implica que la teoría sí funciona en
experimentaciones orientadas a longitudes de onda largas, pero no así cuando
se trata de aplicarla a longitudes de onda cortas, ya que otorga resultados
disímiles a lo que realmente sucede. Lo último, se ilustra en el siguiente gráfico.
PREDICCIÓN
CLÁSICA DE LA
RADIACIÓN
DE
UN
CUERPO
NEGRO
En consecuencia ¿Cuál es la ley que rige la marcha general de esta
curva empírica? ¿La ley que permite prever la intensidad de la radiación para
cada longitud de onda y para cada temperatura?
Hasta los años finales del siglo XIX, ningún físico fue capaz de dar una
respuesta satisfactoria. La fórmula propuesta, en 1896, por Wien se aplicó, en
las temperaturas corrientes, solamente a las ondas cortas; la curva propuesta,
en 1900, por los ingleses Rayleigh y Jeans, a ondas largas. Hubo dos fórmulas,
y aunque se las pudiera aceptar ambas, ninguna coincidió, en las longitudes
medias de ondas, con la curva experimental, dejando así abierto el enigma de
la distribución energética de la gama visible del espectro. Más aún, la ley de
Rayleigh - Jeans preveía que en todas las temperaturas la energía del conjunto
de las radiaciones tendría valor infinito: consecuencia absurda, reveladora de
una hipótesis ilícita, camuflada con las premisas de los cálculos.
Max Planck, en esos mismos años del siglo XIX, estudió y analizó la
absurda conclusión a la que llegaban un conjunto coherente de ideas básicas,
hasta entonces nunca puestas en duda, sobre la radiación de un cuerpo.
Comprendió que la solución al problema exigía la introducción de una nueva
hipótesis; se atrevió a eliminar la suposición de que en el cuerpo radiante los
osciladores incidentes pueden emitir luz de cualquier frecuencia; negó que la
energía intercambiada pudiese ser dividida ilimitadamente; supuso que el
átomo emite radiación de manera discontinua, en cantidades finitas, en
minúsculos manojos.
En su idea matriz, Planck deduce que ello ocurre como si el átomo,
después de haber irradiado un tren de ondas, se detuviera antes de irradiar
otro. Así, la radiación –y como no se tardó en reconocer, en general, cada
intercambio energético– posee una estructura discontinua, de índole
cinematográfica, produciéndose en granos, por saltos bruscos, por cuantos, La
más pequeña cantidad de energía E que un átomo puede emitir o absorber es
un cuanto elemental. Este es proporcional a la frecuencia f del oscilador
atómico y posee el valor E = nhf, donde el factor de proporcionalidad h, que
debía inmortalizar más tarde el nombre de su descubridor, es una constante
universal. Un átomo no puede adquirir o perder energía que no sea igual a un
número entero de cuantos. Estos se distribuyen al azar entre los osciladores de
la misma frecuencia, y el cálculo de probabilidad decidirá cuántos poseerán la
energía h f, cuántos 2h f, y así sucesivamente. El principio de equipartición está
abolido. Bajo esta condición, la fórmula establecida por Planck conduce a una
exacta interpretación de la radiación del cuerpo negro, a una perfecta
concordancia entre experiencia y teoría.
La fórmula teórica ideada por Planck en el año 1900, sobre la radiación
de un cuerpo negro, como ya dijimos, es aplicable conciliatoriamente para
todas las longitudes de onda. En esta teoría los átomos de un cuerpo no
pueden tener energías arbitrarias sino que por el contrario son cuantizadas. La
magnitud de estas energías es dada por el fórmula:
E = nhf,
[02]
donde n es un número entero = 0.1.2..., f es la frecuencia de la vibración de los
átomos, y h es una constante, ahora llamada la constante de Planck :
[03]
h = 6.63 x 10- 27 J . s .
El valor numérico de esta importantísima constante, en ergios segundos,
el «índice de la discontinuidad» es muy pequeño. Los saltos son, pues, en los
intercambios energéticos, inconcebiblernente minúsculos. En efecto, es
imposible representarse por una imagen una discontinuidad de semejante
grado de fineza. Si una escalera tuviera verticalmente una altura de 150
millones de kilómetros (distancia Tierra–Sol) y cada uno de sus peldaños el
ascenso vertical de 1/10 27 (el denominador de h) de la escalera, habría sobre
25mm un centenar de miles de millones de peldaños.
Sin embargo, no es solamente su extremada pequeñez, sino más aún su
dimensión física la que confiere a la constante de Planck su excepcional
carácter. En efecto, h representa el cociente de una energía por una
frecuencia; puesto que esta última, número de oscilaciones por segundo, es la
inversa de la duración de una oscilación, es evidente que h designa una
magnitud que aparece como el producto de una energía por el tiempo. Tal
magnitud se llama, en física, «acción». Es esta magnitud, la acción, la que
varía con saltos bruscos y la que se nos ofrece en la naturaleza fragmentada
en cuantos. Medida de la discontinuidad de los cambios energéticos, es este
cuanto de acción, h, el supremo regulador, en la escala microscópica, de todos
los fenómenos. Sin duda es una de las más imprevistas sorpresas que nos
ofrece la física moderna, presentando un fragmento infinitesimal de este ente
abstracto que es la acción, como omnipresente en los intercambios de energía.
Por otra parte, en la hipótesis de Planck la distribución espectral de la
radiación es continua y tiene un máximo que depende de la temperatura y se
puede expresar en términos de la longitud de onda, o bien, de la frecuencia de
la radiación. En que, dEf / df es la densidad de energía por unidad de
frecuencia para la frecuencia f de la radiación contenida en una cavidad a la
temperatura absoluta T. Su unidad se expresa (J · m-3) · s.
[04]
donde k es la constante de Boltzmann.
Por otro lado, dE/ des la densidad de energía por unidad de longitud
de onda para la longitud de onda de la radiación contenida en una cavidad a
la temperatura absoluta T. Su unidad se expresa (J · m-3) · m-1
[05]
Por otra parte, siendo la energía una magnitud espacial, h, el cuanto
elemental de acción (energía por tiempo), es, pues, un ente espaciotemporal
tetradimensional. Casi todas las magnitudes fundamentales de la física clásica
son secciones de distintas dimensiones del espaciotiempo, y poseen, en el
sentido einsteiniano, valores relativos. Por el contrario, la constante h es un
valor absoluto. En la retrospección histórica, nos resulta significativo que pocos
años antes que la relatividad se hubiera abierto camino en la física, la
naturaleza había revelado a Planck una trascendental magnitud absoluta.
En la historia de la física del siglo XX, no son muchos los
acontecimientos que puedan ser comparados con el descubrimiento de los
cuantos. Mientras que todos los fenómenos sólo son, en la práctica,
intercambios de energía, el cuanto manifiesta su alcance a través de su
presencia en todos los acontecimientos de la naturaleza. Esta universalidad es
lo que resalta el alcance del descubrimiento de Planck. Hasta ahora, siempre
los físicos parten de ahí para idear los nuevos modelos y teorías sobre la
estructura de la materia y de la radiación, y en general, una parte importante de
sus ideas y realizacions que debían transformar la imagen del mundo físico, se
embrionan en la revolucionaria hazaña del descubridor del cuanto.
1.1.8.- Teoría atómica de Bohr.
El modelo atómico de de Rutherford fue un gran paso en la comprensión de la
estructura atómica; su inconveniente es que no mencionaba nada de los electrones,
excepto que se encontraban fuera del núcleo. Fue en 1913 cuando el físico danés Niels
Bohr propuso un modelo atómico, figura 1.2.1, para explicar la estructura atómica y,
además, dar una explicación sobre el espectro del hidrógeno.
Para explicar su modelo atómico, Bohr fundamentó su teoría en la teoría del cuanto,
propuesta por M. Planck, y se basó en los postulados siguientes:
1. El electrón del átomo de hidrógeno se mueve en órbitas circulares y definidas de
energía alrededor del núcleo. Las órbitas también reciben el nombre de niveles
energéticos o cuánticos, representados por la letra n, que toma valores desde 1,
2, 3, ...
2. Los electrones que se mueven en órbitas definidas no emiten energía.
3. Un lectrón puede pasar de una a otra órbita o nivel energético, siempre y cuando
absorba o emita la energía necesaria.
4. Dentro de sus órbitas o niveles de energía, los electrones se mueven en tres
dimensiones espaciales formando una nube electrónica.
En el modelo atómico de Bohr, el electrón del átomo de hidrógeno se encuentra en el
nivel de energía más bajo (n=1), también llamado estado fundamental. Al hacerle llegar
una radiación, absorbe un cuanto de su energía y pasa a ocupar un nivel energético
superior, figura 1.2.1.
Cuando un electrón regresa de un nivel energético superior a uno inferior emite
la energía absorbida en forma de radiación dando origen a las series espectrales del
hidrógeno, figura 1.2.2.
La teoría de Bohr tiene validez para el átomo de hidrógeno, no así para átomos más
complejos. Sin embargo, algunos conceptos de su teoría continúan siendo válidos
actualmente. Por ejemplo:
1. En el espacio que rodea al núcleo sólo son permisibles ciertos niveles
energéticos.
2. Los electrones que rodean al núcleo tenderán a ocupar los niveles energéticos de
menor energía en el estado fundamental del átomo.
Con el mejoramiento de las mediciones espectroscópicas, coincidiendo con el
tiempó en que Bohr publicó su teoría, se reportaron espectros atómicos con una
estructura más fina; es decir, las líneas esoectrales que en un principio parecían ser una
sola, resultaron estar formadas por otras más delgadas. Para explicar ese fenómeno fue
necesario hacer modificaciones al moelo atómico de Bohr, de acuerdo con el cual las
órbitas electrónicas son circulares.
Fig. 1.2.1 Modelo atómico propuesto por Bohr para el átomo del hidrógeno.
Fig. 1.2.2 Transición del electrón en los
diferentes niveles de energía para
formar las diferentes series espectrales.
La teoría de Bohr (1913) sobre el átomo de hidrógeno (el más sencillo) consistía
en suponer que los estados energéticos del átomo son órbitas que el electrón describe al
rededor del núcleo; con las limitaciones impuestas por la teoría de los cuantos de
Planck.
1.1.9.- Estructura atómica: Principio de Dualidad, Principio de Incertidumbre,
Función de onda, Principio de Afbau, Principio de Exclusión de Pauli.
Estructura del Atomo
¿Cómo se diferencian los átomos de elementos distintos? ¿Por qué ciertos átomos se
unen en una manera determinada mientras que otro no? ¿Qué es lo que mantienen
unidos a los átomos en las moléculas? Estas preguntas se pueden responder solamente
en función de la estructura atómica. Los átomos no son partículas indivisibles como lo
había pensado originalmente Dalton, sino que están compuestos de partículas más
simples: en el núcleo del átomo los neutrones y los protones cargados positivamente y
rodeando al núcleo los electrones cargados negativamente.
El Electrón.
Es una partícula subátomica que tiene carga negativa . Los trabajos de J.J. Thomson y
R.AS. Millikan han suministrado una descripción básica del electrón: una partícula con
una carga negativa de -1.6x10-19 C (C=Coulomb); esta cantidad de carga con frecuencia
se representa por símbolo e; tiene una masa de 9.11x10-31 kg. Debido a que el electrón
tiene la carga eléctrica más pequeña hasta ahora conocida, se le usa como referencia
para todas las otras particulas cargadas; por consecuencia decimos, que la carga del
electrón es -1. Por ejemplo, cuando se dice que una particula tiene una carga +3,
significa una carga de +3(1.6x10-19) C. El + indica que es de signo opuesto a la carga
del electrón y el 3 significa que es 3 veces más grande.
La masa del electrón en la escala de masa atómica (isotopo del Carbono -12) es
0.000544874 uma. Este número es tan pequeño que generalmente se le aproxima a un
valor cero.
El Protón
Es una partícula cargada positivamente, la carga del protón es igual a la carga del
electrón en magnitud, peso de signo opuesto, es decir, +1.60x10-19 C. Su masa es igual a
1.673x10-27 kg, correspondiente a un valor de 1.007595 uma.
El Neutrón
Se define como una partícula subátomica neutra, con una masa de 1.675x10 -27 kg,
correspondiente a un valor de 1.00866544 uma.
El Núcleo
Es la parte central del átomo cargada positivamente. Esta compuesto principalmente de
las partículas fundamentales llamadas protones y neutrones. Los electrones se mueven
alrededor del núcleo. El núcleo contiene la mayor parte de la masa.
Número Atomico y Número de Masa .
Un átomo se puede identificar por dos números: el número atómico, Z, y el número de
masa, A.
El número atomico (Z) es igual al número de protones que hay en el núcleo de un átomo
y es igual a la carga positiva en el núcleo. El número atómico es característico del
elemento.
El número de masa (A) es la suma del número de protones y de neutrones en el núcleo.
Es el número entero máss próximo a la masa atómica. Si se representa por N el número
total de partículas en el núcleo será:
A= Z+N
Isotopos
Son átomos que tienen el mismo número de protones (mismo número atómico) pero
diferente número de neutrones, osea diferente número de masa. El número de neutrones
sera: A-Z
La mayoria de los elementos no existen como un isotopo sencillo sino que son una
mezcla de isotopos; por esa razon las masas son realmente masas atómicas promedio.
La Dualidad Onda- Partícula de la Materia
En 1924, Luis de Broglie sugirió que así como para explicar el efecto fotoeléctrico fué
necesario considerar que la luz tenía, ademá de naturaleza ondulatoria, una naturaleza
corpúscular al presentarse en forma de fotones, en algunas circunstancias cualquier
partícula material se podia tratar como si fuera de naturaleza ondulatoria. De Broglie
aplicó su teoría sobre el comportamiento ondulatorio de los electrones al átomo de
hidrógeno y creó un modelo en el cual las órbitas fueron remplazadas por ondas
estacionarias que se ajustaban exactamente a las circunferencias que había calculado
Bohr.
En 1926, la teoría ondulatoria de la materia fué confirmada experimentalmente, pues un
haz de electrones fué difractado al atravesar una lámina muy delgada del material
cristalino, como una hoja de papel de aluminio.
PRINCIPIO DE INCERTIDUMBRE DE HEISSENBERG.
Un principio fundamental, base de la teoría atómica moderna, refleja la incertidumbre
que hay en las mediciones atómicas. En 1926, Werner Heissenberg expresó que es
imposible conocer con precisión los dos factores importantes que gobiernan el
movimiento de un electrón, que son su posición y su velocidad. Si se determina
experimentalmente su posición exacta en cierto momento, su movimiento es perturbado
en tal grado, por el mismo experimento, que no será posible encontrarlo. Inversamente,
al medir con exactitud la velocidad de un electrón, la imagen de su posición queda
borrada.
Debido al principio de incertidumbre, no es posible decir que los electrones estén en
cierto punto en determinado momento y que se mueven con cierta velocidad; solo puede
hablarse de la probabilidad de encontrar al electrón en cualquier volumen arbitrario
alrededor del núcleo. Las órbitas de Bohr y las ondas estacionarias de De Broglie, deben
ser sustituidas por un modelo preciso: el electrón debe ser considerado como una nube
de carga negativa de densidad variable , que ocupa un lugar en el espacio alrededor del
núcleo. Dentro del espacio en el que puede encontrarse el electrón hay variaciones muy
grandes en las propiedades en las probabilidades, siendo mayores en algunos lugares,
los que se consideran de mayor densidad electrónica. Estos espacios en los que se
mueve el electrón recibe el nombre de órbitales, dentro de los cuales, el electrón tiene
una cantidad específica de energía.
Un concepto fundamental de la mecánica cuántica es que la materia
tiene propiedades ondulatorias. Este carácter de la materia significa que una
partícula como el electrón de un átomo se puede describir mediante una
función de onda, ψ, que es una función matemática de las coordenadas de
posición x, y, z, y del tiempo t. La función de onda describe la distribución de
los electrones en los átomos, y por ello ocupa un lugar central en cualquier
interpretación de las propiedades de los átomos y de los compuestos que
forman.
Para ello se utilizó la sugerencia introducida por el físico francés Louis
de Broglie (1924), quién expresó que una partícula lleva asociada una onda, lo
cual dio origen a la función de onda. Una consecuencia del carácter ondulatorio
de la materia resulta ser "la imposibilidad de especificar, simultáneamente y
con exactitud, la posición y el momento lineal de una partícula". Esta conclusión
fue propuesta por Werner Heisenberg y se conoce como principio de
incertidumbre.
Estas ideas llevaron a Erwin Schrödringer a formular en 1926 la
ecuación que , cuando se resuelve, da una función de onda real. En el caso
simple de una partícula de masa m que se mueve en una dirección del espacio
de energía potencial V, la ecuación es:
ħ2 . d2 
 
2m
dx2
+
V 
=
E
donde ħ2 = h/2 π. Por lo tanto, la ecuación expresa simplemente el
hecho de que la energía total, E, es la suma de la energía cinética y de la
energía potencial V.
Al resolver la ecuación de Schrödringer para una partícula confinada
en una pequeña región del espacio o sometida a una fuerza atractiva (como
ocurre en el electrón de un átomo), se encuentra que se pueden obtener
soluciones aceptables solamente para ciertas energías. Es decir, la energía de
una partícula está cuantizada o limitada a valores discretos.
La cuantización de un observable físico es de gran importancia en
química, porque dota de estabilidad a los átomos y moléculas y determina los
enlaces que éstos pueden formar. Las soluciones aceptables de la ecuación
de Schrödringer para la partícula en una caja son ondas de longitud λ = 2L / n,
donde este tipo de ondas tienen la forma matemática :
ψ = sen 2 π x = sen n π x
λ
L
donde n = 1,2,... El número n es un ejemplo de número cuántico - es el número
cuántico principal- , que toma valores enteros y define la función de onda. Este
número determina las energías permitidas del sistema.
PRINCIPIO DE AUFBAU
El problema que se presenta al explicar las configuraciones electrónicas de la
primera serie de transición es bien conocido.
De acuerdo a la espectroscopía atómica los átomos de estos metales adoptan
en el estado fundamental la configuración (Ar) (4s)2 (3d)n, con excepción del Cr
y el Cu que adoptan la configuración (Ar) (4s)1 (3d)n+1. Al avanzar en la serie
hay al menos un electrón en 4s, cuando aun existen orbitales 3d vacantes,
indicando que el orden de llenado es 4s antes que el 3d.
Los correspondientes iones dipositivos adoptan en toda la serie la
configuración (Ar) (3d)n.
Esto sugiere que los electrones en 3d están unidos más fuertemente al núcleo
que los 4s, siendo más estables y por lo tanto de menor energía, en
concordancia con los cálculos teóricos. Con 4s mayor que 3d la paradoja
aparente es que se obtendría un estado de menor energía ocupando orbitales
de energía mayor.
En muchos libros la discusión cualitativa de esta situación se basa en un
diagrama semejante al de la Figura 3.
Diagrama esquemático de las energías de los orbitales 4s y 3d frente al
número atómico Z en átomos neutros.
Para los elementos del cuarto período la explicación es la siguiente. En el
potasio el orbital 4s tiene menor energía que el orbital 3d y entonces se ocupa
primero. En el calcio ocurre lo mismo y se completa el orbital 4s con dos
electrones. Al llegar al escandio se dice que en este caso 4s es mayor que 3d
y por ello los electrones en 4s se pierden primero por ionización, pero como el
orbital 4s ya tenía dos electrones en el calcio, el tercer electrón se ubica en el
orbital 3d, que ahora es el de menor energía. En algunos casos se ilustra esta
descripción mediante diagramas similares a los que se presentan en la Figura
4.
En estos diagramas la flecha más intensa representa el último electrón
agregado. La principal objeción a la explicación anterior es que el hecho de que
el orbital 4s fuera ocupado en potasio y calcio, es irrelevante para el escandio
ya que se trata de un sistema aislado diferente, con su propio conjunto de
energías orbitales [2,4].
Aunque la Figura 3 predice correctamente la evolución de las energías orbitales
en el caso de los metales de transición, no sirve para explicar por qué el orbital
4s se ocupa preferentemente a otro de menor energía en el estado
fundamental.
Para la teoría de Hartree-Fock esta situación no es una paradoja ya que los
orbitales ocupados en el estado fundamental son aquellos que hacen mínima la
energía del átomo. Es decir que el orbital 4s se ocupa antes que el 3d porque
la energía del átomo calculada resulta menor. Sin embargo esta afirmación
merece una explicación adicional ya que si 4s es mayor que 3d ¿no debería
ser la configuración electrónica de escandio en el estado fundamental, (Ar)
(3d)3?
Para responder a este interrogante es necesario puntualizar que en el modelo
de Hartree-Fock la energía orbital depende de la configuración, es decir del
conjunto particular de números de ocupación orbital [3,4], como se pone de
manifiesto al analizar las siguientes configuraciones para el escandio:
X:(Ar) (4s)2 (3d)1
Y:(Ar) (4s)1 (3d)2
Z:(Ar) (3d)3.
La energía de un electrón en 3d (3d) en la configuración X, es la energía de un
electrón moviéndose en el campo del core (Ar) y de dos electrones 4s. Es
distinta de la energía 3d en la configuración Y, que corresponde a la energía de
un electrón moviéndose en el campo del core (supuesto invariable), de un
electrón 4s y de otro electrón 3d. También es diferente de 3d en la
configuración Z.
Las diferencias en las energías orbitales se originan en las diferentes
repulsiones interelectrónicas según los orbitales ocupados. El orbital 4s es
mucho mayor y más difuso que el 3d y puede esperarse que dos electrones
distribuidos en los orbitales 3d se repelan entre sí más fuertemente que dos
electrones en 4s. Los cálculos Hartree-Fock muestran que para cualquier metal
de transición, átomo o ion, la energía de repulsión entre dos electrones según
los orbitales ocupados, en orden creciente es
Erep(4s,4s) < Erep(4s,3d) < Erep(3d,3d)
En la Figura 5 se observa que al pasar de la configuración X a la configuración
Y se elevan las energías de los orbitales 4s y 3d.
El aumento en la energía orbital es debido al incremento en las repulsiones
electrónicas. En la configuración X la energía de un electrón en un orbital 4s
(4s) incluye una repulsión con otro electrón en 4s - Erep(4s,4s) - y una
repulsión con un electrón en 3d - Erep (4s,3d) -. En la configuración Y, 4s
incluye dos repulsiones (4s,3d). Luego en la transición X  Y el aumento en 4s
se debe al reemplazo de una interacción de repulsión (4s,4s) por otra de mayor
energía (4s,3d).
El aumento de 3d en dicha transición es debido al reemplazo de una repulsión
(3d,4s) en la configuración X por una repulsión (3d,3d) de mayor energía en la
configuración Y.
Aunque no es obvio del análisis de la Figura 5 que la configuración X tiene
menor energía que la Y como muestran los cálculos Hartree-Fock, dado que la
energía total del átomo no es la suma de las energías orbitales (ecuación 1),
permite comprender por qué en el estado fundamental un orbital de mayor
energía (4s) es ocupado a pesar de existir orbitales vacantes de menor energía
(3d). El punto es que los orbitales vacantes de menor energía en el estado
fundamental, tienen energía mayor en otra configuración en la cual dichos
orbitales son ocupados. Dicho de otra manera, los orbitales considerados
vacantes sólo están disponibles a una energía mayor que la del orbital más alto
ocupado.
Resumiendo, el principio de Aufbau depende de la minimización de la energía
total del átomo y no de las energías orbitales, lo que es explicado considerando
que para un dado átomo no existe un único conjunto de energías orbitales
como sugiere la Figura 3, sino que cada configuración electrónica tiene su
propio conjunto. Esto hace evidente otra diferencia con las soluciones del
átomo de hidrógeno, en cuyo caso los niveles de energía son definidos por la
ecuación de Schrödinger, sin considerar cuál de ellos pueda estar ocupado.
Figura 4- Configuraciones electrónica externas de potasio, calcio y
escandio.
Figura 5 - Cambio de la energía orbital con la configuración electrónica.
Representación esquemática para el escandio de acuerdo a cálculos a HartreeFock.
PRINCIPIO DE EXCLUSIÓN DE PAULI
En 1925, el físico cuántico Wolfgang Pauli descubrió el «principío de
exclusíón», según el cual los electrones (que son pequeñas partículas
cargadas eléctricamente que pululan alrededor del núcleo atómico) no pueden
solaparse uno sobre otro, se excluyen mutuamente, y si se intenta presionar a
dos electrones en la misma órbita para que se unan, se repelen. Esta fuerza de
repulsión no se debe al hecho de que las cargas eléctricas correspondientes de
los electrones se repelan, sino que se trata de una fuerza de repulsión
completamente nueva, mucho más fuerte que la electromagnética. Esta nueva
fuerza, llamada «fuerza de intercambio» sólo puede comprenderse basándose
en la teoría cuántica y no existe nada análogo a ella en la física clásica. Su
existencia al nivel atómico es lo que impide que se colapsen las nubes
electrónicas que rodean los núcleos atómicos.
Si imaginamos un gas de electrones e imaginamos luego que aplicamos
una presión sobre dicho gas, la fuerza de intercambio repelente entre los
electrones individuales creará una «presión de Fermi» opuesta que, en
principio, no resistirá a la aplicada. Hay que presionar intensamente un gas
para percibir esta presión de resistencia de Fermi. Sólo actúa cuando los
electrones se acercan tanto que sus ondas asociadas comienzan a solaparse.
Uno de los ejemplos sobre esas condiciones se da en el interior de las
estrellas.
En física cuántica, el principio de
exclusión de Pauli es, para los
científicos de la especialidad, una regla
que establece que dos partículas en el
mismo estado (idéntico espín, carga de
color, momento angular, etc.) no pueden
existir en el mismo lugar y al mismo
tiempo.
Aplicando esta regla, los físicos
han logrado una importante distinción
en la categoría de las partículas:
partículas que están sujetas a la
exclusión de Pauli – los fermiones– y
partículas que no sometidas a ello –los
bosones–.
En física cuántica, la carga de
colores de las partículas no
tiene relación con los colores
de
la
luz
visible.
Se trata de un simple medio
de convertibilidad.
En resumen, se trata de un
principio que establece que dos partículas similares no pueden existir en el
mismo estado, es decir, que no pueden tener ambas la misma posición y la
misma velocidad, dentro de los límites fijados por el principio de incertidumbre.
Por otra parte, a través del principio de exclusión se puede explicar por
qué las partículas materiales no colapsan en un estado de casi extrema
densidad, bajo la influencia de las fuerzas producidas por las partículas de
espín 1, 1½ y 2 : si las partículas materiales están casi en la misma posición,
deben tener entonces velocidades diferentes, lo que significa que no estarán en
la misma posición durante mucho tiempo.
Sin la existencia del principio de exclusión, se hace difícil imaginar cuál
sería la estructura de la naturaleza. Los quarks no formarían protones y
neutrones independientes bien definidos. Ni tampoco estos formarían, junto con
los electrones, átomos independientes bien definidos. En función de nuestros
conocimientos todas las partículas se colapsarían formando una «sopa» densa,
más o menos uniforme.
Una de las más importante de esas reglas es el principio de exclusión de
Pauli: un orbital atómico determinado puede ser ocupado por sólo dos
electrones, pero con el requisito de que los espines de ambos deben ser
opuestos. Estos electrones de espines opuestos se consideran apareados.
Electrones de igual espín tienden a separarse lo máximo posible. Esta
tendencia es el más importante de los factores que determinan las formas y
propiedades de las moléculas.
Para llegar a ese principio de exclusión, Pauli, previamente descubrió
otro, «el principio de antisimetría», el cual señala: La función de onda
total de un conjunto de electrones (fermiones), debe ser antisimétrica con
respecto al intercambio de cualquier par de electrones.
Ahora bien, si existe una parte espacial simétrica, la parte de espín debe
ser antisimétrica y viceversa. Ello permite poder construir la función del estado
fundamental y del estado excitado, cuya energía es conocida al igual que su
parte espacial.
 Estado fundamental:
[01]
 Estado excitado de menor energía :
[02]
 Estado excitado de mayor energía :
[03]
Este principio de antisimetría derivó a Pauli al principio de exclusión, en
el cual no pueden existir en un sistema, como lo hemos mencionado ya, dos
electrones con el mismo conjunto de números cuánticos. Es decir que tengan la
misma parte espacial y de espín., ya que si se tiene:
,
o sea, una función simétrica con respecto al intercambio del electrón 1 por el 2.
Pero se deriva otra consecuencia y es aquella en que el número de
electrones que pueden tener la misma parte espacial, es decir que están
definidos por un orbital que se caracteriza por sus números cuánticos ,, m,
es como máximo de dos, y además si hay dos, estos deben tener espines
opuestos.
Antes de continuar, recordemos que, según el principio de exclusión de
Pauli, dos fermiones no pueden estar en el mismo estado. En este respecto se
distinguen radicalmente de los bosones, los cuales sí pueden ocupar todos el
mismo estado. Este hecho juega un papel decisivo en la explicación de las
propiedades de los sistemas compuestos de fermiones, tales como los átomos
(sistema de electrones) o los núcleos (sistema de protones y neutrones).
También es la razón por la que sistemas de bosones como el campo
electromagnético pueden contener cantidades tan enormes de elementos
(fotones) que aparecen como clásicos en situaciones ordinarias.
El átomo es un sistema compuesto de un núcleo con una carga positiva
Ze y N electrones con carga negativa –e cada uno. Es neutro cuando Z = N e
ionizado cuando N < Z y posee una carga positiva (Z – N)e. Como el núcleo es
mucho más pesado que el electrón, es una aproximación muy buena
despreciar su movimiento y, al colocarlo en el origen, reducir su efecto al
campo central electrostático de Coulomb. Así, el hamiltoniano para el átomo
toma la siguiente forma:
[04]
En esto, lo medular es que lo que determina la estructura del átomo es el
principio de Pauli, o sea, la exigencia de antisimetría de la función de onda de
los electrones, que tienen espín ½ y son fermiones. Es importante tener en
cuenta que debido a la existencia del espín, la función de onda además de las
coordenadas también depende de las variables del espín n para cada
electrón, aunque el hamiltoniano [04] no dependa de ellas.
La interacción total en [04] se separa en dos partes: la de los electrones
con el núcleo y la de los electrones entre sí. Con una carga Ze lo bastante
grande, la interacción con el núcleo constituye la parte dominante. Por lo tanto,
para tener una idea cualitativa de la estructura del átomo, se puede prescindir
de la repulsión de los electrones entre sí, como una primera aproximación. La
imagen que resulta no es exacta, pero conserva las características más
significativas de los átomos reales. Sin interacción mutua entre los electrones el
hamiltoniano 04] se reduce a una suma de partes independientes:
[05]
donde
[06]
es el hamiltoniano del átomo de hidrógeno para el electrón número i. Así se
hace posible la solución explícita de la ecuación de Sclirödinger para el átomo
completo.
La presencia del principio de exclusión de Pauli es una de las
características que hacen posible la distinción entre lo que consideramos como
materia – aire, ladrillos, llamas , y así sucesivamente – con respecto a los
fotones o gravitones . La materia está hecha por los fermiones,
predominantemente protones, neutrones, y electrones, los cuales obedecen al
principio de la exclusión de Pauli. Por otra parte, los fotones y los gravitones
son bosones, y no obedecen a ese principio de exclusión; consecuentemente,
su comportamiento es muy disímil al de la materia, aunque las reglas básicas
de la mecánica quántica se aplican a ambos tipos de partículas.
El fenómeno del revestimiento de la estructura del electrón de un átomo
se debe al principio de exclusión de Pauli. Un átomo eléctricamente neutro
contiene en el núcleo una cantidad de electrones articulados (bounds) igual al
número de protones. Puesto que los electrones son fermiones, el principio de
exclusión de Pauli les prohíbe ocupar el mismo estado cuántico.
Por ejemplo, consideremos un átomo neutro de helio con dos electrones
articulados. Ambos electrones pueden ocupar el estado más bajo de la energía
(E1), pero siempre que sus espines sean disímiles. Ello no viola el principio de
exclusión de Pauli por que los espines son parte del estado cuántico del
electrón, ya que ambos electrones están ocupando diferentes estados
cuánticos. Por otra parte, un átomo neutro de litio tiene tres electrones
articulados. Dos esos electrones pueden ocupar el estado E1, pero el tercero
tiene que ocupar un estado de mayor energía (E2). De manera semejante
ocurre con los elementos sucesivos que van produciendo revestimientos cada
vez de mayor energía. Las características químicas de un elemento dependen
en gran parte del número de electrones de su revestimiento exterior, lo que da
lugar también a su posición en la tabla periódica.
El principio de Pauli es también gran responsable de la estabilidad de la
materia. Las moléculas no se pueden empujar una cerca de otra
arbitrariamente, porque los electrones articulados de cada molécula no pueden
ser incorporados en otra en el mismo estado que tenían previamente, debido al
efecto de repulsión de Lennard-Jones.
1.1.10.- Configuraciones electrónicas: Regla de Hund.
Los electrones se distribuyen en los orbitales de tal manera que resulta el mayor número
de electrones no apareados; es decir, en los orbitales del mismo tipo, primero se llenarán
todos con un solo electrón, y después entrarán los siguientes electrones con spin
contrario.
Configuración electrónica 9x 1S2 2p5
Diagrama de orbitales
1S
2S
Electrón Diferencial.
Es el último electrón de la configuración electrónica, el cual diferencia a un elemento
del elemento precedente.
Regla de Hund
El orden de llenado en un orbital es aquel en el que
hay más orbitales semiocupados. En otras palabras, al
llenarse orbitales de igual energía(los tres orbitales p,
los cinco d o los siete f), los electrones se distribuyen
lo
más desapareados posible(con sus spines paralelos).
El átomo es más estable cuando tiene e- desapareados.
Llenado de orbitales d
Sc: [Ar] 4s2 3d1
Ti: 4s2 3d2
V : 4s2 3d3
Cr: 4s1 3d5 (*)
Mn: 4s2 3d5
Fe: 4s2 3d6
Co: 4s2 3d7
Ni: 4s2 3d8
Cu: 4s1 3d10 (*)
Zn: 4s2 3d10
Llenado de orbitales f
Elementos de transición interna: Lantánidos y actínidos.
Loslantánidos comienzan con el lantano, cuya configuración
electrónica es igual que la de un metal de transición, se
coloca debajo del Sc(escandio) y del Y(itrio).
La: [Xe]6s25d1
Los lantánidos colocan su último electrón en un orbital
4f.
Ac: [Rn]7s26d1
Los Actínidos colocan su último electrón en un nivel 5f
En general el llenado de orbitales ha de tener en
cuenta que las configuraciones que contienen subniveles
completos o que contienen la mitad de los electrones que
puedan contener,( Cr, Cu)son más estables.
La configuración electrónica de los iones viene
determinada por las fuerzas entre los electrones y las
variaciones de la carga nuclear.
Al formarse un ión + se pierden en primer lugar los
electrones de los niveles más externos pertenecientes a los
orbitales p, después los s y por último los de los
orbitales
d del nivel anterior.
Los elementos de la primera serie de transición
comienzan perdiendo los electrones del orbital 4s.
Lo que determina la estabilidad de una configuración
electrónica es el efecto neto de: atracción núcleoelectrón,
protección de un electrón por otros, repulsiones
interelectrónicas.
Propidades periódicas
a)Radio atómico
Es una medida del tamaño del átomo, aunque no se puede
precisar con detalle el tamaño, ya que la nube electrónica
que rodea al núcleo no tiene una superficie bien
delimitada.
Se considera el radio del átomo, como la mitad de la
distancia que existe entre los centros de dos o más átomos
que estén en contacto.
1.2.- Periodicidad Química.
1.2.1.- Desarrollo de la tabla periódica moderna.
Características de la Clasificación Periódica Moderna de los Elementos.
Se han hechos diversas modificaciones a la tabla periódica desde los tiempos de
Mendeleev. Entre las más importantes debe de mencionarse la ordenación de los
elementos de acuerdo con el incremento del número atómico, en lugar del peso atómico
y la estructuración de conjuntos de elementos (bloques) relacionados con las
configuraciones electrónicas y en el modelo cuántica del átomo.
Por lo general, la tabla periódica cuántica incluye: símbolo del elemento, número
atómico, masa atómica, valores de los números cuánticos (n, l. m y s), clase, período,
familia, número de electrones en los subniveles y los orbitales que contienen uno o dos
electrones.
Estructura
En la tabla cuántica los elementos se clasifican en orden creciente de sus números
atómicos y en función de sus configuraciones electrónicas.
Los elementos se encuentran agrupados en cuatro clases según la posición de su
electrón diferencial: el bloque s, el p, el d y el f, que contienen elementos con electrón
diferencial localizado en orbital s, p, d o f, respectivamente. La clase se indica en la
parte inferior de los conjuntos.
Los elementos se encuentran también en en tres tipos que se indican en la parte inferior
de las clases:
Elementos representativos. Aquéllos con electrón diferencial en orbital de subnivel s o
p.
Elementos de transición con electrón diferencial en orbital de subnivel d.
Elementos tierras raras o lantánidos o actínidos con electrón diferencial en f.
La tabla periódica cuántica está integrada por ocho períodos, cuyo valor se indica en la
columna de la extrema izquierda de la tabla.
Período
Número de elementos
1o
2
2o
2
3o
8
4o
8
5o
18
6o
18
7o
32
8o
Está incompleto pero
Cuando se llena tendrá 32
Período es un conjunto de elementos que tienen el mismo valor de la suma n + 1 (ene +
ele = contenido de energía), para su último electrón (electrón diferencial).
Por ejemplo, el período 4o está integrado por los elementos Al, Si, P, S, Cl, Ar, K y Ca,
todos ellos tienen el mismo valor de la suma n + 1 para su electrón diferencial, que en
este caso es igual a cuatro.
Elemento
Al
Si
P
S
Cl
Ar
K
Ca
Electrón
diferencial
3p
3p
3p
3p
3p
3p
4s
4s
En n + 1
3+1
3+1
3+1
3+1
3+1
3+1
4+0
4+0
Suma
4
4
4
4
4
4
4
4
La clasificación periódica cuántica consta de 32 familias cuyo valor aparece en la parte
inferior de las columnas. Existen 32 familias debido a que hay dos electrones en s, seis
en p, diez en d y catorce en f.
Familia es un conjunto de elementos que tienen el mismo número de electrones en el
nivel donde se encuentra colocado en electrón diferencial.
1.2.2.- Clasificación periódica de los elementos.
Después de conocer diferentes clasificaciones que existen sobre las
distintas sustancias, resulta de gran interés y de singular importancia para una
buena NOMENCLATURA de los compuestos, el conocer ciertas características
de los elementos de acuerdo al acomodo que guardan en la TABLA
PERIODICA. El ordenamiento de los elementos en la tabla periódica no fue
hecho al azar, sino más bien es el fruto de un gran número de intentos por
agruparlos en función de sus propiedades y el orden seguido es en base a un
NUMERO ATOMICO que viene siendo la cantidad de protones existentes en el
NUCLEO del átomo.
Tal vez la tabla periódica que resulte más común , en esta podemos apreciar 7
renglones horizontales llamados PERIODOS, además de 18 columnas
verticales llamadas GRUPOS.
El nombre de TABLA PERIODICA la recibe precisamente porque cada cierto
número de elementos las propiedades químicas se repiten; quedando
colocados uno bajo el otro todos aquellos elementos que presentan
propiedades con similitud para formarse así un GRUPO.
Los PERIODOS están formados por un conjunto de elementos que teniendo
propiedades químicas diferentes, mantienen en común el presentar igual
número de niveles con electrones en su envoltura, correspondiendo el número
de PERIODO al total de niveles.
Las propiedades químicas de los elementos dependen de la distribución
electrónica en los diferentes niveles, por ello; todos aquellos que tienen igual
número de electrones en su último nivel presentan propiedades químicas
similares, correspondiendo el número de período en que se encuentra ubicado,
al del último nivel con electrones y el número de grupo guarda relación con la
cantidad de electrones en la última capa.
La tabla periódica puele dividirse en diversas formas según las propiedades
que se deseen estudiar, de tal suerte que se agrupan conjuntos de elementos
con características comunes.
METALES, NO METALES Y METALOIDES
Aún antes de establecerse la tabla periódica; ya el creador de la SIMBOLOGIA
de los elementos J. J. BERZELIUS publicó en 1814 una clasificación
sistemática en donde agrupaba dos tipos: los METALES y los NO METALES.
Las características de los elementos METALICOS son:





Conducen con facilidad el calor y la electricidad.
Presentan brillo metálico
Generalmente pueden ser laminados o estirados formando alambres,
propiedades que se conocen como MALEABILIDAD y DUCTILIDAD.
Por lo regular a temperatura ambiente son sólidos excepto Hg, Ga, Cs y
Fr.
Al combinarse con NO METALES ceden electrones por lo que adquieren
cargas positivas (CATIONES).
Los NO METALES presentan las siguientes características:



Son malos conductores del calor y la electricidad.
No son maleables ni dúctiles.
Reciben electrones al combinarse con los METALES adquiriendo así
cargas NEGATIVAS (ANIONES).
Algunos elementos suelen comportarse según las condiciones como metales o
como no metales; a estos se les conoce como METALOIDES.
En la clasificación periódica de DIECIOCHO columnas podemos apreciar a
estos grupos de elementos claramente delimitados, lo cual nos parece
razonable si pensamos que las características de ellos dependen de la
distribución electrónica, entre más próximos estén los elementos, mayor
semejanza tendrán en sus propiedades y esto se debe a que la distribución
electrónica presenta también una gran semejanza.
Si admitimos que las propiedades químicas de los elementos dependen de la
ubicación de los electrones en su envoltura, tenemos una CLASIFICACION DE
ELEMENTOS EN FUNCION DE SU DISTRIBUCION ELECTRONICA. En esta
clasificación los elementos se agruparon en cuatro bloques según el tipo de
orbital atómico en que se ubique su electrón diferencial.
Otra clasificación que resulta importante conocer y es de gran utilidad en la
NOMENCLATURA es la que nos brinda información sobre la capacidad de
combinación de los elementos o sea su VALENCIA así como su ESTADO o
NUMERO DE OXIDACION.
Existe una clasificación que ubica a los elementos representativos en ocho
grupos identificados como A y a los de transición en B. Los elementos
representativos son conocidos así porque el número de grupos representa la
cantidad de electrones en su CAPA DE VALENCIA o sea el ULTIMO NIVEL y
la cantidad de electrones en esa capa nos indica la valencia máxima que el
elemento puede presentar. La VALENCIA de un elemento se refiere a la
capacidad de combinación que presenta; en el caso de los NO METALES se
relaciona con el número de átomos de hidrógeno con que se puede enlazar y
en los METALES con cuántos átomos de cloro se une.
Ejemplos: El Calcio se puede unir a dos átomos de Cloro por lo que su valencia
es dos. CaCl2
El Oxígeno forma agua uniéndose a dos hidrógenos, su valencia también será
dos. H2O
El Nitrógeno se une a tres Hidrógenos en la formación de Amoníaco,su
valencia es tres. NH3
1.2.3.- Propiedades atómicas y variaciones periódicas: carga nuclear efectiva,
radio atómico, radio iónico, energía de ionización, afinidad electrónica,
electronegatividad.
La carga nuclear efectiva, es la fuerza con la cual el núcleo positivo atrae a los
electrones de la capa de valencia. Está en función inversa a la distancia de los electrones
y en razón directa al número de protones. Por lo tanto, a mayor radio atómico menor
carga nuclear, y a menor radio atómico mayor atracción:
1.2.3.1. Variación de la carga nuclear en grupos y periodos de la tabla.
Para los elementos de un grupo de la tabla, la carga nuclear disminuye de arriba
hacia abajo y aumenta a largo de un período de izquierda a derecha.
Tamaño Atómico.
Con frecuencia pensamos que los átomos son objetos esféricos con límites bien
definidos. Sin embargo, una conclusión que podemos obtener de la mecánica cuántica,
es que el átomo no tiene límites claramente definidos que determinen su tamaño.
La forma en el que un átomo reacciona químicamente depende de muchos factores,
entre los que podemos mencionar la carga nuclear, el tamaño efectivo del átomo, la
configuración electrónica, etc.
La carga nuclear de un átomo aumenta al aumentar el número atómico, debido a que el
número de protones se incrementa; sin embargo, los electrones de valencia se
encuentran protegidos de la acción del núcleo por los electrones de los niveles interiores
que se encuentran más cerca de este.
La carga nuclear efectiva que siente un electrón exterior (electrón de valencia) es la
parte de la carga del núcleo que influye sobre él. La carga nuclear efectiva no es igual a
la carga núcleo, porque los electrones de los niveles interiores contrarrestan (efecto
pantalla) o protegen parte de la carga del núcleo.
En 1870, Lothar Meyer fue el primero en observar la variación periódica del tamaño de
los átomos y calculó el volumen atómico de los elementos dividiendo el peso atómico
entre la densidad. El volumen atómico calculado de esta manera es únicamente una
indicación cualitativa del tamaño del átomo, porque la densidad de un elemento
depende de su temperatura y su estructura cristalina. Aquellos elementos que presentan
diferentes formas cristalinas alotrópicas tendrán, evidentemente, más de un volumen
átomico. Sin embargo, el tamaño atómico es un concepto muy útil que nos puede
ayudar a comprender el comportamiento químico de los elementos
Energía de Ionización.
La energía de ionización, también llamada potencial de ionización, es la energía que
requiere un átomo gaseoso en estado basal para perder totalmente un electrón.
La energía de ionización aumenta para los elementos de un período de izquierda a
derecha y disminuye para los elementos de un grupo de arriba hacia abajo. Lo anterior
se origina por interrelación entre el efecto patalla, el tamaño del átomo y la carga del
núcleo:
1.2.3.2. Variación del potencial de ionización en grupos y períodos de la tabla
periodica.
Afinidad Electrónica.
L a afinidad electrónica es la cantidad de energía que se desprende o absorbe por la
adición de un electrón al átomo neutro gaseoso de un elemento, para producir un ión
negativo.
En general, la afinidad electrónica es mayor para los no-metales que para los metales.
Esta medida de la facilidad con que los elementos captan electrones, es consecuencia de
la configuración electrónica, siendo mucho mayor para los elementos situados cerca de
los gases nobles.
1.2.3.4. Elementos de mayor afinidad electrónica en la tabla periodica.
Número de Oxidación.
Número de oxidación o estado de oxidación, es el número de electrones que gana o
pierde un elemento cuando se combina para adquirir la configuración de un gas noble
inmediato.
Debido a la gran inactividad química de los gases nobles, se considera que su
configuración electrónica es estable y tiende a ser adoptada por los demás elementos
cuando entra en reacción. Los gases nobles poseen ocho electrones de valencia
acomodados en ns2np6, con excepción del helio que sólo tiene dos colocados en 1s.
Cuando un átomo neutro se combina puede perder electrones y adquiere un número de
oxidación positivo, tantas veces positivos como electrones haya perdido, o puede ganar
electrones adquiriendo un número de oxidación negativo cuyo valor es igual al número
de electrones ganados.
Los elementos de los grupos I A, II A y III A, que tienen 1, 2 y 3 electrones de valencia
respectivamente, cuando se combinan tienden a perderlos para adquirir la configuración
electrónica del gas noble inmediato. Los miembros de la familia I A presentan número
de oxidación 1+, los de la II A el de 2+ y el grupo III A el estado de oxidación 3+.
Los elementos del grupo IV A pueden perder o ganar electrones; sin embargo,
generalmente comparten electrones con otros átomos. Los números de oxidación
característicos son 4+ ó 4-.
En los grupos V A, VI A y VII A existe una tendencia general a ganar electrones para
adquirir la configuración electrónica del gas noble inmediato. Estos elementos muestran
número de oxidación de 3- la quinta familia, 2- la sexta y 1- la séptima. Estos
elementos, excepto el flúor y el oxígeno, por ser los más electronegativos, pueden
perder electrones y tener números de oxidación positivos. La tendencia a perder
electrones y tener números de oxidación positivos.
Los metales exhiben siempre números de oxidación positivos y los no metales al unirse
a metales tienen números de oxidación negativos, pero cuando se unen a no metales más
electronegativos como el flúor o el oxígeno, actúan con estados de oxidación positivos.
Todos los elementos en estado negativo o molecular (Cl2 , H2 , O2, Fe, P4, Na) tienen
número de oxidación de cero.
Los gases nobles por tener una configuración estable, presentan número de oxidación de
cero. El elemento flúor por ser el más electronegativo tiene estados de oxidación de 1- y
cero. El oxígeno por seguir en electronegatividad tiene 2-, cero y 1- en los peróxidos. El
hidrógeno presenta número de oxidación de 1+, cero y 1-.
Electronegatividad.
La electronegatividad, es una medida relativa del poder de atracción de electrones que
tiene un átomo cuando forma parte de un enlace químico. Su unidad es el pauling ya
que fue Linus C. Pauling quien estableció esta escala. En un grupo la electronegatividad
disminuyede arriba hacia abajo y en un período aumenta de izquierda a derecha.Así, el
elemento más electronegativo es el flúor (4.0), le sigue el oxígeno (3.5), luego el cloro
(3.0), etcétera.
1.2.3.5. Variación de Electronegatividades en Grupos y Período de la
tabla periódica.
Con base en lo anterior, debemos considerar que los elementos (no metales) localizados
en la esquina derecha superior de la tabla periódica son los que tienden a ganar
electrones con mayor facilidad; por lo tanto, no son buenos conductores de la
electricidad, se reducen fácilmente y se usan comúnmente como oxidantes.
1.2.3.6. Elementos de Mayor Electronegatividad en la Tabla Periódica
1.3.- Elementos de importancia económica, industrial y ambiental en la región o
en el país.
Comúnmente se agrupan los elementos en Metales y No-Metales.
Los metales son elementos que tienen generalmente brillo metálico, son
maleables, dúctiles, buenos conductores del calor y de la electricidad; la propiedad
fundamental que justifica la clasificación, es que sus óxidos al combinarse con el agua
forman hidróxidos.
Los no-metales son elementos químicos que con el oxígeno forman óxidos, que
se combinan con el agua para constituir ácidos; estos óxidos se conocen con el nombre
de anhídridos.
La tabla periódica nos muestra que los elementos están agrupados de modo tal
que parece indicar su distribución en la naturaleza.
En la parte superior están los gases que constituyen la atmósfera como en
nitrógeno y el oxígeno. En el centro están las sales y el agua, si se toma en cuenta que
los extremos de la tabla se cierran y se unen los metales alcalinos con los halógenos.
En la parte inferior están los metales que en forma de minerales se encuentran en
el interior de la tierra.
Elementos Importantes:
Aluminio.
El aluminio es un metal de un brillo semejante al de la plata, y se deja pulir
fácilmente. Generalmente la superficie está cubierta de una capa opaca que está formada
de óxido. Es el metal má ligero de los comunes, y transporta fácilmente la electricidad.
Es un agente reductor muy poderoso, por lo que se usa para obtener el cromo y el
manganeso.
Usos:
El aluminio no es atacado por los alimentos comunes, por esta razón y por ser un
conductor del calor, se está usando actualmente en la fabricación de utensilios de
cocina. El polvo de aluminio tiene una gran aplicación en la fabricación de pinturas,
principalmente para cubrir los objetos de fierro que están en la intemperie. También se
inicia el uso del aluminio como conductor de la corriente eléctrica, porque su
conductibilidad es muy cercana a la del cobre, con la gran ventaja de su densidad baja.
En forma de aleaciones se emplea en la construcción de los aeroplanos; entre la
aleaciones que tiene mayor aplicación está el duraluminio, aleación formada con
aluminio, cobre y manganeso tan duro como el acero y cuya densidad es la mitad del
mismo; el magnalium, el cual conserva la ligereza del aluminio y se deja elaborar con
facilidad. En la actualidad el papel aluminio o lámina delgada está sustituyendo al
estaño, pues se emplea en la envoltura, de muchos artículos.
Azufre.
El azufre es elemento no metal, sólido de color amarillo, más familiar y fue uno
de los primeros que llamó la atención del hombre, por encontrarse junto con las rocas
volcánicas en la superficie de la tierra.
El azufre se encuentra nativo y combinado en la tierra; en forma combinada se
halla en los sulfuros y en los sulfatos. En México existe al estado nativo en el cráter del
Popocatépetl de donde se explotó en una época en gran escala.
Uso:
El azufre se usa en la fabricación del papel a partir de la madera; en la industria
del petróleo para la refinación de la gasolina; en la vulcanización del caucho y en gran
variedad de productos químicos entre los que debemos mencionar en primer lugar el
ácido sulfúrico, producto básico de grandes industrias, el dióxido de azufre en la
industria del blanqueo, de los sulfitos, sulfatos y poli sulfatos.
Cobalto.
Metal de color blanco que se emplea en la elaboración de aceros especiales
debido a su alta resistencia al calor, corrosión y fricción. Se han encontrado minerales
oxidados y sulfuros en Sonora, Jalisco, Michoacán, Puebla y Oaxaca.
Uso:
Se emplea en herramientas mecánicas de alta velocidad, imanes y motores. En
forma de polvo se emplea como pigmento azul para vidrio. Es catalizador. Su isótopo
radiactivo se emplea en el I.N.I.N. México, porque produce radiaciones gamma.
Hierro.
El hierro es un metal de color blanco-grisáceo muy dúctil y maleable. Cuando se
le coloca en un campo magnético adquiere la propiedad de atraer los cuerpos
magnéticos. El oxígeno del aire en presencia húmeda se combina con él, produciendo el
hidrato férrico llamado herrumbre. Cuando se le cubre con una capa de zinc se le
conoce como fierro galvanizado y cubierto con el estaño forma la hojalata. En sus
combinaciones con los demás elementos se le encuentra unido con dos valencias
positivas y con tres; en el primer caso las sales llevan el nombre de ferrosas y en el
segundo el de férricas.
Uso:
Se le emplea en la industria, arte y medicina. Para fabricar acero, cemento,
fundiciones de metales no ferrosos; la sangre lo contiene en la hemoglobina.
Flúor.
El flúor es el elemento electronegativo más activo de todos los conocidos;
debido a su actividad química intensa no se encuentra libre en la naturaleza, sino en
forma de compuestos naturales o minerales, entre los que debemos recordar la fluorita
(CaF2) y la criolita (NaAlF6); Ambos minerales son muy usados, el primero para la
preparación del ácido fluorhídrico y el segundo para la obtención del aluminio.
Uso:
Con el flúor se obtienen ciertos compuestos orgánicos halogenados como el
teflón, nombre comercial del politetrafluoretileno, este compuesto es un plástico muy
resistente a las temperaturas elevadas, a los ácidos y a la acción de los disolventes, se
emplea para recubrir: sartenes, tuberías, aviones, etc.
Fósforo.
El fósforo (palabra de origen griego que significa "llevo luz"), elemento no
metálico, que por su gran actividad química no se encuentra libre en la naturaleza, sino
que abunda en forma de minerales. Los huesos y los dientes encierran alrededor de 50
% de fosfato de calcio. Muchos terrenos contienen pequeñas cantidades de fosfatos
solubles que son necesarias para el desarrollo de las plantas.
Uso:
Es la materia prima en la fabricación de las cerillas, bajo la forma de fósforo rojo
o en la de bisulfuro de fósforo (P4S3). Tiene aplicaciones para la elaboración de
detergentes, plásticos, lacas, explosivos, refinación de azúcar, industria textil, fotografía,
fertilizantes, cerámicas, pinturas, alimentos para ganados y aves.
Mercurio.
Se encuentra nativo en la naturaleza, metal líquido a temperatura ambiente de
color blanco brillante, resistente a la corrosión y buen conductor eléctrico.
Uso:
Se le emplea en la fabricación de instrumentos de precisión, baterías,
termómetros, barómetros, amalgamas dentales, armas para preparar cloro, sosa cáustica,
medicamentos insecticidas, fungicidas y bactericidas.
Plata.
La plata es un metal blanco, no es duro. Se encuentra en forma nativa,
generalmente en las rocas cuarzosas, pero en pequeñas cantidades. Es el mejor
conductor del calor y de la electricidad.
Uso:
Su uso tradicional ha sido en la acuñación de monedas y manufactura de vajillas
y joyas. Se emplea en fotografías, aparatos eléctricos, aleaciones, soldadura. La
producción de plata en México se obtiene como subproducto del beneficio de sulfuros
de plomo, cobre y zinc que la contienen. Recientemente se ha substituido su uso en
monedas por la aleación cobre-níquel.
Plomo.
El plomo es un metal blando y muy pesado, de bajo punto de fusión, bajo límite
elástico, resistente a la corrosión, se le obtiene del sulfuro llamado galena PbS.
Uso:
El plomo se usa en la manufactura de acumuladores; en la fabricación de metales
para chumaceras; en la copelación de la plata, en la fabricación de tubos y de
soldaduras, en la elaboración de tipos de imprenta, en la fabricación del litargirio y del
minio.
Oro.
Es seguramente este metal el más antiguamente conocido por el hombre. El oro
es un metal amarillo, relativamente blando que funde a más de 1000 oC, es el metal más
maleable y dúctil de los conocidos. Al estado puro es blando, para su uso de joyería y en
monedas, se hace una aleación con el cobre. Las monedas de oro de todas las naciones
tienen la misma ley: 90 de oro en 100 de aleación. Las aleaciones de oro se expresan en
quilates, el oro puro es de 24 quilates.
Usos:
El oro se emplea en gran escala para la acuñación de monedas y para la
fabricación de joyas. En odontología se usa porque es un metal inalterable, es atacado
únicamente por el agua regia.
Las sales de oro se emplea para el dorado electrolítico y para el virado
fotográfico
Uranio.
Utilizado como combustible nuclear, éste es un elemento raro en la naturaleza y
nunca se presenta en estado libre. Existen 150 minerales que lo contienen. El torio se
encuentra asociado al uranio. En México este mineral está regido por la ley promulgada
en 1949, que declara como reservas mineras nacionales los yacimientos de uranio y
torio y demás substancias de las cuales se obtengan isótopos que pueden producir
energía nuclear.
Elementos de importancia económica, excluyendo a los metales. Elementos
contaminantes.
Antimonio.
El antimonio se emplea en aleaciones, metal de imprenta, baterías, cerámica y
textiles.
El envenenamiento se produce por ingestión, inhalación de vapores y
principalmente por un gas llamado estibina.
Arsénico.
Se emplea en venenos para hormigas,insecticidas, pinturas, medicamentos y
vidrio.
Es uno de los elementos más venenosos que hay, así como sus compuestos,
todos sin excepción.
Azufre.
Principalmente sus óxidos SO2 Y SO3 contaminan el aire y con agua producen
la lluvia ácida. Substancias tales como derivados clorados de azufre, sulfatos, ácidos,
son corrosivos. El gas H2S es sumamente tóxico y contaminan el aire. El azufre es
empleado en algunos medicamentos para la piel.
Bromo.
Sus vapores contaminan el aire, además sus compuestos derivados son
lacrimógenos y venenosos.
Cadmio.
Metal tóxico que se origina en la refinación del zinc; también proviene de
operaciones de eelctrodeposición y por tanto contamina agua y aire. Contenido en
algunos fertilizantes y contamina el suelo.
Cloro.
Sus vapores contaminan el aire y son corrosivos. Se le emplea en forma de
cloratos para blanquear la ropa, para lavados bucales, para cerillos. Los cloratos son
solubles en agua y la contaminan además de formar mezclas explosivas con compuestos
orgánicos.
Cromo.
El cromo y sus compuestos son perjudiciales al organismo, pues destruyen todas
las células. Se le emplea en síntesis orgánicas y en la industria del acero. Un cromato
soluble contamina el agua.
Fósforo.
El fósforo blanco o amarillo es muy venenoso.
El fósforo rojo no lo es, pero se encuentra contaminado por el blanco. Se emplea
fósforo en síntesis, pinturas, fertilizantes, plaguicidas, ocasionando contaminación de
aire, suelo y agua.
El gas PH3 es muy venenoso y los vapores de compuestos orgánicos fosforados
contaminan el aire.
Manganeso.
Se emplea en la manufactura del acero y de pilas secas. La inhalación de polvos
y humos conteniendo manganeso causa envenenamiento. También contamina el agua y
atrofia el cerebro.
Mercurio.
Metal de gran utilidad por ser líquido, pero contamina el agua, aire y causa
envenenamiento. Las algas lo absorben, luego los peces y finalmente el hombre. Los
granos lo retienen y finalmente el hombre los come.
Plomo.
El plomo se acumula en el cuerpo conforme se inhala del aire o se ingiere con
los alimentos y el agua. La mayor parte del plomo que contamina el aire proviene de las
gasolinas para automoviles, pues se requiere para proporcionarle propiedades
antidetonantes. También se le emplea en pinturas, como metal de imprenta, soldaduras y
acumuladores. Por su uso el organismo se ve afectado de saturnismo. Sus sales son
venenosas como el acetato.
UNIDAD 2.- ENLACES QUÍMICOS Y EL ESTADO SÓLIDO (CRISTALINO).
2.1.- INTRODUCCIÓN.
2.1.1.- Conceptos de Enlace Químico.
El estudio de varias moléculas de un mismo compuesto muestra que cada átomo se
encuentra colocado en la misma posición y distancia en relación con los demás, debido
a la formación de un ligamento entre los átomos que se conoce como enlace químico.
Los enlaces químicos son la fuerza que mantienen unidos a los átomos para formar
moléculas y cristales. Los estados de agregación de la materia, sólido, líquido y
gaseoso, dependen de estas fuerzas de enlace y éstas también determinan la forma física
de las moléculas, es decir, que sean esféricas o planas, rígidas o flexibles.
Durante el proceso de formación de un enlace se libera energía que es necesario agregar
cuando se quiere romper el enlace. La cantidad de energía necesaria para separar los
átomos de un enlace se llama energía de enlace.
2.1.2.- Clasificación de los Enlaces Químicos.
Los cambios electrónicos producen distintos tipos de fuerzas de unión o enlaces: los
interatómicos, que mantienen unidos a los átomos dentro de una molécula, como iónico
(NaCl, CaCO3), covalente (H2, O2, H2O, NH3) y metálico (Fe, Na, Al), y los
intermoleculares, que mantienen unidas a las moléculas entre átomos de ellas como
puente de hidrógeno, fuerzas de dispersión, interacciones dipolo-dipolo y son los que
explican las propiedades físicas de los compuestos, etcétera.
El enlace iónico o electrovalente se debe a la fuerza de atracción entre iones positivos y
negativos que se forman por transferencia de electrones entre átomos con una diferencia
de electronegatividad elevada.
El enlace covalente es la unión de dos átomos de no metales de electronegatividades
iguales o ligeramente diferentes, por medio de un par de electrones que ambos
comparten y suministran. Cuando las electronegatividades de los átomos son iguales, se
produce un enlace covalente no polar o apolar y el par de electrones compartido se
encuentra equidistante de los núcleos, pero cuando la electronegatividad es diferente el
par electrónico se encuentra más cerca del núcleo del átomo son iguales, se encuentra
equidistante de los núcleos.
Algunas substancias formadas por moléculas independientes se encuentran al estado
líquido y sólido, lo que indica que deben existir fuerzas de atracción entre las moléculas.
El enlace o puente de hidrógeno es la unión de dos átomos electronegativos por medio
de un hidrógeno que sirve de puente entre ambos, unidos a uno covalentemente y a otro
por fuerzas electrostáticas. Las fuerzas dipolo-dipolo se presentan en moléculas polares
que se atraen entre sí, porque el polo positivo de una queda cercano al negativo de otra.
El hecho de que moléculas no polares, donde no existen dipolos, pueden licuarse, este
hecho hace pensar en la existencia de las llamadas fuerzas de dispersión que se originan
por el movimiento electrónico que por un instante genera un dipolo, distribuyendo la
nube electrónica más de un lado que del otro y en el instante siguiente cambian las
posiciones de los polos.
Las propiedades y el comportamiento de las moléculas están íntimamente relacionadas
con la distribución que ocupan en el espacio los átomos dentro de ellas. De acuerdo con
la geometría molecular, la forma de las moléculas puede ser: lineal, angular, trigonal,
piramidal, etcétera.
Las propiedades de una substancia dependen de la naturaleza de sus unidades
estructurales y del enlace entre ellas, y se consideran cuatro tipos: compuestos iónicos,
compuestos moleculares, substancias macromoleculares y metales.
El enlace químico también depende de la energía contenida en cada uno de ellos y de la
posibilidad de un choque, colisión o encuentro con otros átomos cercanos a sus orbitales
incompletos y principalmente a los de la configuración electrónica externa.
Varios factores influyen en el tipo de enlace:
1. Energía de ionización.
2. Afinidad electrónica.
3. Actividad electrónica.
4. Radio atómico.
Al formar el enlace, los átomos ganan, pierden o comparten electrones tratando de
completar ocho electrones en su configuración electrónica externa, para ser estables
como lo son los gases raros o nobles de la octava familia.
2.2.- Símbolo de Lewis y Regla del Octeto.
Regla del Octeto; Símbolos Electrónicos de Lewis
Walter Kossel expuso la idea de que los átomos, al efectuarse las reacciones químicas,
tienden a adoptar la configuración electrónica de los gases raros o nobles, que tienen
ocho electrones en su configuración electrónica externa.
Después se aceptó la regla del octeto en la mecánica cuántica, localizada en los
subniveles periféricos ns2, np6 , los cuales suman ocho electrones y la configuración
electrónica de dichos gases es de ocho electrones, excepto en el helio que es 2He = 1s2.
Lewis y Lagmyur estudiaron la regla del octeto y la emplearon para formar compuestos
iónicos y no iónicos; así llegaron a la conclusión de que la regla del octeto no implica
que siempre haya transferencia de electrones.
En 1923, Lewis estableció que, al combinarse dos átomos pueden cumplir la regla del
octeto, no sólo por transferencia de electrones de un átomo a otro sino también por
parejas de electrones.
Lewis usó la simbología de puntitos o circulitos para representar las estructuras
atómicas. Es una manera sencilla de representar los enlaces; un medio para comprender
los diferentes enlaces químicos. Los símbolos de los elementos representativos se
muestran así:
2.3.- Enlace Iónico.
Enlace Iónico
Cuando un metal reacciona con un no metal para adquirir la configuración electrónica
del gas noble inmediato, se transfieren electrones de los átomos del metal a los del no
metal y se forma un compuesto iónico o electrovalente. Los átomos de los no metales se
convierten en iones positivos o cationes por la perdida de electrones y los átomos de los
no metales, al ganar electrones, forman iones negativos o aniones. Los iones formados
se atraen entre sí y forman un cristal.
Enlace iónico es la unión de un metal con un no metal por transferencia de
electrones; es decir, es la unión debida a la perdida de electrones del metal y a la
ganancia de electrones del no metal, formándose iones con carga opuesta.
Enlace iónico es la fuerza de atracción electrostática entre iones de carga opuesta
formados por transferencia de electrones.
Consideremos la reacción entre un átomo de sodio (metal) que está en el grupo I-A con
un átomo de cloro (no metal) que pertenece a la familia VII A.
El sodio reacciona con el cloro para formar cloruro de sodio.
2Na
+
Cl2
2NaCl
De acuerdo con la regla del octeto, estos átomos al combinarse deben adquirir la
configuración del gas noble inmediato. En este caso cuando el sodio se combina,
adquiere por pérdida de un electrón la configuración del neón, que es 1s2 2s2 2p6; deja
así ocho electrones en su último nivel energético y forma una especie química con carga
1+.
Na
1s2 2s2 2p6
3s1
Na+
11 protones 11 1 electrón de
electrones
valencia
1s2 2s2 2p6
11protones
10electrones
Nivel externo
con
8
electrones
Ion Na+
A su vez, el cloro al combinarse con el sodio tiende a ganar un electrón formando un ion
negativo y adquiriendo la configuración del argón, 1s2 2s2 2p6 3s2 3p6, que es el gas
noble inmediato.
Cl
1s2 2s2 2p6
3s23p5
17 protones 7 electrones de
17
valencia
electrones
Cl
1s2 2s2 2p63s23p6
17
protones
electrones
18 Nivel externo
con
8
electrones
Ion
La reacción entre estos dos elementos implica la transferencia de un electrón del átomo
de sodio (metal) el átomo de cloro (no metal) para formar iones sodio Na+ y iones
cloruro Cl-, que tiene carga opuesta y se atraen mutuamente formándose un enlace
iónico.
En la reacción, el número total de electrones perdidos por los átomos de sodio
involucrados, debe ser igual al número total de electrones ganados por los átomos de
cloro y, por consiguiente, el número de iones de sodio obtenidos es igual al de iones
cloruro producidos y la fórmula NaCl da la proporción más sencilla de iones presentes
en el compuesto. Estos iones se atraen mutuamente y forman un cristal.
Los iones se enlazan como conjuntos y se arreglan en el estado sólido siguiendo un
patró_n
tridimensional que forma una red cristalina en donde los iones positivos y
negativos ocupan posiciones específicas de acuerdo con su tamaño y su carga.
En el caso de la red cristalina de cloruro de sodio, ningún ion puede considerarse como
perteneciente exclusivamente al otro. Por lo contrario, cada ion sodio se encuentra
rodeado y equidistante de seis iones cloruro y a su vez cada ion cloruro está rodeado y
equidistante de seis iones sodio. Debido a la disposición de los iones en el cristal, la
repulsión de iones de la misma carga es superada por la atracción de los iones de la
carga contraria que mantienen al cristal junto.
Es por esto que no es posible referirnos a ninguna molécula en particular en el estado
sólido. La totalidad del cristal constituye una macromolécula. La fórmula NaCl para el
cloruro de sodio representa en realidad una fórmula empírica, pues sólo nos indica una
simple relación de iones Na+ a iones Cl -.
En las reacciones iónicas, debido a la pérdida o ganancia de electrones, los elementos
de los grupos A formar iones isoelectrónicos (la misma configuración electrónica) con
un gas noble. Por lo general, estos iones tienen ocho electrones en el nivel externo,
excepto aquellos que adquieren la del helio, que es 1s2.
El berilio (grupo II A) y el flúor (grupo VII A) reaccionan entre sí para formar fluoruro
de berilio (BeF2) de manera análoga al sodio y al cloro, pero con la diferencia
electrónica del 4Be : 1s2 2s2.
El berilio posee dos electrones de valencia.
Configuración electrónica del 9F : 1s2 2s2 2p5.
El flúor tiene siete electrones de valencia.
Debido a que el número de electrones perdidos por los átomos metálicos debe ser igual
al número de los ganados por los no metálicos, por cada átomo de berilio se necesitarán
dos de flúor para formar el compuesto iónico BeF2.
El cloro y el flúor que pertenecen al mismo grupo (VII A) tienen un comportamiento
semejante al unirse a los metales, ambos ganan un electrón formando iones 1-; esto nos
indica que todos los elementos de una fammilia en igualdad de condiciones actuarán en
forma similar.
En general, el enlace iónico se forma entre metales de baja electronegatividad, que
tiende a ceder electrones, y no metales de alta electronegatividad, que tienden a
aceptarlos.
Elemento
Electronegatividad
Diferencia
de Enlace iónico
electronegatividad
Na
0.9
3.0 - 0.9 = 2.1
Na+ Cl
Cl
3.0
Be
1.5
4.0 - 1.5 = 2.5
Be2+ F2-
F
4.0
2.4.- Enlace Covalente.
Enlace Covalente
El enlace covalente es el formado al compartir uno o más pares de electrones.
Generalmente, estos enlaces están formados por átomos de elementos no metálicos de
electronegatividad semejante. Este tipo de enlace fue propuesto inicialmente en 1916,
por G.N. Lewis, quien explicó que se podían formar moléculas del mismo elemento,
como el O2, H2, Cl2, así como de elementos diferentes, como el HCl o el H2O.
Cuando se acercan dos átomos del mismo elemento, existe una interacción mutua entre
sus orbitales y sus núcleos. La nube electrónica forma un enlace con el núcleo y éste
atrae fuertemente a los electrones de los orbitales parcialmente llenas, lo que origina el
enlace químico.
Los átomos que se enlazan de esta manera tienen carga eléctrica neutra, puesto que
todos los electrones de los dos átomos participan en la interacción de los dos núcleos y
ésta tiene particular importancia.
La unión química formada cuando dos átomos comparten electrones se llama enlace
covalente. Se distinguen tres tipos de covalencia: polar, no polar y coordinada.
Ejemplos: la molécula de cloro está formada por dos átomos de cloro; cada cloro tiene
siete electrones en su configuración electrónica externa y un electrón impar en 3p; al
compartir cada átomo un electrón, se completa el orbital y se forma la molécula de
cloro; este enlace se llama covalente simple.
17Cl
= 1s2 2s2 2px2 2py2 2pz2 3s2 3px2 3py2 3pz1
17Cl
= 1s2 2s2 2px2 2py2 2pz2 3s2 3px2 3py2 3pz1
Representación del enlace del cloro mediante el modelo de Lewis. Los dos círculos del
centro son los electrones compartidos.
Los enlaces covalentes pueden ser: simples cuando comparten un sólo par de electrones;
dobles cuando comparten dos pares de electrones; triples cuando comparten tres pares
de electrones; cuádruples cuando comparten cuatro pares de electrones.
ENLACE COVALENTE NO POLAR
Naturaleza del enlace. Se tiene cuando dos átomos de un mismo elemento se unen
formando una molécula verdadera, sin carga eléctrica, simétrica y cuya diferencia de
electronegatividad es cero.
Ejemplos:
1.Molécula de hidrógeno:
El par de electrones compartidos se representa por una línea que une los símbolos de los
átomos.
H —— H (H2)
Se puede esquematizar esta unión para visualizar la forma de la molécula, que en
realidad es una nube debido al movimiento de los electrones.
El par de electrones compartidos están en el centro, a igual distancia de cada núcleo.
2. Molécula de oxígeno:
(O2) (O = O)
Otras moléculas: F2, Cl2, Br2, I2
Propiedades de las sustancias con este tipo de enlace




Moléculas verdaderas y diatómicas (con dos átomos).
Actividad química, media.
No son conductores del calor o la electricidad.
Estado físico, gaseoso aunque pueden existir como sólidos o líquidos.
Enlace covalente polar
Naturaleza del enlace. Cuando dos átomos no metálicos de diferentes
electronegatividades se unen, comparten electrones pero la nube electrónica se deforma
y se ve desplazada hacia el étomo de mayor electronegatividad, originando polos en la
molécula, uno con carga parcialmente positiva y el otro con carga parcialmente
negativa.
En general, la diferencia de electronegatividades es menor a 1.7. Existen casos como el
HF que se considera un enlace iónico propiamente, pero es covalente por ser dos átomos
no metálicos lo que se unen.
Ejemplos:
Formación de la molécula de fluoruro de hidrógeno.
d+ H— F dOtras sustancias con este tipo de enlace:
H2O, HBr, PCl3, SO2, NH3, H2SO4, HNO3, CH3COOH
Propiedades de las substancias con este tipo de enlace





Moléculas que existen en los tres estados físicos de agregación de la masa.
Gran actividad química
Solubles en solventes polares
Solución acuosa son conductores de la electricidad
Sus puntos de fusión y ebullición son bajos, pero más altos que los de las
substancias no polares
Enlace covalente coordinado
Naturaleza del enlace. Un átomo no metálico comparte un par de electrones con otro
átomo pero el segundo los acomoda en un orbital vacío. Se dice entonces que el primer
átomo da un par de electrones o que ambos átomos se coordinan para completar su
octeto.
Ejemplo:
H2SO4 (ácido sulfúrico)
La coordinación de los electrones entre átomos o bien de qué átomo a que átomos van
los electrones compartidos se indica con una flecha.
Asi, en el ejemplo anterior se ve que los electrones van del azufre al oxígeno.
2.4.3.- Geometrías moleculares: RPECV
Tres modelos describen la geometría y los enlaces moleculares:
» Modelo de repulsiones electrón-electrón (RPENV),
» Teoría del enlace de valencia,
» Teoría de los orbitales moleculares.
Formas Moleculares
Las estructuras de Lewis no indican la forma de las moléculas: sea, por ej., la
molécula de CCl4.
Las moléculas del tipo ABn son muy comunes: CO2, H2O, SO3 NH3, etc. La
forma que pueden adoptar depende del valor de n, como se muestra a
continuación:
El modelo RPENV
» ¿Por qué diferentes moléculas AB2 adoptan formas distintas?
» ¿Se pueden predecir las formas de las moléculas?
El mejor acomodo de pares, es el que minimiza sus repulsiones
Mecanismo para predecir la geometría molecular:
Al describir la forma de una molécula, siempre se indica la geometría
molecular, no la geometría de los pares de electrones.
Mecanismo para predecir la geometría molecular:
La geometría molecular se describe en términos de la disposición
angular de los pares enlazantes.
Para moléculas con enlaces múltiples, el modelo
RPENV toma éstos
como un par enlazante para predecir la geometría.
2.4.4.- Enlaces Covalentes y traslape de orbitales.
El modelo RPENV predice la forma de las moléculas pero no explica la
existencia de enlaces.
La teoría del enlace covalente aborda el problema mediante el uso de la
mecánica cuántica.
El uso de orbitales atómicos conduce a la teoría del enlace de valencia
(TEV)
En la teoría de Lewis el enlace es el resultado de la compartición de
electrones, en la TEV los orbitales comparten una región del espacio, es decir,
se traslapan.
El traslape permite que dos electrones con espín opuesto formen un
enlace covalente.
En la molécula de H2 el traslape de orbitales concentra la densidad electrónica
entre los núcleos:
El traslape de orbitales concentra la densidad electrónica en regiones
específicas
2.4.5.- Orbitales Híbridos.
Es la mezcla de orbitales atómicos, no sólo el traslape, para generar orbitales
“nuevos”, ¿por qué?:
Sea la molécula de BeF2: Lewis forma lineal con 2 enlaces F-Be idénticos;
F — Be — F
Diagrama orbital:
Orbitales híbridos sp
El átomo de Be “promueve” un e- del 2s al 2p:
Los electrones 2s y 2p no tienen la misma energía, ¿cómo forman
entonces dos enlace iguales con F?
Se han creado 2 orbitales híbridos nuevos (sp) mezclando dos o más
orbitales atómicos.
Hibridación sp
Los orbitales híbridos sp son equivalentes en tamañoy energía, apuntando en
direcciones opuestas (180º)
Los electrones de los orbitales híbridos sp pueden formar enlaces de
electrones compartidos con los dos átomos de F, con una geometría lineal:
Orbitales híbridos sp2
La mezcla de un orbital 2s y dos orbitales 2p produce tres orbitales sp2.
Orbitales híbridos sp3d
Los átomos del tercer periodo en adelante pueden utilizar orbitales d para
formar orbitales híbridos spd.
2.4.6.- Momentos bipolares.
MOMENTO BIPOLAR. El producto de la distancia que separa cargas opuestas de
igual magnitud y la magnitud de la carga; una medida de polaridad de un enlace o
una molécula. Un momento bipolar medido que refiere al momento bipolar de una
molecular entera.
2.4.7.- Enlaces Múltiples.
Enlaces Múltiples: Para cada par de electrones compartidos entre dos átomos, se
forma un enlace covalente único. Algunos átomos pueden compartir múltiples pares
de electrones, formando enlaces covalentes múltiples. Por ejemplo, el oxígeno (que
tiene seis electrones de valencia) necesita dos electrones para completar su envoltura
de valencia. Cuando dos átomos de oxígeno forman el compuesto O2, ellos comparten
dos pares de electrones, formando dos enlaces covalentes.
2.5.- Enlace Metálico y Elementos semiconductores.
Enlace metálico
La plata, un metal típico, consiste en una formación regular de
átomos de plata que han perdido cada uno un electrón para formar
un ion plata. Los electrones negativos se distribuyen por todo el
metal formando enlaces no direccionales o deslocalizados con los
iones plata positivos. Esta estructura, conocida como enlace metálico,
explica las propiedades características de los metales: son buenos
conductores de la electricidad al estar los electrones libres para
moverse de un sitio a otro, y resultan maleables porque sus iones
positivos se mantienen unidos por fuerzas no direccionales.
Semiconductores
Los elementos del Grupo IVA de la tabla periódica (C, Si, Ge, Sn) tienen
dos electrones en su capa p externa, y valencia de 4. Se espera que estos
elementos tengan una alta conductividad debido a que la banda p no está llena.
Sin embargo, tal comportamiento no ocurre. Estos elementos están enlazados
de manera covalente; en consecuencia, los electrones de las bandas exteriores
s y p están rígidamente unidos a los átomos. Las restricciones provocadas por
el enlace covalente producen un cambio complejo en la estructura de las
bandas, produciéndose una hibridación. Los niveles 2s y 2p de los átomos de
carbono en el diamante pueden contener hasta ocho electrones, pero sólo hay
cuatro electrones de valencia disponibles. Cuando se juntan N átomos de
carbono para formar un diamante sólido, los niveles 2s y 2p interactúan y
producen dos bandas que no se traslapan. Cada una de las bandas híbridas
puede contener 4N electrones. Puesto que hay sólo 4N electrones disponibles,
la banda inferior o de valencia se llena completamente mientras que la superior
o de conducción se encuentra vacía. Una brecha o banda de energía Eg
separa los electrones de la banda de conducción. Son pocos los electrones que
poseen la energía suficiente para rebasar la zona prohibida hacia la banda de
conducción. En consecuencia, el diamante es un excelente aislante eléctrico.
Un comportamiento similar se observa en casi todos los materiales enlazados
de modo covalente y de modo iónico. Aunque el germanio, el silicio y el estaño
tienen la misma estructura cristalina y de bandas que el diamente, la brecha de
energía es menor. De hecho, la banda de energía en el estaño es tan pequeña
que normalmente se comporta como un metal. La banda o brecha es algo
mayor en el silicio y en el germanio -estos elementos se comportan como
semiconductores.
Semiconductores intrínsecos
Debido a que la banda de energía Eg es pequeña en el silicio y en el
germanio, pocos electrones poseen suficiente energía térmica para excitarse
en la banda de conducción. Los electrones excitado dejan tras de sí niveles de
energía no ocupados, o huecos, en la banda de valencia. Cuando se aplica un
voltaje al material los leectrones en la banda de conducción se aceleran hacia
la terminal positiva, mientras que los huecos se mueven hacia la terminal
negativa. Por esto, la corriente es conducida por el movimiento tanto de los
electrones como de los huecos, los cuales actúan como electrones cargados
positivamente. El material se comporta como un semiconductor intrínseco. La
conductividad está determinada por el número de pares electrón-hueco.
donde ne es el número de electrones en la banda de conducción, nh es el
número de huecos en la banda de valencia, y mue y muh son las movilidades
de los electrones y los huecos. En los semiconductores intrínsecos,
n = ne = nh
Por lo tanto, la conductividad es
Conforme se incrementa la temperatura, hay una mayor probabilidad de que un
nivel de energía en la banda de conducción esté ocupado (y una probabilidad
igual de que sea creado un hueco en la banda de valencia). El número de
electrones en la banda de conducción, o el número de huecos en la banda de
valencia, está relacionado con la temperatura y la capa de energía por:
donde no puede ser considerada constante. Debido a que las temperaturas
más elevadas permiten que más electrones atraviesen la zona prohibida, la
conductividad se incrementa.
El comportamiento del semiconductor es opuesto al de los metales. Cuando la
temperatura se incrementa, la conductividad de un semiconductor se
incrementadebido a que hay un número mayor de los portadores de carga,
mientras que la conductividad de un metal disminuye debido a la menor
movilidad de los portadores de carga.
Semiconductores extrínsecos
No se puede controlar con precisión el comportamiento de un semiconductor
intrínseco, puesto que las pequeñas variaciones en la temperatura cambian la
conductividad. Sin embargo, añadiendo intencionalmente un pequeño número
de átomos como impurezas al material, se puede producir un semiconductor
extrínsecos. La conductividad del semiconductor extrínseco depende
fundamentalmente del número de átomos de impurezas, o impurificantes
(dopantes), y en un cierto intervalo de temperatura puede ser incluso
independiente de la temperatura. La conductividad es por esto controlable y
estable.
Semiconductores tipo n
Supóngase que se añade un átomo de impureza como el antimonio, el cual
tiene valencia 5, al silicio o al germanio. Cuatro de los electrones del átomo de
antimonio participan en el proceso de enlace covalente, mientras que el
electrón adicional ocupa un nivel de energía en un estado donador justo por
debajo de la banda de conducción. Puesto que el electrón adicional no está
estrechamente enlazado con los átomos. se requiere tan sólo una pequeña
energía Ed para que el electrón entre a la banda de conducción. Se ha
producido así un semiconductor tipo n. No se crean huecos correspondientes
cuando los electrones de donador ocupan la banda de conducción. A bajas
temperaturas, se producen pocos electrones y huecos intrínsecos y el número
de electrones es de aproximadamente.
donde nod es constante. Cuando se incrementa la temperatura, un número
mayor de electrones de donador saltan la brecha Ed hasta que, finalmente, la
totalidad de los electrones de donador entra a la banda de conducción. En este
punto se ha alcanzado el agotamiento del donador. La conductividad es
prácticamente constante, puesto que no hay más electrones de donador
disponibles y la temperatura es aún demasiado baja para generar muchos
electrones y huecos intrínsecos. La conductividad es
donde nd es el número máximo de electrones donadores, determinado por el
número de átomos de impurezas que se añaden. Se prefiere operar en el
intervalo de temperatura de agotamiento. Generalmente, los semiconductores
con una gran Eg tiene la meseta de agotamiento más ancha. A altas
temperaturas, la semiconducción intrínseca se vuelve importante y la
conductividad aumenta de nuevo de acuerdo con la relación
Semiconductores tipo p
Cuando se añade una impureza como el galio, que tiene valencia 3, a un
semiconductor, no hay electrones suficientes para completar el proceso de
unión covalente. Un hueco electrónico se crea en la banda de valencia, el cual
puede ser llenado por electrones provenientes de otros lugares en la banda.
Estos lugares huecos tienen una energía algo mayor que la normal y crean un
nivel de aceptador de posibles energías electrónicas justo por encima de la
banda de valencia. Un electrón debe ganar una energía de sólo Ea para poder
crear un hueco en la banda de valencia. El hueco se mueve entonces y
transfiere la carga. Ahora se tiene un semiconductor tipo p. A bajas
temperaturas, predominan los niveles del aceptador.
Finalmente, la temperatura es suficientemente alta para causar una saturación
de aceptadores y
donde na es el número máximo de niveles de aceptadores, o huecos,
introducido por el impurificante.
A temperaturas mayores la semiconducción intrísica se hace importante y
Compuestos semiconductores
El silicio y el germanio son los únicos elementos que tienen aplicación práctica
como semiconductores. Sin embargo, eun gran número de compuestos
muestran el mismo efecto. Produciéndose intencionalmente compuestos que
se desvíen ligeramente de las propiedades estequiométricas, se pueden hacer
semiconductores tipo n o tipo p. En algunos de estos compuestos, como el
Gaas tipo n, una gran bandad de energía conduce a una meseta ancha de
agotamiento, mientras que la alta movilidad electrónica proporciona una alta
conductividad.
2.6.- Fuerzas Intermoleculares y propiedades físicas.
Las
fuerzas
intermoleculares.
La fuerza molecular, consiste en la atracción o la repulsión, de naturaleza
eléctrica, de moléculas entre sí. Son las que determinan las distancias de las
moléculas entre ellas, y son las causantes de choques entre las moléculas y de
los movimientos dentro de un material.
Fuerzas Intermoleculares
En una molécula, los átomos se mantienen unidos por medio de enlace covalentes; la
estructura y la forma molecular están determinados por las propiedades de los átomos
constituyentes y los enlaces químicos entre ellos.
El hecho de que substancias formadas por moléculas independientes se encuentren en
estado líquido y sólido, señala que deben de existir fuerzas de atracción entre las
moléculas. Ahora bien, la mayoría de las reacciones químicas involucran interacciones
moleculares, por lo que es importante considerar este tipo de fuerzas intermoleculares,
cuya magnitud se refleja en propiedades como el calor de fusión, de vaporización,
solubilidad, etc. Entre las fuerzas intermoleculares se tiene: las dipolo-dipolo, enlace de
hidrógeno, etcétera.
Tipos de Fuerzas
Van der Waals.
Las fuerzas de Van der Waals son aquellas interacciones intermoleculares que tienen
como característica ser las más débiles. Otra particularidad es que se llevan a cabo entre
moléculas no polares, pero debido al movimiento continuo de los electrones se
producen ligeras cargas negativas y positivas a lo largo de las moléculas y las
atracciones entre los polos opuestos, originándose precisamente las fuerzas de Van der
Waals. Estas fuerzas son todas de atracción en la naturaleza y juegan un papel
importante en la determinación de las propiedades físicas de las sustancias, tales como
puntos de fusión, puntos de ebullición y solubilidades.
La distancia entre moléculas (o especies monoatómicas) en un sólido o líquido está
determinada por el balance entre fuerzas de Van der Waals de atracción y las fuerzas de
repulsión entre los electrones y entre los núcleos. El radio de Van der Waals es la mitad
de la distancia entre dos átomos no enlazados equivalentes en su distribución más
estable, esto es, cuando las fuerzas netas de atracción están al máximo.
La diferencia principal entre el radio atómico y el radio iónico, por un lado, y el radio de
Van der Waals, por otro lado, es que este último se aplica a átomos que no están
enlazados químicamente entre sí. Por ejemplo dos átomos de helio no se combinan para
formar la molécula de He2, pero los átomos de He sí se atraen mediante las fuerzas de
dispersión. Es posible imaginar, en el He líquido, que los átomos se atraen entre sí hasta
que las fuerzas netas de atracción están al máximo. Si dos átomos vecinos cualesquiera
son obligados acercarse más, las fuerzas de repulsión entre los electrones y entre los
núcleos provocarían que el sistema perdiera estabilidad. En las condiciones de máxima
atracción, la mitad de la distancia entre dos átomos de He adyacentes en helio líquido es
el radio de Van der Waals del átomo de He.
La tabla 1 muestra los radios de Van der Waals de algunos átomos escogidos
acomodados en orden creciente de número atómico.
Atomo
Radio de Van
Waals (pm)
der
H C N O F P 120 165 150 140 135
S Cl Br I
190 185 180 195 215
Dipolo-Dipolo
Las fuerzas dipolo-dipolo existen entre moléculas polares neutras. Las moléculas
polares se atraen unas a otras cuando el extremo positivo de una molécula está cerca del
extremo negativo de otra, como se ilustra en la figura 3.5.1.2 a) y b). Las fuerzas dipolodipolo son efectivas sólo cuando las moléculas polares están muy próximas.
Fig. 3.5.1 Atracción dipolo-dipolo en el HCl.
En los líquidos, las moléculas dipolares están libres para moverse unas respecto a otras.
Algunas veces tendrán una orientación en que se atraen y otras una orientación en que
se repelen. Dos moléculas que se atraen pasan más tiempo cerca una de la otra que dos
partículas que se repelen entre sí. Así, el efecto general es una atracción neta. Cuando
examinemos varios líquidos encontraremos evidencia de que para moléculas de masa y
tamaño semejante, las energías de las atracciones intermoleculares aumentan cuando la
polaridad aumenta. Podemos apreciar esta tendencia en los líquidos que se enumeran en
la tabla 1. Los puntos de ebullición aumentan cuando el momento dipolar aumenta.
Tabla 1 Masas moleculares, momentos dipolares, y puntos de ebullición de sustancias
orgánicas sencillas.
Sustancia
Masa molecular Momento
(uma)
dipolar µ (D)
Punto
de
ebullición (K)
Propano, CH3CH2CH3
44
0.1
231
Eter dimetílico CH3OCH3
46
1.3
249
Cloruro de metilo CH3Cl
50
2.0
249
Acetaldehido, CH3CHO
44
2.7
293
Acetonitrilo, CH3CN
41
3.9
355
Puente de Hidrógeno
Este tipo de fuerza es un tipo especial de atracción intermolecular que existe entre el
átomo de hidrógeno de un enlace polar (sobre todo un H-O, H-N o H-F) y un par de
electrones no compartidos en un átomo electronegativo (O, N, F) de una molécula
vecina.
Puente de hidrógeno es la unión de dos átomos electronegativos por medio de un
hidrógeno que sirve de puente entre ambos, unidos a uno covalentemente y a otro por
fuerzas electrostáticas.
El enlace de hidrógeno se puede presentar tanto entre moléculas idénticas de un
compuesto puro como entre moléculas diferentes, pero se requiere que:
a) El átomo que proporciona el par de electrones para el enlace sea relativamente
pequeño y muy electronegativo.
b) La molécula que suministra el hidrógeno para formar el enlace sea muy polar.
La atracción molecular por puente de hidrógeno se puede presentar entre las mismas o
diferentes moléculas. Se señala con una línea de puntos (....), La interacción se escribe
como:
A-H¨¨B o A-H¨¨A
Ejemplos:
a) Molécula de agua
b) Molécula del ácido fluorhídrico
c) Puente de hidrógeno entre la molécula de agua y éter111
Los átomos electronegativos más grandes, por tener nubes electrónicas más difusas,
muestran poca o ninguna tendencia a formar enlaces de hidrógeno.
La energía para romper un enlace de hidrógeno es mucho más débil que la que se
necesita para romper un enlace covalente; sin embargo, es un tipo de fuerza
intermolecular bastante importante porque ejerce gran influencia en las propiedades de
un compuesto.
La gran solubilidad de compuestos que contienen oxígeno, nitrógeno y flúor se debe
también a la formación de enlaces de hidrógeno. El amoníaco es muy soluble en agua
mediante la formación de este tipo de enlaces.
Las moléculas que presentan atracción por puente de hidrógeno tienen puntos de
ebullición mayores, comparados con los compuestos análogos de los elementos del
mismo grupo.
En la figura X se observa que en los hidrocarburos polares de los grupos V, VI Y VII el
punto de ebullición aumenta al aumentar la masa molecular, excepto para los primeros
miembros de estos grupos. En el grupo IV, que forma hidruros no polares, existe una
relación casi lineal entre el aumento del punto de ebullición y la masa molecular, debido
a la ausencia de interacciones dipolo-dipolo.
Figura 3.5.1.3 Comparación del punto de ebullición de: H2O, HF y NH3, con
compuestos similares de elementos de su mismo grupo.
2.6.1.- Van der Waals: dipolo-dipolo, London, Puente de PH.
FUERZAS DIPOLO-DIPOLO
Las fuerzas dipolo-dipolo existe entre moléculas polares neutras
• Son efectivas cuando las moléculas están muy juntas
• Son más débiles que las ion-dipolo.
FUERZAS DE DISPERSIÓN DE LONDON
Fuerza de atracción existente entre moléculas no polares, mediante
dipolos instantáneos generado por el movimiento de los electrones.
(polarizabilidad).
Las fuerzas de dispersión de London aumenta, cuando aumentan el tamaño del
átomo.
Las fuerzas de dispersión están presentes en todas las moléculas.
PUENTES DE HIDRÓGENO
Interacción que existe entre un átomo de hidrógeno de un enlace polar (HN, HO, HF,
etc.) y un par de electrones no compartidos en un ion o átomo electronegativo cercano
de otra molécula, usualmente (F, O, N).
Sus interacciones son más fuertes que las dipolo-dipolo y London.
2.7.1.- Estado sólido (cristalino).
LA ESTRUCTURA CRISTALINA
Un sólido cristalino, o cristal, es una ordenación periódica de estructuras idénticas.
La estructura idéntica que se repite, recibe el nombre de base cristalina. La estructura
sobre la que se repite, el de red cristalina, (Fig.1.1).
Figura 1.1.- Cristal, celdilla primitiva y celdilla de
Wigner- Seitz en dos dimensiones
Tres vectores, , a b y c r r r definen una red cristalina a través de tres enteros n1, n2 y
n3, de modo que si 0 r r es el vector de posición de un punto de la red, el expresado por:
0 r = r +Tr r r (1.1) también lo es. El vector 1 2 3 T = na + n b + n c r r r r (1.2) define
el grupo de traslaciones del cristal. En toda red cristalina se pueden encontrar (y no de
forma única) tres vectores de forma que dos puntos reticulares cualesquiera están
siempre relacionados por una expresión del tipo (1.1) con n1, n2 y n3 enteros. Los
vectores y a, b c r r rque cumplen también esto, definen una celdilla que también por
traslación genera el cristal. Se la llama celdilla primitiva porque es la de volumen
mínimo que por traslación reproduce el cristal. Si hubiera otra de menor volumen y
tomando n1, n2 y n3 enteros, no encontraríamos necesariamente
un punto reticular (Fig. 1.1). Es fácil comprender que a cada celdilla primitiva le
corresponde un solo punto reticular (con su correspondiente base cristalina). La celdilla
primitiva no es única. Una forma de concretar la celdilla primitiva es bisecar por planos
los segmentos que unen un punto reticular a sus próximos vecinos. En este caso recibe
el nombre de celdilla elemental de Wigner-Seitz (Fig. 1.1) y cumple con los
postulados anteriores. En particular, es evidente que sólo contiene un punto reticular.
Las redes cristalinas se llaman también redes de Bravais y hay 14 diferentes agrupadas
en 7 sistemas
cris talinos (Fig. 1.2).
2.7.2.- Concepto y caracterización de sistemas cristalinos.
Los sistemas cristalinos
Los
cristales
se
describen
por
los
sistemas
cristalinos.
Se pueden observar el análisis de un cristal considerando un cubo (fig. 1.4.1).
Existen 7 sistemas cristalinos y cada uno de ellos tiene sus propios elementos de
simetría.
Se describen los sistemas cristalinos por:
Sus
ejes
cristalográficos.
- Los ángulos que respectivamente dos de los ejes cristalográficos rodean.
- Las longitudes de los ejes cristalográficos.
1. Se fijarán el aspecto obvio que todas las caras están perpendiculares entre sí.
2. Hay tres planos de simetría, que están perpendiculares entre sí y los cuales se llaman
'planos axiales de simetría'. Cada cara a un lado de este plano de simetría se refleja a su
otro lado. También se pueden coger dos caras opuestas del cubo entre pulgar y índice
asi incluyendo un eje de simetría y girar el cubo para encontrar un eje cuaternario de
simetría. Es decir que por una rotatión completa de 360° una cara se repite cuatro veces.
Un otro eje de simetría entre las esquinas opuestas del cubo es un eje ternario de
simetría. De los mismos hay cuatro en el cubo. Un eje de simetría perpendicular a un
par de aristas opuestas es un eje binario de simetría, de los cuales existen seis en el
cubo.
3. El aspecto esencial de la simetría es el siguiente: se pueden realizar una operación
geométrica en tal manera que una cara se repite en una otra posición. Es decir que al
realizar una operación geométrica como una rotación p. ej. una cara nueva ocupará la
misma posición que fue ocupado por una otra cara antes de la rotación y con la
consecuencia que no pueden distinguirse entre la apariencia después la rotación y la
apariencia original.
Simetría
de
un
cubo
según
PHILLIPS
&
PHILLIPS
(1986):
Zona: Un grupo de caras que se interceptan formando aristas paralelas, se dice que
constituyen una zona. Eje de zona: La dirección de las líneas de intersección entre las
caras
de
una
zona,
se
llama
eje
de
zona.
1. El cubo exhibe tres conjuntos de aristas paralelas, por tanto se compone de tres zonas.
Las tres ejes de zona son ortogonales. Las seis caras del cubo son idénticas, cada una de
ellas es paralela a dos ejes de zona y perpendicular al tercer eje de zona. En
consecuencia el cubo es una forma de seis lados, que encierre completamente a un
espacio.. Por ello, a la forma cúbica de designe como una forma simple.
2. Cuando una misma cara del cubo de observa en cuatro posiciones diferentes durante
la rotación, el eje paralelo de las aristas es un eje de simetría cuarternario, el cual se
denomine eje cuarternario. En el cubo hay tres ejes cuarternarios.
3. Puesto que las caras del cubo tienen la misma orientación en tres posiciones durante
una rotación completa, el eje que pasa por las esquinas de un cubo perfectamente
simétrico puede describirse como un eje de simetría ternario o un eje ternario. Ya que
los ejes ternarios unen esquinas opuestas del cubo deberán existir cuatro ejes ternarios.
4.Cuando se gira sobre un eje perpendicular a un par de aristas opuestas y la imagen del
cubo se repite dos veces, el eje es de simetría binaria y se llama eje binario. En vista de
que hay seis pares de aristas opuestas en el cubo éste debe tener seis ejes binarios
Sistema cúbico
Existen tres ejes cristalográficos a 90° entre sí:
alfa = beta = gama = 90°
Las longitudes de los ejes son iguales:
a=b=c
Formas típicas del sistema cristalino y sus elementos de simetría :
El cubo (p.ej. halita, fluorita), el rombododecaedro (p.ej. granate) y el octaedro son
formas de 3 ejes cuaternario de simetría, 4 ejes ternarios de simetría y 6 ejes binarios de
simetría.
El Tetraedro es una forma de 4 ejes ternarios y de 3 ejes binarios.
Minerales que pertenecen al sistema cúbico son:
Halita NaCl, Pirita FeS2,Galena PbS, las cuales forman entre otros cubos.
Diamante de forma octaédrica, Magnetita Fe3O4 forma entre otros octaedros.
Granate, p. ej. Almandina Fe3Al2[SiO2]4 de forma rombododecaédrica, de forma
icositetraédrica o de combinaciones de las formas icositetraédrica y rombododecaédrica.
- El rombododecaedro es una forma simple compuesta de 12 caras de contorno rómbico.
El icositetraedro es una forma compuesta de 24 caras de contorno trapezoidal.
Esfalerita ZnS de forma tetraédrica.
Sistema tetragonal
Existen 3 ejes cristalograficos a 90° entre sí:
alfa = beta = gama = 90°
Los parámetros de los ejes horizontales son iguales, pero no son iguales al parámetro
del eje vertical:
a = b ≠ [es desigual de] c
Formas típicas y sus elementos de simetría son :
Circón (ZrSiO2) pertenece al sistema tetragonal y forma p. ej. prismas limitados por
pirámides al extremo superior y inferior.
Casiterita SnO2
Sistema hexagonal
Existen 4 ejes cristalográficos, tres a 120° en el plano horizontal y uno vertical y
perpendicular
a
ellos:
Y1 = Y2 = Y3 = 90° - ángulos entre los ejes horizontales y el eje vertical.
X1 = X2 = X3 = 120° - ángulos entre los ejes horizontales.
a1 = a2 = a3 es desigual de c con a1, a2, a3 = ejes horizontales y c = eje vertical.
Apatito Ca5[(F, OH, Cl)/(PO4)3] y grafita C pertenecen al sistema hexagonal.
Formas típicas son el prisma hexagonal y el trapezoedro hexagonal de un eje sexternario
y 6 ejes binarios.
Sistema trigonal
Existen tres ejes cristalográficos con parámetros iguales, los ángulos X1, X2 y X3 entre
ellos
difieren
a
90°:
X1
=
X2
=
X3
=
90°
a1
=
a2
=
a3
Calcita CaCO3 y Dolomita CaMg(CO3)2 pertenecen al sistema trigonal y forman a
menudo
romboedros.
Otra forma es una combinación de piramide trigonal y pinacoide con 3 ejes binarios de
simetría.
Sistema ortorómbico
Existen tres ejes cristalográficos a 90° entre sí:
alfa = beta = gama = 90°
Los parámetros son desiguales:
a ≠ b ≠ c [a es desigual de b es desigual c]
Ejemplo: Olivino (Mg,Fe)2(SiO4)
Una forma típica es una combinación de paralelogramo y pinacoide con 3 ejes binarios
de simetría.
Sistema monoclínico
Hay tres ejes cristalográficos, de los cuales dos ( uno de los dos siempre es el eje
vertical = eje c) están a 90° entre sí:
alfa = gama = 90° y beta es mayor de 90°
Los parámetros son desiguales.
a ≠ b ≠ c [a es desigual de b es desigual de c]
Ejemplo: Mica
Sistema triclínico
Hay tres ejes cristalográficos, ninguno de ellos a 90° entre sí:
alfa es desigual de beta es desigual de gama es desigual de 90°
Los parámetros son desiguales.
a ≠ b ≠ c [a es desigual de b es desigual de c]
Ejemplo: Albita: NaAlSi308 y Distena: Al2SiO5
2.7.3.- Anisotropía.
Una de las propiedades más destacables de los superconductores basados en óxidos de
cobre es que tanto sus propiedades en el estado normal como las que corresponden al
estado superconductor muestran una gran anisotropía. Esa anisotropía refleja aquella
que se evidencia en la estructura atómica
2.7.9.- Proceso de cristalización y vitrificación vs propiedades fisicoquímica,
modificadores de red.
Cristalización:
La solubilidad de los compuestos en un solvente dado, es la propiedad en que
se basa este método para separar y purificar dos sólidos mezclados entres sí.
La solubilidad se define como la concentración máxima, a una temperatura
dada, que un soluto puede tener en un solvente dado. Se reporta como gramos
de soluto/100 gramos de solvente.
La cristalización es la formación de cristales a partir de una solución
sobresaturada. Durante el proceso de formación de un cristal las moléculas del
compuesto tienden a fijarse sobre un cristal ya existente, que contiene el mismo
tipo de moléculas, ya que encajan mejor en el enrejado cristalino formado por
moléculas de la misma estructura que en aquellos formados por otro tipo de
moléculas. Esta tendencia de las moléculas, a depositarse en las superficies
compuestas por moléculas semejantes producirá un gran aumento en la pureza
del material cristalino obtenido. Para efectuar la separación de dos sólidos por
el proceso de cristalización, deben encontrarse las condiciones en las que uno de
los sólidos que se desea separar sea soluble y el otro no en un solvente
determinado.
Para esto se prueban diferentes solventes y diferentes temperaturas. La mayor
parte de las sustancias presentan cierta solubilidad a una determinada
temperatura. Por lo tanto es común separar dos sustancias en la misma solución
por el proceso llamado cristalización fraccionada.
¿En qué consiste la vitrificación?
La vitrificación es un proceso que atrapa, en forma permanente, los químicos
nocivos en un bloque sólido de material similar al vidrio, y así impide que los
mismos escapen al medio ambiente. La vitrificación puede llevarse a cabo bajo
tierra o en la superficie.
¿Cómo funciona?
El proceso de vitrificación utiliza energía eléctrica para producir el calor
necesario para fundir el suelo. Se implantan varillas, denominadas electrodos,
en el área contaminada. Luego, se envía una fuerte corriente eléctrica entre los
electrodos, lo cual funde el suelo que se encuentra entre ellos. La fundición
comienza cerca de la superficie del suelo y continúa hacia abajo. A medida que
el suelo se funde, los electrodos se hunden más profundamente en la tierra, con
lo cual el suelo más profundo también se funde. Cuando se corta la energía
eléctrica, el suelo fundido se enfría y vitrifica, o se sea convierte en un bloque
sólido de material parecido al vidrio. Los electrodos pasan a formar parte del
bloque. Una vez vitrificado, el volumen original del suelo se reduce. Esto hace
que la superficie del suelo en el área quede levemente deprimida. Esta área se
rellena con suelo limpio a fin de nivelar el suelo. La temperatura utilizada para
fundir el suelo puede, al mismo tiempo, destruir algunos químicos nocivos y
causar la evaporación de otros. Los químicos evaporados ascienden hasta la
superficie a través del suelo fundido. Allí, una cubierta colocada sobre el área
tratada captura los químicos, que son enviados a un sistema de tratamiento
donde son eliminados.
UNIDAD 3.- REACCIONES INORGÁNICAS, SU ESTEQUIOMETRÍA, SU
IMPORTANCIA ECONÓMICA, INDUSTRIAL Y AMBIENTAL.
3.1.- Clasificación de las Reacciones.
Reacción Química.
Es la acción por la cual dos o más cuerpos dan lugar a nuevas sustancias o compuestos.
Normalmente toda reacción química lleva consigo un intercambio de energía.
La reacción química se representa, abreviadamente por una ecuación química que es
igual que se exprese de la siguiente forma:
A +
B
C +
REACTIVOS
D
PRODUCTOS
R. de combinación.
Este tipo de reacción ocurre cuando se forma una sustancia o compuesto a partir de la
combinación química o unión de dos o más elementos o compuestos.
Su fórmula general es:
A + B
AB
Ejemplos:
2H2 + O2
2H2O
C +
CO2
O2
NH3 + H2O
NH4OH
R. de descomposición.
Es el proceso inverso al anterior. Se habla de descomposición cuando un compuesto se
fracciona en dos o más cuerpos de composición más simple.
Su fórmula general es:
AB
A
+
B
Ejemplos:
2H2O
2H2
+ O2
2HgO
2Hg + O2
También aquellas en que un compuesto se descompone en otros compuestos.
Ejemplos:
CaCO3
CaO
NH4Cl
NH3
+
CO2
+ HCl
R. de sustitución.
En esta reacción por desplazamiento se verifica que uno de los elementos de estos
compuestos son desplazados por otros (con frecuencia los elementos son hidrógeno o un
metal).
Su fórmula general es:
AB +
X
AX + B
Ejemplos:
2AgCl
+
Fe
FeCl
+
2Ag
2HCl
+
Zn
ZnCl2
+
H2
H2SO4
+
Mg
MgSO4 +
H2
R. de neutralización.
Las soluciones de ácidos y bases tienen propiedades muy diferentes. Los ácidos tienen
un sabor ácido, en tanto que las bases tienen un sabor amargo.
Cuando la solución de un ácido se mezcla con la solución de una base, se efectúa una
reacción de neutralización. Los productos de la reacción no tienen las propiedades
características ni de las soluciones ácidas, ni de las básicas difieren mucho en sus
propiedades químicas.
En general, una reacción de neutralización entre un ácido y un hidróxido metálico
produce agua y una sal.
Ejemplo:
HCl(ac) + NaOH(ac)
H2O(l) + NaCl(ac)
(ácido)
(agua)
(base)
(Sal)
R. de óxido-reducción.
Son reacciones que implican una transferencia de electrones de una sustancia a otra. Se
puede presentar de diferentes maneras: en forma iónica, por dos semirreacciones o en
forma molecular. Ejemplo:
3Cu +
8HNO3
3Cu0
3Cu(NO3)2 + 2NO + 4H2O
Reacción
de
óxido
reducción molecular.
-
6e-
3Cu+2
2NO3- + 6e-
+
8H+
2NO +
4H2O
3Cu0 + 2NO3-
+
8H+
3Cu+2 +
2NO + 4H2O Reacción de oxidaciónreducción iónica
Semirreacción
oxidación
de
Semirreacción
reducción
de
3.2.- Balanceo de Ecuaciones Químicas.
Balanceo de ecuaciones químicas.
Para que un cambio químico quede representado correctamente por una ecuación, ésta
debe cumplir con lo siguiente:
1. Determinar cuáles son las substancias iniciales (reactantes) y cuáles las
resultantes (productos).
2. Escribir los reactantes en un miembro de la ecuación, por lo general el izquierdo,
y unirlos mediante el signo de adición.
3. Escribir los productos en el otro miembro de la ecuación. Ambos miembros se
unen con una flecha que indica la dirección del cambio.
4. Los símbolos y fórmulas deben ser correctos.
5. Balancear la ecuación.
Balancear significa hacer iguales los dos miembros; es decir, los dos miembros de la
ecuación deben tener el mismo tipo y número de átomos.
Al balancear una ecuación química sólo puede haber cambios en los números de los
coeficientes nunca en los subíndices, ya que si estos se modifican cambia la substancia
participante en la reacción y, por consiguiente, la ecuación resultante no representará el
cambio químico que verdaderamente se efectúa.
3.2.1.- Por el método Redox.
Por el método redox
Una reacción de oxidación- reducción se define como aquella en la cual determinados
átomos o iones monoatómicos de las sustancias que intervienen en la reacción son
oxidados al mismo tiempo que otros son reducidos.
Oxidación: se dice que un elemento se oxida cuando pierde electrones, aumentando sus
números de oxidación positivos y disminuyendo los negativos.
Reducción: se dice que un elemento se reduce cuando gana electrones, aumentando sus
números de oxidación negativos y disminuyendo los positivos.
Las reacciones de oxidación-reducción pertenecen al tipo:
A + B
AB
o
AB + C
ABC
Siempre que participen en ellas algún elemento libre son reacciones redox.
El balanceo de ecuaciones químicas por el método redox conduce siempre al cálculo de
los estados de oxidación de las sustancias participantes. Para determinarlo se tendrá en
cuenta lo siguiente:
1. Se escribe la ecuación general no balanceada en forma tan completa como sea
posible.
2. Se asigna número de oxidación para observar qué experimentan cambios.
3.
- se dibuja un paréntesis para conectar a los átomos del elemento que se oxida. Se indica
el aumento del número de oxidación por átomo. Se dibuja un paréntesis para conectar a
los átomos del elemento que se reduce.
- se determinan los factores que igualan al incremento y la disminución total de
números de oxidación.
4. Se insertan coeficientes en la ecuación para igualar el incremento y la disminución de
npumeros de oxidación.
5. Se balancean los demás átomos por inspección.
3.2.2.- Por el método de ión electrón.
Por el método del ión-electrón.
En el método del ión-electrón se balancean las ecuaciones en forma separada y
completa describiendo semirreacciones de oxidación y de reducción. A continuación, se
iguala el número de electrones que se ganan y se pierden en ambas. Por último, se
suman las semirreacciones resultantes para obtener la ecuación total balanceada. De tal
forma se indica el procedimiento general.
1. Escriba la ecuación general sin balancear en forma tan completa como sea
posible.
2. Construya semirreacciones no balanceadas de oxidación y de reducción. Indique
fórmulas completas para iones y moléculas poliatómicas.
3. Balance por inspección todos los elementos de cada semirreacción con
excepción de H y O.
4. Balancee la carga de cada semirreacción añadiendo electrones en forma de
productos o reactivos.
5. Balancee la transferencia de electrones multiplicando las semirreacciones
balanceadas por los enteros adecuados.
6. Sume las semirreacciones resultantes y elimine los términos comunes para
obtener la ecuación balanceada.
I2 + S2O3-
I-
I2
I-
I2
2I-
I2 + 2e-
+
S4O62-
Semirreacción
reducción
2I-
Ecuación simple
de
Ecuación
balanceada
S2O32-
S4O62- Semirreacción
oxidación
2S2O32-
S4O62-
S2O32I2
+ 2e-
S2O32I2
+ S2O3-
de
S4O62- + 2e- Semirreacción
balanceada
2IS4O62- + 2eI-
+
S4O62-
Ecuación balanceada por el método ión-electrón.
de
oxidación
3.3.- Concepto de estequiometría.
Concepto de estequiometría.
La palabra estequiometría se deriva del girego stoicheion, que significa primer principio
o elemento, y metron, que quiere decir medida. La estequiometrpia describe las
relaciones cuantitativas entre los elementos en los compuestos (composición
estequiométrica) y entre las sustancias cuando experimentan cambios químicos
(estequiometría de reacción).
3.4.1.- Ley de la conservación de la materia.
Ley de la conservación de la materia.
No se produce cambio detectable en la cantidad de materia durante una reacción
química ordinaria. Este principio básico es la ley de la conservación de la materia, y
constituye la base para el balanceo de las ecuaciones químicas y los cálculos que se
realizan a partir de dichas ecuaciones.
3.4.2.- Ley de las proporciones constantes.
Ley de las proporciones constantes.
Diferentes muestras puras de un compuesto siempre contienen los mismos elementos en
las mismas proporciones de masa. Esta ley por lo general se le atribuye a Joseph Proust,
químico francés que la publicó en 1799. La ley dice si, por ejemplo, se analizan
muestras del gas de dióxido de carbono (CO2) obtenidos de fuentes diferentes, se
encontrará en cada una de las muestras la misma relación en masa entre carbono y
oxígeno.
3.4.3.- Ley de las proporciones múltiples.
Ley de las proporciones múltiples.
La cual establece que si dos elementos se pueden combinar para formar más de un
compuesto, las masas de un elemento que se combinan con la masa fija de otro
elemento se encuentran en relaciones de números enteros pequeños.
3.5.- Cálculos estequiométricos A.
3.5.1.- Unidades de medida usuales: átomo-gramo, mol-gramo, volumen-gramo
molecular, número de Avogadro.
Átomo gramo
Es el peso atómico de un elemento expresado en gramos. Como casi todos los
elementos se encuentran como mezclas de isótopos, los pesos átomo-gramo no suelen
ser números enteros; pero en muchos casos se aproximan a números enteros porque
predomina un isótopo sobre los demás.
Mol- gramo.
El peso molécula gramo (llamado molécula gramo o simplemente mol) es el peso
molecular expresado en gramos. Así 1 mol de CH4 pesa 16 g.
Volumen gramo molecular.
El volumen que ocupa 1 mol de cualquier gas a temperatura y presión normales (0C Y 1
atm.) está determinado por la ecuación del estado gaseoso:
PV = nRT
Donde:
V = volumen
P = presión
n = número de moles
R = constante de proporcionalidad
Número de Avogadro.
Avogadro establecio que: en condiciones iguales de presión y temperatura, volúmenes
iguales de cualquier gas, contienen el mismo número de moléculas.
La hipótesis de Avogadro permitió encontrar una escala para la masa atómicas, donde
un mol de un gas a 0oC y 1 atmósfera de presión, contienen 6.022 x 1023 moléculas,
independientemente del gas que se trate.
3.6.- Cálculos estequiométricos B: relación peso-peso, relación peso-volumen.
3.6.1.- Reactivo limitante, reactivo en exceso, grado de conversión o
rendimiento.
Estequiometría peso-peso.
Es el cálculo de los cambios de peso derivados de las relaciones molares
establecidas, constituye un procedimiento sumamente útil. Capacita al químico para
calcular las cantidades de reactivos necesarios para fabricar una cantidad determinada
de una nueva sustancia, facilita igualmente al biólogo molecular un procedimiento
cuantitativo para estudiar los procesos químicos que se cumplen en los organismos
vivientes. Igualmente permite al ingeniero calcular un proceso piloto destinado a la
economía de una operación industrial.
Las ecuaciones químicas no siempre son sencillas, y los cálculos peso/peso
basados en una sencilla ecuación balanceada frecuentemente representa situaciones
simplemente ideales. Pero aún en tales casos las estequiometría peso-peso suministra
información muy útil, la de las cantidades teóricas de las sustancias afectadas. Cuando
se combinan con datos de experimentación llevada a cabo, los cálculos teóricos
descubren o muestran la eficiencia de los procesos químicos.
Cuando un químico efectúa una reacción, los reactivos comúnmente no están
presentes en las cantidades estequiométricas exactas, esto es, en las proporciones
indicadas en la ecuación balanceada. El reactivo que se consume primero en la reacción
se llama reactivo limitante, dado que la máxima cantidad de producto formado depende
de la cantidad de este reactivo que se encuentra presente originalmente. Cuando se
acaba este reactivo, no se puede formar más producto. Los otros reactivos, presentes en
cantidades mayores que aquellas requeridas para reaccionar con la cantidad de reactivo
limitante presente, se llama reactivos excedentes.
La cantidad de reactivo limitante presente al inicio de la reacción está relacionada con la
cantidad de producto que se puede obtener de la reacción. Esta cantidad se llama
rendimiento de la reacción. Hay tres tipos de rendimientos relacionados con el estudio
cuantitativo de las reacciones químicas:
El rendimiento teórico de una reacción es la cantidad de producto que se predice
mediante la ecuación balanceada cuando ha reaccionado todo el reactivo limitante. El
rendimiento teórico es el rendimiento máximo que se puede obtener. En la práctica, la
cantidad de producto que se obtiene, llamado rendimiento real, es casi siempre inferior
al rendimiento teórico. Los químicos usan a menudo el término rendimiento
porcentual (% de rendimiento) , el cual describe la proporción del rendimiento real con
respecto al rendimiento teórico, y se define como sigue:
% de rendimiento = (rendimiento real / rendimiento teórico)
UNIDAD
4.-
ESTADO
LÍQUIDO,
SOLUCIONES,
SUSPENSIONES
Y
COLOIDES.
4.1.- Estado líquido.
Características del estado líquido
A nivel microscópico el estado líquido se caracteriza porque la distancia entre
las moléculas es sensiblemente inferior a la de los gases. Mientras que en un
gas la distancia intermolecular media es igual o mayor que diez veces el
tamaño de la molécula, en un líquido viene a ser del mismo orden de
magnitud que el diámetro molecular, y sólo un poco mayor que en los
sólidos. Eso explica que la densidad de los líquidos sea, salvo algunas
excepciones, sólo algo inferior a la de los sólidos.
La proximidad entre las moléculas hace que se dejen sentir fuerzas atractivas
de interacción, que evitan que una molécula pueda «escaparse» de la
influencia del resto, como sucede en el estado gaseoso, pero que les permite
moverse deslizándose unas sobre otras. Por esta razón los líquidos no
poseen forma propia, sino que se adaptan a la del recipiente que los
contiene, es decir, pueden fluir. Sin embargo, el hecho de que las moléculas
estén ya suficientemente próximas hace de los líquidos fluidos
incompresibles. Toda compresión lleva consigo una disminución de la
distancia intermolecular, y si ésta fuera apreciable entrarían en juego las
fuerzas repulsivas entre los núcleos atómicos que se opondrían a dicha
compresión y la neutralizarían.
Viscosidad
Aunque las moléculas de los líquidos pueden deslizarse unas sobre otras,
esto no sucede para todos con igual facilidad. La existencia de fuerzas de
rozamiento que se oponen al deslizamiento de las moléculas define una
propiedad de los fluidos que se denomina viscosidad. La viscosidad se
traduce en una mayor resistencia al movimiento en el interior del fluido. Así
un frasco de aceite es más difícil de agitar que uno de agua porque el aceite
es más viscoso que el agua. Los líquidos ideales carecen de viscosidad. En
los reales, la viscosidad varía de unos a otros, siendo extrema en los líquidos
superviscosos, también llamados sólidos amorfos, porque a la temperatura
ambiente presentan el aspecto de sólidos sin que la ordenación interna de
sus moléculas corresponda a la que es característica de los sólidos
cristalinos.
El vidrio constituye un ejemplo de este estado intermedio de la materia.
Aumentando la temperatura, disminuye su viscosidad y el material se
reblandece, pasando a un estado líquido espeso. El alquitrán que se utiliza
en el asfaltado de carreteras es otro ejemplo de sólido amorfo; en verano, al
aumentar la temperatura, se llega a deformar por efecto de la presión que
ejercen, sobre el firme, los vehículos pesados.
Tensión superficial y capilaridad
Todos los líquidos presentan una cierta tendencia a disminuir su superficie
libre, la cual se comporta de forma parecida a como lo hace una membrana
elástica. Dicha propiedad es debida a la existencia de fuerzas tangenciales a
la superficie o fuerzas de tensión, por lo que se denomina tensión superficial.
La tensión superficial se pone de manifiesto en multitud de fenómenos; así
cuando se sumerge un alambre circular en una solución jabonosa se forma
una película que recuerda a simple vista la membrana de un tambor, pues se
recupera de pequeñas deformaciones; si sobre la película de líquido se
deposita cuidadosamente un hilo cerrado, y se elimina la parte interior de la
película, se observa cómo el hilo se extiende hasta alcanzar la forma de una
circunferencia.
Una aguja de acero, engrasada simplemente por el tacto, puede flotar en el
agua y, del mismo modo, los patos se mantienen en la superficie de un lago
sin necesidad de nadar; en ambos casos los cuerpos son más densos que el
agua, a pesar de lo cual flotan.
Esta aparente contradicción con respecto a lo que establecen las leyes de la
hidrostática, se explica como debida al fenómeno de la tensión superficial
que convierte la superficie del líquido en una especie de malla tensa que
neutraliza las fuerzas del peso.
Desde un punto de vista molecular, la tensión superficial se explica como
debida a la condición especial de las moléculas situadas en la superficie del
líquido. Una molécula del líquido situada en el interior del mismo es solicitada
en todas direcciones por fuerzas atractivas procedentes de las otras
moléculas que la rodean, de modo que, por simetría, se compensan
mutuamente sus efectos.
En la superficie o en sus proximidades, la simetría se rompe y sólo las
moléculas que están por debajo de la superficie atraen a las de la capa
límite, dando lugar a una fuerza neta dirigida hacia el interior de la masa
líquida que tensa la superficie libre y produce ese efecto de malla o
membrana elástica.
La tensión superficial de un líquido viene expresada por su correspondiente
coeficiente de tensión superficial , que representa el trabajo necesario para
incrementar en una unidad la superficie libre del líquido o, en términos
equivalentes, la fuerza tangencial por unidad de longitud.
Cuando un tubo delgado de vidrio o capilar se introduce en agua situando su
extremo inferior por debajo de la superficie límite, el líquido asciende por su
interior hasta alcanzar una cierta altura de equilibrio. En este fenómeno
conocido como capilaridad el principio de los vasos comunicantes deja de
tener validez porque junto con las fuerzas del peso y de la presión
atmosférica interviene la tensión superficial.
Razonando en términos de equilibrio es posible encontrar una expresión para
la altura de la columna de líquido. Dado que el coeficiente de tensión
superficial representa la fuerza de tensión superficial por unidad de longitud,
la resultante de estas fuerzas responsables de la elevación de la columna
será:
T=2R 
siendo 2R la longitud del borde circular de la superficie libre. Por otra parte,
el peso de la columna viene dado por:
P = m · g = volumen ·  · g = R2hg
en donde  representa la densidad y h la altura.
Dado que las fuerzas de tensión superficial forman, en general, un ángulo 
de contacto con las paredes del capilar, la condición de equilibrio se
expresará en la forma:
T cos = P
es decir:
2Rcos = R2hg
y por tanto:
Esta expresión constituye la llamada Ley de Jurin e indica que la altura de la
columna líquida es directamente proporcional a la tensión superficial o del
líquido e inversamente proporcional al radio R del tubo. Para un cierto
número de líquidos, entre ellos el agua, puede considerarse en primera
aproximación que el ángulo de contacto  es igual a cero, con lo cual la
anterior ecuación se simplifica en la forma:
expresión que permite estimar el valor de  de un líquido, de densidad
conocida, midiendo h y R.
4.3.4.- Tixotropía.
La tixotropía se define como el fenómeno consistente en la pérdida de resistencia de un
coloide, al amasarlo, y su posterior recuperación con el tiempo. Las arcillas tixotrópicas
cuando son amasadas se convierten en un verdadero líquido. Si, a continuación, se las
deja en reposo recuperan la cohesión, así como el comportamiento sólido. Para que una
arcilla tixotrópica muestre este especial comportamiento deberá poseer un contenido en
agua próximo a su límite líquido. Por el contrario, en torno a su límite plástico no existe
posibilidad
de
comportamiento
tixotrópico.
TIXOTROPÍA: Es la propiedad de un material que le permite endurecerse en un
tiempo relativamente corto al estar en reposo, pero, por manipulación o
agitación, cambiar a una consistencia muy blanda o a un líquido de elevada
viscosidad, siendo el proceso completamente reversible.
UNIDAD 5.- GASES.
5.1.- Conceptos básicos: gas como estado de agregación, gas ideal, gas real,
propiedades críticas y factor de compresibilidad.
EL ESTADO GASEOSO
Las experiencias de Boyle
El estudio de los gases, y en particular del aire, atrajo la atención de los
físicos del siglo XVII y más concretamente la del irlandés Robert Boyle (16271691). Las experiencias que le permitieron establecer su conocida ley
consistieron, básicamente, en añadir mercurio a un tubo acodado
suficientemente largo abierto por un extremo y provisto de una llave en el
otro. Con la llave abierta vertía mercurio y su nivel en las dos ramas del tubo
se igualaba (principio de los vasos comunicantes). A continuación cerraba la
llave y añadía sucesivamente cantidades de mercurio iguales, con lo cual, la
presión a la que estaba sometido el gas encerrado en el otro extremo del
tubo, aumentaba en igual proporción. Mediante sucesivas medidas de la
distancia entre los dos niveles alcanzados por el mercurio en ambas ramas
del tubo, observó que la disminución del volumen del gas guardaba cierta
relación con el aumento de presión. Si doblaba el peso de mercurio, el
volumen se reducía a la mitad, si lo triplicaba se reducía a la tercera parte y
así sucesivamente. Un análisis cuidadoso de tales resultados experimentales
le permitió, finalmente, enunciar su ley.
Aun cuando Boyle no indicó explícitamente que la temperatura debía
permanecer constante durante el experimento, el descubrimiento
independiente efectuado por el físico francés Edme Mariotte (1630-1684) lo
puso de manifiesto, completando así las conclusiones del irlandés. A
temperatura constante, el volumen de un gas es inversamente proporcional a
la presión que soporta:
P · V = cte
para T = cte
(20.1)
Este enunciado constituye la llamada ley de Boyle-Mariotte.
Algunas investigaciones históricas recientes han puesto de manifiesto que,
en la interpretación de sus datos experimentales, Boyle dispuso de una
importante ayuda: la lectura de un artículo en el que dos científicos
británicos, Henry Power y Richard Towneley proponía la relación PV =
constante. El propio Boyle lo reconoció en su día públicamente sin pretender
atribuirse la originalidad del descubrimiento, sin embargo, la historia sí que lo
hizo, ignorando injustamente la aportación de Power y Towneley al estudio
de los gases.
Las leyes de Gay-Lussac
El estudio de la dilatación de los gases puede efectuarse con la ayuda de un
matraz de vidrio que termine en un tubo capilar acodado por cuyo interior
puede deslizarse un índice de mercurio sobre una escala graduada. La
dilatación de la sustancia gaseosa contenida en el recipiente, puede
observarse, de forma controlada, sumergiendo el matraz en un baño de agua
cuya temperatura puede variarse a voluntad. La lectura del volumen del gas
sobre la escala graduada y de la temperatura del agua sobre un termómetro
empleado al efecto, permite encontrar una relación entre ambas magnitudes
físicas en condiciones de presión constante e igual a la presión atmosférica.
Experimentos de este tipo llevaron al químico francés Joseph Louis GayLussac (1778-1850) a concluir que, a presión constante, el volumen de un
gas aumenta proporcionalmente al incremento de temperatura, siendo la
constante de proporcionalidad la misma para todos los gases. Este
enunciado, que se conoce como primera Ley de Gay-Lussac, se expresa
matemáticamente mediante la ecuación:
Vt = V0 (1 + t)
(20.2)
donde Vt representa el volumen a la temperatura de t ºC, V0 el volumen a 0
ºC y  es una constante aproximadamente igual para todos los gases que se
denomina coeficiente de dilatación y cuyo valor es:  = 1/273. El que  sea
igual a 1/273 significa que cuando la temperatura de un gas se eleva en un
grado centígrado, su volumen aumenta 1/273 veces el volumen inicial, es
decir, se dilata en un
0,37 % por grado centígrado.
La primera ley de Gay-Lussac se conoce también como ley de Charles-Gay
Lussac, ya que fue sugerida con anterioridad en una forma semejante por
Jacques Charles (1746-1823).
Experiencias semejantes realizadas manteniendo constante el volumen y
estudiando la variación de la presión con la temperatura permitieron al
químico francés establecer la que se conoce como segunda Ley de Gay
Lussac: a volumen constante, la presión de un gas aumenta
proporcionalmente al incremento de temperatura, siendo la constante de
proporcionalidad la misma para todos los gases.
Este enunciado, semejante al de la primera ley, se expresa mediante una
ecuación similar en la forma:
Pt = P0 (1 + t)
(20.3)
siendo  el coeficiente de compresibilidad a volumen constante,
aproximadamente igual para todos los gases y cuyo valor es  = 1/273.
La ley de los gases perfectos
Las leyes de Boyle-Mariotte y de Gay-Lussac sobre el comportamiento de los
gases, aunque son aplicables dentro de una buena aproximación a los gases
existentes en la naturaleza, son tanto más imprecisas cuanto mayor es la
densidad, la presión o la temperatura del gas. Por ello los gases que cumplen
con exactitud dichas leyes físicas se denominan gases perfectos o ideales.
Es posible combinar las leyes de los gases en una sola ecuación sencilla si la
temperatura se expresa en la escala absoluta o Kelvin. Así la ley de CharlesGay Lussac puede escribirse como:
V = kT
Operando en la ecuación (20.2) se tiene:
V = V0 (1 + t) =
y como 273 + t(ºC) = T(K), expresando la temperatura en Kelvin resulta, en
efecto:
Por otra parte la ley de Boyle establece la proporcionalidad inversa entre V y
P, es decir:
Combinando ambas relaciones de proporcionalidad se tiene:
o lo que es lo mismo:
que indica que el producto del volumen de un gas por su presión dividido por
su temperatura absoluta es una cantidad constante. Ello significa que una
muestra gaseosa dada puede evolucionar de un estado inicial a otro final
cambiando en el proceso su presión, su volumen o su temperatura, pero
siempre que la cantidad PV/T no varíe.
La ecuación (20.4) constituye una expresión de la llamada ley de los gases
ideales o perfectos, que también se conoce como ecuación de estado. Para
dos estados cualesquiera inicial y final las magnitudes P, V y T están
relacionadas en la forma:
La constante de proporcionalidad depende de la cantidad de sustancia
gaseosa considerada. Cuando esta circunstancia se introduce en la ecuación
(20.4) resulta la expresión de la ley de los gases ideales más usada:
PV=nRT
(20.5)
donde n es el número de moles de la muestra gaseosa considerada y R es la
llamada constante de los gases perfectos igual a:
0,082 atm · 1/K · mol.
La teoría cinética: una explicación para las leyes de los gases
Las experiencias de Boyle y de otros físicos de la época pusieron claramente
de manifiesto que los gases podían comprimirse y expandirse. Pero, ¿cómo
explicar estas propiedades que los diferenciaban claramente de los líquidos y
los sólidos? Las ideas de los atomistas griegos influyeron en Boyle de tal
manera que propuso dos explicaciones alternativas para el comportamiento
de los gases basadas ambas en la hipótesis de que la materia estaba
compuesta de partículas indivisibles o átomos.
La primera partía del supuesto de que los átomos estaban en reposo y en
contacto mutuo, y explicaba la compresibilidad como consecuencia de una
cierta elasticidad de los átomos que podrían comportarse como una especie
de muelles blandos. Este modelo estático, sin embargo, no podía explicar la
expansibilidad ilimitada de los gases. En cambio, si los átomos no estuvieran
ni en reposo ni en contacto mutuo entonces podrían desplazarse
rápidamente de un lado a otro en el interior del recipiente, llenando así todo
el espacio.
Las ideas tímidamente expuestas por Boyle respecto de la posibilidad de un
modelo cinético fueron desarrolladas por el físico suizo Daniel Bernouilli
(1700-1782). Según Bernouilli los átomos o corpúsculos de gas, debido a su
pequeño tamaño, se encontraban en un enorme número aun en pequeños
volúmenes gaseosos. Su movimiento incesante producía choques entre sí y
con las paredes del recipiente. Esta innumerable cantidad de impactos de los
corpúsculos gaseosos explicaba el efecto observable de la presión del gas y,
por tanto, su expansibilidad.
De acuerdo con sus razonamientos, la disminución del volumen del gas
restringe el recorrido de los corpúsculos móviles y por tanto, incrementa el
número de choques por segundo contra las paredes del recipiente, esto es,
aumenta la presión del gas. Estudios teóricos apropiados permitieron a
Bernouilli deducir, matemáticamente, la ley de Boyle a partir de estas
sencillas ideas. Junto con la explicación del por qué de la ley de Boyle, la
teoría cinética de los gases logró, asimismo, la explicación de las leyes de
Gay-Lussac.
Además, a partir del significado de la presión del gas según el modelo
cinético y de la segunda ley de Gay-Lussac, fue posible encontrar un
significado también cinético a la magnitud temperatura. Así cuanto mayor es
la temperatura de un gas tanto mayor es la presión que ejerce, es decir, más
enérgicos deben ser los impactos de las partículas del gas sobre el interior
del recipiente. Estudios más rigurosos desarrollaron esta idea sencilla
sugerida por el físico alemán Rudolph Clausius (1822-1888) y permitieron
establecer que la temperatura absoluta de un gas constituye una medida de
la energía cinética media de las moléculas del gas en su movimiento de
agitación desordenada.
La extensión de la teoría cinética a otros estados de agregación de la materia
ha permitido comprender los fenómenos de cambio de estado desde un
punto de vista molecular.
APLICACIÓN DE LA ECUACIÓN DE ESTADO DE LOS GASES
Una cierta masa de nitrógeno ocupa 10 litros a 1 atm de presión y 27 ºC de
temperatura. ¿Qué volumen ocupará la misma masa de gas si las condiciones
cambian a 2 atm y 207 ºC? ¿Cuál sería la presión del gas si las condiciones
finales de volumen y temperatura fueran de 20 litros y 27 ºC?
La relación entre los valores de las magnitudes P, V y T de un gas en un
estado inicial y otro final puede encontrarse aplicando correctamente la
ecuación de estado. En todo caso, es preciso recordar que la T que aparece en
ella es temperatura absoluta. Si se designa con el subíndice 0 el estado inicial y
con el 1 el estado que corresponde a las condiciones de la primera pregunta
del problema, se tendrá entonces:
en donde
P0 = 1 atm
V0 = 10 litros
T0 = 27 + 273 = 300 K
P1 = 2 atm
T1 = 207 + 273 = 480 K
luego despejando V1 resulta:
Análogamente y designando con el subíndice 2 el estado que corresponde a
las condiciones de la segunda pregunta, resulta:
siendo V2 = 20 litros y T2 = T0 = 300 K. Luego:
En este caso la transformación se ha efectuado a T = cte, es decir, en las
condiciones que recoge la ley de Boyle.
5.2.- Propiedades PVT: Ley de Boyle, Charles, Gay-Lussac.
En 1662 Robert Boyle observó la relación que existía entre la presión de un gas
y su volumen, manteniendo la temperatura constante. De las observaciones
que
realizó,
concluyó
lo
siguiente:
"Al aumentar la presión de un sistema, su volumen disminuye". Este hecho
puede expresarse matemáticamente en la siguiente forma:
En
donde:
P
=
V = volumen del mismo
presión
del
sistema
La ecuación (1) se puede expresar también así:
En donde K = constante de proporcionalidad
Para cambiar un estado 1, al estado 2, podemos escribir:
En donde:
P1
=
presión
V1
=
volumen
P2
=
presión
V2 = volumen final del sistema
inicial
inicial
final
del
del
del
sistema
sistema
sistema
El valor de la constante de proporcionalidad depende de: la temperatura a la
que se trabaja, la masa del gas, la naturaleza del mismo y las unidades en que
se
expresan
la
presión
y
el
volumen.
Al observar las ecuaciones obtenidas se verá que corresponden a la de una
hipérbola equilátera. La representación gráfica de las mismas en una gráfica
presión vs volumen tendrá la siguiente forma:
Figura 1
A este tipo de curvas se les conoce con el nombre de isotermas.
Debido a que es más cómodo trabajar con gráficas que correspondan a una
línea recta, es común construir gráficas de producto PV vs. V en lugar de las
anteriores:
Figura 2
TECNICA
Este experimento se realiza empleando el equipo de la siguiente figura. Aquí el
sistema debe permanecer a temperatura constante y se harán variaciones del
volumen del gas que se encuentra encerrado en el tubo de la derecha,
moviendo el tubo de la izquierda de arriba hacia abajo o viceversa, y el desnivel
del mercurio leído en el papel milimétrico nos dará la presión manométrica a la
que se encuentra el gas. Para cada volumen, nuevamente se elabora una tabla
de datos de volumen y presión manométrica, cuidando que cada lectura se
realice después de dejar que el sistema gaseoso equilibre su temperatura con
la ambiente. Se recomienda que se dejen 5 minutos para lograr el equilibrio
térmico.
CALCULOS
Hacer una gráfica de presión vs volumen y trazar la isoterma.
Jacques Charles y Joseph-Louis Gay-Lussac, a comienzos de 1800,
estudiaron con detalle qué relaciones existían entre la temperatura de
los gases y el volumen que ocupaban. La moda de volar en globos
aerostáticos fue un incentivo importante en sus investigaciones.
Se encierra un gas en una de las ramas de un tubo en U. Este
manómetro de "gas comprimido" se introduce en un baño de agua;
se va midiendo el volumen que ocupa según se varía la temperatura
del agua (que es la del gas).
Químico y físico francés, nacido el 6 de diciembre de 1778, en Saint-Léonardde-Noblat, y muerto el 9 de mayo de 1850, en París. Estudió en la école
Polytecnique y en la école des Ponts et Chaussées de París.
Además de ocupar cargos políticos de importancia, Gay-Lussac fue catedrático
de física (a partir de 1808) en la universidad de la Sorbona, así como
catedrático de química (a partir de 1809) en el Politécnico de París.
Estudió las propiedades físicas y químicas de los gases y descubrió, en 1802 y
1820, las leyes que llevan su nombre, sobre la dilatación térmica y, entre 18051808, las referidas a las relaciones entre los volúmenes de los gases que
forman compuestos.
En 1809 formuló la ley de los gases que sigue asociada a su nombre. La ley de
Gay-Lussac de los volúmenes de combinación afirma que los volúmenes de los
gases que intervienen en una reacción química (tanto de reactivos como de
productos) están en la proporción de números enteros pequeños.
En relación con estos estudios, investigó junto con el naturalista alemán
Alexander von Humboldt, la composición del agua, descubriendo que se
compone de dos partes de hidrógeno por una de oxígeno. Unos años antes,
Gay-Lussac había formulado una ley, independientemente del físico francés
Jacques Alexandre Charles, que afirmaba que el volumen de un gas es
directamente proporcional a su temperatura absoluta si la presión se mantiene
constante; hoy se conoce como ley de Charles y Gay-Lussac.
En 1811 el químico francés Courtois, por medio de una reacción química
produjo un gas violeta que Gay-Lussac identificó como un nuevo elemento y le
dio el nombre de yodo, que en griego significa violeta.
Estudió también el ácido cianhídrico así como el gas de hulla. En el año 1835
creó un procedimiento para la producción de ácido sulfúrico basado en el
empleo de la torre llamada de Gay-Lussac.
Gracias a sus mediciones químicas de precisión y a sus procedimientos
exactos de trabajo, logró obtener varios elementos químicos y establecer las
bases del análisis volumétrico convirtiéndolo en una disciplina independiente.
En el campo de la física llevó a cabo, en 1804, dos ascensiones en globo,
hasta altitudes de 7.000 metros, durante las que estudió la composición de las
capas altas de la atmósfera y el magnetismo terrestre.
En la lucha de prestigio entre Francia e Inglaterra,
Napoleón suministró fondos a Gay-Lussac para que construyera una batería
eléctrica mayor que la de Davy, y así encontrar nuevos elementos.
La batería no fue necesaria, pues Gay-Lussac y Thenard empleando el potasio
descubierto por Davy, aislaron el boro sin necesidad de la electricidad. Al tratar
óxido de boro con potasio se produjo el elemento boro.
En 1809 Gay-Lussac trabajó en la preparación del potasio e investigó las
propiedades del cloro. En el campo de la industria química desarrolló mejoras
en varios procesos de fabricación y ensayo.
En 1831 fue elegido miembro de la Cámara de los Diputados y en 1839 del
Senado.
UNIDAD 6.- TERMOQUÍMICA Y ELECTROQUÍMICA.
6.1.- Termoquímica.
La termoquímica es una metodología de investigación utilizada desde la época de
Lavoisier y Berthelot, quienes desarrollaron instrumentos de medición de alta precisión
y belleza, para conocer esencialmente el así llamado “poder calorífico”. Mas tarde esta
metodología cubrió áreas de investigación no sólo de química sino también de biología.
Con el paso de los años adquirió una mayor fundamentación y apego a lo establecido
por la termodinámica, de manera que los resultados obtenidos a través de ella pueden
usarse para encontrar información de suficiente calidad como para asociarla a la
estructura de las moléculas.
6.1.2.- Calor de formación.
El calor de formación Hf de una sustancia química representa la energía
liberada o consumida durante la formación de dicha sustancia, en condiciones
normales, a partir de los elementos que la constituyen. Si en tales condiciones
se consideran nulos los contenidos energéticos H de los elementos, el calor de
formación Hf de un compuesto coincide con su contenido energético o
entalpía. Si se compara la definición de calor de formación con la de calor de
reacción se observa que el calor de formación es un tipo particular de calor de
reacción (el correspondiente a reacciones de formación o de síntesis de un
compuesto).
La determinación de calores de reacción puede efectuarse de un modo
experimental si la reacción correspondiente se lleva a cabo de forma aislada y
controlada en el interior de un calorímetro. Sin embargo, en ocasiones, esto no
es posible porque tienen lugar varias reacciones simultáneamente, y no una
sola. En tales casos es posible determinarlos de una forma indirecta,
recurriendo a una propiedad de la entalpía; el hecho de que H sea una función
de estado, esto es, que dependa exclusivamente de los estados inicial y final
del sistema, permite calcular calores de reacción a partir del conocimiento de
procesos intermedios.
6.2.- Electroquímica.
Electroquímica, parte de la ciencia química que reparte con la interrelación de corrientes
eléctricas, o voltajes y reacciones químicas, y con la conversión mutua de energía
química y eléctrica. En el sentido más ancho, electroquímica es el estudio de las
reacciones químicas que producen efectos eléctricos y de los fenómenos químicos que
son ocasionados por la acción de corrientes o los voltajes.
6.2.1.- Electroquímica y celdas electrolíticas.
La energía involucrada en el transporte de cargas que producen una corriente
eléctrica se puede emplear para efectuar una reacción particular que no se
produce espontáneamente. El dispositivo que permite efectuar esa reacción por
medio del paso de una corriente eléctrica se denomina celda electrolítica.
Las celdas electroquímicas son aquellas donde se producen reacciones de óxidoreducción. Cuando dicha reacción no se produce en forma espontánea, estamos en
presencia de una celda electrolítica y para que se produzca algún cambio en la misma,
es necesario entregar energía al sistema. En este caso, energía eléctrica proveniente del
medio exterior es convertida en energía química, permitiendo que una transformación
no espontánea pueda ocurrir.
6.2.2.- Electroquímica y celdas voltaicas (galvánicas).
Cuando una reacción química en la que hay cambio en los estados de
oxidación se produce espontáneamente, se puede diseñar un dispositivo que
permita el paso de las cargas por una región determinada constituyéndose en
una celda galvánica. En una celda galvánica se utiliza una reacción de oxidoreducción para generar una corriente eléctrica.
Una celda galvánica produce corriente eléctrica porque no se encuentra en
equilibrio. La reacción procede de manera espontánea hasta que se alcanza
ese estado de equilibrio.
El cabio de energía libre de Gibbs para una reacción en la que las especies
presentes se encuentran en solución y se genera una diferencia de potencial
que puede promover el transporte de partículas cargadas se expresa por medio
de la relación
en esta expresión E representa la diferencia de potencial eléctrico y nF es la
cantidad de carga que se puede transportar debido a esa diferencia de
potencial. En el marco de referencia de la termodinámica un proceso se realiza
espontáneamente cuando hay una reducción en la función energía libre de
Gibbs. De otra parte en desarrollo independiente la electroquímica definió la
partículas móviles responsables de la aparición de la corriente eléctrica como
transportando cargas eléctricas negativas. Con este definición y desde el
marco de referencia de la electroquímica un proceso se realiza
espontáneamente cuando esas cargas se mueven en un campo que debe
tener potencial positivo. La correspondencia inequívoca entre esos marcos de
referencia justifica la asignación del signo negativo en la expresión anterior.
Para cualquier reacción la expresión de la energía de Gibbs incluye un término
que involucra los contenidos energéticos de las especies presentes en sus
estados de referencia y otro término que involucra el cuociente entre las
cantidades de sustancia presentes en un caso particular.
En términos de los potenciales electroquímicos de las especies que sufren una
reacción de oxido-reducción la expresión anterior se transforma en:
Cuando se detiene la reacción porque el sistema ha alcanzado el equilibrio el
cambio de energía libre de Gibbs y el potencial se hacen iguales a cero y el
cuociente de concentraciones de las especies involucradas tiene el valor
correspondiente a la constante de equilibrio, entonces se obtiene:
6.2.4.- Corrosión.
La corrosión electroquímica es un proceso espontáneo que denota
siempre la existencia de una zona anódica (la que sufre la corrosión), una
zona catódica y un electrolito, y es imprescindible la existencia de estos tres
elementos, además de una buena unión eléctrica entre ánodos y cátodos, para
que este tipo de corrosión pueda tener lugar. La corrosión más frecuente
siempre es de naturaleza electroquímica y resulta de la formación sobre la
superficie metálica de multitud de zonas anódicas y catódicas; el electrolito
es, en caso de no estar sumergido o enterrado el metal, el agua condensada
de la atmósfera, para lo que la humedad relativa deberá ser del 70%.
El proceso de disolución de un metal en un ácido es igualmente un
proceso electroquímico. La infinidad de burbujas que aparecen sobre la
superficie metálica revela la existencia de infinitos cátodos, mientras que en
los ánodos se va disolviendo el metal. A simple vista es imposible distinguir
entre una zona anódica y una catódica, dada la naturaleza microscópica de
las mismas (micropilas galvánicas). Al cambiar continuamente de posición
las zonas anódicas y catódicas, llega un momento en que el metal se disuelve
totalmente.
Las reacciones que tienen lugar en las zonas anódicas y catódicas son las
siguientes:
ánodo: Me
Me n+ + ne+
cátodo: 2H + 2e H2
(medio ácido)
O2+2H2O
+
4e4OH-
(medio
alcalino)
neutro
(oxidación)
y}
(reducción)
Ya que la corrosión de los metales en ambientes húmedos es de
naturaleza electroquímica, una aproximación lógica para intentar parar la
corrosión sería mediante métodos electroquímicos. Los métodos
electroquímicos para la protección contra la corrosión requieren de un
cambio en el potencial del metal para prevenir o al menos disminuir su
disolución.
La protección catódica, en este sentido, es un tipo de protección
(electroquímico) contra la corrosión, en el cual el potencial del electrodo del
metal en cuestión se desplaza en la dirección negativa. Los principios de la
protección catódica pueden ilustrarse mediante un diagrama termodinámico
potencial - pH, como se muestra en la figura 10, en el caso del hierro (Fe).
Figura 10. Diagrama potencial -pH para el Hierro (Fe).
Consideremos un espécimen de acero al carbono sumergido en
ácido clorhídrico (HCl) de concentración 0.1 M. El acero se
disolverá con desprendimiento de hidrógeno (H2). El potencial
de corrosión del espécimen quedará entre los potenciales de
equilibrio correspondientes al electrodo de H2 y Fe (puntos A y
B en la figura 10).
De acuerdo con el diagrama, hay un camino para prevenir la
corrosión mediante un cambio de potencial. Aplicando una
corriente catódica, el potencial del espécimen de acero se
desplazará en la dirección negativa, hacia la zona de inmunidad,
en la cual el metal, termodinámicamente, se encuentra estable (no
se puede corroer). Para lograr este desplazamiento del potencial
en la dirección negativa, el objeto que se corroe se une
eléctricamente a un metal más negativo en la serie
electroquímica, un ánodo, formando una celda galvánica en la
que actuará como cátodo. Para que el metal esté protegido
catódicamente, el valor de su potencial de electrodo tiene que
quedar por debajo de su potencial de corrosión en la solución
mencionada. Su disolución será así prevenida totalmente
(protección catódica completa) o al menos disminuirá (protección
catódica incompleta). Como consecuencia de la corriente que
circule en la celda galvánica formada, en el metal protegido
catódicamente tendrá lugar el desprendimiento de hidrógeno o la
reducción de oxígeno.
UNIDAD 7.- EQUILIBRIO QUÍMICO, CINÉTICA QUÍMICA Y EQUILIBRIO EN
SOLUCIÓN.
7.1.- Cinética química: velocidades de reacción y el mecanismo de reacción.
Mecanismos de reacción
Desde el punto de vista termodinámico, en una reacción química, los reactivos
constituyen el estado inicial y los productos el estado final. Al pasar del estado
inicial al estado final, se produce un cambio de la energía libre. Cuando el
cambio es negativo se dice que la reacción es espontánea y no existe ningún
impedimento termodinámico para que la reacción se produzca, sin embargo este
enfoque sólo tiene en cuenta las propiedades de reactivos y productos aislados,
no incluye los posibles obstáculos que puedan existir durante la reacción.
Consideremos la siguiente reacción:
AB + C < = > A + BC
La formación del nuevo enlace B-C requiere que las moléculas de los reactivos
AB y C se acerquen a distancias lo suficientemente cortas para permitir un
solapamiento eficaz de sus orbitales. Sin embargo, la disminución de la distancia
comporta un aumento de la repulsión entre las nubes electrónicas. Para vencer la
repulsión, las moléculas de los reactivos deben acercarse con suficiente energía
cinética. Por encima de una determinada energía que permita el solapamiento
eficaz, se empezarán a formar los nuevos enlaces de los productos, a la vez que
se debilitarán los enlaces de los reactivos, formándose una especie integrada por
todas las moléculas de reactivos y en la cual unos enlaces se están rompiendo
mientras otros se están formando. Esta especie se conoce como complejo
activado. Finalmente, se acabaran de romper los enlaces de los reactivos para
conducir a la formación de los productos de la reacción. El proceso global se
puede esquematizar en la forma:
AB + C < = > A···B···C < = > A + BC
La figura siguiente muestra la variación de la energía en función de la
coordenada de reacción:
Puesto que para formar el complejo activado los reactivos deben vencer las
fuerzas de repulsión, la energía del complejo activado es más alta que las
energías de los reactivos y de los productos. La diferencia entre la energía de los
reactivos y la del complejo activado se denomina energía de activación, y puede
considerarse como una barrera energética que deben sobrepasar los reactivos
para transformarse en productos.
La reacción anterior se produce con la formación de un solo complejo activado y
superando una sola barrera de energía de activación. Este tipo de procesos se
llama reacciones elementales. Una reacción puede transcurrir también mediante
dos o más procesos elementales. En tal caso, diremos que la reacción es
compleja.
El número de moléculas que toman parte como reactivos en un proceso
elemental se denomina molecularidad. Se conocen reacciones elementales
unimoleculares, bimoleculares y trimoleculares, aunque estas últimas son muy
escasas. La descomposición del ozono nos proporciona un buen ejemplo de
reacción compleja, con una etapa unimolecular y dos etapas bimoleculares:
O3 < = > O2 + O
O3 + O
-->
2 O2
Sumando las etapas elementales se obtiene la reacción global:
2 O3 --> 3 O2
El conjunto de los procesos elementales de una reacción se denomina
mecanismo de reacción.
Ecuación de velocidad y orden de reacción
La extensión en la cual ha progresado una reacción se conoce como grado de
avance de la reacción, E, para reacciones a volumen constante puede definirse
como:
Ci (t) - Cio
E = ---------------
(1)
ri
En esta expresión Ci (t) es la concentración del componente i que hay en el
tiempo t, Cio la inicial y ri el coeficiente estequiométrico con su signo, positivo
para productos y negativo para reactivos. El grado de avance es independiente
de la especie que se mida, por ello la velocidad de reacción se puede definir
como la variación del grado de avance con el tiempo:
(2)
dt
Por ejemplo, en la reacción trimolecular:
A + 2 B --> 3 D
ri
d E
1
dCi (t)
------- = ------ . --------dt
la velocidad se puede expresar convenientemente como:
dCA
1
dCB
1 dCD
v = - ------- = - --- . ------- = --- . ------dt
2
dt
3
dt
(3)
La división por los coeficientes estequiométricos es necesaria para unificar el
concepto de velocidad de reacción, haciéndolo independiente de la especie
química considerada. Además, asegura que la velocidad de reacción sea siempre
positiva, tanto si se considera un reactivo como un producto.
La expresión que relaciona la velocidad de reacción con las concentraciones de
los compuestos que toman parte en ella denomina ley de velocidad o ecuación
de velocidad. En el caso de un proceso elemental, la velocidad es proporcional al
producto de las concentraciones de los reactivos elevadas a sus correspondientes
coeficientes estequiométricos. Dos ejemplos son:
A + B --> P
v = k [A] [B]
2A
-->
P
v = k [A] 2
La constante de proporcionalidad k se conoce como constante de velocidad o
cinética.
Para reacciones complejas, la ecuación de velocidad no es tan sencilla, y
depende del mecanismo de reacción. De todas formas, para muchas reacciones
la velocidad es proporcional a potencias de las concentraciones de los reactivos:
(4)
v = k [A] n [B] m
En la ecuación anterior, las potencias son los ordenes de reacción respecto a
cada uno de los reactivos. Así, n es el orden de reacción respecto a la especie A,
y m es el orden de reacción respecto a la especie B. La suma de todos los
ordenes de reacción, n + m + ..., se denomina orden global de la reacción. En los
procesos elementales los ordenes de reacción respecto a cada uno de los
reactivos coinciden con los respectivos coeficientes estequiométricos y el orden
global de la reacción coincide con su molecularidad.
Como ejemplo de reacción con una ley de velocidad sencilla se puede considerar
la reacción de iodo con el hidrógeno:
I2 + H2 --> 2 HI
En determinadas condiciones experimentales es un proceso elemental gobernado
por la ley de velocidad siguiente:
(5)
v = k [I2 ] [H2 ]
Según esto, esta reacción es de primer orden respecto al iodo y al hidrógeno, y
de segundo orden global. Además, al tratarse de un proceso elemental único
podemos afirmar que la molecularidad es dos y que la reacción es bimolecular.
En cambio, la ecuación de velocidad para la reacción compleja de
descomposición del ozono es:
[O3 ] 2
v = k ---------
(6)
[O2 ]
Un orden de reacción no tiene por que ser un número entero, sino que puede ser
un número fraccionario o incluso negativo. En estos casos, siempre se trata de
reacciones complejas. Un ejemplo es:
Br2 + H2
-->
2 HBr
[H2 ] [Br2 ] 3/2
v = k ----------------------[Br2 ] + k' [HBr]
Determinación experimental de la ecuación de velocidad
Cuando se aborda el estudio cinético de una reacción, el primer objetivo es
establecer la ecuación de velocidad. Lo cual supone la determinación de los
ordenes de reacción y de la constante de velocidad. Así, si se estudia una
reacción de la forma:
a A + b B --> P
como primera aproximación, podemos suponer una ley general del tipo:
(7)
v = k [A] n [B] m
Para determinar los ordenes de reacción se puede hacer uso del método de las
velocidades iniciales, el cual se basa en la medida de la velocidad inicial, vo,
para a diversas mezclas de reacción en las que se mantienen constantes todas las
concentraciones excepto una. En esas condiciones la velocidad aparece como
una función de la única concentración variable y, por lo tanto, se puede
determinar fácilmente el orden de reacción respecto a dicha especie. Así, en la
reacción anterior, para determinar n se mantendría constante la concentración de
B y se haría uso de la expresión:
(8)
vo = k' [A] on
donde k' incluye el término constante de concentración de B. Tomando
logaritmos resulta:
(9)
log vo = log k' + n log [A] o
que es la ecuación de una recta. Una serie de experiencias realizada para
diversas concentraciones iniciales de A nos permitirá obtener diversos puntos de
la recta. El orden de reacción, n, es la pendiente de la recta, que puede obtenerse
ajustando por mínimos cuadrados.
Experimentalmente, la determinación de la velocidad inicial se lleva a cabo
tomando medidas de la concentración dentro de un intervalo de tiempo
suficientemente pequeño al comienzo de la reacción. Así por ejemplo, si se
toman una serie de medidas de la concentración de A a diferentes valores del
tiempo t desde el instante inicial donde t = 0, la velocidad inicial se puede
calcular como:
1
[A] t - [A] o
v o= --- . ---------------
(10)
a
t
Las series de medidas de vo permitirán calcular el orden de reacción respecto a
A. Las medidas de la concentración del reactivo se toman haciendo uso de un
método analítico suficientemente sensible, rápido y selectivo. Usualmente se
emplea un método basado en la medida de una propiedad física proporcional a la
concentración de la especie de interés, tal como la absorbancia, o el potencial de
un electrodo selectivo.
Una vez determinado el orden de la reacción respecto a una especie, se procede
a determinar el orden respecto a otra y así sucesivamente. En el caso de
reacciones complejas es necesario estudiar el orden de reacción respecto a las
concentraciones de los productos, puesto que en numerosas ocasiones también
están incluidos en la ley de velocidad. Cuando se conocen todos los ordenes se
puede determinar la constante de velocidad de la forma:
vo
k = -----------------
(11)
[A]on [B]om
Alternativamente se puede ajustar la recta:
(12)
log vo = log k + log ( [A] on [B] om )
y obtener k de la ordenada en el origen.
Integración de leyes de velocidad sencillas
Reacciones de orden cero: En este caso la velocidad de formación del producto
viene dada por una ecuación del tipo:
d [P]
-------- = k
(13)
dt
cuya integración conduce a:
(14)
[P] = [P] o + k t
y por tanto a una variación lineal de la concentración con el tiempo. Reacciones
de orden cero se encuentran frecuentemente en catálisis heterogénea, cuando la
reacción se lleva a cabo sobre una superficie saturada de reactivo. Y en
reacciones catalizadas con suficiente exceso de substrato para saturar el
catalizador.
Reacciones de
unimoleculares:
A
-->
primer
orden:
Corresponden
a
procesos
elementales
P
La ley de velocidad es del tipo:
d[A]
-------- = - k [A]
(15)
dt
La integración de esta ecuación conduce a una expresión logarítmica:
(16)
ln [A] = - k t + ln [A] o
Representando ln [A] frente al tiempo se obtiene una recta de pendiente igual a k y con ordenada en el origen igual a ln [A]o. En procesos gobernados por leyes
de primer orden la concentración de reactivo, A, disminuye exponencialmente y,
de manera simultánea, la concentración de producto aumenta también
exponencialmente:
(17)
(18)
[A] = [A] o e
[P] = [A] o (1 - e
-kt
- k t
)
Un concepto importante en cinética es el tiempo de vida media o período de
semireacción. Se define como el tiempo necesario para que la concentración del
reactivo se reduzca a la mitad. En el caso de una reacción de primer orden
resulta:
(19)
[A] o / 2 = [A]o e - k t1/2
y por tanto, la vida media viene dada por:
(20)
t1/2 = ( ln 2) / k
Algunos ejemplos de reacciones de primer orden son:
 La desintegración de un isótopo radiactivo:
Ra --> Rn +
 La isomerización del ciclopropano:
(CH2 ) 3 --> CH 3 - CH=CH 2
 Finalmente, la descomposición del pentóxido de dinitrógeno:
2 N2 O5 --> 4 NO2 + O2
que es una reacción compleja, pero que globalmente sigue una cinética de
primer orden.
Reacciones de segundo orden: Pueden darse dos casos, dependiendo de que la
ecuación de velocidad sea función de la concentración de un solo reactivo o de
dos. El primer caso corresponde a una reacción elemental del tipo:
2A
-->
P
que podrá describirse mediante la ecuación de velocidad de segundo orden
siguiente:
d[A]
-------- = - k [A] 2
(21)
dt
La integración de esta ley de velocidad conduce a:
(22)
1 / [A] = k t + 1 / [A] o
y por tanto, la representación de 1/[A] frente al tiempo da lugar a una recta de
pendiente k y ordenada en el origen 1/[A]o. La concentración de A experimenta
una variación hiperbólica con el tiempo:
(23)
[A] = [A] o / (1 + [A] o k t )
El tiempo de vida media para este tipo de reacciones tiene la expresión:
(24)
t1/2 = 1 /( [A] o k )
El otro tipo de reacción de segundo orden viene representado por el proceso
elemental:
A + R --> P
que esta gobernado por la ecuación de velocidad:
d[A]
-------- = - k [A] [R]
(25)
dt
si llamamos x a la concentración de A que ha reaccionado en el tiempo t, la ley
de velocidad integrada será:
(26)
1
[R]o ( [A]o - x )
-------------- ln ----------------------- = - k t
[R]o - [A]o
[A]o ( [R]o - x )
Un caso particular importante se encuentra cuando la concentración de uno de
los reactivos es muy grande en comparación a la concentración del otro. En tal
caso, la concentración del reactivo en exceso puede considerarse constante con
el tiempo, por lo que la ley de velocidad quedará:
(27)
v = k' [A]
es decir, la ecuación de velocidad se transforma en una ecuación de seudoprimer orden.
Algunos ejemplos de reacciones de segundo orden son:
 Disociación del ácido iodhídrico:
2 HI --> I2 + H2
 Síntesis del ácido iodhídrico:
I2 + H2 --> 2 HI
 Hidrólisis de un éster:
RCO2 R' + NaOH --> RCO2 Na + R'OH
 Dimerización de hidrocarburos:
2 C4 H6 --> C8 H12
7.2.- La constante de equilibrio.
Equilibrio químico
Una reacción se llama reversible cuando la posibilidad de reacción es apreciable en
ambos sentidos. En este caso llega un momento en que la velocidad con que aparecen
los productos es igual a la velocidad con que éstos se recombinan para dar de nuevo los
reactivos, y en este momento se dice que se ha alcanzado el equilibrio químico.
Cuantitativamente, las concentraciones de los productos y los reactivos mantienen a
partir de este momento una relación fija si no se varían los factores que intervienen en la
reacción. Esta relación viene dada por la constante de equilibrio de la reacción, Kc
Desplazamiento del punto de equilibrio
Al variar alguno de los factores (concentración, temperatura o presión) que afectan a las
velocidades de reacción, el equilibrio se desplaza, de modo que el sistema tiende a
oponerse a la variación que afecta al equilibrio (principio de Le Chatelier). Así, si
alcanzado el equilibrio se aumenta la concentración de una de las sustancias
reaccionantes, el equilibrio se desplaza de modo que aumente la concentración de
reactivos (o a la inversa si se aumenta la concentración de un producto).
7.3.- Principio de Le Chatelier.
Principio de Le Chatelier.
Una vez que se establece el equilibrio químico en un sistema reaccionante, permanecerá
inalterado siempre que no existe algún factor externo que modifique el punto de
equilibrio. Si el sistema es sometido a factores externos, entonces por sí solo se
desplazará de tal forma que contrarreste esa tensión.
En 1888 el químico francés Henry Louis Le Chatelier establece el principio que lleva su
nombre para predecir el desplazamiento del punto de equilibrio, enunciándolo de la
siguiente manera:
"Si un sistema en equilibrio modifica sus condiciones debido a una perturbación
externa; entonces el mismo sistema se desplazará para reducir dicha alteración."
Las alteraciones son aquellas que provocan variaciones en la velocidad de reacción; por
ejemplo: concentración, presión, temperatura, etc. Estas predicciones se resumen de la
siguiente manera.
a) Concentración.
La ley de acción de masas establece que al aumentar la concentración de alguna
sustancia, el equilibrio químico se desplazará en dirección a disminuir la concentración
de la sustancia que se adicionó.
b) Temperatura.
Si se incrementa la temperatura de un sistema reaccionante, éste se desplazará en
dirección donde la reacción sea endotérmica, es decir, absorba calor. Si la temperatura
desciende, entonces el sentido del desplazamiento del equilibrio es hacia donde la
reacción sea exotérmica, es decir, libere calor.
c) Presión.
La presión es un factor externo que afecta principalmente a los sistemas en equilibrio
gaseoso, no así a los sólidos y líquidos que son virtualmente incomprensibles y no se
ven afectados de manera significativa. Por lo tanto, al aumentar la presión en un sistema
gaseoso el punto de equilibrio se desplazará hacia donde haya menor formación de
moles (menor volumen) y en caso contrario hacia donde se produzca mayor número de
moles (mayor volumen) para aliviar dicha tensión.
Los catalizadores no alteran al equilibrio químico ya que, independientemente del tipo
de catalizador que se utilice, las velocidades de reacción directa o inversa serán iguales.
7.5.- Producto de solubilidad.
También las constantes de equilibrio sirven para expresar la solubilidad de un
compuesto iónico en el agua. Estos equilibrios se representan mediante el
producto de las concentraciones molares de cada una de las especies iónicas
que se forman cuando se disuelve la substancia y se conocen como
“Constantes del Producto de Solubilidad, KPS”.
Las constantes o productos de solubilidad se encuentran tabuladas de manera
similar a las constantes de ionización de ácidos o bases débiles. Considérese,
a modo de explicación, el equilibrio de solubilidad de un compuesto como el
Yoduro de Plata. Cuando esta substancia se pone en contacto con el agua, la
parte de él que se disuelve, se disocia a iones plata e iones yoduro. La
constante de equilibrio que define la cantidad de materia que pasa a la
solución, se expresa matemáticamente como:
AgI

Ag+
+
I─
KPS
=
[Ag+] [I─]
=
10─16,08
Ahora, si llamamos “S” a la solubilidad molar del yoduro de plata, entonces es
claro que:
S2
=
10─16,08
Luego:
S
=
10─8,04 M
Y como un mol de Yoduro de plata equivale a 234,77 g., entonces,
S
=
0,0021 mg /l
Mediante el mismo mecanismo, podemos calcular la solubilidad del hidróxido
de aluminio, Al(OH)3:

Al(OH)3
(S
KPS
=
Al3+
+
3 OH─
S
+
3 S)
=
10─31,7
[Al3+] [OH─]3
Nuevamente, si llamamos “S” a la solubilidad molar del hidróxido de aluminio,
entonces:
7.6.- Solución amortiguadora.
La capacidad amortiguadora de una solución buffer es por definición, “el
número de moles de ácido o base fuerte que se requieren para modificar el pH
de un litro de esta solución en una unidad. En las valoraciones Ácido-Base, la
pendiente de la curva de valoración, (pH “vs” mls titulante), es inversamente
proporcional a la Capacidad Reguladora de la solución.
Así, en la titulación de un ácido fuerte con una base fuerte, (trazo azul de la
Figura No 10.3), el sistema tiene una considerable capacidad reguladora en los
tramos iniciales o finales de la titulación, (entre pH 1 y 2 y/o entre pH 12 y 13),
porque la pendiente de la curva en estos sectores es muy pequeña, línea casi
horizontal. Sin embargo, luego de pH aproximadamente 3 y hasta pH
aproximadamente 11, la capacidad buffer del sistema es prácticamente nula,
porque la curva se hace prácticamente vertical; en este sector, pequeñísimas
adiciones de base generan un cambio muy fuerte en el pH del sistema.