Análisis del efecto DIBL en la ganancia del amplificador intrínseco
Anuncio

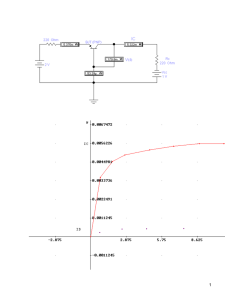
Análisis del efecto DIBL en la ganancia del amplificador intrínseco basado en el modelo Charge sheet 1. Análisis del efecto DIBL en la ganancia del amplificador intrínseco basado en el modelo Charge sheet a. I – Introducción i. 1.1 Canal corto e inversión débil ii. 1.2 ¿Qué es y a qué se debe el efecto DIBL? iii. 1.3 Modelo matemático a estudiar b. II - Modelo lineal con 1/L c. III - Modelo lineal con 1/P(L) d. IV - Análisis comparativo de resultados i. Ganancia del amplificador intrínseco e. V - Conclusiones f. VI - Nota final g. VII - Referencias I – Introducción 1.1 Canal corto e inversión débil La creciente demanda de dispositivos portátiles de larga vida útil y alto nivel de desempeño, junto a la necesidad de diseños de bajo consumo de energía (por ejemplo dispositivos médicos implantables, en el campo analógico, o microprocesadores de pequeñas dimensiones que realizan miles de millones de operaciones por segundo, en el campo digital), ha encontrado un punto de investigación en la tecnología MOS de integrados. Típicamente, diseños de baja potencia implicaban un sacrificio de velocidad y rango dinámico; por el contrario, alta velocidad y alta integración (gran cantidad de transistores) implican un incremento en la disipación de energía del circuito. Estas necesidades convergen en el diseño de circuitos integrados con transistores de pequeñas dimensiones, trabajando con bajos voltajes. La reducción de las dimensiones del transistor, implica una disminución en la longitud del canal, acercando el source y el drain entre sí. En la consideración tradicional de transistores de canal largo, se hacen diversas aproximaciones, de las cuales la más crucial es suponer que el campo eléctrico inducido sobre el canal es perpendicular al mismo, salvo en las cercanías al drain y source. Como consecuencia del acortamiento del canal, esta aproximación deja de ser aceptable, entrando en juego otros efectos llamados "efectos de canal corto". El aumento del voltaje entre Gate y Bulk (sustrato) induce una acumulación de cargas en la zona de interfase con el óxido (ver figura 1). Esta acumulación, genera una región de cargas llamada zona de inversión, dejando por debajo una región de deplexión de cargas. La figura 2 muestra la profundidad de la zona de inversión en función del voltaje Gate-Bulk; se define el Voltaje de Umbral (VT), como el voltaje VGB de transición entre las zonas de "inversión moderada" e "inversión fuerte". En los diseños tradicionales y básicos, se trabaja principalmente con los transistores en la zona llamada de inversión fuerte. La disminución de los voltajes de funcionamiento de los transistores, para reducir el consumo de dispositivos, conducen al estudio de su funcionamiento en las otras "zonas de inversión" por debajo de VT, entre las que se distinguen las zonas de inversión débil e inversión moderada, según se ve en la figura 2. También aquí se define un voltaje de transición entre ambos niveles de inversión, representado por VM. Figura 1 - (a) Transistor de canal largo; (b) canal de (a) con efectos de borde despreciados; (c) Transistor de canal corto; (d) canal de (c) con efectos de borde despreciados Figura 2 - Magnitud de la capa de inversión en función de VGB Tanto VT como VM, dependen exclusivamente de la densidad de cargas en la zona de deplexión del sustrato. En el caso de transistores de canal largo, estos voltajes dependen principalmente de VGB, siendo despreciables los efectos de aumento de la densidad de cargas en las zonas cercanas al Drain, según los modelos tradicionales del MOSFET de canal largo e inversión fuerte (se considera el caso en que VSB=0V). Como consecuencia dos grandes líneas de investigación tecnológica han convergido: el diseño de circuitos analógicos de bajo consumo, utilizando inversión débil, y el desarrollo de técnicas de fabricación de dispositivos de tamaño del orden de décimas de micras. A continuación, se estudiará el efecto inducido por el drain sobre los parámetros de funcionamiento de los MOSFET en inversión débil, utilizando un canal corto. 1.2 ¿Qué es y a qué se debe el efecto DIBL? Ambos, el voltaje de umbral (VT) y el voltaje de transición (VM) dependen de la densidad de cargas existente en la zona de deplexión del sustrato. Tradicionalmente, en los modelos de canal largo e inversión fuerte, dicha densidad de cargas se suponía dependiente exclusivamente del VGB, ya que el aumento de cargas inducido por el Drain o el Source, es despreciable. Sin embargo, el primer efecto que fue estudiado en este sentido, es el de la acumulación de cargas debido a la tensión a lo largo del canal, en particular cuando la tensión VSB>0. Éste es el llamado "efecto body". Un efecto similar es inducido por el voltaje de Drain. Al aumentar VDB, se induce un aumento en la densidad de cargas de la zona de deplexión y una diferencia en el gradiente del campo eléctrico Drain-Source. Este aumento en la densidad de cargas, para un VGB fijo, implica una nueva definición de VT y VM, en función de VGB y VDB. Un aumento en VDB induce un aumento en la densidad de cargas, implicando que, en efecto, el VGB necesario para conseguir una determinada corriente IDS en saturación, sea menor al previsto despreciando el efecto del voltaje de Drain. Cuanto menor sea VGB, y por lo tanto menor sea la densidad de cargas en el sustrato, más apreciable será el efecto de la acumulación de cargas en las zonas del Drain. Asímismo, sucede que al reducir la longitud del canal, más apreciable es el efecto del Drain sobre la densidad de cargas de deplexión. Este efecto hace que los valores de VT y VM (definidos como los valores de VGB para los cuales se tiene los límetes de las zonas de inversión fuerte, moderada y débil), disminuyan, ya que con un menor VGB se obtiene una misma (o parecida) densidad de cargas en la zona de inversión. A este efecto se le llama Disminución de Barrera Inducida por Drain o DIBL por su sigla en inglés. 1.3 Modelo matemático a estudiar El presente trabajo estudia la influencia del efecto DIBL sobre la ganancia del amplificador intrínseco en inversión débil, dada por la ecuación (1). Para este análisis se supondrá que VSB=0. Es fácil comprobar (ver Anexo I) que , entonces este parámetro es dependiente del efecto DIBL en n. Se estudiará, por lo tanto, la infuencia de dicho efecto sobre el producto VAgm/IDS. Se desprecia los efectos de modulación de largo de canal (CLM); se supondrá que no ocurre ninguna saturación de velocidad\1\ y que la ecuación (2) describe el comportamiento de la corriente drain-source (modelo Charge sheet). (1) (2) Siendo VM el voltaje que, aplicado a VGS, define la transición entre inversión débil y moderada. Esta tensión responde a la siguiente expresión: . Donde γ es el parámetro de efecto body. Es apreciable la similitud entre la expresión de VM y la de VT. La literatura modela el efecto DIBL como una variación del parámetro γ inducida por la acumulación de cargas en la zona del drain. Se tiene por lo tanto: , siendo VM el valor para canal largo del voltaje de transición. En \1\ se elabora un modelo para inversión fuerte de la variación de VT con VDS, tomando como supuesto que ΔVT es lineal con 1/L. En este trabajo se supondrá que las variaciones de VM son cualitativamente iguales a las variaciones de VT. Por esto y dado que ambas tensiones tienen una expresión aritmética similar, se deduce que el modelo encontrado para ΔVT es aplicable para ΔVM, según describe la ecuación (3). (3) En el Anexo I se realiza la deducción del valor del voltaje de Early en función del efecto DIBL. Llegando a la siguiente relación: (4) La figura 3, muestra los valores numéricos de 1/VA en función de gm/IDS del transistor M4 \2\. Cualitativamente, todos los transistores tienen una curva similar, con variaciones numéricas en 1/VA. Como nota importante para el trabajo, se destaca que se trabajó con valores de gm/IDS en un entorno de 28 V-¹. Figura 3 - 1/VA en función de gm/IDS El estudio analiza el voltaje de Early de cada transistor en inversión débil, estimado numéricamente con las medidas\2\, en relación con el modelo teórico de la ecuación (4). La misma muestra la dependencia de VA con L, y los parámetros DIBL. Sin embargo, cálculos numéricos en el siguiente apartado, basados en las medidas de \2\, muestran un severo apartamiento de los valores esperados por la ecuación anterior. Esto llevó a pensar que un primer error posible fuera suponer linealidad con 1/L; por lo tanto se buscó una linealidad con 1/P(L), siendo P(L) un polinomio de algún grado k>1. Dado que se disponía únicamente de cinco conjuntos de medidas de distintos transistores, el grado máximo que se pudo buscar fue k=4. II - Modelo lineal con 1/L La ecuación (4) es el modelo lineal. Se busca, entonces, dimensionar el producto ß1ß2. Para esto, se calcula gm/ID y VA a partir de las medidas y, luego, se despeja el producto ß1ß2. Cálculo de gm/ID Como entonces, se calcula gm/ID con la siguiente ecuación (5) Las medidas, de cada transistor, fueron realizadas a VGS variando desde 0,3V hasta 3,3V, con pasos de 0,5V. Con los valores obtenidos, se comprueba que, por cada transistor, se tiene solamente un valor de VGS que deja al FET en inversión débil; el mismo es 0,3V. Cálculo de VA Suponiendo el modelo en saturación de IDS, se pude calcular VA de acuerdo con la ecuación (6) (ver Anexo I). (6) En primera instancia, se buscó calcular VA numéricamente utilizando esta ecuación. Sin embargo, sus grandes variaciones numéricas al variar VDS, llevaron a buscar otra alternativa de cálculo. Se aproximó, entonces, la zona de saturación IDS, como una recta descripta por . Por lo que: (7) En consecuencia, se busca la recta que mejor aproxime a la zona de saturación; siendo la distancia de su intersección con el eje de las x a un VDS apropiado, el VA buscado. Como para las medidas de IDS en función de VGS, usadas para calcular gm/ID, fueron realizadas con VDS=VGS, siendo VGS=0,3V el valor para inversión débil, se tomó VDS=0,3V. De esta forma se obtuvo un valor empírico de VA. Cabe destacar que la zona, donde es aplicable la aproximación de primer grado, es acotada ya que para valores muy altos de VDS, otros efectos actúan sobre IDS. Resultados En la Tabla 1 se muestran los valores obtenidos de ß1ß2. Transistor\2\ L ß1ß2 M4 0,3 0,0466 M8 1,0 0,0385 M16 1,8 0,0545 M10 3,0 0,52215 M11 5,0 0,11785 Valor teórico --- 0,25 Tabla 1 - Valores de ß1ß2 en función de L Dada la diferencia entre los valires obtenidos y los esperados teóricamente, se prosiguió a modelar ΔVM lineal con 1/P(L). III - Modelo lineal con 1/P(L) Para este análisis se toman los valores de VA y gm/ID calculados en el punto anterior. El modelo se analiza tomando ß1=1 y ß2=0,25. Por lo tanto, se obtiene la ecuación (8) que muestra la linealidad entre P(L) y la ganancia del amplificador intrínseco: (8) Resultados Para cada transistor de largo de canal distinto, se tiene un valor empírico de P(L). La tabla 2 muestra el conjunto de valores en función de L. Transistor\2\ L P(L) M4 0,3 0,0466 M8 1,0 0,0385 M16 1,8 0,0545 M10 3,0 0,52215 M11 5,0 0,11785 Tabla 2 - Valores de P(L) en función de L Se hizo la aproximación con polinomios de primer a cuarto grado obteniéndose los resultados observados en la figura 4 y la tabla 3. Figura 4 - Gráficos de P(L) en función de L para grados 1 a 4 Grado P(L) 1 P(L) = 1.1782.L + 3.0650 2 P(L) = 0.2617.L² - 0.2322.L + 4.1898 3 P(L) = 1.2936.L³ - 9.8331.L² + 19.6910.L - 3.7523 4 P(L) = 0.4405.L^4 - 2.9694.L³ + 2.9527.L² + 6.6420.L - 0.5723 Tabla 3 - Polinomios aproximantes a los valores empíricos El test estadístico t-student de las distancias de los puntos al polinomio de primer grado, permite descartar el valor del transistor M10 con un nivel de confianza del 67,5%. Al realizar las nuevas aproximaciones con polinomios de primer a tercer grado, se obtuvieron los resultados de la tabla 4 y la figura 5, observándose resultados similares confirmando el test estadístico. Figura 5 - Gráficos de P(L) en función de L para grados 1 a 3 Grado P(L) 1 P(L) = 1.5676.L + 3.5673 2 P(L) = -0.8383.L² + 6.2669.L + 0.1982 3 P(L) = 0.5988.L³ - 5.0384.L² + 12.6948.L - 1.7617 Tabla 4 - Polinomios aproximantes a los valores empíricos IV - Análisis comparativo de resultados La figura 6 muestra los valores estimados de la ganancia del amplificador intrínseco en función de L, para el modelo propuesto en \1\, los modelos polinómicos, según la ecuación (9) y los valores empíricos. Figura 6 - Gráficos de G(V/V) en función de L (9) Ganancia del amplificador intrínseco El uso de distintos modelos del efecto DIBL influye sobre el valor de G (ganancia del amplificador intrínseco). La tabla 5 muestra los distintos valores de G, para cada longitud de canal y para cada modelo en dB (evidentemente los valores para el polinomio de tercer grado coinciden con los empíricos). L Empírico Teórico Grado 1 Grado 2 Grado 3 0.3 16.7 2.1 24.7 18.6 16.7 1.0 28.8 11.6 26.5 26.8 28.8 1.8 30.9 17.1 28.4 31.1 30.9 5.0 33.1 26.3 33.6 33.2 33.1 Tabla 5 - Ganancias en dB para cada L en cada modelo V - Conclusiones Se presentó un desarrollo teórico del valor de la ganancia del amplificador intrínseco, basado en el modelo Charge sheet y suponiendo una dependencia lineal con 1/L. Luego, dado que se apreció una gran discrepancia entre los valores teóricos y empíricos, se buscó un modelo polinómico en L. El estudio comparativo entre los distintos modelos, no muestran una gran diferencia en dB si bien, en valores absolutos, se tienen ganancias hasta 1,5 veces mayores. Como el efecto DIBL es uno de los efectos conocidos como de canal corto, es factible suponer que para L muy grande, el VA también tenderá a ser muy grande, por lo que se deduce que el modelo polinómico más adecuado debe ser de grado impar; en el caso del presente trabajo, se concluye usar el modelo polinómico de tercer grado: (11) Sin embargo, es correcto suponer que a medida que aumenta L, las variaciones sobre la ganancia, tendrán un cambio relativo menor. Es por esto que se propone realizar, a posteriori y con mayor cantidad de puntos en L, un estudio de dependencia logarítmica o exponencial. Se propone, asimismo, completar el presente trabajo repitiendo las medidas para otros valores de VGS en inversión débil. VI - Nota final El efecto de DIBL sobre el canal es notoriamente apreciable por encima de otros efectos como CLM, estando el canal en la zona de inversión débil. Esto implicó un inconveniente a la hora de los análisis ya que del conjunto de medidas que se tienen para distintos transistores, solamente una medida por transistor corresponde a esta zona. Debido a esto, el estudio supone que el valor medido en esta zona es preciso y exacto. VII - Referencias 1. "Operation and modelling of the MOS transistor" - Tsividis Y. McGraw--Hill, 1987 2. Medidas de Alessandro Girardi; Universidade Federal do Rio Grande do Sul 3. M.C. Smith, M.L. Simpson, M.J. Paulus, J.M. Rochelle, D.H. Lowndes, C.E. Thomas, J.A. Moore, L.R. Baylor, D.B. Geohegan, G.E. Jellison, V.I. Merkulov, A.A. Puretzky, E. Voelkl, J.M. Vann, "Modeling and Simulation of Short- Channel MOSFETs Operating in Deep Weak Inversion," mwscas, p. 24, 1998 Midwest Symposium on Systems and Circuits, 1998.