02-06-07 A.pdf

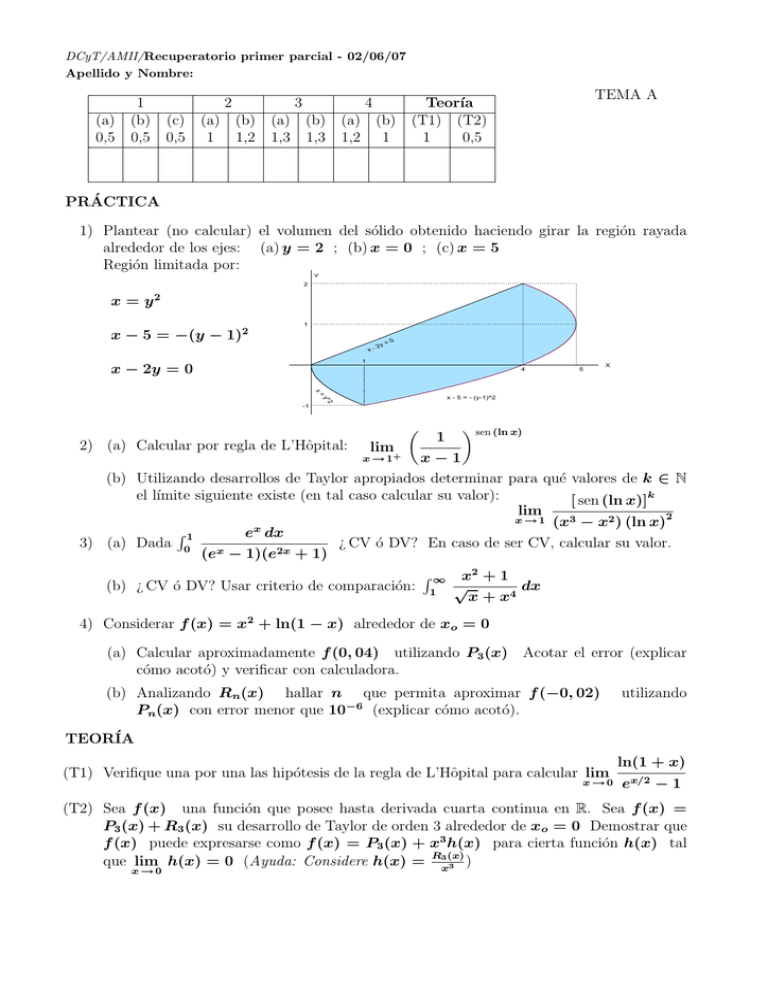
DCyT/AMII/Recuperatorio primer parcial - 02/06/07
Apellido y Nombre:
1
(a) (b)
0,5 0,5
2
3
TEMA A
4
Teorı́a
(c) (a) (b) (a) (b) (a) (b) (T1) (T2)
0,5 1 1,2 1,3 1,3 1,2 1
1
0,5
PRÁCTICA
1) Plantear (no calcular) el volumen del sólido obtenido haciendo girar la región rayada
alrededor de los ejes: (a) y = 2 ; (b) x = 0 ; (c) x = 5
Región limitada por:
Y
2
x = y2
x − 5 = −(y − 1)2
1
x-
2y
=0
1
x − 2y = 0
4
5
X
x
=
2
y^
x - 5 = - (y-1)^2
-1
2) (a) Calcular por regla de L’Hôpital:
lim
µ
1
¶ sen (ln x)
x−1
(b) Utilizando desarrollos de Taylor apropiados determinar para qué valores de k ∈ N
el lı́mite siguiente existe (en tal caso calcular su valor):
[ sen (ln x)]k
lim
x → 1 (x3 − x2 ) (ln x)2
x
R1
e dx
¿ CV ó DV? En caso de ser CV, calcular su valor.
3) (a) Dada 0
(ex − 1)(e2x + 1)
R ∞ x2 + 1
(b) ¿ CV ó DV? Usar criterio de comparación: 1 √
dx
x + x4
x → 1+
4) Considerar f (x) = x2 + ln(1 − x) alrededor de xo = 0
(a) Calcular aproximadamente f (0, 04) utilizando P3 (x) Acotar el error (explicar
cómo acotó) y verificar con calculadora.
(b) Analizando Rn (x) hallar n que permita aproximar f (−0, 02)
Pn (x) con error menor que 10−6 (explicar cómo acotó).
utilizando
TEORÍA
(T1) Verifique una por una las hipótesis de la regla de L’Hôpital para calcular lim
x→0
ln(1 + x)
ex/2 − 1
(T2) Sea f (x) una función que posee hasta derivada cuarta continua en R. Sea f (x) =
P3 (x) + R3 (x) su desarrollo de Taylor de orden 3 alrededor de xo = 0 Demostrar que
f (x) puede expresarse como f (x) = P3 (x) + x3 h(x) para cierta función h(x) tal
)
que lim h(x) = 0 (Ayuda: Considere h(x) = R3x(x)
3
x→0