Diseño y evaluación de Torre de Enfriamiento Autoventiladas (TEA)

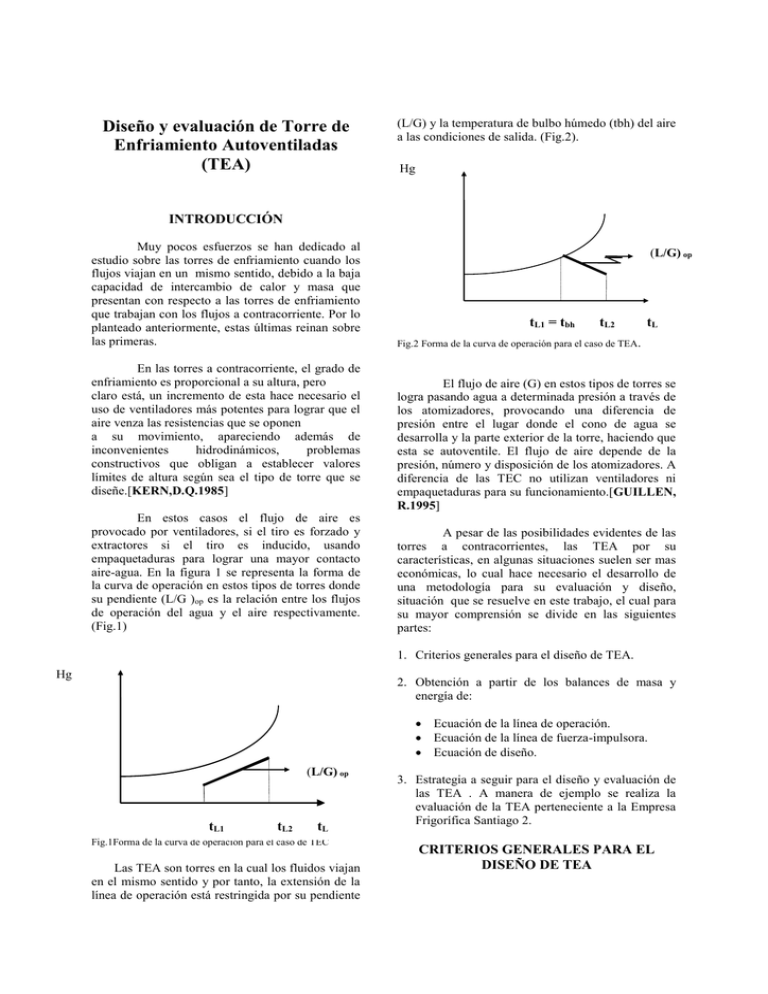
Diseño y evaluación de Torre de
Enfriamiento Autoventiladas
(TEA)
(L/G) y la temperatura de bulbo húmedo (tbh) del aire
a las condiciones de salida. (Fig.2).
Hg
INTRODUCCIÓN
Muy pocos esfuerzos se han dedicado al
estudio sobre las torres de enfriamiento cuando los
flujos viajan en un mismo sentido, debido a la baja
capacidad de intercambio de calor y masa que
presentan con respecto a las torres de enfriamiento
que trabajan con los flujos a contracorriente. Por lo
planteado anteriormente, estas últimas reinan sobre
las primeras.
En las torres a contracorriente, el grado de
enfriamiento es proporcional a su altura, pero
claro está, un incremento de esta hace necesario el
uso de ventiladores más potentes para lograr que el
aire venza las resistencias que se oponen
a su movimiento, apareciendo además de
inconvenientes
hidrodinámicos,
problemas
constructivos que obligan a establecer valores
límites de altura según sea el tipo de torre que se
diseñe.[KERN,D.Q.1985]
En estos casos el flujo de aire es
provocado por ventiladores, si el tiro es forzado y
extractores si el tiro es inducido, usando
empaquetaduras para lograr una mayor contacto
aire-agua. En la figura 1 se representa la forma de
la curva de operación en estos tipos de torres donde
su pendiente (L/G )op es la relación entre los flujos
de operación del agua y el aire respectivamente.
(Fig.1)
(L/G) op
tL1 = tbh
tL2
tL
Fig.2 Forma de la curva de operación para el caso de TEA.
El flujo de aire (G) en estos tipos de torres se
logra pasando agua a determinada presión a través de
los atomizadores, provocando una diferencia de
presión entre el lugar donde el cono de agua se
desarrolla y la parte exterior de la torre, haciendo que
esta se autoventile. El flujo de aire depende de la
presión, número y disposición de los atomizadores. A
diferencia de las TEC no utilizan ventiladores ni
empaquetaduras para su funcionamiento.[GUILLEN,
R.1995]
A pesar de las posibilidades evidentes de las
torres a contracorrientes, las TEA por su
características, en algunas situaciones suelen ser mas
económicas, lo cual hace necesario el desarrollo de
una metodología para su evaluación y diseño,
situación que se resuelve en este trabajo, el cual para
su mayor comprensión se divide en las siguientes
partes:
1. Criterios generales para el diseño de TEA.
Hg
2. Obtención a partir de los balances de masa y
energía de:
 Ecuación de la línea de operación.
 Ecuación de la línea de fuerza-impulsora.
 Ecuación de diseño.
(L/G) op
tL1
tL2
tL
Fig.1Forma de la curva de operación para el caso de TEC
Las TEA son torres en la cual los fluidos viajan
en el mismo sentido y por tanto, la extensión de la
línea de operación está restringida por su pendiente
3. Estrategia a seguir para el diseño y evaluación de
las TEA . A manera de ejemplo se realiza la
evaluación de la TEA perteneciente a la Empresa
Frigorífica Santiago 2.
CRITERIOS GENERALES PARA EL
DISEÑO DE TEA
Resulta antieconómico diseñar torres
basándose en la temperatura de bulbo húmedo del
aire que interacciona con la corriente de agua a la
salida o sea para el caso de TEC corresponde con la
tbh del aire entrante y para las TEA con la tbh de la
corriente de aire saliente, debiendo llegarse a un
compromiso entre las condiciones máximas y
medias.
Uno de los métodos sugeridos es el uso de
la llamada temperatura húmeda de "5 por 100", que
se define como la temperatura húmeda que no es
sobrepasada por más del 5 % del número total de
horas durante los meses de Junio a Septiembre, y
que se calcula del estudio de los datos
meteorológicos locales. [BADGER,W.L.1967]
El procedimiento de diseño consiste en un
número de etapas que son:
a) Selección de la aproximación de
temperatura
La aproximación de la temperatura se
define como la diferencia entre la temperatura del
agua de salida y la temperatura de bulbo húmedo
del aire de entrada es decir, la aproximación de la
temperatura del agua de salida a su valor mínimo
posible.
Debe observarse que el agua en estos casos
no puede enfriarse por debajo de la temperatura de
bulbo húmedo del aire a la salida, la cual coincide
con el punto de intersección entre la línea de
operación y la curva de equilibrio, y donde la
fuerza impulsora se anula.
Los autores proponen un método para la
selección de la aproximación de temperatura
llamado "Método del 60% de Eficacia" y consiste
en considerar que la eficiencia de enfriamiento de
las TEA es de un 60% con respecto a las máxima
diferencia de temperatura que puede alcanzarse
teóricamente (la temperatura de bulbo húmedo).
c) Evaluación de la condiciones de operación:
En el cálculo de las torres de enfriamiento las
condiciones de equilibrio y operación se expresa
en función de la Entalpía del aire y de la
temperatura del agua. La temperatura húmeda del
aire y la "aproximación de temperatura" se
especifican o se suponen y la temperatura del
agua a la entrada resulta conocida en las
condiciones del proceso. Por tanto, la única
condición de operación a determinar es la entalpía
del aire a la salida. [SAWISTOWWSKI,H.1967]
d) Cálculo de la altura de la torre
Conociendo la línea de equilibrio y de
operación, ambas dibujadas como entalpía del aire
frente a la temperatura del agua, se calcula el número
de unidades de transferencia y se multiplica por la
altura de una unidad de transferencia para obtener la
altura de la torre.
e) Cálculo de la razón optima aire-agua
Con el incremento de la presión de atomización
para el caso de las TEA, disminuye la relación (L/G)
hasta cierto valor a partir del cual el agua comienza a
elevar su temperatura de salida debido al reducido
tiempo que permanecen las gotas dentro de la torre,
provocado por las altas velocidades que desarrollan al
incrementarse el flujo de aire.
Con el incremento de la presión de
atomización se incrementa también el flujo de aire
(G), haciendo que la relación (L/G) disminuya y por
tanto se logre un mayor enfriamiento, que varia desde
cero cuando la pendiente (L/G) =  hasta el t
correspondiente a la razón (L/G) = 0. Lo anterior es
cierto solo si el tiempo de residencia de las gotas de
agua es suficiente para que se produzca el
intercambio aire - agua, a partir de cierto valor de
tiempo de residencia, la temperatura de salida del
agua comienza a incrementarse. El punto en el cual se
observa este cambio de tendencia corresponde a la
razón (L/G) de operación óptima.
Balance de masa y energía
La expresión es la siguiente:
t t
  L 2 L1
t L 2  tbh
Balance de masa en un diferencial dz de la
torre
Luego:
tL1 = tL2 -  tL2 - tbh)
b) Cálculo de la sección transversal de la
Torre:
La sección transversal de la torre dependen
de la presión, tipo, número y disposición de los
atomizadores.
Gs
tg2
Hg2
Y2
L
tL2
TM
L
dz
Gs
LC L dt L  GdH G
2
2
1
1
LC L  dt L  G S  dH G
Resolviendo la integral
LC L t L 2  t L1   GS  HG 2  HG1 
LC L HG 2  HG1

GS
t L 2  t L1
Balance de Masa
L  dL  G S Y  L  GS  Y  dY 
L  dL  G S Y  L  GS Y  G S dY
dL  G S dY
Esta ecuación define la cantidad de agua
que se evapora durante el proceso y que es
absorbida por el aire para incrementar su humedad.
Gs
tg
HG
Y
L+dL
tL+dtL
HL+dHL
dz
Para el caso de torres autoventiladas en las cuales el
flujo es paralelo
Hg2 < Hg1 , por tanto la pendiente es negativa.

LC L H g 2  H g1

GS
t L 2  t L1
(4)
Ecuación de diseño. Utilización de la
diferencia de Entalpía como fuerza
impulsora.[KASATKIN, G.1985]
LdH L  LCL dt L  q   L dst L  t i 
para un ds
TM
ds  a  s  d z
LC L dt L   L  a  s  dzt L  t i 
L
tL
HL
Gs+dG
tg +d tg
HG
+dHg
Y+dY
Balance de energía
 L  dL H L  dH L   GS HG  LH L  GS  HG  dHG 
LH L  LdH L  dLH L  dLdH L  GS HG  LH L  GS HG  GS dHG
Teniendo en cuenta que las cantidades de
agua evaporada durante el proceso puede
despreciarse si se compara con el flujo de agua de
enfriamiento y debido al alto valor de la humedad
relativa en nuestro país (superior a 90% ), se puede
plantear que dL  0.
LdH L  GS dHG
Obtención de la línea de operación
A partir de la ecuación obtenida por el Balance de
energía.
LdH L  LCL dt L
Sustituyendo ( 3 ) en ( 2 ) se obtiene que:
2
Z
LC L
dt L
 L  a  s 1 t L  t i
pero como
LH L  G S dH G
G S dH G  CG dt G G S  K G aMP Hi  H G dz
2
Z
GS
dH

KG aMP 1  Hi  HG 
(5)
Línea de fuerza impulsora
Según la ecuación  2 )
LdH L  GS dHG
LdH L  LC L dt L   L at L  t i dz
GS dHG  GS CG dt G  GS  o dY


GS CG dt G   G a t i  t g dz
GS  o dY  KG aYi  Y  o dz
Sustituyendo y efectuando
GS dHG   G ati  t G dz  KG aYi  Y  o dz
Dividiendo entre KG
G S dH G  G

t i  t G adz  Yi  Y  o adz
KG
KG

G S dH G   G

t i  t G   Y i Y  o  adz
KG
 KG

pero se conoce
G
S 
 CG  C 
KG
 Pr 
0.56
En ausencia de información sobre los
coeficientes puede suponerse en una primera
aproximación, ti es igual a tL, o lo que es lo mismo
que la fase gaseosa no ofrece resistencia a la
transferencia de masa.
para sistemas aire-agua a p1 atm
SC
1
Pr


GS dH G
 CG t i  t G   Yi  Y  o adz
KG
CG t i  Yi  o  Hi
CG t G  Y o  H G
El procedimiento anterior no da información
alguna sobre los cambios en la temperatura y
humedad de la mezcla aire-agua a lo largo de la torre.
Para los casos en que la información sea necesaria se
puede utilizar el método gráfico de Mickley
[SAWISTOWWSKI,H.1967]
GS dH G  K G aPM  Hi  H G dz
LC L dt i   L at i  t L dz
Sustituyendo en  2 )
KG aPM  Hi  HG    L at i  t L 
 La
H  HG
 i
KG aPM
ti  t L
KG aPM

Hi  H G
t L  ti
GCG dt G   G ati  t G dz
(7)
GdH  KG aPM Hi  HG dz
(8)
Dividiendo 7 entre 8
G CG dt G
Para torres autoventiladas ti < tL por lo que
la ecuación de la línea de fuerza impulsora nos
queda
 La
En este caso un punto de la línea de
operación tiene su correspondiente sobre la curva de
equilibrio situado directamente por encima de él, o
sea la pendiente es vertical.
Método de Mickley
GS dH G  K G adz Hi  H G 

Si se dispone información sobre los
coeficientes anteriores la ecuación de la línea de
fuerza impulsora se utiliza para determinar puntos
correspondientes sobre la línea de operación y sobre
la curva de equilibrio; estos puntos se emplean para
determinar la diferencia de Entalpía ( Hi - HG )
necesaria para obtener gráficamente el valor de la
integral de la ecuación ( 5 ). Esta ecuación se utiliza
para determinar la altura necesaria para alcanzar los
valores deseados de temperatura del agua a la salida
de la torre ( tL1 ).
(6)
REPRESENTACIÓN GRÁFICA
La ecuación de la línea de fuerza
impulsora ( 6 ) es la ecuación de una línea recta
que une (HG1, tL1 ), que es un punto de la línea de
operación, con el punto ( Hi, ti ), situado sobre la
curva de equilibrio. Su pendiente es el primer
miembro de la ecuación ( 6 ), es el cociente del
coeficiente de transferencia de calor en la fase
liquida y el coeficiente de transferencia de masa en
fase
gaseosa
multiplicado
por
ciertas
constantes.[TREYBAL,R.E.1986]
GdH

 G at i  t G dz
KG aPM  Hi  H G dz
  H  HG  
dH KG aPM

CG  i

dt G
 Ga
 t i  t G  
 Ga
 CG
KG aPM
dH Hi  H G

dt G
ti  t G
(9)
EJEMPLO DE EVALUACIÓN DE UNA
TORRE AUTOVENTILADA
Con el objetivo de detallar la metodología de
evaluación dada en el trabajo se tomo una torre
autoventilada perteneciente a la empresa frigorífica
Santiago 2, la cual es la encargada del enfriamiento
del agua proveniente de los condensadores de
amoniaco del sistema.
La torre tiene la siguientes
constructiva:
1. Sección transversal: 46.89 m²
2. Altura : 5 m
3. Número de atomizadores: 260
características
Para el calculo de la integral se aplicara el
método de los trapecios, el cual se ordena en la
siguiente tabla:
Las mediciones realizadas en esta
instalación arrojaron los siguientes resultados
promedios: [ARGUELLES,J.A.1987]
1. Temperatura de entrada del agua ( tL2 ): 30.1°C
2. Temperatura de salida del agua ( tL1 ): 28°C
3. Temperatura de bulbo húmedo del aire a la
entrada ( tbh ): 23.8°C
4. Temperatura de bulbo seco del aire a la entrada
( tG2 ):29.2°C
5. Temperatura del aire a la salida ( tG1 ): 26.5°C
6. Flujo de agua de enfriamiento ( L ): 156 kg / s
7. Flujo del aire a la entrada ( G ): 206.69 kg / s
Los cálculos se realizaran siguiendo los
pasos del algoritmo de calculo propuesto, para la
evaluación de torre de enfriamiento autoventilada,
en este trabajo.
1) Ubicación de la línea de operación:
Punto 1
Punto 2
Hg1 = 22,9
Hg2 = 21,4
tL1 = 28 ºC
tL2 = 30,1 ºC
1
Hi  HG
HG
Hi
21.40
21.65
21.90
22.15
22.40
22.65
22.90
22.75
22.90
23.05
23.20
23.35
23.50
23.65
HG 1

HG 2
0.74
0.80
0.869
0.95
1.05
1.176
1.33
R
0.43
0.80
0.869
0.95
1.05
1.176
0.665
dH
  R  H  5,940.25  1485
.
H i  HG
Kga  0.045
=
kmol
kmol
 162 3
m 3  s  atm
m  h  atm
Luego, es posible calcula el coeficiente de
transferencia de calor en la fase líquida.
kmol
kmol
 L a  0.01305 3
 46,98 3
m  s  atm
m  h  atm
CS E  0.24  0.45 * Y2
CS E  0.24  0.45 * 0.01305
2) Determinación de los coeficientes de
transferencia de calor y transferencia de masa, a
partir de datos experimentales.
Al tener definidos los puntos de entrada y
salida del aire se supone un valor cualquiera de
pendiente de la linea de fuerza impulsora, por
ejemplo:

 La
KG a
CS E  0.2459
CS S  0.24  0.45 * Y1
CS S  0.24  0.45 * 0.0235
CS S  0.2505
CS 
 0,29
Al realizar el procedimiento con esta
pendiente de la línea de fuerza impulsora
obtenemos un valor de tG1 = 26.4°C, que
prácticamente
es
igual
al
medido
experimentalmente, por lo que aceptamos la línea
como verdadera. Luego es posible calcular el
coeficiente de transferencia de masa en la fase
gaseosa a partir de la ecuación de diseño.
CS E  CS S
2
CS  0.25
 G a  CS * KG a
 G a  0.25 * 162
 G a  40.5

 La
KG a
 0,29
Determinación de la variación máxima de
temperatura teórica.
H
KG a 
206.69 G 1 dH
1295 HG 2 Hi  H G
Para nuestro cas, la temperatura de bulbo
húmedo es tL1max  26.5C.
Luego tmax = 30-26.5
tmax = 3.5C
?Cual será la altura necesaria para lograr el
máximo enfriamiento?. Para contestar a esta
pregunta se hace necesario considerar que la línea
de operación toca la curva de equilibrio.
Aplicando el método de los trapecios se
obtiene
HG
Hi
1
Hi  HG
RT
tL1 ( C 
Z(m
21.40
21.65
21.90
22.15
22.40
22.65
22.90
23.15
23.40
23.65
23.90
24.15
22.75
22.90
23.05
23.20
23.35
23.50
23.65
23.80
23.95
24.01
24.05
24.15
0.74
0.80
0.869
0.95
1.05
1.176
1.33
1.538
1.818
2.86
6.67

0.43
0.80
0.869
0.95
1.05
1.176
1.33
1.538
1.818
2.86
6.67

30.00
29.68
29.36
29.05
28.73
28.41
28.09
27.77
27.46
27.13
26.82
26.50
0.00
0.70
1.40
2.17
3.02
3.96
5.00
6.23
7.64
9.62
13.64

ANÁLISIS DE LOS RESULTADOS
Las TEA presentan características particulares que
las diferencian con respecto a las torres de
enfriamiento a contracorrientes (TEA), los criterios
generales para su diseño constituyen una guía para
lograr comprender el porque el uso de las TEA está
limitado a determinados procesos y sus máximas
posibilidades de enfriamiento coinciden con la
diferencia entre la temperatura de entrada del agua
(tL2) y la de bulbo húmedo del aire a la salida
(tbh1), estas diferencias serán más amplias en la
medida en que el aire entre menos húmedo.
La línea de operación en las TEA es una línea de
fuerza impulsora que se anula cuando toca la curva
de equilibrio. Este punto coincide con la menor
temperatura que puede alcanzar el agua
teóricamente. La eficacia de estas torres depende
del grado de acercamiento entre la verdadera
temperatura del agua a la salida y la obtenida
teóricamente. La velocidad de transferencia de
masa decrece a lo largo de la torre hasta que llega
un momento en que se anula, el decrecimiento de
esta velocidad es proporcional a la disminución de
la diferencia (tL1 - tbh1).
Cuando la transferencia de masa cesa (tL1 = thb),
para lograr mayor enfriamiento es necesario la
utilización de TEA en serie o sea bombear
nuevamente el agua a una segunda torre. Lo
anterior es válido hasta cierto valor de diferencia de
temperatura (tL2 - tbh2), la cual es cero teóricamente
y en la práctica se calcula a través de la expresión
dada por los autores para la aproximación límite. Para
el caso anterior es necesario tener en cuenta criterios
económicos y estudio de factibilidad.
Para el diseño de TEA, es necesario un valor medio
del coeficiente volumétrico de transferencia de masa
(Kga), el cual puede estimarse a partir de la
evaluación de TEA.
La evaluación de la TEA del Frigorífico Santiago 2,
recomienda realizar un estudio sobre la posibilidad de
instalar TEA en serie ya que para enfriar 1ºC más se
necesitan 5 m adicionales o sea 10 m de altura en
total. Lo anterior hace que en la práctica la
temperatura de salida del agua (tL1) sea mayor que la
temperatura de bulbo húmedo del aire a la salida
(tbh1), sugiriendo tomar una eficiencia del 60 % para
calcular de esta manera (tL1).
El grado de enfriamiento a lograr en estas torres
depende de la relación (L/G), la entalpía de entrada y
salida del aire y la temperatura del agua. La relación
(L/G) depende del diseño mecánico de los spray. El
máximo enfriamiento en las TEA no se establece por
voluntad del hombre ya que este está dominado por
leyes físicas que impone la naturaleza.
CONCLUSIONES
1. El carácter lineal de la línea de operación esta
dado bajo la condición de que las cantidades de
agua evaporada en el proceso es despreciable con
respecto al flujo total de agua que circula por la
torre.
2. La conclusión anterior se reafirma para lugares
donde la humedad relativa del aire es elevada,
como es el caso de nuestro país.
S - Sección transversal de la torre. m2
3. La fuerza impulsora del proceso de
transferencia de calor y masa disminuye a
medida que se avanza a lo largo de la torre o sea
en el sentido en el que viajan los flujos.
ti - Temperatura de la interface agua-aire. ºC
tG - Temperatura del aire. ºC
tL - Temperatura del agua. ºC
Y - Humedad absoluta. kg agua / kg mezcla
4. Según la relación entre el flujo de agua y el
flujo de aire (L/G) que participa en el proceso y
la temperatura de entrada del agua, así será el
grado de enfriamiento que puede lograrse.
5. Para incrementar el grado de enfriamiento será
necesario el uso de TEA en serie.
Z - Altura de la torre. m
G - Coeficiente de transferencia de calor en la fase
gaseosa. Kcal / h.m2 ºC
L - Coeficiente de transferencia de calor en la fase
líquida. Kcal / h.m2 ºC
RECOMENDACIONES
o - Calor latente de vaporización. Kcal / kg
1. Realizar en las torres instaladas mediciones,
para a partir de estos datos experimentales
obtener ecuaciones empíricas que describan el
comportamiento de los coeficientes de
transferencia de masa en función de las
variables que lo afectan.
2. Optimizar los factores que afectan el proceso de
humidificación.
3. Determinar a partir de cálculos económicos la
factibilidad de aplicación de las torres de
enfriamiento autoventiladas con respecto a las
torres a contracorriente o viceversa.
4. Realizar un análisis del comportamiento de la
relación entre el flujo de agua y el flujo de aire
(L/G) ante la variación de la disposición de los
atomizadores en el diseño mecánico.
NOMENCLATURA
a - Area de la superficie interfacial por unidad de
volumen (m2 / m3).
PALABRAS CLAVES
Torres de enfriamiento, refrigeración, humidificación.
BIBLIOGRAFÍA
[1] KERN, D. Q. Procesos de Transferencia de
Calor. Edición Revolucionaria. La Habana, 1969.
[2] GUILLEN, R. Estudio Termotécnico de Torres
de Enfriamiento Autoventiladas Tesis de
Maestrado. Universidad de Oriente. Cuba. 1995
[3] BADGER, W. L. Introducción a la Ingeniería
Química. Ediciones del Castillo. Santo Domingo,
1967.
[4] SAWISTOWWSKI, H. Método de Cálculo en
los Procesos de Transferencia de Masa. Editorial
Alhambra. Madrid, 1967.
CG , CL - Capacidad calorífica del aire y el agua
respectivamente. Kcal / kg aire seco ºC.
[5] KASATKIN, A. G. Operaciones Básicas y
Aparatos en la Tecnología Química Tomo II.
Editorial Pueblo y Educación, La Habana, 1985.
CsE , CSS - Calor húmedo del aire a la entrada y
salida de la torre respectivamente.
Kcal / h.m2 ºC
[6] TREYBAL, R. E. Operaciones con
Transferencia de Masa. Edición Revolucionaria. La
Habana, 1986.
GS - Velocidad másica del aire. kg aire seco /h.m2.
[7] BIRD, R. B. Fenómenos de Transporte.
Editorial Reverté. Barcelona. 1975.
H - Entalpía. Kcal / kg aire seco.
KG - Coeficiente de transferencia de masa en la fase
gaseosa. kmol / h.m2 atm.
M - Peso molecular del aire. kg / kmol.
P - Presión total. atm
[8] ARGUELLES, J. A. Mediciones de Eventos
Dinámicos y Mecánicos. Editorial Pueblo y
Educación. La Habana, 1987.
[9] PERRY, R. Chemical Ingenees HandBook.
Editorial Revolucionaria, 1979.