determinacion del calor específico

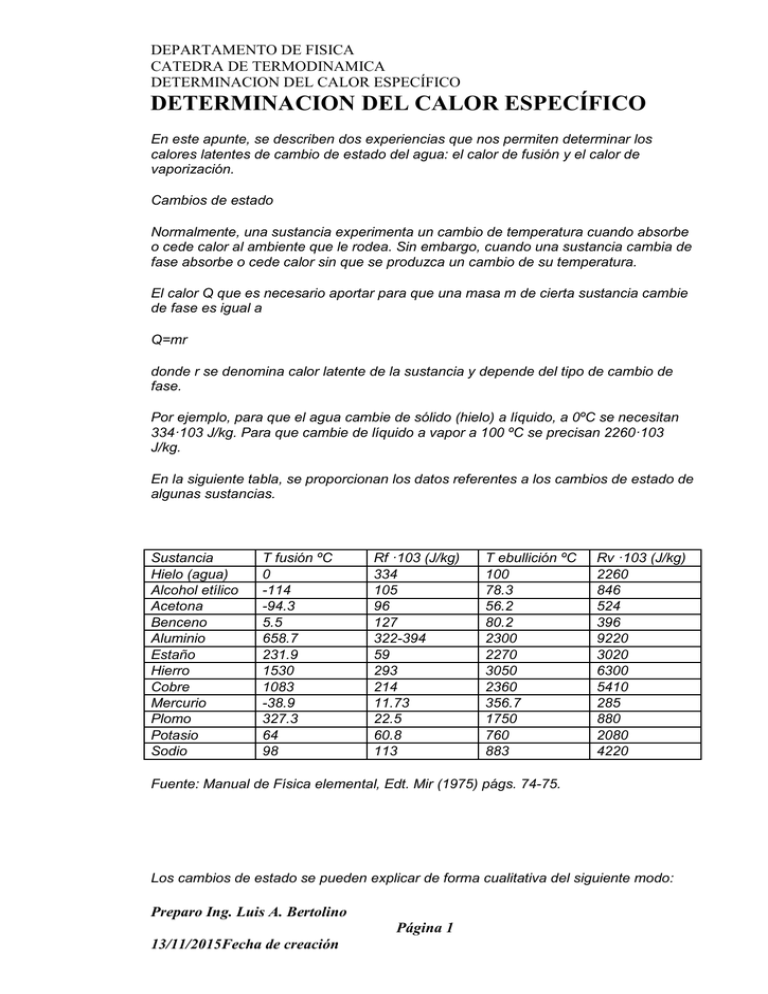
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
DETERMINACION DEL CALOR ESPECÍFICO
En este apunte, se describen dos experiencias que nos permiten determinar los
calores latentes de cambio de estado del agua: el calor de fusión y el calor de
vaporización.
Cambios de estado
Normalmente, una sustancia experimenta un cambio de temperatura cuando absorbe
o cede calor al ambiente que le rodea. Sin embargo, cuando una sustancia cambia de
fase absorbe o cede calor sin que se produzca un cambio de su temperatura.
El calor Q que es necesario aportar para que una masa m de cierta sustancia cambie
de fase es igual a
Q=mr
donde r se denomina calor latente de la sustancia y depende del tipo de cambio de
fase.
Por ejemplo, para que el agua cambie de sólido (hielo) a líquido, a 0ºC se necesitan
334·103 J/kg. Para que cambie de líquido a vapor a 100 ºC se precisan 2260·103
J/kg.
En la siguiente tabla, se proporcionan los datos referentes a los cambios de estado de
algunas sustancias.
Sustancia
Hielo (agua)
Alcohol etílico
Acetona
Benceno
Aluminio
Estaño
Hierro
Cobre
Mercurio
Plomo
Potasio
Sodio
T fusión ºC
0
-114
-94.3
5.5
658.7
231.9
1530
1083
-38.9
327.3
64
98
Rf ·103 (J/kg)
334
105
96
127
322-394
59
293
214
11.73
22.5
60.8
113
T ebullición ºC
100
78.3
56.2
80.2
2300
2270
3050
2360
356.7
1750
760
883
Rv ·103 (J/kg)
2260
846
524
396
9220
3020
6300
5410
285
880
2080
4220
Fuente: Manual de Física elemental, Edt. Mir (1975) págs. 74-75.
Los cambios de estado se pueden explicar de forma cualitativa del siguiente modo:
Preparo Ing. Luis A. Bertolino
Página 1
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
En un sólido los átomos y moléculas ocupan las posiciones fijas de los nudos de una
red cristalina. Un sólido tiene en ausencia de fuerzas externas un volumen fijo y una
forma determinada.
Los átomos y moléculas vibran, alrededor de sus posiciones de equilibrio estable,
cada vez con mayor amplitud a medida que se incrementa la temperatura. Llega un
momento en el que vencen a las fuerzas de atracción que mantienen a los átomos en
sus posiciones fijas y el sólido se convierte en líquido.
Los átomos y moléculas siguen unidos por las fuerzas de atracción, pero pueden
moverse unos respecto de los otros, lo que hace que los líquidos se adapten al
recipiente que los contiene pero mantengan un volumen constante.
Cuando se incrementa aún más la temperatura, se vencen las fuerzas de atracción
que mantienen unidos a los átomos y moléculas en el líquido.
Las moléculas están alejadas unas de las otras, se pueden mover por todo el
recipiente que las contiene y solamente interaccionan cuando están muy próximas
entre sí, en el momento en el que chocan. Un gas adopta la forma del recipiente que
lo contiene y tiende a ocupar todo el volumen disponible.
Un ejemplo clásico en el que se usan los conceptos de calor específico y calor latente
es el siguiente:
Ejemplo :
Determinar el calor que hay que suministrar para convertir 1g de hielo a -20 ºC en
vapor a 100ºC. Los datos son los siguientes:
Calor específico del hielo ch=2090 J/(kg K) Aprox.: ½ del Agua.
Calor de fusión del hielo Rf=334·103 J/kg
Calor específico del agua c=4180 J/(kg K)
Calor de vaporización del agua Rv=2260·103 J/kg
Etapas:
Se eleva la temperatura de 1g de hielo de -20ºC a 0ºC
Q1=0.001·2090·(0-(-20))=41.8 J
Se funde el hielo
Q2=0.001·334·103=334 J
Se eleva la temperatura del agua de 0º C a 100 ºC
Q3=0.001·4180·(100-0)=418 J
Preparo Ing. Luis A. Bertolino
Página 2
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Se convierte 1 g de agua a 100ºC en vapor a la misma temperatura
Q4=0.001·2260·103=2260 J
El calor total Q=Q1+Q2+Q3+Q4=3053.8 J.
En la figura, se muestra cómo se va incrementando la temperatura a medida que se
aporta calor al sistema. La vaporización del agua requiere de gran cantidad de calor
como podemos observar en la gráfica (no está hecha a escala) y en los cálculos
realizados en el ejemplo.
Si disponemos de una fuente de calor que suministra una energía a razón constante
de q J/s podemos calcular la duración de cada una de las etapas
Medida del calor de fusión
Para determinar el calor de fusión del hielo se pueden seguir dos procedimientos:
Se mide la energía (potencia por tiempo) suministrada por un calentador eléctrico a
una masa m de hielo a 0º C que se convierte en agua a la misma temperatura.
Se introduce una masa m de hielo a un calorímetro con agua a una temperatura T
ligeramente por encima de la temperatura ambiente Ta y se agita la mezcla hasta que
el hielo se funde completamente. Se elige la masa m del hielo de modo que la
temperatura Te de equilibrio esté ligeramente por debajo de la temperatura ambiente,
es decir, de modo que T-Ta≈T-Te.
De este modo, el calor cedido al ambiente en la primera etapa de la experiencia se
compensa con el calor ganado en la segunda etapa.
En la experiencia que se describe a continuación, se emplea el procedimiento de las
mezclas pero no se tiene en cuenta las pérdidas o ganancias de calor entre el
calorímetro y el medio ambiente.
Preparo Ing. Luis A. Bertolino
Página 3
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Una masa ma de agua a la temperatura inicial Ta se mezcla con una masa mh de
hielo a 0º C en un calorímetro. La mezcla de agua y hielo se agita hasta que se
alcanza una temperatura final de equilibrio Te.
Pueden ocurrir dos casos
Se funde una parte m de la masa inicial mh de hielo, quedando una mezcla formada
por hielo (mh-m) y agua (ma+m) a la temperatura final de Te=0ºC.
El calor absorbido por el hielo es Q1=m·Lf
El calor cedido por el agua es Q2=ma·c·(0-Ta)
Si el calorímetro está perfectamente aislado, no pierde ni gana calor, se cumplirá que
Q1+ Q2=0
(1)
Si se funde todo el hielo, el estado final es una masa (mh+ma) de agua a la
temperatura final Te>0.
Preparo Ing. Luis A. Bertolino
Página 4
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Ahora tenemos que tener en cuenta que la masa mh de hielo se convierte en agua y a
continuación eleva su temperatura de 0ºC a Te. Por otra parte, el calorímetro (su
masa equivalente en agua k) eleva su temperatura de 0º C a Te.
El calor absorbido por el hielo es Q1=mh·Lf+ mh·c·(Te-0)
Calor absorbido por el calorímetro Q2= k·c·(Te-0)
El calor cedido por el agua es Q3=ma·c·(Te-Ta)
Si el calorímetro está perfectamente aislado, no pierde ni gana calor, se cumplirá que
Q1+Q2+ Q3=0
(2)
En la página “calor específico de un sólido”, ya se ha explicado el significado de masa
equivalente k en agua del calorímetro.
Actividades
Medida del equivalente en agua del calorímetro
Introducimos los siguientes datos:
Masa M de agua en gramos en el calorímetro,
Temperatura T0 inicial del calorímetro
Masa m de agua en gramos en una probeta
Temperatura T del agua
Preparo Ing. Luis A. Bertolino
Página 5
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Se pulsa el botón titulado Preparar, los termómetros y las escalas graduadas de
medida del volumen de agua reflejan los datos introducidos.
Si estamos conformes, se pulsa el botón titulado Calcular. La masa m de agua se
vierte en el calorímetro, y en el termómetro podemos leer la temperatura final de
equilibrio Te.
Ejemplo:
Sea M=170 g, T0=92.7 ºC
Sea m=170 g, y T=2.7 ºC
La temperatura de equilibrio es Te=54.2ºC
El equivalente en agua del calorímetro será
Medida del calor de fusión
Introducimos los siguientes datos:
Masa mh de hielo en gramos en el calorímetro,
Temperatura inicial del hielo se fija en 0ºC
Masa ma del agua en gramos
Temperatura Ta del agua
Se pulsa el botón titulado Preparar.
Preparo Ing. Luis A. Bertolino
Página 6
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Si estamos conformes, se pulsa el botón titulado Calcular. El agua se vierte en el
calorímetro, y en su termómetro podemos leer la temperatura final de equilibrio Te.
En el caso de que solamente una parte del hielo se fundiese, la temperatura final sería
Te=0ºC. Se podría extraer el hielo del calorímetro, y pesarlo en una balanza.
Conocida la masa m de hielo se determina el calor de fusión mediante la fórmula (1).
Cuando se produzca esta situación, se incrementa la masa de agua o su temperatura
o ambas cosas a la vez, hasta conseguir que todo el hielo del calorímetro se funda.
Ejemplo:
Hielo: mh=128 g,
Agua, ma=170 g, y Ta=80ºC
Se funde todo el hielo y la temperatura final de equilibrio es Te=9.5 ºC
La masa equivalente en agua del calorímetro la hemos calculada en el apartado
anterior k=57.4 g
Medida del calor de vaporización
Para medir el calor de vaporización se coloca un recipiente metálico con una masa m
de agua sobre un hornillo eléctrico de potencia P.
Sea la temperatura inicial del agua es Ta. A medida que transcurre el tiempo se va
elevando la temperatura del agua, hasta que entra en ebullición a 100 ºC. Anotamos
el tiempo t1.
El agua se evapora, disminuyendo el nivel de agua en el recipiente hasta que toda el
agua se ha convertido en vapor. Anotamos el tiempo t2 que transcurre desde el
comienzo de la ebullición hasta que se consume el agua.
Preparo Ing. Luis A. Bertolino
Página 7
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Tendremos las siguientes relaciones
P·t1=m·c·(100-Ta)
P·t2=m·Lv
donde Lv es el calor de evaporación del agua que trataremos de determinar,
Eliminamos la cantidad desconocida P en el sistema de dos ecuaciones, y
despejamos Lv.
Preparo Ing. Luis A. Bertolino
Página 8
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
La medida del calor latente de evaporación del agua es problemática, en primer lugar,
es difícil determinar el momento en el que el agua entra en ebullición, y el momento
en el que el agua se evapora completamente.
Las pérdidas de calor son importantes (ley de enfriamiento de Newton) ya que la
diferencias de temperatura entre el agua en ebullición y el ambiente es muy grande.
Habría que tener en cuenta también, el calor absorbido por el recipiente, el agua que
se evapora durante el proceso de calentamiento y el agua que se condensa en las
paredes del recipiente.
Si tenemos en cuenta las pérdidas de calor las ecuaciones se escribirían
P·t1=m·c·(100-Ta)+Q1
P·t2=m·Lv+Q2
Q1 es el calor perdido en el proceso de calentamiento del agua desde la temperatura
inicial Ta hasta que entra en ebullición.
Q2 es el calor perdido en el proceso de cambio de fase de líquido a vapor.
Actividades
Para evitar una excesiva complejidad en la simulación de la experiencia, se ha
supuesto que las pérdidas de calor Q1 y Q2 son despreciables.
Como en una experiencia real, solamente una parte de la energía suministrada por el
hornillo eléctrico, sobre el que se pone el recipiente de agua, se emplea en calentarla,
el resto va a la atmósfera. La potencia efectiva empleada en el calentamiento es igual
a la potencia consumida menos una proporción seleccionada aleatoriamente y
comprendida entre el 10% y el 30%.
Se introduce
La potencia del calentador eléctrico en W, actuando en la barra de desplazamiento
titulada Potencia.
Masa m de agua en gramos en el recipiente
Temperatura inicial Ta del agua
Se pulsa el botón titulado Empieza
Se observa como la temperatura del agua se va incrementando con el tiempo hasta
que en el instante t1 el agua empieza a hervir. A partir de ese momento, el agua se va
evaporando a la temperatura constante de 100ºC, empleando un tiempo t2 en dicho
proceso.
Usando los botones titulados Pausa/Continua y Paso se miden los tiempos t1 y t2.
Preparo Ing. Luis A. Bertolino
Página 9
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Ejemplo:
Potencia 1000 W
Masa de agua: m=200 g
Temperatura inicial, y Ta=20ºC
El agua alcanza la temperatura de 100º C en el instante t=78 s.
El agua se ha evaporado completamente en el instante t=604 s
Tenemos que t1=78s y t2=604-78=526 s
La potencia efectiva P del hornillo eléctrico que se ha empleado en calentar y
evaporar el agua es algo menos de 1000 W.
DETERMINACION DEL CALOR ESPECIFICO DE UN SOLIDO
En esta página, se simula una experiencia de laboratorio poco usual, la medida del
calor específico de un cuerpo metálico empleando la ley del enfriamiento de Newton.
Para ello, tenemos que conocer el calor específico de un cuerpo de las misma forma y
dimensiones que tomamos como referencia.
Ley del enfriamiento de Newton
Cuando la diferencia de temperaturas
entre un cuerpo y su medio ambiente no
es demasiado grande, el calor
transferido en la unidad de tiempo hacia
el cuerpo o desde el cuerpo por
conducción, convección y radiación es
aproximadamente proporcional a la
diferencia de temperatura entre el
cuerpo y el medio externo.
Preparo Ing. Luis A. Bertolino
Página 10
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Donde a es el coeficiente de intercambio de calor y S es el área del cuerpo.
Si la temperatura T del cuerpo es mayor que la temperatura del medio ambiente Ta, el
cuerpo pierde una cantidad de calor dQ en el intervalo de tiempo comprendido entre t
y t+dt, disminuyendo su temperatura T en dT.
dQ=-m·c·dT
donde m=r V es la masa del cuerpo (r es la densidad y V es el volumen), y c el calor
específico.
La ecuación que nos da la variación de la temperatura T del cuerpo en función del
tiempo es
o bien,
Integrando esta ecuación con la condición inicial de que en el instante t=0, la
temperatura del cuerpo es T0.
Obtenemos la relación lineal siguiente.
ln(T-Ta)=-k·t +ln(T0-Ta)
Despejando T obtenemos
Medida del calor específico de una sustancia
En la deducción anterior, hemos supuesto que el calor específico c no cambia con la
temperatura, manteniéndose aproximadamente constante en el intervalo de
temperaturas en la que se realiza el experimento.
Si medimos la temperatura del cuerpo durante su enfriamiento a intervalos regulares
de tiempo, y realizamos una representación gráfica de ln(T-Ta) en función de t,
veremos que los puntos se ajustan a una línea recta, de pendiente –k.
Preparo Ing. Luis A. Bertolino
Página 11
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Podemos medir el área S de la muestra, determinar su masa m=r V mediante una
balanza, y a partir de k calculamos el calor específico c.
Pero tenemos una cantidad desconocida, el coeficiente a , que depende de la forma y
el tamaño de la muestra y el contacto entre la muestra y el medio que la rodea. Sin
embargo, para varias sustancias metálicas en el aire, a tiene el mismo valor si las
formas y los tamaños de todas las muestras son idénticas. Así, se puede determinar a
para una sustancia metálica de calor específico conocido y luego, emplear este valor
para determinar el calor específico de otra sustancia metálica de la misma forma y
tamaño.
En la experiencia simulada, la forma de las muestras ensayadas es cúbica de lado d.
El área de las caras de un cubo es S=6d2 y su volumen V=d3. La expresión de la
constante k será ahora
La muestra que nos va a servir de referencia es el Aluminio cuya densidad es
rAl=2700 kg/m3 y calor específico cAl=880 J/(K·kg).
Determinamos en una experiencia el valor de kAl para una muestra de Aluminio de
forma cúbica de lado d.
Determinamos en otra experiencia la el valor de kx de una muestra de otro material,
de densidad rx conocida, de calor específico cx desconocido, que tenga la misma
forma cúbica y del mismo tamaño d.
Como el valor de a es el mismo. El valor del calor específico desconocido cx lo
podemos obtener a partir de la siguiente relación.
Actividades
En primer lugar, tenemos que elegir el Aluminio como sustancia de referencia en el
control selección titulado Material.
Introducimos los siguientes datos:
La temperatura inicial T0 (menor de 100ºC) en el control de edición titulado
Temperatura.
Preparo Ing. Luis A. Bertolino
Página 12
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
El tamaño de la muestra cúbica, la longitud de su lado d en cm, en el control de
edición titulado Dimensión.
Se pulsa en le botón titulado Empieza
La temperatura ambiente se ha fijado en el programa interactivo, Ta=20ºC.
En la parte izquierda, se observa un cubo de aluminio y un termómetro que indica su
temperatura. En la parte derecha del grafico, se observa la evolución de su
temperatura T a lo largo del tiempo t. Se toman medidas de la temperatura cada 50 s.
Estas medidas se guardan en el control área de texto situado a la izquierda del grafico
Se representa en el eje vertical ln (T-T0), y en el eje horizontal el tiempo t en s. Se
representan los datos "experimentales" mediante puntos y la recta que ajusta a estos
datos. Anotamos el valor de la pendiente, kAl, la densidad del Aluminio rAl=2700
kg/m3, y el calor específico del Aluminio cAl=880 J/(K·kg)
Observamos la evolución de su temperatura T en función del tiempo t. Cuando se ha
acabado de tomar los datos, se pulsa en el botón titulado Gráfica. Apuntamos el valor
de la pendiente de la recta kx y el valor de la densidad del material rx. Para obtener el
valor del calor específico de muestra metálica cx aplicamos la fórmula
Ejemplo: Determinar el calor específico del Hierro conocido el calor específico del
Aluminio.
Sustancia de referencia Aluminio
Temperatura inicial T0=100ºC
Tamaño de la muestra d=10 cm
Valor de la pendiente kAl=0.00530
Densidad rAl=2700 kg/m3
Calor específico cAl=880 Jl/(K·kg)
Sustancia Hierro
Temperatura inicial T0=100ºC
Tamaño de la muestra d=10 cm
Valor de la pendiente kx=0.00355
Preparo Ing. Luis A. Bertolino
Página 13
13/11/2015Fecha de creación
DEPARTAMENTO DE FISICA
CATEDRA DE TERMODINAMICA
DETERMINACION DEL CALOR ESPECÍFICO
Densidad rx=7880 kg/m3.
El calor específico del Hierro es
Preparo Ing. Luis A. Bertolino
Página 14
13/11/2015Fecha de creación