Respuestas final del 7 de dic 2009

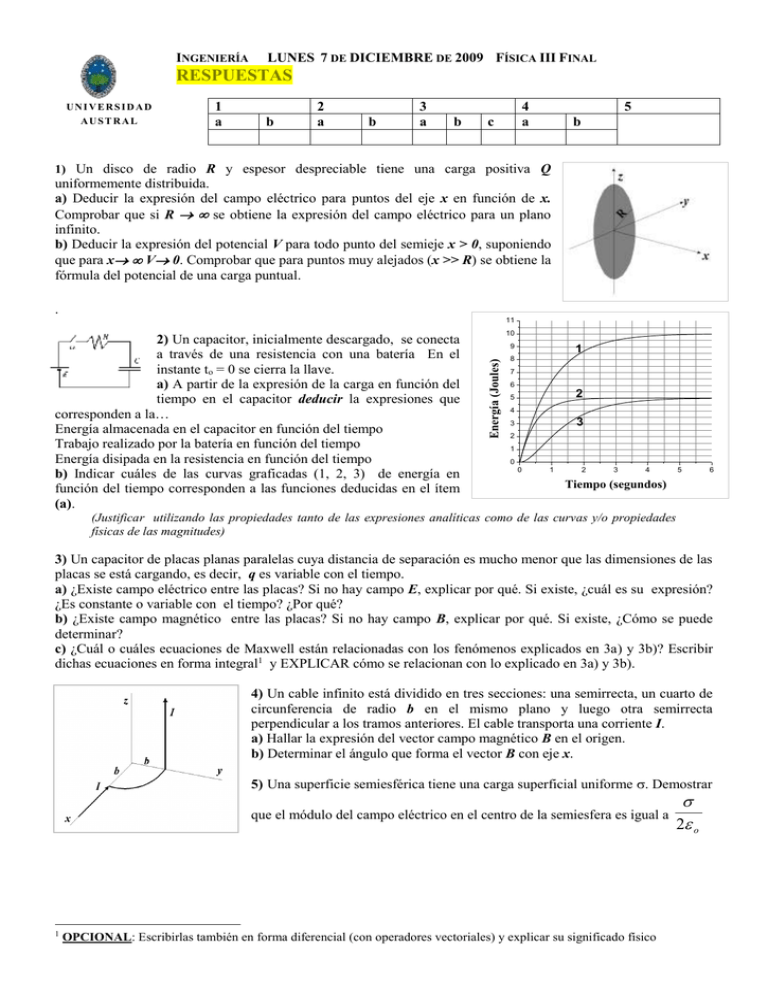
INGENIERÍA
LUNES 7 DE DICIEMBRE DE 2009 FÍSICA III FINAL
RESPUESTAS
UNIVERSIDAD
AUSTRAL
1
a
b
2
a
b
3
a
b
4
a
c
5
b
1) Un disco de radio R y espesor despreciable tiene una carga positiva Q
uniformemente distribuida.
a) Deducir la expresión del campo eléctrico para puntos del eje x en función de x.
Comprobar que si R   se obtiene la expresión del campo eléctrico para un plano
infinito.
b) Deducir la expresión del potencial V para todo punto del semieje x > 0, suponiendo
que para x  V 0. Comprobar que para puntos muy alejados (x >> R) se obtiene la
fórmula del potencial de una carga puntual.
.
11
10
9
Energía (Joules)
2) Un capacitor, inicialmente descargado, se conecta
a través de una resistencia con una batería En el
instante to = 0 se cierra la llave.
a) A partir de la expresión de la carga en función del
tiempo en el capacitor deducir la expresiones que
corresponden a la…
Energía almacenada en el capacitor en función del tiempo
Trabajo realizado por la batería en función del tiempo
Energía disipada en la resistencia en función del tiempo
b) Indicar cuáles de las curvas graficadas (1, 2, 3) de energía en
función del tiempo corresponden a las funciones deducidas en el ítem
(a).
1
8
7
6
2
5
4
3
3
2
1
0
0
1
2
3
4
5
6
Tiempo (segundos)
(Justificar utilizando las propiedades tanto de las expresiones analíticas como de las curvas y/o propiedades
físicas de las magnitudes)
3) Un capacitor de placas planas paralelas cuya distancia de separación es mucho menor que las dimensiones de las
placas se está cargando, es decir, q es variable con el tiempo.
a) ¿Existe campo eléctrico entre las placas? Si no hay campo E, explicar por qué. Si existe, ¿cuál es su expresión?
¿Es constante o variable con el tiempo? ¿Por qué?
b) ¿Existe campo magnético entre las placas? Si no hay campo B, explicar por qué. Si existe, ¿Cómo se puede
determinar?
c) ¿Cuál o cuáles ecuaciones de Maxwell están relacionadas con los fenómenos explicados en 3a) y 3b)? Escribir
dichas ecuaciones en forma integral1 y EXPLICAR cómo se relacionan con lo explicado en 3a) y 3b).
4) Un cable infinito está dividido en tres secciones: una semirrecta, un cuarto de
circunferencia de radio b en el mismo plano y luego otra semirrecta
perpendicular a los tramos anteriores. El cable transporta una corriente I.
a) Hallar la expresión del vector campo magnético B en el origen.
b) Determinar el ángulo que forma el vector B con eje x.
5) Una superficie semiesférica tiene una carga superficial uniforme . Demostrar
que el módulo del campo eléctrico en el centro de la semiesfera es igual a
1
OPCIONAL: Escribirlas también en forma diferencial (con operadores vectoriales) y explicar su significado físico

2 o

1) a) E 

2 o
x
 
x



x
 iˆ    sg ( x) 


2 o 
x2  R2 
x2  R2
 
x
0
E
sg ( x) iˆ
2
2
2

x R
o
Para R
1) b) V


2 o
x
2
x

 R2  x 

2 o
2


R
x 1     1


x


2
u2
1 u 1
2
2
Si u < < 1

 iˆ


1R
R
1   1  
2 x 
x
Si x > > R
2
 1 R 2   R 2
1 Q
Entonces V 
x


2
2 o 2 x
4 o  x 4 o x
2) a)
U cap
t


1
 C 2 1  e 
2





2
t
 

W BAT  C 2 1  e  


2t


1
E R (calor)  C 2 1  e 
2





2)b) Para t > >  , U1/2C2 (asíntota horizontal)
Para t <<, U es una función cuadrática de t.
La pendiente en el origen de U(t) es nula  CURVA 3
Para t > >  , WC2 (asíntota horizontal = doble que para U)
Para t <<, W es una función lineal de t.
Pendiente en el origen 2/R = C2/RC = asíntota/   CURVA 1
Para t > >  , ER1/2C2 (asíntota horizontal) (la misma que para U)
Para t <<, ER es una función lineal de t.
Pendiente en el origen 2/R  CURVA 2
3) a) Hay cargas en las placas  hay campo E entre las placas.
superposición. Como q = q(t)

 = (t)

 
Se puede obtener por la ley de Gauss y por
E 
o
E = E(t)
b) Por la ley de Ampere (o Biot-Savart) hay campo B alrededor del cable que transporta as cargas hacia las placas.
Si hay campo B la integral curvilínea de B en una curva cerrada será proporcional a la corriente que atraviese a
cualquier superficie limitada por dicha curva cerrada. Si tomamos una superficie que pase entre las placas del
capacitor, vemos que no es atravesada por cargas. ¿Entonces? Maxwell propuso que a la ley de Ampere había que
agregarle un término llamado “corriente de desplazamiento” que a pesar de su nombre no corresponde a un
transporte de cargas si no a un campo E variable. Dicha corriente de desplazamiento es proporcional a la derivada
con respecto al tiempo del E entre las placas del capacitor.
c)


 B  dl  
o

 

 i   o  E  dS  Entre las placas del capacitor i = 0, entonces
t




 B  dl   
o
o

 
E  dS

t
Si tomamos un camino circular de perímetro 2r que limita una superficie r2 dentro del espacio entre las placas. El
círculo es paralelo a las placas. Es decir es atraviesa perpendicularmente por las líneas de campo E. Consideramos
que el E es uniforme en el espacio entre placas pero variable en el tiempo:
B  2 r   o  o
B
 o dq
2r dt
 

t   o

1  q
2
   r 2   o  o
   r
 o t  A 

A  r2