comparativa ciclos teóricos termodinámicos mep, mec y

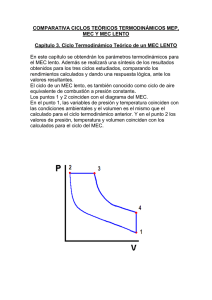
COMPARATIVA CICLOS TEÓRICOS TERMODINÁMICOS MEP,
MEC Y MEC LENTO
Capítulo 2. Ciclo Termodinámico Teórico de un MEC
Los puntos 1 y 2 coinciden con el diagrama del MEP.
En el punto 1, las variables de presión y temperatura coinciden con
las condiciones ambientales y el volumen es el mismo que el
calculado para el ciclo termodinámico anterior. Y en el punto 2 los
valores de presión, temperatura y volumen coinciden con los
calculados para el ciclo del MEP.
Para este ciclo, la presión en la combustión está limitada a 70 bar.
Para los puntos 3, 3A y 4 será necesario el cálculo de los nuevos
parámetros que definen los procesos termodinámicos.
Punto 1. El pistón se encuentra en el PMI, preparado para realizar
la carrera de compresión, y en dicho instante, los valores de presión
y temperatura son los siguientes:
P1  1bar
T1  30  273  303K
Según la ecuación de Clapeyron o de los gases perfectos aplicada
en el punto 1, se obtiene:
P  v  R  T  P1  v1  R  T1
v1 
R  T1
0.287Kj / Kg  K  303K
 v1 
 0.87m 3 / Kg
2
P1
1 100KN / m
Los valores de presión, temperatura y volumen específicos para el
punto 1 quedan de la siguiente forma.
P1
1bar
T1
30ºC
V1 0.87m3/Kg
Punto 2. El pistón ha realizado la carrera de compresión,
desplazándose desde el PMI, hasta el PMS. Durante este proceso
no se cede calor a las paredes el cilindro, por tanto se considera un
proceso adiabático.
Haciendo uso de la ecuación que rige los procesos adiabáticos
entre los puntos 1 y 2, se obtiene la presión, al final de la
compresión.

P1  v1  P2  v2 
 
Cp
Cv
  Relación termodinámica de calores
específicos
Cp  1Kj / Kg  K  Calor específico del aire
como gas ideal, a presión constante.
Cv  0.713Kj / Kg  K  Calor específico del aire
como gas ideal, a volumen constante.
 
Cp
1

 1.4
Cv 0.713
Observando la ecuación de las adiabáticas, para poder obtener P2 ,
es necesario conocer antes v2 .
Rc 
v1
v
0.87
 11  v2  1 
 0.079m 3 / Kg
v2
Rc
11
Aplicamos ahora la ecuación de las adiabáticas y despejamos P2 :

P1  v1  P2  v2 

P2  v1 
    Rc  P2  P1  Rc  1  111.4  28.88bar
P1  v 2 
Para obtener la temperatura, se aplica la ecuación de los gases
perfectos en el punto 2 y se despeja T2
P  v  R  T  P2  v2  R  T2
T2 
P2  v2 2888KN / m 2  0.079m 3 / Kg

 795.48K
R
0.287KJ / KgK
T2  795.48  273  522.5º C
Los parámetros termodinámicos al final de la compresión son los
siguientes:
P2 28.88bar
T2
522.5ºC
V2 0.079m3/Kg
Punto 3. El pistón se encuentra en el PMS y se ha realizado parte
de la combustión a volumen constante. El aporte de calor tiene
lugar mediante un proceso isócoro 2-3.
Del punto 3, conocemos su presión, ya que como se observa en el
diagrama, la presión máxima del ciclo se alcanza en este punto y
debe ser 70 bares. El volumen del punto 3 coincide con el volumen
del punto 2.
Utilizando la ecuación de los gases perfectos, se obtiene la
temperatura en el punto 3.
P  v  R  T  P3  v3  R  T3
T3 
P3  v3 7000KN / m 2  0.079m 3 / Kg
553


 1928K  1655º C
R
0.287KJ / Kg  K
0.287
P3
70bar
T3
1655ºC
V3 0.079m3/Kg
Punto 3A. El pistón comienza su descenso, realizando el final de la
combustión a presión constante. El aporte de calor tiene lugar
mediante un proceso isóbaro 3-3A.
Del punto 3A, conocemos su presión, ya que como se observa en el
diagrama, es la misma que el punto 3.
Para obtener la temperatura y el volumen en el punto 3A, hacemos
uso del balance de calor aportado al ciclo. Dicho calor se aporta
entre 2 y 3A. Los procesos 1-2 y 3A-4 son adiabáticos y el proceso
4-1 representa el calor cedido al foco frío.
El calor aportado al ciclo es dato del problema, por lo que si Cv es
el calor específico a volumen constante, y Cp es el calor específico
a presión constante, se tiene que:
Calor aportado a volumen constante
Qav  Cv  T
T  T3  T2
Qav  Cv  T  Cv  T3  T2 
Calor aportado a presión constante
Qap  Cp  T
T  T3 A  T3
Qap  Cp  T  Cp  T3 A  T3 
Calor total aportado al ciclo
Qa  Cv  T  Cp  T  Cv  (T 3  T 2)  Cp  (T 3A  T 3)
Se despeja T3A
T 3A 
Qa  Cv(T 3  T 2)
2200 0.713 (1928 795.48)
 T3 
 1928 3320.57K  3047.5º C
Cp
1
Conocidas la presión y temperatura, aplicamos la ecuación de los
gases perfectos y se obtiene el volumen específico en dicho punto.
P  v  R  T  P3 A  v3 A  R  T3 A
Se despeja el volumen
v3 A 
R  T3 A 0.287 3320.57

 0.136m 3 / Kg
P3 A
7000
Los parámetros termodinámicos al final de la combustión son los
siguientes:
P3A
70bar
T3A 3047.5ºC
V3A 0.136m3/Kg
Punto 4. Se ha producido la carrera de expansión o trabajo durante
el proceso 3A-4, considerado adiabático porque no existe cesión de
calor. El pistón se encuentra en el PMI a una presión superior a la
atmosférica.
Del punto 4 se puede deducir rapidamente su volumen, ya que debe
coincidir con el volumen del punto 1. El resto de parámetros, como
son la presión y temperatura, se resuelven mediante la ecuación de
las adiabáticas y la ecuación de Clapeyron o de los gases perfectos
respectivamente.
Para calcular las coordenadas del punto 4, tenemos dos datos, la
evolución 3A-4 que es adiabática, por la propia definición del ciclo y
el volumen v4  v1 , así pues;
v4  v1  0.87m3 / Kg
Haciendo uso de la ecuación en el proceso adiabático 3A-4, se
obtiene la presión en el punto 4.

P3 A  v3 A  P4  v4 


v 
P4  v3 A 
 0.136
  P4  P3 A   3 A   70000KN / m 2  
 
 ;
P3 A  v4 
v
0
.
87


 4 
1.4
P4  70000KN / m 2  0.1561.4  5195KN / m 2  5.195bar
Con la ecuación de los gases perfectos aplicada en el punto 4, se
obtiene la temperatura;
P  v  R  T  P4  v4  R  T4
Se despeja la temperatura;
P4  v4 5195KN / m 2  0.87m 3 / Kg
T4 

 1574.16K  1301º C
R
0.287KJ / Kg  K
Las coordenadas del punto cuatro son las siguientes:
P4 5.195bar
T4
1301ºC
V4 0.87m3/Kg
En la siguiente figura se observa el ciclo completo de un MEC lento,
así como los procesos de aporte y cesión de calor.
Una vez obtenidos los valores de presión, temperatura y volumen
específico, en cada uno de los puntos del ciclo y conociendo el calor
aportado por el combustible (que es un dato), se puede aplicar el
primer principio de la termodinámica, para obtener el trabajo
específico;
W  Qa  Qc
W  Trabajo
específico
Qa  Calor aportado
Qc  Calor cedido
El calor aportado es un dato; Qa  2200Kj / Kg
Se calcula ahora el calor cedido en el escape;
Qc  Cv  T  Cv  T4  T1   0.713KJ / KgK  1574.16  303  906.33KJ / kg
El trabajo específico resultante es;
W  Qa  Qc  2200 906.33  1293.67KJ / Kg
El rendimiento termodinámico es;
 tMEC 
Qa  Qc W 1293.67


 0.588
Qa
Qa
2200
Resultados obtenidos para el ciclo teórico de un MEC
MEC
1
2
3
3A
4
P(bar)
1
28.88
70
70
5.195
T(K)
303 795.48 1928 3047.5 1574.16
V(m3/Kg) 0.87 0.079 0.079 0.136
0.87
η=0.588