Teorema de Pitágoras. Teorema de Thales y Semejanza. 1.

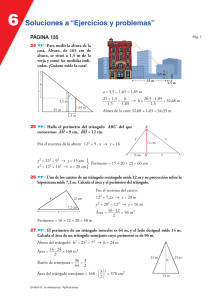
Teorema de Pitágoras. Teorema de Thales y Semejanza.
1.- Se cae un poste de 14,5 m de alto sobre un edificio que se encuentra a 10 m de él.
Cuál es la altura a la que le golpea?
2.- En las fiestas de un pueblo, cuelgan una estrella de 1 m de diámetro en
medio de una cuerda de 34 m que está atada a los extremos de dos postes de
12 m separados 30 m entre sí. ¿A qué altura del suelo queda la estrella?
3.- Sabiendo que las bases de un trapecio isósceles miden 2,4 cm y 5,6 cm, y que la
altura es de 3 cm, calcula la longitud del lado oblicuo.
4.- Calcula la medida de los lados de un rombo cuyas diagonales miden 1 dm y 2,4 dm.
5.- Una maqueta está hecha a escala 1:250. Calcula: a) Las dimensiones de una torre
cilíndrica que en la maqueta mide 6 cm de alturay 4 cm de diámetro.b) La superficie
de un jardín que en la maqueta ocupa 40 cm2.c) El volumen de una piscina que en la
maqueta contiene 20 cm3 de agua.
6.- Un rectángulo tiene unas dimensiones de 10 cm por 15 cm. El lado menor
de otro rectángulo semejante a él mide 12 cm. Halla:
a) La razón de semejanza para pasar del primer al segundo rectángulo.
b)El lado mayor del segundo.
c) Las áreas de ambos rectángulos.
7.- ¿Cuál es la distancia entre el chico y la base de la torre (el chico ve la torre
reflejada en el agua)?
8.- Para determinar que la altura de un eucalipto es de 11 m, Carlos ha medido
la sombra de este (9,6 m) y la suya propia (1,44 m), ambas proyectadas
por el Sol a la misma hora. ¿Cuánto mide Carlos?
9.- ¿Cuál es la altura del siguiente circo?:
10.- ¿Cuánto mide el alto de la estatua del dibujo?
11.- Halla la altura del edificio sabiendo que:
• La mesa tiene 1 m de altura.
12.- La razón de semejanza entre dos triángulos es 2/5. Si el área del mayor es
150 cm2, ¿cuál es el área del menor?
13.- ¿Cuál es la profundidad de un pozo, si su anchura es 1,2 m y alejándote
0,8 m del borde, desde una altura de 1,7 m, ves que la visual une el borde del
pozo con la línea del fondo?
14.- Entre dos pueblos A y B hay una colina. Para medir la distancia AB fijamos
un punto P desde el que se ven los dos pueblos y tomamos las medidas
AP = 15 km, PM = 7,2 km y MN = 12 km. (MN es paralela a AB). Halla la
distancia AB.
15.- El perímetro de un triángulo isósceles es 64 m, y el lado desigual mide
14 m. Calcula el área de un triángulo semejante cuyo perímetro es de 96 m.
16.- Dos triángulos ABC y PQR son semejantes. Los lados del primero miden
24 m, 28 m y 34 m. Calcula la medida de los lados del segundo triángulo
sabiendo que su perímetro es 129 m.
17.- Las áreas de dos triángulos isósceles semejantes son 48 m2 y 108 m2. Si el
lado desigual del primer triángulo es 12 m, ¿cuál es el perímetro del segundo?
18.- De un cono de radio 5 cm hemos cortado otro cono de radio 2 cm y altura 3 cm.
Calcula el volumen del cono grande.
19.- Calcula el volumen de un tronco de pirámide cuadrangular regular en el
que los lados de las bases miden 8 cm y 14 cm y su altura es 15 cm.
20.- En un cono de 10 cm de radio hemos inscrito un cilindro de radio 4 cm y altura
14,4 cm. Halla la altura del cono.
21.- Tenemos un cono inscrito en una esfera de radio 11 cm. ¿Cuál será el radio de la
base del cono si su altura es 14 cm?
22.- Calcula el perímetro del triángulo cuya base coincide con la base mayor de este
trapecio y que se obtiene al prolongar los lados no paralelos hasta que se corten.
23.-Calcula x e y en el siguiente triángulo rectángulo.
24.- Uno de los catetos de un triángulo rectángulo mide 12 m y su proyección
sobre la hipotenusa mide 7,2 m. Calcula el área y el perímetro del triángulo.
25.- Queremos construir un ortoedro de volumen 36 015 cm3 que sea semejante
a otro de dimensiones 25 O 15 O 35 cm. ¿Cuánto medirán sus aristas?