Tema 9. DERIVADAS - Gobierno de Canarias

IES Saulo Torón
Departamento de Matemáticas
Mayores de 25 años. Matemáticas especiales
Tema 9. Derivadas
Tema 9. DERIVADAS
1. Derivada de una función en un punto.
Sea 𝑓(𝑥) una función continua en 𝑥 = 𝑎.
Llamamos derivada de 𝑓(𝑥) en 𝑥 = 𝑎 (la representamos por 𝑓´(𝑎)) al siguiente límite (si
existe y es finito):
𝒇(𝒂 + 𝒉) − 𝒇(𝒂)
𝒉→𝟎
𝒉
𝒇´(𝒂) = 𝐥𝐢𝐦
Si el límite existe, decimos que 𝑓(𝑥) es derivable en 𝑥 = 𝑎. La mayor parte de las funciones
que conocemos son derivables en su dominio.
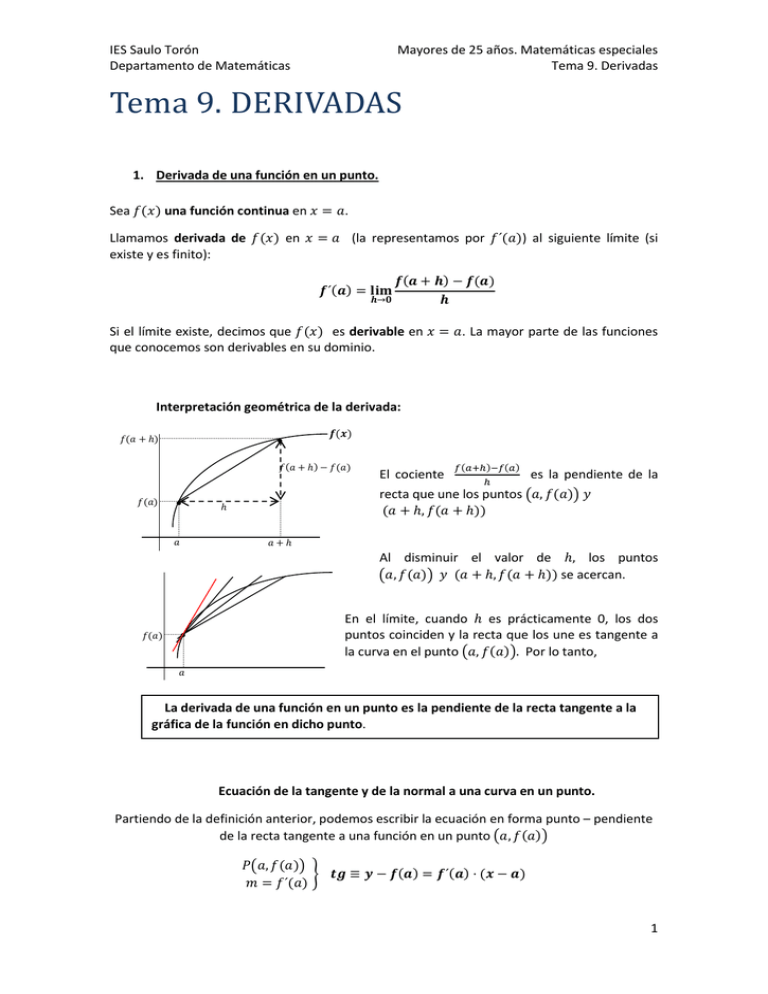
Interpretación geométrica de la derivada:
𝑓(𝑎 + ℎ)
•
𝒇(𝒙)
𝑓(𝑎 + ℎ) − 𝑓(𝑎)
𝑓(𝑎)
•
𝑎
El cociente
𝑓(𝑎+ℎ)−𝑓(𝑎)
ℎ
es la pendiente de la
recta que une los puntos (𝑎, 𝑓(𝑎)) 𝑦
(𝑎 + ℎ, 𝑓(𝑎 + ℎ))
ℎ
𝑎+ℎ
Al disminuir el valor de ℎ, los puntos
(𝑎, 𝑓(𝑎)) 𝑦 (𝑎 + ℎ, 𝑓(𝑎 + ℎ)) se acercan.
𝑓(𝑎)
•
En el límite, cuando ℎ es prácticamente 0, los dos
puntos coinciden y la recta que los une es tangente a
la curva en el punto (𝑎, 𝑓(𝑎)). Por lo tanto,
𝑎
La derivada de una función en un punto es la pendiente de la recta tangente a la
gráfica de la función en dicho punto.
Ecuación de la tangente y de la normal a una curva en un punto.
Partiendo de la definición anterior, podemos escribir la ecuación en forma punto – pendiente
de la recta tangente a una función en un punto (𝑎, 𝑓(𝑎))
𝑃(𝑎, 𝑓(𝑎))
} 𝒕𝒈 ≡ 𝒚 − 𝒇(𝒂) = 𝒇´(𝒂) · (𝒙 − 𝒂)
𝑚 = 𝑓´(𝑎)
1
IES Saulo Torón
Departamento de Matemáticas
Mayores de 25 años. Matemáticas especiales
Tema 9. Derivadas
Del mismo modo, también podemos encontrar la ecuación de la recta normal (la perpendicular
a la tangente) en (𝑎, 𝑓(𝑎)), sabiendo que el producto de las pendientes de dos rectas
perpendiculares es igual a – 1:
𝑃(𝑎, 𝑓(𝑎))
1
1 } 𝒏 ≡ 𝒚 − 𝒇(𝒂) = −
· (𝒙 − 𝒂)
𝑓´(𝑎)
𝑚=−
𝑓´(𝑎)
Derivadas laterales:
Como la derivada de una función en un punto es un límite, sólo existirá si los límites laterales
son finitos e iguales. Definimos las derivadas laterales de la siguiente manera:
𝑓´(𝑎+ ) = lim
h 0
f ( a  h)  f ( a )
. Si este límite existe y es finito diremos que 𝑓 es
h
derivable por la derecha en x = a.
𝑓´(𝑎− ) = lim
h 0 
f ( a  h)  f ( a )
. Si este límite existe y es finito diremos que 𝑓 es
h
derivable por la izquierda en x = a.
Para que una función 𝑓 sea derivable en x = a, las derivadas laterales deben ser iguales, es
decir,
𝒇 𝒆𝒔 𝒅𝒆𝒓𝒊𝒗𝒂𝒃𝒍𝒆 𝒆𝒏 𝒙 = 𝒂 ↔ 𝒇´(𝒂− ) = 𝒇´(𝒂+ )
La mayor parte de las funciones que conocemos son derivables en su dominio (recuérdese que
el que la función sea continua en un punto es condición necesaria para que sea derivable en
él). ¿Cuándo una función continua deja de ser derivable?. Hay dos motivos fundamentales:
a) La gráfica tiene en dicho punto una tangente vertical (la pendiente sería 𝑡𝑔 90°, que
3
no está definida). Ej 𝑦 = √𝑥 en x = 0
b) La gráfica de la función presenta un “punto anguloso”, con lo que las derivadas
laterales no coinciden.
Función derivada:
Si una función es derivable, podemos definir la derivada de una función como
𝒇(𝒙 + 𝒉) − 𝒇(𝒙)
𝒉→𝟎
𝒉
𝒇´(𝒙) = 𝐥𝐢𝐦
Ej. La derivada de la función 𝑓(𝑥) = 𝑥 2 sería:
(𝑥 + ℎ)2 − 𝑥 2
𝑓(𝑥 + ℎ) − 𝑓(𝑥)
𝑥 2 + 2𝑥ℎ + ℎ2 − 𝑥 2
= lim
= lim
=
ℎ→0
ℎ→0
ℎ→0
ℎ
ℎ
ℎ
𝑓´(𝑥) = lim
2𝑥ℎ + ℎ2
ℎ(2𝑥 + ℎ)
= lim
= lim (2𝑥 + ℎ) = 2𝑥
ℎ→0
ℎ→0
ℎ→0
ℎ
ℎ
= lim
2
IES Saulo Torón
Departamento de Matemáticas
Mayores de 25 años. Matemáticas especiales
Tema 9. Derivadas
Naturalmente, es poco práctico utilizar la definición cada vez que tenemos que hallar la
derivada de una función. En la inmensa mayoría de los casos, podemos utilizar la tabla de
derivadas y las reglas de derivación.
1. Tabla de derivadas de funciones elementales
Función
Derivada
Constante: 𝑦 = 𝑘
𝑦´ = 0
Identidad: 𝑦 = 𝑥
𝑦´ = 1
Función
Logarítmicas
1
𝑥
1
1
𝑦´ =
= · log 𝑎 𝑒
𝑥 · ln 𝑎 𝑥
𝑦 = ln 𝑥
𝑦´ =
𝑦 = log 𝑎 𝑥
Potenciales:
𝑦 = 𝑥𝑛
𝑦=
Derivada
𝑦´ = 𝑛 · 𝑥 𝑛−1
1
𝑥𝑛
𝑦´ = −
𝑦´ =
Raíz cuadrada: 𝑦 = √𝑥
Trigonométricas
𝑛
𝑥 𝑛+1
1
2√ 𝑥
𝑦 = 𝑠𝑒𝑛 𝑥
𝑦´ = cos 𝑥
𝑦 = cos 𝑥
𝑦´ = −𝑠𝑒𝑛 𝑥
𝑦´ = 1 + 𝑡𝑔2 𝑥 =
𝑦 = 𝑡𝑔 𝑥
Exponenciales
𝑦 = 𝑎𝑥
𝑦´ = 𝑎 𝑥 · ln 𝑎
𝑦 = 𝑎𝑟𝑐 𝑠𝑒𝑛 𝑥
𝑦 = 𝑒𝑥
𝑦´ = 𝑒 𝑥
𝑦 = 𝑎𝑟𝑐 tg 𝑥
𝑦´ =
1
= 𝑠𝑒𝑐 2 𝑥
𝑐𝑜𝑠 2 𝑥
1
√1 − 𝑥 2
1
𝑦´ =
1 + 𝑥2
2. Reglas de derivación:

La derivada de una suma (resta) de funciones es la suma (resta) de las derivadas.
(𝒇 ± 𝒈)´ = 𝒇´ ± 𝒈´
1
3
Ejemplo: 𝑦 = 𝑥 4 + 𝑥 3 − 𝑠𝑒𝑛 𝑥

𝑦´ = 4𝑥 3 − 𝑥 4 − cos 𝑥
La derivada del producto de una constante por una función es igual a la constante por
la derivada de la función. (Las constantes que multiplican o dividen no se derivan)
𝒚=𝒌·𝒇
𝒚´ = 𝒌 · 𝒇´
Ejemplo: 𝑦 = 2𝑥 → 𝑦´ = 2 · 1 = 2
𝒚=
𝒇
𝒌
𝒚´ =
𝑦 = 3𝑥 2 → 𝑦´ = 3 · 2𝑥 = 6𝑥
𝑦=
𝒇´
𝒌
𝑐𝑜𝑠𝑥
5
→ 𝑦´ = −
𝑠𝑒𝑛𝑥
5
Ejercicios
1. Hallar la función derivada de las siguientes funciones:
a) 𝑦 = 3𝑥 − 7
b) 𝑦 = 𝑥 2 − 5𝑥 + 3
c) 𝑦 =
3𝑥−5𝑥 2
2
3
d) 𝑦 = √𝑥 − √𝑥
1
5
e) 𝑦 = 3 𝑥 3 − 3 𝑥 2 + 7𝑥
f)
g)
h)
i)
2𝑥 − 3 · 5𝑥 + 4 · 𝑒 𝑥
𝑦 = 𝑙𝑛𝑥 − 3 · 𝑙𝑜𝑔𝑥
𝑦 = 3(𝑠𝑒𝑛𝑥 + 𝑐𝑜𝑠𝑥)
𝑦 = 2𝑡𝑔𝑥 − 5 cos 𝑥
3
j) 𝑦 = 𝑥 2 − 𝑎𝑟𝑐𝑡𝑔 𝑥
3
IES Saulo Torón
Departamento de Matemáticas

Mayores de 25 años. Matemáticas especiales
Tema 9. Derivadas
La derivada del producto de dos funciones es igual a la derivada del primero por el
segundo sin derivar, más la derivada del segundo por el primero sin derivar.
𝒚 = 𝒇 · 𝒈 → 𝒚´ = 𝒇´ · 𝒈 + 𝒈´ · 𝒇
Ejemplo: 𝑦 = 3𝑥 2 · 𝑐𝑜𝑠𝑥 𝑦´ = 6𝑥 · cos 𝑥 + (−𝑠𝑒𝑛 𝑥) · 3𝑥 2 = 6𝑥 cos 𝑥 − 3𝑥 2 𝑠𝑒𝑛 𝑥
𝑦 = 2𝑥 · 𝑠𝑒𝑛𝑥 · 𝑙𝑛𝑥

𝑦´ = 2 · 𝑠𝑒𝑛𝑥 · 𝑙𝑛𝑥 + 𝑐𝑜𝑠𝑥 · 2𝑥 · 𝑙𝑛𝑥 +
1
· 2𝑥 · 𝑠𝑒𝑛𝑥
𝑥
La derivada de un cociente de dos funciones es igual a la derivada del numerador por
el denominador sin derivar menos la derivada del denominador por el numerador sin
derivar, partido por el cuadrado del denominador.
𝒚=
Ejemplo: 𝑦 =
2𝑥−1
3𝑥
𝑦´ =
2·3𝑥−3·(2𝑥−1)
(3𝑥)2
𝒇
𝒈
=
𝒚´ =
6𝑥−6𝑥+3
9𝑥 2
𝒇´ · 𝒈 − 𝒈´ · 𝒇
𝒈𝟐
3
1
= 9𝑥 2 = 3𝑥 2
Ejercicios
2. Calcular la función derivada de las siguientes funciones:
1)
f (x)  𝑥 2 · 𝑠𝑒𝑛 𝑥
2) 𝑓(𝑥) =
3)
x
7)𝑓(𝑥) =
x cos x
arcsenx
xarctgx
f ( x)  x 3 ln x
8)𝑓(𝑥) =
5x  2
4x2 1
1
tgx
x
9)𝑓(𝑥) =
x  ex
x  ex
senx  e x cos x
10) 𝑓(𝑥) =
4) 𝑓(𝑥) =
5) 𝑓(𝑥) = e

6) 𝑓(𝑥) = 4
x
senx  cos x
senx  cos x
La derivada de una función compuesta: regla de la cadena
[𝒇(𝒖(𝒙))]´ = 𝒇´(𝒖(𝒙)) · 𝒖´(𝒙)
Ejemplo:
𝑦 = (𝑥 2 − 1)2 → 𝑦´ = 2 · (𝑥 2 − 1) · 2𝑥 = 4𝑥(𝑥 2 − 1)
𝑦 = 𝑙𝑛(𝑡𝑔𝑥)
→ 𝑦´ =
1
1 + 𝑡𝑔2 𝑥
· (1 + 𝑡𝑔2 𝑥) =
𝑡𝑔𝑥
𝑡𝑔𝑥
4
IES Saulo Torón
Departamento de Matemáticas
Mayores de 25 años. Matemáticas especiales
Tema 9. Derivadas
𝑦 = 𝑎𝑟𝑐 𝑡𝑔(5𝑥 − 3) → 𝑦´ =
1
5
·
5
=
1 + (5𝑥 − 3)2
1 + (5𝑥 − 3)2
Vamos a escribir de nuevo toda la tabla de derivadas, referida a funciones compuestas
Función
Derivada
Ejemplos
Funciones potenciales
Funciones exponenciales
2
𝑦 = 𝑢𝑣
𝑦´ = 𝑣 · 𝑢𝑣−1 · 𝑢´ +
+ 𝑣´ · 𝑢𝑣 · 𝑙𝑛𝑢
𝑦 = (3𝑥)𝑥
2
𝑦´ = 𝑥 2 (3𝑥)𝑥 −1 · 3 +
2
+2𝑥 · (3𝑥)𝑥 · ln(3𝑥)
Funciones logarítmicas
Funciones trigonométricas
5
IES Saulo Torón
Departamento de Matemáticas
Mayores de 25 años. Matemáticas especiales
Tema 9. Derivadas
Ejercicios
3. Calcular la función derivada de las siguientes funciones:
1. 𝑓(𝑥) = (3𝑥 − 5)3
7. 𝑓(𝑥) = 𝑙𝑛
18. 𝑓(𝑥) =
y
16.
2. 𝑓(𝑥) = 𝑠𝑒𝑛(𝑥 2 − 7𝑥 + 2)
𝑥+1
𝑥−1
8. 𝑓(𝑥) = 𝑒 𝑥
𝑥 2 −3
3𝑥−5
1
2 x  13
y  senx  cosx
5
2 −3𝑥+2
3. 𝑓(𝑥) = √2𝑥 3 − 3𝑥
14. 𝑓(𝑥) = √𝑥 4 − 3𝑥 + 6
11. 𝑓(𝑥) = ln(𝑙𝑛𝑥)
13. 𝑓(𝑥) = (4𝑥 3 + 6𝑥)5
y  sen3x  sen 2 3x
y  cos3 x  cos( x 3 )
y  ln (senx)
38. y  x a 2  x 2
Aplicaciones de la derivada
Fundamentalmente, para saber cómo y cuánto varía una función en un punto dado. Conocer
este dato es muy útil en muchos campos, tanto científicos como económicos.
En nuestro caso, vamos a aplicarlas a tres aspectos:



Encontrar la ecuación de la recta tangente a la gráfica de una función en un punto
dado.
Estudiar los intervalos donde la función crece y decrece.
Encontrar los puntos en los que la función presenta un máximo o un mínimo.
6
IES Saulo Torón
Departamento de Matemáticas
Mayores de 25 años. Matemáticas especiales
Tema 9. Derivadas
 La recta tangente una función 𝒇(𝒙) en un punto 𝒙 = 𝒂 es la recta que pasa por
dicho punto y cuya pendiente es la derivada de la función en él. Se calcula mediante la
ecuación:
𝒚 = 𝒇(𝒂) + 𝒇´(𝒂) · (𝒙 − 𝒂)
Para hallar la ecuación de la tangente los pasos que seguimos son los siguientes:
1.
2.
3.
4.
Calculamos f(a) para lo cual sustituimos el valor de x = a en la función.
Derivamos la función para obtener f´(x).
Calculamos 𝒇´(𝒂) para lo cual sustituimos el valor de x = a en la derivada.
Escribimos la ecuación de la tangente.
Ejemplo: Hallar la ecuación de la tangente a la función 𝑓(𝑥) = 𝑥 2 − 3𝑥 + 2 𝑒𝑛 𝑥 = 0
1.
𝑓(0) = 02 − 3 · 0 + 2 = 2
2.
𝑓´(𝑥) = 2𝑥 − 3
3.
𝑓´(0) = 2 · 0 − 3 = −3
4.
𝑦 = 𝑓(0) + 𝑓´(0) · (𝑥 − 0) → 𝒚 = 𝟐 − 𝟑𝒙
Ejercicios: Hallar la ecuación de la tangente a las siguientes funciones en los puntos dados:
FUNCIÓN
PUNTO
FUNCIÓN
PUNTO
1
𝑓(𝑥) = 𝑥 2 − 𝑥 + 5
𝑥=1
7
𝑓(𝑥) = 2𝑥 2 − 5𝑥 + 3
2
𝑓(𝑥) = 2𝑥 3 − 5𝑥
𝑥 = −1
8
𝑓(𝑥) = √2𝑥 + 5
𝑥=1
3
𝑓(𝑥) = 2𝑥 + 3/𝑥
𝑥=1
9
𝑥=3
4
𝑓(𝑥) = 8 − 2𝑥 2
𝑥=2
10
𝑓(𝑥) = √𝑥 2 − 𝑥 − 2
3
𝑓(𝑥) = 3𝑥 2 + 2𝑥 −
𝑥
5
𝑓(𝑥) = (2𝑥 − 3)2
𝑥=2
11
𝑓(𝑥) = √3 − 𝑥 3
𝑥 = −1
6
𝑓(𝑥) = (2 − 5𝑥 − 3𝑥 2 )2
𝑥=0
12
𝑓(𝑥) = (2𝑥 − 3)4
𝑥=1
𝑥=
1
2
𝑥 = −3
 Crecimiento de una función en un punto y un intervalo
Una función y = f(x) es creciente en un punto x = a
si al aumentar el valor de x aumenta el de la
función y al disminuir el valor de x también
disminuye el de la función.
Si una función es creciente en un punto, la
derivada de la función en dicho punto es positiva.
7
IES Saulo Torón
Departamento de Matemáticas
Mayores de 25 años. Matemáticas especiales
Tema 9. Derivadas
Una función y = f(x) es decreciente en un punto x = a
si al aumentar el valor de x disminuye el de la función
y al disminuir el valor de x aumenta el de la función.
Si una función es creciente en un punto, la derivada
de la función en dicho punto es positiva.
Una función es creciente en el intervalo (a, b) si la derivada es positiva en todos los
puntos del intervalo y decreciente si es negativa.
Ejemplos: Estudiar si crecen o decrecen las siguientes funciones en los puntos que se
indican:
a) 𝑓(𝑥) = 𝑥 2 − 𝑥 + 5 𝑒𝑛 𝑥 = −3 𝑦 𝑥 = 1
𝑓´(−3) = 2 · (−3) − 1 = −7 𝒇(𝒙)𝒅𝒆𝒄𝒓𝒆𝒄𝒆 𝒆𝒏 𝒙 = −𝟑
𝑓´(𝑥) = 2𝑥 − 1
{
𝑓´(1) = 2 · 1 − 1 = 1
𝒇(𝒙) 𝒄𝒓𝒆𝒄𝒆 𝒆𝒏 𝒙 = 𝟏
b) 𝑓(𝑥) = √5 − 𝑥 2 𝑒𝑛 𝑥 = −1 𝑦
𝑓´(𝑥) =
−2𝑥
2√5 − 𝑥 2
=
−𝑥
𝑥=1
𝑓´(−1) =
+1
√5 − (−1)2
−1
−1
√3 − 𝑥 2
𝑓´(1) =
=
2
2
√5 − 1
{
=
1
𝒇(𝒙)𝒄𝒓𝒆𝒄𝒆𝒆𝒏 𝒙 = −𝟏
2
𝒇(𝒙) 𝒅𝒆𝒄𝒓𝒆𝒄𝒆𝒆𝒏 𝒙 = 𝟏
Para encontrar los intervalos de crecimiento o decrecimiento de una función seguimos los
siguientes pasos:
1. Obtenemos la derivada de la función.
2. Estudiamos el signo de la función derivada. Para ello, lo más sencillo es saber
representarla. Cuando la gráfica de la derivada está por encima del eje OX, la función
crece y cuando está por debajo del eje OX, decrece.
Máximos y mínimos relativos (extremos de una función).
𝑓(𝑥) presenta un máximo relativo en 𝑥 = 𝑎 si en un entorno de 𝑎
se verifica que 𝑓(𝑎) ≥ 𝑓(𝑥) ∀𝑥 del entorno.
𝑓´ = 0
𝑓´ > 0
𝑓´ < 0
𝑎
La función 𝑓(𝑥) es creciente (𝑓´(𝑥) > 0) 𝑠𝑖 𝑥 < 𝑎 y decreciente
(𝑓´(𝑥) < 0) 𝑠𝑖 𝑥 > 𝑎.
Si 𝑓(𝑥) es derivable en 𝑥 = 𝑎, la condición necesaria (no suficiente)
para la existencia de máximo relativo es 𝒇´(𝒂) = 𝟎
8
IES Saulo Torón
Departamento de Matemáticas
Mayores de 25 años. Matemáticas especiales
Tema 9. Derivadas
𝑓(𝑥) presenta un mínimo relativo en 𝑥 = 𝑎 si en un
entorno de 𝑎 se verifica que 𝑓(𝑎) ≤ 𝑓(𝑥) ∀𝑥 del
entorno.
La función 𝑓(𝑥) es decreciente (𝑓´(𝑥) < 0) 𝑠𝑖 𝑥 < 𝑎
creciente (𝑓´(𝑥) > 0) 𝑠𝑖 𝑥 > 𝑎.
y
𝑓´ > 0
𝑓´ < 0
Si 𝑓(𝑥) es derivable en 𝑥 = 𝑎, la condición necesaria (no
suficiente) para la existencia de mínimo relativo es 𝒇´(𝒂) = 𝟎
𝑓´ = 0
𝑎
𝑳𝒂 𝒄𝒐𝒏𝒅𝒊𝒄𝒊ó𝒏 𝒏𝒆𝒄𝒆𝒔𝒂𝒓𝒊𝒂 (𝒏𝒐 𝒔𝒖𝒇𝒊𝒄𝒊𝒆𝒏𝒕𝒆) 𝒑𝒂𝒓𝒂 𝒍𝒂 𝒆𝒙𝒊𝒔𝒕𝒆𝒏𝒄𝒊𝒂 𝒅𝒆 𝒖𝒏
𝒆𝒙𝒕𝒓𝒆𝒎𝒐 𝒓𝒆𝒍𝒂𝒕𝒊𝒗𝒐 𝒆𝒏 𝒙 = 𝒂 𝒆𝒔 𝒒𝒖𝒆 𝒇´(𝒂) = 𝟎
Ejemplo: Estudiar el crecimiento de la función 𝑓(𝑥) = −𝑥 3 + 3𝑥 2 − 9𝑥 + 1
1. 𝑓´(𝑥) = −3𝑥 2 + 6𝑥 − 9
2. Representamos la parábola 𝑦 = −3𝑥 2 + 6𝑥 − 9 para lo cual resolvemos la ecuación:
−6 + 12
𝑥=
= −1
−6
±
−
4
·
3
·
(−9)
−6
±
12
√36
−6
−3𝑥 2 + 6𝑥 − 9 = 0 → 𝑥 =
=
{
−6 − 12
−6
−6
𝑥=
=3
−6
La parábola es cóncava hacia abajo y su gráfica es:
𝑓´ < 0
𝑓´ > 0
−1
𝑓 𝒅𝒆𝒄𝒓𝒆𝒄𝒆
𝑓´ < 0
3
𝑓 𝒄𝒓𝒆𝒄𝒆
𝑓 𝒅𝒆𝒄𝒓𝒆𝒄𝒆
𝒇(𝒙)𝒄𝒓𝒆𝒄𝒆 𝒆𝒏 𝒆𝒍 𝒊𝒏𝒕𝒆𝒓𝒗𝒂𝒍𝒐 (−𝟏, 𝟑)
𝒇(𝒙)𝒅𝒆𝒄𝒓𝒆𝒄𝒆 𝒆𝒏 (−∞, −𝟏) ∪ (𝟑, +∞)
𝑻𝒊𝒆𝒏𝒆 𝒖𝒏 𝒎í𝒏𝒊𝒎𝒐 𝒓𝒆𝒍𝒂𝒕𝒊𝒗𝒐 𝒆𝒏 𝒙 = −𝟏
𝑻𝒊𝒆𝒏𝒆 𝒖𝒏 𝒎á𝒙𝒊𝒎𝒐 𝒓𝒆𝒍𝒂𝒕𝒊𝒗𝒐 𝒆𝒏 𝒙 = 𝟑
9